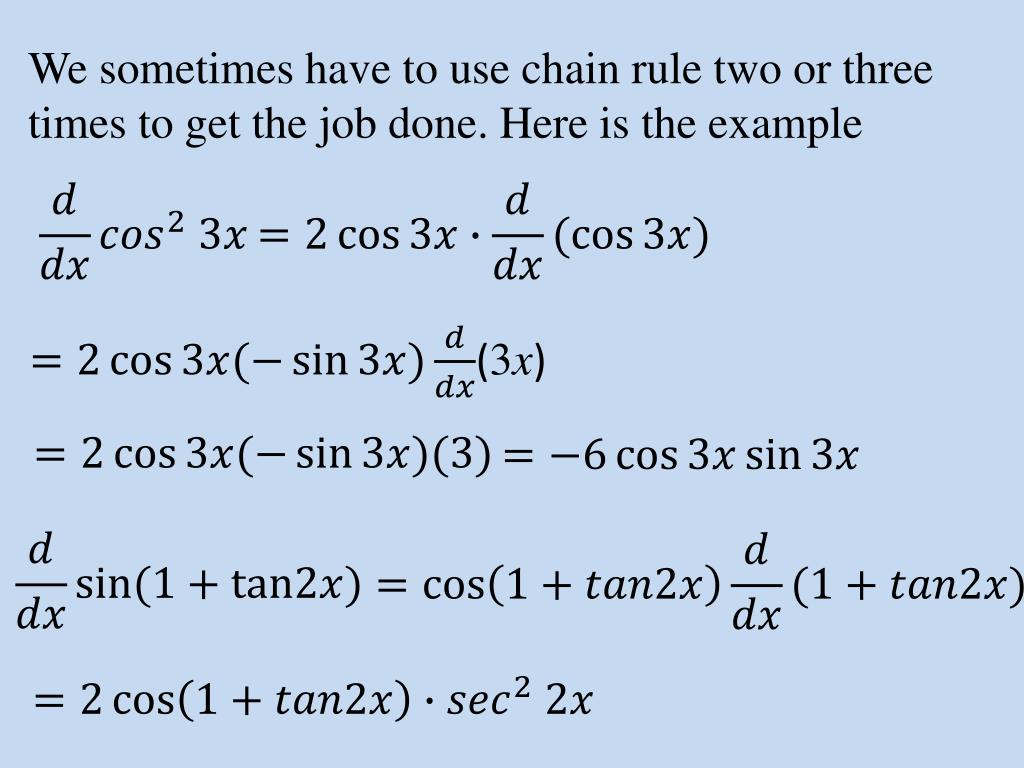Chain Rule Trig Functions Examples . Derivative of a composite function involving trigonometric functiosn. The six basic trigonometric functions include the following: The chain rule is used to differentiate trigonometric functions containing another function. Let’s look at how chain rule works in combination with trigonometric. All derivative rules apply when we differentiate trig functions. We’ve already identified the two. Sine (sin x), cosine (cos x), tangent (tan x), cotangent (cot x), secant (sec x) and cosecant (cosec x). Recognize the chain rule for a composition of three or more functions. Let \ (c (x) = \sin. Describe the proof of the chain rule. The chain rule formula shows us that we must first take the derivative of the outer function keeping the inside function untouched.
from www.slideserve.com
All derivative rules apply when we differentiate trig functions. We’ve already identified the two. The six basic trigonometric functions include the following: The chain rule formula shows us that we must first take the derivative of the outer function keeping the inside function untouched. Recognize the chain rule for a composition of three or more functions. Let \ (c (x) = \sin. Sine (sin x), cosine (cos x), tangent (tan x), cotangent (cot x), secant (sec x) and cosecant (cosec x). The chain rule is used to differentiate trigonometric functions containing another function. Describe the proof of the chain rule. Derivative of a composite function involving trigonometric functiosn.
PPT Aim Chain rules with trigonometric function PowerPoint
Chain Rule Trig Functions Examples All derivative rules apply when we differentiate trig functions. Sine (sin x), cosine (cos x), tangent (tan x), cotangent (cot x), secant (sec x) and cosecant (cosec x). Derivative of a composite function involving trigonometric functiosn. Let \ (c (x) = \sin. The six basic trigonometric functions include the following: Describe the proof of the chain rule. Recognize the chain rule for a composition of three or more functions. We’ve already identified the two. The chain rule is used to differentiate trigonometric functions containing another function. All derivative rules apply when we differentiate trig functions. The chain rule formula shows us that we must first take the derivative of the outer function keeping the inside function untouched. Let’s look at how chain rule works in combination with trigonometric.
From www.youtube.com
Trigonometric Functions and the Chain Rule YouTube Chain Rule Trig Functions Examples Let’s look at how chain rule works in combination with trigonometric. The six basic trigonometric functions include the following: Sine (sin x), cosine (cos x), tangent (tan x), cotangent (cot x), secant (sec x) and cosecant (cosec x). Describe the proof of the chain rule. We’ve already identified the two. All derivative rules apply when we differentiate trig functions. The. Chain Rule Trig Functions Examples.
From www.youtube.com
Derivatives Trig Functions Chain Rule/Double Chain Rule YouTube Chain Rule Trig Functions Examples The chain rule is used to differentiate trigonometric functions containing another function. Let \ (c (x) = \sin. Derivative of a composite function involving trigonometric functiosn. Describe the proof of the chain rule. All derivative rules apply when we differentiate trig functions. The six basic trigonometric functions include the following: Let’s look at how chain rule works in combination with. Chain Rule Trig Functions Examples.
From www.nagwa.com
Question Video Differentiating Trigonometric Functions Using the Chain Chain Rule Trig Functions Examples Describe the proof of the chain rule. Let \ (c (x) = \sin. Sine (sin x), cosine (cos x), tangent (tan x), cotangent (cot x), secant (sec x) and cosecant (cosec x). The chain rule is used to differentiate trigonometric functions containing another function. The six basic trigonometric functions include the following: Let’s look at how chain rule works in. Chain Rule Trig Functions Examples.
From www.youtube.com
Ex Derivatives Using the Chain Rule Involving a Trigonometric Chain Rule Trig Functions Examples We’ve already identified the two. Describe the proof of the chain rule. Recognize the chain rule for a composition of three or more functions. The chain rule formula shows us that we must first take the derivative of the outer function keeping the inside function untouched. All derivative rules apply when we differentiate trig functions. The six basic trigonometric functions. Chain Rule Trig Functions Examples.
From www.scribd.com
Trig Function and Chain Rule Trigonometric Functions Sine Chain Rule Trig Functions Examples Let’s look at how chain rule works in combination with trigonometric. Sine (sin x), cosine (cos x), tangent (tan x), cotangent (cot x), secant (sec x) and cosecant (cosec x). Recognize the chain rule for a composition of three or more functions. The six basic trigonometric functions include the following: The chain rule formula shows us that we must first. Chain Rule Trig Functions Examples.
From www.youtube.com
6 ex3 Triple Chain Rule example of Trig Derivative YouTube Chain Rule Trig Functions Examples Recognize the chain rule for a composition of three or more functions. We’ve already identified the two. All derivative rules apply when we differentiate trig functions. The chain rule formula shows us that we must first take the derivative of the outer function keeping the inside function untouched. The six basic trigonometric functions include the following: Describe the proof of. Chain Rule Trig Functions Examples.
From www.slideserve.com
PPT 2.4 The Chain Rule PowerPoint Presentation, free download ID Chain Rule Trig Functions Examples All derivative rules apply when we differentiate trig functions. The six basic trigonometric functions include the following: Sine (sin x), cosine (cos x), tangent (tan x), cotangent (cot x), secant (sec x) and cosecant (cosec x). Recognize the chain rule for a composition of three or more functions. Describe the proof of the chain rule. Let’s look at how chain. Chain Rule Trig Functions Examples.
From www.kristakingmath.com
Chain rule with trig functions — Krista King Math Online math help Chain Rule Trig Functions Examples Describe the proof of the chain rule. All derivative rules apply when we differentiate trig functions. The six basic trigonometric functions include the following: The chain rule formula shows us that we must first take the derivative of the outer function keeping the inside function untouched. Derivative of a composite function involving trigonometric functiosn. The chain rule is used to. Chain Rule Trig Functions Examples.
From www.youtube.com
chain rule example square root, trig function and power function Chain Rule Trig Functions Examples We’ve already identified the two. The chain rule formula shows us that we must first take the derivative of the outer function keeping the inside function untouched. Derivative of a composite function involving trigonometric functiosn. Sine (sin x), cosine (cos x), tangent (tan x), cotangent (cot x), secant (sec x) and cosecant (cosec x). The six basic trigonometric functions include. Chain Rule Trig Functions Examples.
From www.youtube.com
Ex 5 Determine a Derivatives using The Chain Rule Involving Trig Chain Rule Trig Functions Examples Sine (sin x), cosine (cos x), tangent (tan x), cotangent (cot x), secant (sec x) and cosecant (cosec x). Let’s look at how chain rule works in combination with trigonometric. Recognize the chain rule for a composition of three or more functions. The chain rule formula shows us that we must first take the derivative of the outer function keeping. Chain Rule Trig Functions Examples.
From www.slideserve.com
PPT The Chain Rule for Differentiating Trig Functions PowerPoint Chain Rule Trig Functions Examples Recognize the chain rule for a composition of three or more functions. Sine (sin x), cosine (cos x), tangent (tan x), cotangent (cot x), secant (sec x) and cosecant (cosec x). The chain rule formula shows us that we must first take the derivative of the outer function keeping the inside function untouched. All derivative rules apply when we differentiate. Chain Rule Trig Functions Examples.
From www.youtube.com
Chain Rule with Trig Functions YouTube Chain Rule Trig Functions Examples Let’s look at how chain rule works in combination with trigonometric. All derivative rules apply when we differentiate trig functions. Recognize the chain rule for a composition of three or more functions. The chain rule is used to differentiate trigonometric functions containing another function. Derivative of a composite function involving trigonometric functiosn. Describe the proof of the chain rule. The. Chain Rule Trig Functions Examples.
From www.youtube.com
Chain Rule Part 2 with trig YouTube Chain Rule Trig Functions Examples Sine (sin x), cosine (cos x), tangent (tan x), cotangent (cot x), secant (sec x) and cosecant (cosec x). The six basic trigonometric functions include the following: Describe the proof of the chain rule. We’ve already identified the two. All derivative rules apply when we differentiate trig functions. Derivative of a composite function involving trigonometric functiosn. Recognize the chain rule. Chain Rule Trig Functions Examples.
From www.onlinemathlearning.com
Trigonometric Functions (examples, videos, worksheets, solutions Chain Rule Trig Functions Examples The chain rule formula shows us that we must first take the derivative of the outer function keeping the inside function untouched. Sine (sin x), cosine (cos x), tangent (tan x), cotangent (cot x), secant (sec x) and cosecant (cosec x). All derivative rules apply when we differentiate trig functions. We’ve already identified the two. Recognize the chain rule for. Chain Rule Trig Functions Examples.
From www.slideshare.net
Chain rule & trigonometric functions Chain Rule Trig Functions Examples The chain rule formula shows us that we must first take the derivative of the outer function keeping the inside function untouched. Describe the proof of the chain rule. Recognize the chain rule for a composition of three or more functions. The six basic trigonometric functions include the following: Sine (sin x), cosine (cos x), tangent (tan x), cotangent (cot. Chain Rule Trig Functions Examples.
From mathsathome.com
The Chain Rule Made Easy Examples and Solutions Chain Rule Trig Functions Examples All derivative rules apply when we differentiate trig functions. We’ve already identified the two. Describe the proof of the chain rule. The chain rule is used to differentiate trigonometric functions containing another function. Let’s look at how chain rule works in combination with trigonometric. The chain rule formula shows us that we must first take the derivative of the outer. Chain Rule Trig Functions Examples.
From www.slideshare.net
Chain rule & trigonometric functions Chain Rule Trig Functions Examples Derivative of a composite function involving trigonometric functiosn. Let \ (c (x) = \sin. We’ve already identified the two. The chain rule formula shows us that we must first take the derivative of the outer function keeping the inside function untouched. Let’s look at how chain rule works in combination with trigonometric. Recognize the chain rule for a composition of. Chain Rule Trig Functions Examples.
From www.showme.com
Differentiation of inverse trig functions with Chain Rule Math ShowMe Chain Rule Trig Functions Examples Describe the proof of the chain rule. Sine (sin x), cosine (cos x), tangent (tan x), cotangent (cot x), secant (sec x) and cosecant (cosec x). We’ve already identified the two. The chain rule formula shows us that we must first take the derivative of the outer function keeping the inside function untouched. Recognize the chain rule for a composition. Chain Rule Trig Functions Examples.
From www.youtube.com
Differentiating trigonometric functions using the chain rule Chain Rule Trig Functions Examples Describe the proof of the chain rule. The six basic trigonometric functions include the following: Recognize the chain rule for a composition of three or more functions. We’ve already identified the two. The chain rule is used to differentiate trigonometric functions containing another function. Derivative of a composite function involving trigonometric functiosn. The chain rule formula shows us that we. Chain Rule Trig Functions Examples.
From www.youtube.com
Derivatives Chain Rule with Trig Functions and Exponential Functions Chain Rule Trig Functions Examples Sine (sin x), cosine (cos x), tangent (tan x), cotangent (cot x), secant (sec x) and cosecant (cosec x). The six basic trigonometric functions include the following: The chain rule formula shows us that we must first take the derivative of the outer function keeping the inside function untouched. Describe the proof of the chain rule. Derivative of a composite. Chain Rule Trig Functions Examples.
From www.youtube.com
Trig Derivatives using the Chain Rule YouTube Chain Rule Trig Functions Examples Let \ (c (x) = \sin. All derivative rules apply when we differentiate trig functions. The chain rule formula shows us that we must first take the derivative of the outer function keeping the inside function untouched. Let’s look at how chain rule works in combination with trigonometric. Derivative of a composite function involving trigonometric functiosn. Sine (sin x), cosine. Chain Rule Trig Functions Examples.
From www.teachoo.com
Differentiation Formulas & Rules Basic,Trig Full list Teachoo Chain Rule Trig Functions Examples We’ve already identified the two. Sine (sin x), cosine (cos x), tangent (tan x), cotangent (cot x), secant (sec x) and cosecant (cosec x). Let \ (c (x) = \sin. Derivative of a composite function involving trigonometric functiosn. Let’s look at how chain rule works in combination with trigonometric. All derivative rules apply when we differentiate trig functions. Recognize the. Chain Rule Trig Functions Examples.
From materialmcgheepotshot.z21.web.core.windows.net
Chain Rule On Trig Functions Chain Rule Trig Functions Examples Recognize the chain rule for a composition of three or more functions. We’ve already identified the two. The chain rule formula shows us that we must first take the derivative of the outer function keeping the inside function untouched. The chain rule is used to differentiate trigonometric functions containing another function. Derivative of a composite function involving trigonometric functiosn. The. Chain Rule Trig Functions Examples.
From www.scribd.com
The Chain Rule Trigonometric Functions Derivative Chain Rule Trig Functions Examples Let’s look at how chain rule works in combination with trigonometric. Let \ (c (x) = \sin. The chain rule is used to differentiate trigonometric functions containing another function. All derivative rules apply when we differentiate trig functions. Recognize the chain rule for a composition of three or more functions. We’ve already identified the two. The chain rule formula shows. Chain Rule Trig Functions Examples.
From calcworkshop.com
Trig Derivatives (How To w/ 11+ StepbyStep Examples!) Chain Rule Trig Functions Examples The chain rule formula shows us that we must first take the derivative of the outer function keeping the inside function untouched. Derivative of a composite function involving trigonometric functiosn. We’ve already identified the two. The six basic trigonometric functions include the following: Let \ (c (x) = \sin. Sine (sin x), cosine (cos x), tangent (tan x), cotangent (cot. Chain Rule Trig Functions Examples.
From www.showme.com
Trig chain rule examples Math ShowMe Chain Rule Trig Functions Examples All derivative rules apply when we differentiate trig functions. We’ve already identified the two. The six basic trigonometric functions include the following: Recognize the chain rule for a composition of three or more functions. Describe the proof of the chain rule. The chain rule is used to differentiate trigonometric functions containing another function. Let’s look at how chain rule works. Chain Rule Trig Functions Examples.
From www.slideserve.com
PPT Aim Chain rules with trigonometric function PowerPoint Chain Rule Trig Functions Examples Let’s look at how chain rule works in combination with trigonometric. The chain rule formula shows us that we must first take the derivative of the outer function keeping the inside function untouched. We’ve already identified the two. Describe the proof of the chain rule. All derivative rules apply when we differentiate trig functions. The chain rule is used to. Chain Rule Trig Functions Examples.
From www.youtube.com
Second Derivative with Chain Rule and Trigonometric Function Example Chain Rule Trig Functions Examples All derivative rules apply when we differentiate trig functions. Sine (sin x), cosine (cos x), tangent (tan x), cotangent (cot x), secant (sec x) and cosecant (cosec x). Let \ (c (x) = \sin. Describe the proof of the chain rule. The chain rule is used to differentiate trigonometric functions containing another function. Derivative of a composite function involving trigonometric. Chain Rule Trig Functions Examples.
From mathsathome.com
The Chain Rule Made Easy Examples and Solutions Chain Rule Trig Functions Examples The chain rule formula shows us that we must first take the derivative of the outer function keeping the inside function untouched. The six basic trigonometric functions include the following: Derivative of a composite function involving trigonometric functiosn. All derivative rules apply when we differentiate trig functions. The chain rule is used to differentiate trigonometric functions containing another function. Sine. Chain Rule Trig Functions Examples.
From calcworkshop.com
Chain Rule (Explained w/ 7 StepbyStep Examples!) Chain Rule Trig Functions Examples All derivative rules apply when we differentiate trig functions. The chain rule is used to differentiate trigonometric functions containing another function. The chain rule formula shows us that we must first take the derivative of the outer function keeping the inside function untouched. Let \ (c (x) = \sin. Describe the proof of the chain rule. Recognize the chain rule. Chain Rule Trig Functions Examples.
From www.youtube.com
Ex Derivative Using the Chain Rule Twice Trig Function Raised to Chain Rule Trig Functions Examples Describe the proof of the chain rule. The six basic trigonometric functions include the following: Sine (sin x), cosine (cos x), tangent (tan x), cotangent (cot x), secant (sec x) and cosecant (cosec x). The chain rule is used to differentiate trigonometric functions containing another function. All derivative rules apply when we differentiate trig functions. We’ve already identified the two.. Chain Rule Trig Functions Examples.
From www.slideserve.com
PPT 2.4 The Chain Rule Objective Find the derivative of a composite Chain Rule Trig Functions Examples Let’s look at how chain rule works in combination with trigonometric. The chain rule formula shows us that we must first take the derivative of the outer function keeping the inside function untouched. The six basic trigonometric functions include the following: Sine (sin x), cosine (cos x), tangent (tan x), cotangent (cot x), secant (sec x) and cosecant (cosec x).. Chain Rule Trig Functions Examples.
From www.youtube.com
Example of Chain Rule 3 Trig Functions YouTube Chain Rule Trig Functions Examples Sine (sin x), cosine (cos x), tangent (tan x), cotangent (cot x), secant (sec x) and cosecant (cosec x). The chain rule is used to differentiate trigonometric functions containing another function. Recognize the chain rule for a composition of three or more functions. All derivative rules apply when we differentiate trig functions. Describe the proof of the chain rule. The. Chain Rule Trig Functions Examples.
From www.youtube.com
The Chain Rule with Trig Functions (Calculus 1) YouTube Chain Rule Trig Functions Examples The six basic trigonometric functions include the following: Let’s look at how chain rule works in combination with trigonometric. Sine (sin x), cosine (cos x), tangent (tan x), cotangent (cot x), secant (sec x) and cosecant (cosec x). Let \ (c (x) = \sin. Recognize the chain rule for a composition of three or more functions. The chain rule formula. Chain Rule Trig Functions Examples.
From calcworkshop.com
Trig Derivatives (How To w/ 11+ StepbyStep Examples!) Chain Rule Trig Functions Examples The chain rule is used to differentiate trigonometric functions containing another function. Describe the proof of the chain rule. Sine (sin x), cosine (cos x), tangent (tan x), cotangent (cot x), secant (sec x) and cosecant (cosec x). Recognize the chain rule for a composition of three or more functions. Let’s look at how chain rule works in combination with. Chain Rule Trig Functions Examples.