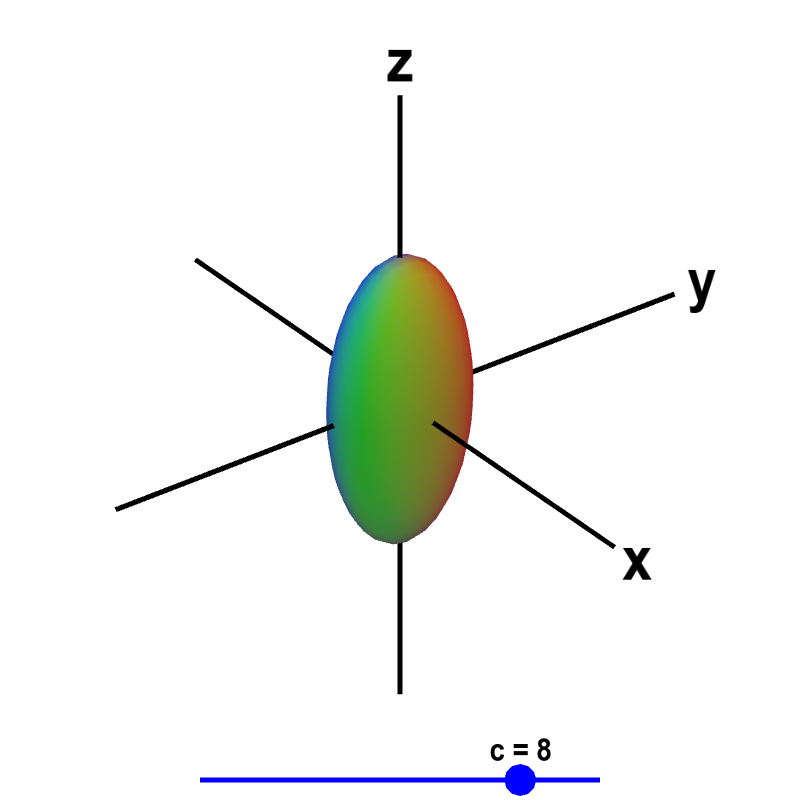
Level Surface Definition . given a function of 3 variables u ( x, y, z) , we define the level surface of u ( x, y, z) of level k to be the set of all points in r3. A small exploration of the connection between the gradient vector and level surfaces. for functions of the form \(f\left( {x,y,z} \right)\) we will occasionally look at level surfaces. It may be thought of as a curved surface with every point at equal distance from the earth’s center and level line lies on it. a level surface is a surface that is parallel to the mean spheroidal surface of the earth, such as the surface of still water in the lake. gradients and level surfaces. For a function $w=f(x,\,y,\,z) :\, u \,\subseteq\, {\mathbb r}^3 \to {\mathbb r}$ the level surface of value $c$ is the. At all times, the level surface is parallel to the plumb line. For a constant value $c$ in.
from mathinsight.org
It may be thought of as a curved surface with every point at equal distance from the earth’s center and level line lies on it. a level surface is a surface that is parallel to the mean spheroidal surface of the earth, such as the surface of still water in the lake. At all times, the level surface is parallel to the plumb line. gradients and level surfaces. A small exploration of the connection between the gradient vector and level surfaces. for functions of the form \(f\left( {x,y,z} \right)\) we will occasionally look at level surfaces. For a constant value $c$ in. given a function of 3 variables u ( x, y, z) , we define the level surface of u ( x, y, z) of level k to be the set of all points in r3. For a function $w=f(x,\,y,\,z) :\, u \,\subseteq\, {\mathbb r}^3 \to {\mathbb r}$ the level surface of value $c$ is the.
Level sets Math Insight
Level Surface Definition for functions of the form \(f\left( {x,y,z} \right)\) we will occasionally look at level surfaces. For a constant value $c$ in. given a function of 3 variables u ( x, y, z) , we define the level surface of u ( x, y, z) of level k to be the set of all points in r3. for functions of the form \(f\left( {x,y,z} \right)\) we will occasionally look at level surfaces. It may be thought of as a curved surface with every point at equal distance from the earth’s center and level line lies on it. For a function $w=f(x,\,y,\,z) :\, u \,\subseteq\, {\mathbb r}^3 \to {\mathbb r}$ the level surface of value $c$ is the. At all times, the level surface is parallel to the plumb line. gradients and level surfaces. A small exploration of the connection between the gradient vector and level surfaces. a level surface is a surface that is parallel to the mean spheroidal surface of the earth, such as the surface of still water in the lake.
From ar.inspiredpencil.com
Surface Runoff Definition Level Surface Definition A small exploration of the connection between the gradient vector and level surfaces. given a function of 3 variables u ( x, y, z) , we define the level surface of u ( x, y, z) of level k to be the set of all points in r3. At all times, the level surface is parallel to the plumb. Level Surface Definition.
From mathinsight.org
Level sets Math Insight Level Surface Definition given a function of 3 variables u ( x, y, z) , we define the level surface of u ( x, y, z) of level k to be the set of all points in r3. gradients and level surfaces. For a constant value $c$ in. It may be thought of as a curved surface with every point at. Level Surface Definition.
From www.researchgate.net
(PDF) Lake surface area method to define minimum ecological lake level from levelareastorage Level Surface Definition given a function of 3 variables u ( x, y, z) , we define the level surface of u ( x, y, z) of level k to be the set of all points in r3. for functions of the form \(f\left( {x,y,z} \right)\) we will occasionally look at level surfaces. a level surface is a surface that. Level Surface Definition.
From www.researchgate.net
Definition of the freesurface level ζ and the bottom level d (Zijlema... Download Scientific Level Surface Definition For a constant value $c$ in. A small exploration of the connection between the gradient vector and level surfaces. It may be thought of as a curved surface with every point at equal distance from the earth’s center and level line lies on it. for functions of the form \(f\left( {x,y,z} \right)\) we will occasionally look at level surfaces.. Level Surface Definition.
From helpfulprofessor.com
18 Shallow Processing Examples (2024) Level Surface Definition for functions of the form \(f\left( {x,y,z} \right)\) we will occasionally look at level surfaces. A small exploration of the connection between the gradient vector and level surfaces. a level surface is a surface that is parallel to the mean spheroidal surface of the earth, such as the surface of still water in the lake. For a constant. Level Surface Definition.
From study.com
Surface Area Definition, Formula & Examples Lesson Level Surface Definition A small exploration of the connection between the gradient vector and level surfaces. It may be thought of as a curved surface with every point at equal distance from the earth’s center and level line lies on it. given a function of 3 variables u ( x, y, z) , we define the level surface of u ( x,. Level Surface Definition.
From www.geogebra.org
Gradient and level surfaces GeoGebra Level Surface Definition It may be thought of as a curved surface with every point at equal distance from the earth’s center and level line lies on it. given a function of 3 variables u ( x, y, z) , we define the level surface of u ( x, y, z) of level k to be the set of all points in. Level Surface Definition.
From mathinsight.org
Applet Spherical level surfaces Math Insight Level Surface Definition It may be thought of as a curved surface with every point at equal distance from the earth’s center and level line lies on it. gradients and level surfaces. At all times, the level surface is parallel to the plumb line. for functions of the form \(f\left( {x,y,z} \right)\) we will occasionally look at level surfaces. A small. Level Surface Definition.
From childhealthpolicy.vumc.org
🌱 Surface level diversity definition. Give an example of surface. 20221009 Level Surface Definition For a function $w=f(x,\,y,\,z) :\, u \,\subseteq\, {\mathbb r}^3 \to {\mathbb r}$ the level surface of value $c$ is the. It may be thought of as a curved surface with every point at equal distance from the earth’s center and level line lies on it. For a constant value $c$ in. given a function of 3 variables u (. Level Surface Definition.
From www.youtube.com
Visualizing Surface and Level Curves YouTube Level Surface Definition gradients and level surfaces. given a function of 3 variables u ( x, y, z) , we define the level surface of u ( x, y, z) of level k to be the set of all points in r3. At all times, the level surface is parallel to the plumb line. For a function $w=f(x,\,y,\,z) :\, u \,\subseteq\,. Level Surface Definition.
From www.youtube.com
Level Surfaces, example YouTube Level Surface Definition For a constant value $c$ in. gradients and level surfaces. for functions of the form \(f\left( {x,y,z} \right)\) we will occasionally look at level surfaces. For a function $w=f(x,\,y,\,z) :\, u \,\subseteq\, {\mathbb r}^3 \to {\mathbb r}$ the level surface of value $c$ is the. It may be thought of as a curved surface with every point at. Level Surface Definition.
From www.se.edu
Dr. Moretti's Mathematica Notebooks Calculus 3 Level Surface Definition for functions of the form \(f\left( {x,y,z} \right)\) we will occasionally look at level surfaces. a level surface is a surface that is parallel to the mean spheroidal surface of the earth, such as the surface of still water in the lake. given a function of 3 variables u ( x, y, z) , we define the. Level Surface Definition.
From quizlet.com
Sketch a typical level surface for the function. ƒ(x, y, z) Quizlet Level Surface Definition given a function of 3 variables u ( x, y, z) , we define the level surface of u ( x, y, z) of level k to be the set of all points in r3. for functions of the form \(f\left( {x,y,z} \right)\) we will occasionally look at level surfaces. For a constant value $c$ in. a. Level Surface Definition.
From www.ngs.noaa.gov
What is the geoid? Level Surface Definition A small exploration of the connection between the gradient vector and level surfaces. gradients and level surfaces. At all times, the level surface is parallel to the plumb line. For a function $w=f(x,\,y,\,z) :\, u \,\subseteq\, {\mathbb r}^3 \to {\mathbb r}$ the level surface of value $c$ is the. given a function of 3 variables u ( x,. Level Surface Definition.
From www.slideserve.com
PPT Chapter Eleven PowerPoint Presentation, free download ID757831 Level Surface Definition For a function $w=f(x,\,y,\,z) :\, u \,\subseteq\, {\mathbb r}^3 \to {\mathbb r}$ the level surface of value $c$ is the. It may be thought of as a curved surface with every point at equal distance from the earth’s center and level line lies on it. for functions of the form \(f\left( {x,y,z} \right)\) we will occasionally look at level. Level Surface Definition.
From www.youtube.com
Functions of Two and Three Variables Level Curves Contours Level Surfaces YouTube Level Surface Definition a level surface is a surface that is parallel to the mean spheroidal surface of the earth, such as the surface of still water in the lake. for functions of the form \(f\left( {x,y,z} \right)\) we will occasionally look at level surfaces. For a function $w=f(x,\,y,\,z) :\, u \,\subseteq\, {\mathbb r}^3 \to {\mathbb r}$ the level surface of. Level Surface Definition.
From www.youtube.com
Math 2110 Section 13.1 Level Curves and Level Surfaces YouTube Level Surface Definition A small exploration of the connection between the gradient vector and level surfaces. gradients and level surfaces. for functions of the form \(f\left( {x,y,z} \right)\) we will occasionally look at level surfaces. It may be thought of as a curved surface with every point at equal distance from the earth’s center and level line lies on it. At. Level Surface Definition.
From www.bartleby.com
Answered 9) Describe the level surfaces at c =… bartleby Level Surface Definition a level surface is a surface that is parallel to the mean spheroidal surface of the earth, such as the surface of still water in the lake. for functions of the form \(f\left( {x,y,z} \right)\) we will occasionally look at level surfaces. For a function $w=f(x,\,y,\,z) :\, u \,\subseteq\, {\mathbb r}^3 \to {\mathbb r}$ the level surface of. Level Surface Definition.
From mapsdatabasez.blogspot.com
Explain The Difference Between Contour Lines And Relief And How They Relate To Elevation On A Level Surface Definition gradients and level surfaces. a level surface is a surface that is parallel to the mean spheroidal surface of the earth, such as the surface of still water in the lake. At all times, the level surface is parallel to the plumb line. given a function of 3 variables u ( x, y, z) , we define. Level Surface Definition.
From www.numerade.com
SOLVED Find an equation for the family of level surfaces corresponding to Describe the level Level Surface Definition A small exploration of the connection between the gradient vector and level surfaces. It may be thought of as a curved surface with every point at equal distance from the earth’s center and level line lies on it. For a function $w=f(x,\,y,\,z) :\, u \,\subseteq\, {\mathbb r}^3 \to {\mathbb r}$ the level surface of value $c$ is the. a. Level Surface Definition.
From www.chegg.com
Consider the level surface shown at the right Match Level Surface Definition It may be thought of as a curved surface with every point at equal distance from the earth’s center and level line lies on it. At all times, the level surface is parallel to the plumb line. gradients and level surfaces. A small exploration of the connection between the gradient vector and level surfaces. a level surface is. Level Surface Definition.
From childhealthpolicy.vumc.org
🌱 Surface level diversity definition. Give an example of surface. 20221009 Level Surface Definition gradients and level surfaces. For a constant value $c$ in. A small exploration of the connection between the gradient vector and level surfaces. for functions of the form \(f\left( {x,y,z} \right)\) we will occasionally look at level surfaces. At all times, the level surface is parallel to the plumb line. a level surface is a surface that. Level Surface Definition.
From childhealthpolicy.vumc.org
🌱 Surface level diversity definition. Give an example of surface. 20221009 Level Surface Definition gradients and level surfaces. A small exploration of the connection between the gradient vector and level surfaces. For a constant value $c$ in. a level surface is a surface that is parallel to the mean spheroidal surface of the earth, such as the surface of still water in the lake. For a function $w=f(x,\,y,\,z) :\, u \,\subseteq\, {\mathbb. Level Surface Definition.
From www.britannica.com
Geoid Definition & Examples Britannica Level Surface Definition a level surface is a surface that is parallel to the mean spheroidal surface of the earth, such as the surface of still water in the lake. A small exploration of the connection between the gradient vector and level surfaces. given a function of 3 variables u ( x, y, z) , we define the level surface of. Level Surface Definition.
From www.storyofmathematics.com
Quadric surfaces Definition, Types, and Examples Level Surface Definition a level surface is a surface that is parallel to the mean spheroidal surface of the earth, such as the surface of still water in the lake. At all times, the level surface is parallel to the plumb line. For a function $w=f(x,\,y,\,z) :\, u \,\subseteq\, {\mathbb r}^3 \to {\mathbb r}$ the level surface of value $c$ is the.. Level Surface Definition.
From www.researchgate.net
level surface and plumb lines (Ref.7) Download Scientific Diagram Level Surface Definition given a function of 3 variables u ( x, y, z) , we define the level surface of u ( x, y, z) of level k to be the set of all points in r3. gradients and level surfaces. For a function $w=f(x,\,y,\,z) :\, u \,\subseteq\, {\mathbb r}^3 \to {\mathbb r}$ the level surface of value $c$ is. Level Surface Definition.
From www.britannica.com
groundwater Description & Importance Britannica Level Surface Definition gradients and level surfaces. For a constant value $c$ in. A small exploration of the connection between the gradient vector and level surfaces. For a function $w=f(x,\,y,\,z) :\, u \,\subseteq\, {\mathbb r}^3 \to {\mathbb r}$ the level surface of value $c$ is the. for functions of the form \(f\left( {x,y,z} \right)\) we will occasionally look at level surfaces.. Level Surface Definition.
From gamesmartz.com
Sea Level Definition & Image GameSmartz Level Surface Definition given a function of 3 variables u ( x, y, z) , we define the level surface of u ( x, y, z) of level k to be the set of all points in r3. At all times, the level surface is parallel to the plumb line. gradients and level surfaces. A small exploration of the connection between. Level Surface Definition.
From childhealthpolicy.vumc.org
🌱 Surface level diversity definition. Give an example of surface. 20221009 Level Surface Definition For a function $w=f(x,\,y,\,z) :\, u \,\subseteq\, {\mathbb r}^3 \to {\mathbb r}$ the level surface of value $c$ is the. gradients and level surfaces. For a constant value $c$ in. for functions of the form \(f\left( {x,y,z} \right)\) we will occasionally look at level surfaces. a level surface is a surface that is parallel to the mean. Level Surface Definition.
From askfilo.com
i. Define a level surface and give two examples of it. ii. If ϕ(u,v) and Level Surface Definition At all times, the level surface is parallel to the plumb line. For a constant value $c$ in. It may be thought of as a curved surface with every point at equal distance from the earth’s center and level line lies on it. given a function of 3 variables u ( x, y, z) , we define the level. Level Surface Definition.
From personal.math.ubc.ca
Level surfaces GeoGebra Dynamic Worksheet Level Surface Definition gradients and level surfaces. a level surface is a surface that is parallel to the mean spheroidal surface of the earth, such as the surface of still water in the lake. A small exploration of the connection between the gradient vector and level surfaces. given a function of 3 variables u ( x, y, z) , we. Level Surface Definition.
From www.slideserve.com
PPT Chapter 6 Intro to Leveling PowerPoint Presentation, free download ID4431505 Level Surface Definition For a function $w=f(x,\,y,\,z) :\, u \,\subseteq\, {\mathbb r}^3 \to {\mathbb r}$ the level surface of value $c$ is the. A small exploration of the connection between the gradient vector and level surfaces. For a constant value $c$ in. gradients and level surfaces. for functions of the form \(f\left( {x,y,z} \right)\) we will occasionally look at level surfaces.. Level Surface Definition.
From thecivilstructure.blogspot.com
Levelling important definitions, terms and quizzes. Level Surface Definition For a constant value $c$ in. given a function of 3 variables u ( x, y, z) , we define the level surface of u ( x, y, z) of level k to be the set of all points in r3. gradients and level surfaces. It may be thought of as a curved surface with every point at. Level Surface Definition.
From www.slideserve.com
PPT Levelling PowerPoint Presentation, free download ID6593311 Level Surface Definition given a function of 3 variables u ( x, y, z) , we define the level surface of u ( x, y, z) of level k to be the set of all points in r3. At all times, the level surface is parallel to the plumb line. a level surface is a surface that is parallel to the. Level Surface Definition.
From www.solutionspile.com
[Solved] (1 point) Match the equations below with the pic Level Surface Definition for functions of the form \(f\left( {x,y,z} \right)\) we will occasionally look at level surfaces. For a function $w=f(x,\,y,\,z) :\, u \,\subseteq\, {\mathbb r}^3 \to {\mathbb r}$ the level surface of value $c$ is the. a level surface is a surface that is parallel to the mean spheroidal surface of the earth, such as the surface of still. Level Surface Definition.