One End Of Uniform Rod . a physical pendulum consists of a uniform rod of length d and mass m pivoted at one end. imagine a strong metal rod of uniform density and thickness floating in a weightless environment. I = (1/12) ml 2. (d)1/2 mw 2 l. How do we evaluate the moment of inertia integral: I = ⅓ ml 2. Since the rod rotates on the horizontal surface, the horizontal component of the. In this case, we use; one end of a uniform rod of mass \(m\) makes contact with a smooth vertical wall, the other with a smooth horizontal floor. The moment of inertia can also be expressed using another formula when the axis of the rod goes through the end of the rod. the moment of inertia about one end is \(\frac{1}{3}\)ml 2, but the moment of inertia through the center of mass along its length is. I = ∫ r 2 dm for. moment of inertia of a rod whose axis goes through the centre of the rod, having mass (m) and length (l) is generally expressed as; The pendulum is initially displaced to one side by a.
from www.chegg.com
the moment of inertia about one end is \(\frac{1}{3}\)ml 2, but the moment of inertia through the center of mass along its length is. The moment of inertia can also be expressed using another formula when the axis of the rod goes through the end of the rod. I = (1/12) ml 2. a physical pendulum consists of a uniform rod of length d and mass m pivoted at one end. one end of a uniform rod of mass \(m\) makes contact with a smooth vertical wall, the other with a smooth horizontal floor. (d)1/2 mw 2 l. imagine a strong metal rod of uniform density and thickness floating in a weightless environment. I = ∫ r 2 dm for. Since the rod rotates on the horizontal surface, the horizontal component of the. In this case, we use;
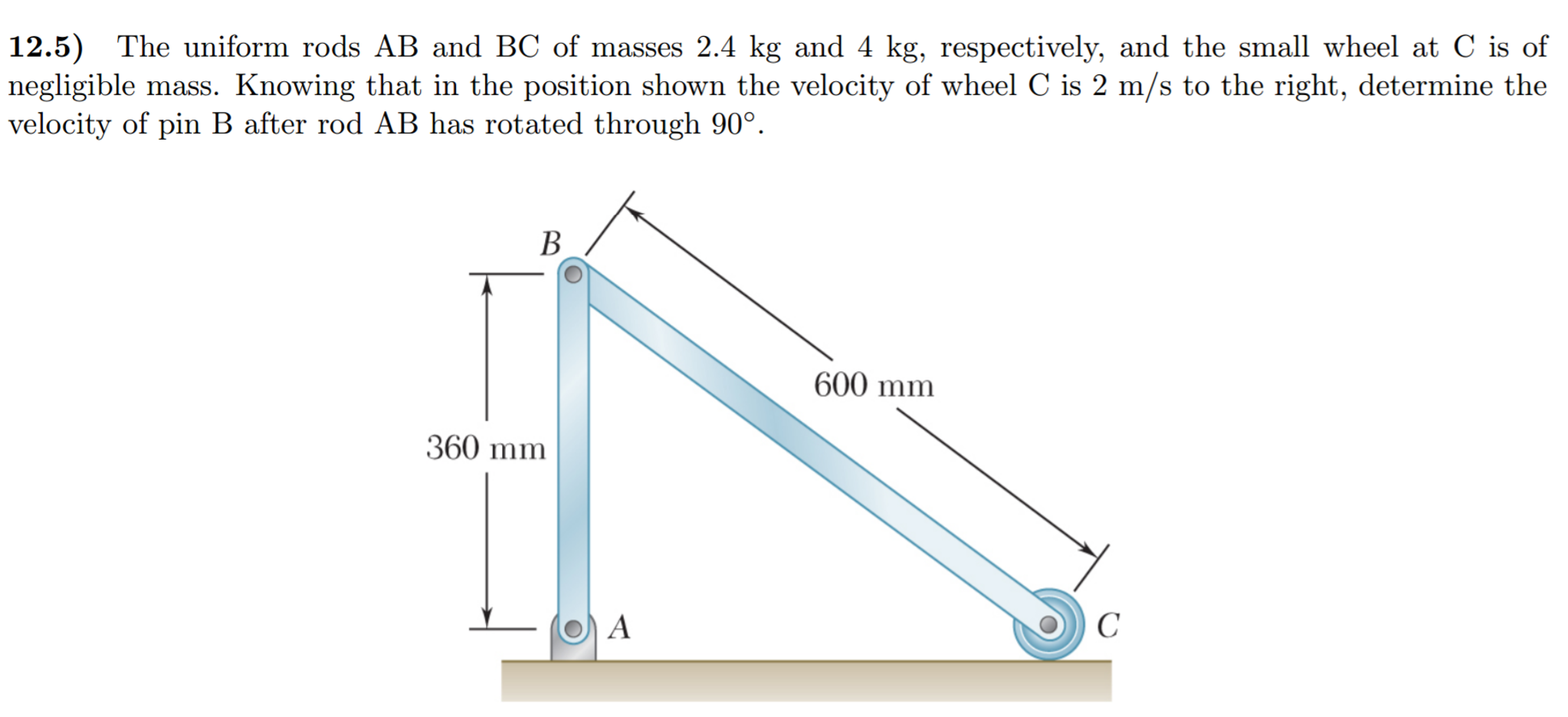
Solved The uniform rods AB and BC of masses 2.4 kg and 4 kg,
One End Of Uniform Rod one end of a uniform rod of mass \(m\) makes contact with a smooth vertical wall, the other with a smooth horizontal floor. The moment of inertia can also be expressed using another formula when the axis of the rod goes through the end of the rod. I = ∫ r 2 dm for. In this case, we use; Since the rod rotates on the horizontal surface, the horizontal component of the. I = ⅓ ml 2. the moment of inertia about one end is \(\frac{1}{3}\)ml 2, but the moment of inertia through the center of mass along its length is. The pendulum is initially displaced to one side by a. How do we evaluate the moment of inertia integral: one end of a uniform rod of mass \(m\) makes contact with a smooth vertical wall, the other with a smooth horizontal floor. imagine a strong metal rod of uniform density and thickness floating in a weightless environment. moment of inertia of a rod whose axis goes through the centre of the rod, having mass (m) and length (l) is generally expressed as; (d)1/2 mw 2 l. a physical pendulum consists of a uniform rod of length d and mass m pivoted at one end. I = (1/12) ml 2.
From www.toppr.com
A long, uniform rod of length L and mass M is pivoted about a One End Of Uniform Rod How do we evaluate the moment of inertia integral: the moment of inertia about one end is \(\frac{1}{3}\)ml 2, but the moment of inertia through the center of mass along its length is. a physical pendulum consists of a uniform rod of length d and mass m pivoted at one end. Since the rod rotates on the horizontal. One End Of Uniform Rod.
From www.toppr.com
One end of a uniform rod having mass m and length l is hinged. The rod One End Of Uniform Rod one end of a uniform rod of mass \(m\) makes contact with a smooth vertical wall, the other with a smooth horizontal floor. (d)1/2 mw 2 l. How do we evaluate the moment of inertia integral: I = ∫ r 2 dm for. In this case, we use; the moment of inertia about one end is \(\frac{1}{3}\)ml. One End Of Uniform Rod.
From www.vrogue.co
The Figure Below Shows A Uniform Rod Of Length L1 1 M vrogue.co One End Of Uniform Rod How do we evaluate the moment of inertia integral: The pendulum is initially displaced to one side by a. I = ⅓ ml 2. the moment of inertia about one end is \(\frac{1}{3}\)ml 2, but the moment of inertia through the center of mass along its length is. (d)1/2 mw 2 l. I = (1/12) ml 2. Since. One End Of Uniform Rod.
From www.chegg.com
Solved The diagram shows a thin rod of uniform mass One End Of Uniform Rod imagine a strong metal rod of uniform density and thickness floating in a weightless environment. How do we evaluate the moment of inertia integral: I = (1/12) ml 2. Since the rod rotates on the horizontal surface, the horizontal component of the. The pendulum is initially displaced to one side by a. I = ∫ r 2 dm for.. One End Of Uniform Rod.
From byjus.com
A thin uniform rod of mass 1 kg and length 0.3 mis smoothly hinged at One End Of Uniform Rod the moment of inertia about one end is \(\frac{1}{3}\)ml 2, but the moment of inertia through the center of mass along its length is. one end of a uniform rod of mass \(m\) makes contact with a smooth vertical wall, the other with a smooth horizontal floor. I = ⅓ ml 2. The pendulum is initially displaced to. One End Of Uniform Rod.
From www.chegg.com
Solved The uniform rods AB and BC of masses 2.4 kg and 4 kg, One End Of Uniform Rod The pendulum is initially displaced to one side by a. one end of a uniform rod of mass \(m\) makes contact with a smooth vertical wall, the other with a smooth horizontal floor. a physical pendulum consists of a uniform rod of length d and mass m pivoted at one end. The moment of inertia can also be. One End Of Uniform Rod.
From byjus.com
A uniform rod is rotated with some angular velocityin horizontal plane One End Of Uniform Rod (d)1/2 mw 2 l. moment of inertia of a rod whose axis goes through the centre of the rod, having mass (m) and length (l) is generally expressed as; one end of a uniform rod of mass \(m\) makes contact with a smooth vertical wall, the other with a smooth horizontal floor. the moment of inertia. One End Of Uniform Rod.
From kunduz.com
[ANSWERED] 37 One end of a uniform rod of length 1 and mass m is hinged One End Of Uniform Rod (d)1/2 mw 2 l. The pendulum is initially displaced to one side by a. a physical pendulum consists of a uniform rod of length d and mass m pivoted at one end. I = ∫ r 2 dm for. I = (1/12) ml 2. I = ⅓ ml 2. moment of inertia of a rod whose axis. One End Of Uniform Rod.
From byjus.com
A uniform rod of mass M and length L is hanging from its one end free One End Of Uniform Rod the moment of inertia about one end is \(\frac{1}{3}\)ml 2, but the moment of inertia through the center of mass along its length is. In this case, we use; Since the rod rotates on the horizontal surface, the horizontal component of the. one end of a uniform rod of mass \(m\) makes contact with a smooth vertical wall,. One End Of Uniform Rod.
From www.youtube.com
ON18 P11 Q11 Weight of Rod Oct/Nov 2018 CAIE A level 9702 Physics One End Of Uniform Rod The moment of inertia can also be expressed using another formula when the axis of the rod goes through the end of the rod. moment of inertia of a rod whose axis goes through the centre of the rod, having mass (m) and length (l) is generally expressed as; the moment of inertia about one end is \(\frac{1}{3}\)ml. One End Of Uniform Rod.
From www.numerade.com
SOLVED Problem A thin, uniform rod of mass M and length L is pivoted One End Of Uniform Rod a physical pendulum consists of a uniform rod of length d and mass m pivoted at one end. The pendulum is initially displaced to one side by a. (d)1/2 mw 2 l. I = ⅓ ml 2. In this case, we use; moment of inertia of a rod whose axis goes through the centre of the rod,. One End Of Uniform Rod.
From www.numerade.com
SOLVED A uniform rod (mass m = 1.0 kg and length L = 2.0 m) pivoted at One End Of Uniform Rod I = ∫ r 2 dm for. one end of a uniform rod of mass \(m\) makes contact with a smooth vertical wall, the other with a smooth horizontal floor. moment of inertia of a rod whose axis goes through the centre of the rod, having mass (m) and length (l) is generally expressed as; (d)1/2 mw. One End Of Uniform Rod.
From www.miniphysics.com
Moment of inertia of a rod (Derivation) Mini Physics Learn Physics One End Of Uniform Rod The moment of inertia can also be expressed using another formula when the axis of the rod goes through the end of the rod. How do we evaluate the moment of inertia integral: Since the rod rotates on the horizontal surface, the horizontal component of the. I = ⅓ ml 2. The pendulum is initially displaced to one side by. One End Of Uniform Rod.
From www.youtube.com
One end of a uniform 4.0mlong rod of weight w is supported by a cable One End Of Uniform Rod I = ⅓ ml 2. The moment of inertia can also be expressed using another formula when the axis of the rod goes through the end of the rod. How do we evaluate the moment of inertia integral: imagine a strong metal rod of uniform density and thickness floating in a weightless environment. I = (1/12) ml 2. I. One End Of Uniform Rod.
From www.doubtnut.com
A uniform thin rod has mass m and length l. One end of the rod lies ov One End Of Uniform Rod The pendulum is initially displaced to one side by a. I = ∫ r 2 dm for. (d)1/2 mw 2 l. How do we evaluate the moment of inertia integral: I = (1/12) ml 2. Since the rod rotates on the horizontal surface, the horizontal component of the. one end of a uniform rod of mass \(m\) makes. One End Of Uniform Rod.
From www.chegg.com
Solved A thin, uniform rod has length L and mass M. A small One End Of Uniform Rod one end of a uniform rod of mass \(m\) makes contact with a smooth vertical wall, the other with a smooth horizontal floor. The moment of inertia can also be expressed using another formula when the axis of the rod goes through the end of the rod. I = ∫ r 2 dm for. In this case, we use;. One End Of Uniform Rod.
From www.doubtnut.com
A uniform rod of weight W is free to rotate about a hinge at one e One End Of Uniform Rod The moment of inertia can also be expressed using another formula when the axis of the rod goes through the end of the rod. I = (1/12) ml 2. How do we evaluate the moment of inertia integral: the moment of inertia about one end is \(\frac{1}{3}\)ml 2, but the moment of inertia through the center of mass along. One End Of Uniform Rod.
From solvedlib.com
A uniform rod of mass M and length L is pivoted about… SolvedLib One End Of Uniform Rod imagine a strong metal rod of uniform density and thickness floating in a weightless environment. the moment of inertia about one end is \(\frac{1}{3}\)ml 2, but the moment of inertia through the center of mass along its length is. I = (1/12) ml 2. Since the rod rotates on the horizontal surface, the horizontal component of the. . One End Of Uniform Rod.
From www.chegg.com
Solved Problem A uniform rod of mass M = 13.0 kg and length One End Of Uniform Rod I = ∫ r 2 dm for. Since the rod rotates on the horizontal surface, the horizontal component of the. the moment of inertia about one end is \(\frac{1}{3}\)ml 2, but the moment of inertia through the center of mass along its length is. imagine a strong metal rod of uniform density and thickness floating in a weightless. One End Of Uniform Rod.
From www.numerade.com
SOLVEDA thin, uniform rod has length L and mass M. A small uniform One End Of Uniform Rod In this case, we use; I = ⅓ ml 2. moment of inertia of a rod whose axis goes through the centre of the rod, having mass (m) and length (l) is generally expressed as; I = ∫ r 2 dm for. one end of a uniform rod of mass \(m\) makes contact with a smooth vertical wall,. One End Of Uniform Rod.
From www.vrogue.co
The Figure Below Shows A Uniform Rod Of Length L1 1 M vrogue.co One End Of Uniform Rod Since the rod rotates on the horizontal surface, the horizontal component of the. moment of inertia of a rod whose axis goes through the centre of the rod, having mass (m) and length (l) is generally expressed as; imagine a strong metal rod of uniform density and thickness floating in a weightless environment. I = (1/12) ml 2.. One End Of Uniform Rod.
From www.chegg.com
Solved One end of a uniform 4.00mlong rod of weight Fg is One End Of Uniform Rod one end of a uniform rod of mass \(m\) makes contact with a smooth vertical wall, the other with a smooth horizontal floor. Since the rod rotates on the horizontal surface, the horizontal component of the. I = (1/12) ml 2. (d)1/2 mw 2 l. I = ⅓ ml 2. moment of inertia of a rod whose. One End Of Uniform Rod.
From www.doubtnut.com
A uniform rod smoothly pivoted at one of its ends is released from res One End Of Uniform Rod The moment of inertia can also be expressed using another formula when the axis of the rod goes through the end of the rod. I = ⅓ ml 2. In this case, we use; the moment of inertia about one end is \(\frac{1}{3}\)ml 2, but the moment of inertia through the center of mass along its length is. How. One End Of Uniform Rod.
From www.doubtnut.com
A uniform rod of length L and mass M is pivoted freely at one end and One End Of Uniform Rod moment of inertia of a rod whose axis goes through the centre of the rod, having mass (m) and length (l) is generally expressed as; the moment of inertia about one end is \(\frac{1}{3}\)ml 2, but the moment of inertia through the center of mass along its length is. I = ⅓ ml 2. The moment of inertia. One End Of Uniform Rod.
From byjus.com
a uniform rod of lengt l and mass m is hinged at one end O and released One End Of Uniform Rod The moment of inertia can also be expressed using another formula when the axis of the rod goes through the end of the rod. In this case, we use; moment of inertia of a rod whose axis goes through the centre of the rod, having mass (m) and length (l) is generally expressed as; Since the rod rotates on. One End Of Uniform Rod.
From www.doubtnut.com
A mass m is at a distance a from one end of a uniform rod of length l One End Of Uniform Rod I = ⅓ ml 2. The pendulum is initially displaced to one side by a. I = (1/12) ml 2. Since the rod rotates on the horizontal surface, the horizontal component of the. I = ∫ r 2 dm for. How do we evaluate the moment of inertia integral: The moment of inertia can also be expressed using another formula. One End Of Uniform Rod.
From www.toppr.com
A uniform rod of mass M and length ℓ is moving on a smooth horizontal One End Of Uniform Rod The moment of inertia can also be expressed using another formula when the axis of the rod goes through the end of the rod. In this case, we use; moment of inertia of a rod whose axis goes through the centre of the rod, having mass (m) and length (l) is generally expressed as; imagine a strong metal. One End Of Uniform Rod.
From www.toppr.com
Toppr Ask Question One End Of Uniform Rod I = ∫ r 2 dm for. The pendulum is initially displaced to one side by a. How do we evaluate the moment of inertia integral: I = (1/12) ml 2. the moment of inertia about one end is \(\frac{1}{3}\)ml 2, but the moment of inertia through the center of mass along its length is. In this case, we. One End Of Uniform Rod.
From askfilo.com
A uniform rod of length L and mass M is hinged at one end and supported b.. One End Of Uniform Rod How do we evaluate the moment of inertia integral: I = ⅓ ml 2. The pendulum is initially displaced to one side by a. Since the rod rotates on the horizontal surface, the horizontal component of the. imagine a strong metal rod of uniform density and thickness floating in a weightless environment. I = (1/12) ml 2. one. One End Of Uniform Rod.
From www.chegg.com
Solved A uniform rod of mass M and length L has a moment of One End Of Uniform Rod (d)1/2 mw 2 l. moment of inertia of a rod whose axis goes through the centre of the rod, having mass (m) and length (l) is generally expressed as; a physical pendulum consists of a uniform rod of length d and mass m pivoted at one end. imagine a strong metal rod of uniform density and. One End Of Uniform Rod.
From www.youtube.com
The Moment of Inertia of a Thin Uniform Rod YouTube One End Of Uniform Rod The moment of inertia can also be expressed using another formula when the axis of the rod goes through the end of the rod. Since the rod rotates on the horizontal surface, the horizontal component of the. a physical pendulum consists of a uniform rod of length d and mass m pivoted at one end. The pendulum is initially. One End Of Uniform Rod.
From www.numerade.com
SOLVED A uniform rod (mass m 3.0 kg and length L = 3.0 m) pivoted at One End Of Uniform Rod one end of a uniform rod of mass \(m\) makes contact with a smooth vertical wall, the other with a smooth horizontal floor. I = ∫ r 2 dm for. I = ⅓ ml 2. the moment of inertia about one end is \(\frac{1}{3}\)ml 2, but the moment of inertia through the center of mass along its length. One End Of Uniform Rod.
From www.chegg.com
Solved The uniform rod has a length l and weight W. It is One End Of Uniform Rod In this case, we use; the moment of inertia about one end is \(\frac{1}{3}\)ml 2, but the moment of inertia through the center of mass along its length is. I = ∫ r 2 dm for. The pendulum is initially displaced to one side by a. I = (1/12) ml 2. moment of inertia of a rod whose. One End Of Uniform Rod.
From www.youtube.com
Torque One end of a uniform 4.0m rod of weight w is supported by a One End Of Uniform Rod the moment of inertia about one end is \(\frac{1}{3}\)ml 2, but the moment of inertia through the center of mass along its length is. imagine a strong metal rod of uniform density and thickness floating in a weightless environment. a physical pendulum consists of a uniform rod of length d and mass m pivoted at one end.. One End Of Uniform Rod.
From www.doubtnut.com
A uniform rod of length L and mass M is pivoted freely at one end and One End Of Uniform Rod I = ⅓ ml 2. The pendulum is initially displaced to one side by a. imagine a strong metal rod of uniform density and thickness floating in a weightless environment. one end of a uniform rod of mass \(m\) makes contact with a smooth vertical wall, the other with a smooth horizontal floor. I = ∫ r 2. One End Of Uniform Rod.