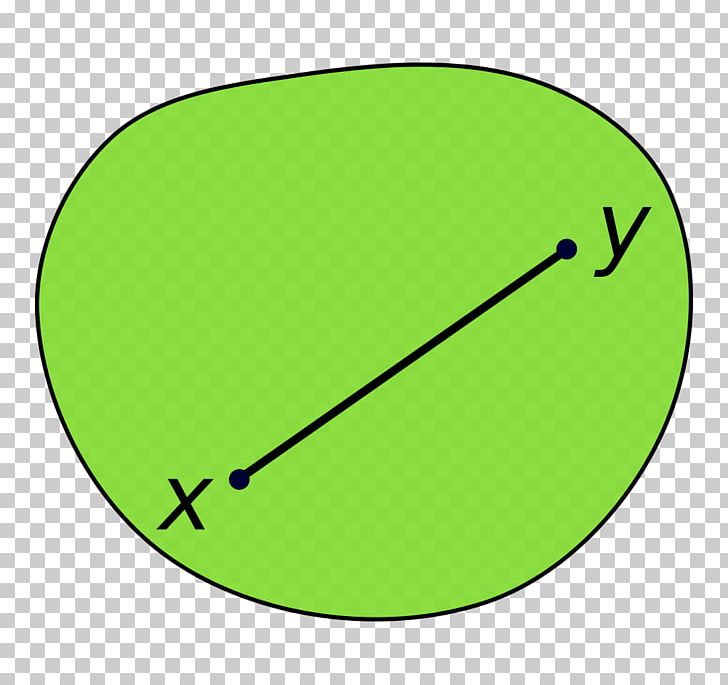
Is A Sphere A Convex Set . I have to show that the unit sphere represented by is convex. A subset u ⊂ s2 u ⊂ s 2 is called convex if. Unfortunately, it's not true that a ball in a metric space is always a convex set (with respect to a linear structure on that metric. I can prove with the triangle inequality that the unit sphere in $r^n$ is convex, but how to show that it is strictly convex? One easy way to show that a set is convex is to construct it from convex sets via convexity preserving operations. Theorem asserts that it is enough to consider convex combinations of m+1 points. In case 2, the theorem of krein and milman asserts that a. Is it true that this domain is convex if and only if all angles of the polygon are in (0, π) (0, π)? Indeed, suppose that x;y 2b(x 0;r), that is, kx x 0 k<r and kx 0 y k<r. Let (l;kk) be a normed linear space. An open sphere b(x 0;r) l is convex.
from imgbin.com
I have to show that the unit sphere represented by is convex. Theorem asserts that it is enough to consider convex combinations of m+1 points. One easy way to show that a set is convex is to construct it from convex sets via convexity preserving operations. I can prove with the triangle inequality that the unit sphere in $r^n$ is convex, but how to show that it is strictly convex? Unfortunately, it's not true that a ball in a metric space is always a convex set (with respect to a linear structure on that metric. Indeed, suppose that x;y 2b(x 0;r), that is, kx x 0 k<r and kx 0 y k<r. Is it true that this domain is convex if and only if all angles of the polygon are in (0, π) (0, π)? Let (l;kk) be a normed linear space. In case 2, the theorem of krein and milman asserts that a. A subset u ⊂ s2 u ⊂ s 2 is called convex if.
Convex Set Convex Function Convex Hull Convex Combination PNG, Clipart, Affine Space, Angle
Is A Sphere A Convex Set Let (l;kk) be a normed linear space. I can prove with the triangle inequality that the unit sphere in $r^n$ is convex, but how to show that it is strictly convex? I have to show that the unit sphere represented by is convex. An open sphere b(x 0;r) l is convex. Unfortunately, it's not true that a ball in a metric space is always a convex set (with respect to a linear structure on that metric. A subset u ⊂ s2 u ⊂ s 2 is called convex if. One easy way to show that a set is convex is to construct it from convex sets via convexity preserving operations. Is it true that this domain is convex if and only if all angles of the polygon are in (0, π) (0, π)? Indeed, suppose that x;y 2b(x 0;r), that is, kx x 0 k<r and kx 0 y k<r. In case 2, the theorem of krein and milman asserts that a. Theorem asserts that it is enough to consider convex combinations of m+1 points. Let (l;kk) be a normed linear space.
From www.slideserve.com
PPT Geometric Optics PowerPoint Presentation, free download ID219116 Is A Sphere A Convex Set A subset u ⊂ s2 u ⊂ s 2 is called convex if. Let (l;kk) be a normed linear space. Is it true that this domain is convex if and only if all angles of the polygon are in (0, π) (0, π)? One easy way to show that a set is convex is to construct it from convex sets. Is A Sphere A Convex Set.
From www.researchgate.net
Demonstrating that a closed ball is a convex set Download Scientific Diagram Is A Sphere A Convex Set Theorem asserts that it is enough to consider convex combinations of m+1 points. One easy way to show that a set is convex is to construct it from convex sets via convexity preserving operations. A subset u ⊂ s2 u ⊂ s 2 is called convex if. I have to show that the unit sphere represented by is convex. Let. Is A Sphere A Convex Set.
From www.youtube.com
LM1.3 Convex Set YouTube Is A Sphere A Convex Set An open sphere b(x 0;r) l is convex. Unfortunately, it's not true that a ball in a metric space is always a convex set (with respect to a linear structure on that metric. Theorem asserts that it is enough to consider convex combinations of m+1 points. I can prove with the triangle inequality that the unit sphere in $r^n$ is. Is A Sphere A Convex Set.
From www.youtube.com
LPP Convex set A Hyperplane is a convex set prove that the sphere is a convex set in Is A Sphere A Convex Set I can prove with the triangle inequality that the unit sphere in $r^n$ is convex, but how to show that it is strictly convex? Unfortunately, it's not true that a ball in a metric space is always a convex set (with respect to a linear structure on that metric. Let (l;kk) be a normed linear space. Indeed, suppose that x;y. Is A Sphere A Convex Set.
From www.semanticscholar.org
Figure 1 from Approximating the Convex Hull for a Set of Spheres Semantic Scholar Is A Sphere A Convex Set One easy way to show that a set is convex is to construct it from convex sets via convexity preserving operations. Let (l;kk) be a normed linear space. In case 2, the theorem of krein and milman asserts that a. Unfortunately, it's not true that a ball in a metric space is always a convex set (with respect to a. Is A Sphere A Convex Set.
From www.cuemath.com
Convex Polygon Definition, Formulas, Properties, Examples Is A Sphere A Convex Set Unfortunately, it's not true that a ball in a metric space is always a convex set (with respect to a linear structure on that metric. Indeed, suppose that x;y 2b(x 0;r), that is, kx x 0 k<r and kx 0 y k<r. A subset u ⊂ s2 u ⊂ s 2 is called convex if. I can prove with the. Is A Sphere A Convex Set.
From imgbin.com
Tetrahedron Geometry Sphere Triangle PNG, Clipart, Angle, Art, Art Paper, Convex Function Is A Sphere A Convex Set An open sphere b(x 0;r) l is convex. I can prove with the triangle inequality that the unit sphere in $r^n$ is convex, but how to show that it is strictly convex? Let (l;kk) be a normed linear space. I have to show that the unit sphere represented by is convex. Theorem asserts that it is enough to consider convex. Is A Sphere A Convex Set.
From www.slideserve.com
PPT Convex Programming PowerPoint Presentation, free download ID1025894 Is A Sphere A Convex Set Theorem asserts that it is enough to consider convex combinations of m+1 points. In case 2, the theorem of krein and milman asserts that a. I can prove with the triangle inequality that the unit sphere in $r^n$ is convex, but how to show that it is strictly convex? Indeed, suppose that x;y 2b(x 0;r), that is, kx x 0. Is A Sphere A Convex Set.
From www.semanticscholar.org
Figure 1 from Convex hulls of spheres and convex hulls of convex polytopes lying on parallel Is A Sphere A Convex Set I have to show that the unit sphere represented by is convex. I can prove with the triangle inequality that the unit sphere in $r^n$ is convex, but how to show that it is strictly convex? Unfortunately, it's not true that a ball in a metric space is always a convex set (with respect to a linear structure on that. Is A Sphere A Convex Set.
From www.slideserve.com
PPT Introduction to Network Mathematics (1) Optimization techniques PowerPoint Presentation Is A Sphere A Convex Set Let (l;kk) be a normed linear space. One easy way to show that a set is convex is to construct it from convex sets via convexity preserving operations. A subset u ⊂ s2 u ⊂ s 2 is called convex if. I have to show that the unit sphere represented by is convex. Is it true that this domain is. Is A Sphere A Convex Set.
From www.slideserve.com
PPT Convex Sets & Concave Sets PowerPoint Presentation, free download ID4828407 Is A Sphere A Convex Set Let (l;kk) be a normed linear space. In case 2, the theorem of krein and milman asserts that a. Indeed, suppose that x;y 2b(x 0;r), that is, kx x 0 k<r and kx 0 y k<r. Theorem asserts that it is enough to consider convex combinations of m+1 points. One easy way to show that a set is convex is. Is A Sphere A Convex Set.
From www.slideserve.com
PPT Convex Sets & Concave Sets PowerPoint Presentation, free download ID480656 Is A Sphere A Convex Set In case 2, the theorem of krein and milman asserts that a. Unfortunately, it's not true that a ball in a metric space is always a convex set (with respect to a linear structure on that metric. Is it true that this domain is convex if and only if all angles of the polygon are in (0, π) (0, π)?. Is A Sphere A Convex Set.
From www.researchgate.net
The convex setin accordance with the constraints (2)of possible... Download Scientific Diagram Is A Sphere A Convex Set I can prove with the triangle inequality that the unit sphere in $r^n$ is convex, but how to show that it is strictly convex? Theorem asserts that it is enough to consider convex combinations of m+1 points. An open sphere b(x 0;r) l is convex. I have to show that the unit sphere represented by is convex. Indeed, suppose that. Is A Sphere A Convex Set.
From www.youtube.com
convex set definition and example PART 2 YouTube Is A Sphere A Convex Set I have to show that the unit sphere represented by is convex. Let (l;kk) be a normed linear space. Is it true that this domain is convex if and only if all angles of the polygon are in (0, π) (0, π)? In case 2, the theorem of krein and milman asserts that a. Unfortunately, it's not true that a. Is A Sphere A Convex Set.
From www.youtube.com
Sum of Convex sets is Convex YouTube Is A Sphere A Convex Set Is it true that this domain is convex if and only if all angles of the polygon are in (0, π) (0, π)? Indeed, suppose that x;y 2b(x 0;r), that is, kx x 0 k<r and kx 0 y k<r. Let (l;kk) be a normed linear space. In case 2, the theorem of krein and milman asserts that a. Unfortunately,. Is A Sphere A Convex Set.
From www.youtube.com
Combinatorial Geometry Part 1 Convex Sets and Convex Hulls YouTube Is A Sphere A Convex Set Let (l;kk) be a normed linear space. An open sphere b(x 0;r) l is convex. Theorem asserts that it is enough to consider convex combinations of m+1 points. Is it true that this domain is convex if and only if all angles of the polygon are in (0, π) (0, π)? In case 2, the theorem of krein and milman. Is A Sphere A Convex Set.
From forums.sketchup.com
Convex part on a sphere without plugins Pro SketchUp Community Is A Sphere A Convex Set An open sphere b(x 0;r) l is convex. I can prove with the triangle inequality that the unit sphere in $r^n$ is convex, but how to show that it is strictly convex? Is it true that this domain is convex if and only if all angles of the polygon are in (0, π) (0, π)? In case 2, the theorem. Is A Sphere A Convex Set.
From www.youtube.com
Convex set & convex combination, intersection of 2 convex set (part2) YouTube Is A Sphere A Convex Set A subset u ⊂ s2 u ⊂ s 2 is called convex if. In case 2, the theorem of krein and milman asserts that a. Theorem asserts that it is enough to consider convex combinations of m+1 points. Indeed, suppose that x;y 2b(x 0;r), that is, kx x 0 k<r and kx 0 y k<r. I have to show that. Is A Sphere A Convex Set.
From imgbin.com
Goldberg Polyhedron Hexagon Konvex Polyeder Sphere PNG, Clipart, Area, Ball, Circle, Convex Set Is A Sphere A Convex Set I have to show that the unit sphere represented by is convex. Let (l;kk) be a normed linear space. One easy way to show that a set is convex is to construct it from convex sets via convexity preserving operations. A subset u ⊂ s2 u ⊂ s 2 is called convex if. I can prove with the triangle inequality. Is A Sphere A Convex Set.
From www.researchgate.net
(PDF) Lecture Notes on Machine Learning Convex Sets Is A Sphere A Convex Set Unfortunately, it's not true that a ball in a metric space is always a convex set (with respect to a linear structure on that metric. In case 2, the theorem of krein and milman asserts that a. A subset u ⊂ s2 u ⊂ s 2 is called convex if. Theorem asserts that it is enough to consider convex combinations. Is A Sphere A Convex Set.
From www.animalia-life.club
Convex And Concave Mirrors And Lenses Is A Sphere A Convex Set One easy way to show that a set is convex is to construct it from convex sets via convexity preserving operations. In case 2, the theorem of krein and milman asserts that a. Unfortunately, it's not true that a ball in a metric space is always a convex set (with respect to a linear structure on that metric. I can. Is A Sphere A Convex Set.
From www.teachoo.com
Principal Focus (and other parts) of Concave and Convex Mirror Is A Sphere A Convex Set One easy way to show that a set is convex is to construct it from convex sets via convexity preserving operations. Let (l;kk) be a normed linear space. An open sphere b(x 0;r) l is convex. Is it true that this domain is convex if and only if all angles of the polygon are in (0, π) (0, π)? Unfortunately,. Is A Sphere A Convex Set.
From machinelearningcoban.com
Machine Learning cơ bản Is A Sphere A Convex Set Theorem asserts that it is enough to consider convex combinations of m+1 points. Unfortunately, it's not true that a ball in a metric space is always a convex set (with respect to a linear structure on that metric. One easy way to show that a set is convex is to construct it from convex sets via convexity preserving operations. Is. Is A Sphere A Convex Set.
From imgbin.com
Geodesic Polyhedron Sphere Geodesic Dome Vertex PNG, Clipart, Ball, Circle, Convex Polytope Is A Sphere A Convex Set In case 2, the theorem of krein and milman asserts that a. Let (l;kk) be a normed linear space. I have to show that the unit sphere represented by is convex. Indeed, suppose that x;y 2b(x 0;r), that is, kx x 0 k<r and kx 0 y k<r. Theorem asserts that it is enough to consider convex combinations of m+1. Is A Sphere A Convex Set.
From www.researchgate.net
Representation of the approximation of the convex set X by the... Download Scientific Diagram Is A Sphere A Convex Set An open sphere b(x 0;r) l is convex. A subset u ⊂ s2 u ⊂ s 2 is called convex if. Is it true that this domain is convex if and only if all angles of the polygon are in (0, π) (0, π)? Indeed, suppose that x;y 2b(x 0;r), that is, kx x 0 k<r and kx 0 y. Is A Sphere A Convex Set.
From machinelearningcoban.com
Machine Learning cơ bản Is A Sphere A Convex Set I can prove with the triangle inequality that the unit sphere in $r^n$ is convex, but how to show that it is strictly convex? Let (l;kk) be a normed linear space. Is it true that this domain is convex if and only if all angles of the polygon are in (0, π) (0, π)? Indeed, suppose that x;y 2b(x 0;r),. Is A Sphere A Convex Set.
From www.techno-science.net
Ensemble convexe Définition et Explications Is A Sphere A Convex Set I can prove with the triangle inequality that the unit sphere in $r^n$ is convex, but how to show that it is strictly convex? Let (l;kk) be a normed linear space. Unfortunately, it's not true that a ball in a metric space is always a convex set (with respect to a linear structure on that metric. Is it true that. Is A Sphere A Convex Set.
From www.semanticscholar.org
Figure 1 from The width of a convex set on the sphere Semantic Scholar Is A Sphere A Convex Set A subset u ⊂ s2 u ⊂ s 2 is called convex if. Theorem asserts that it is enough to consider convex combinations of m+1 points. I can prove with the triangle inequality that the unit sphere in $r^n$ is convex, but how to show that it is strictly convex? An open sphere b(x 0;r) l is convex. One easy. Is A Sphere A Convex Set.
From morioh.com
Visualizing Convex Sets Is A Sphere A Convex Set Indeed, suppose that x;y 2b(x 0;r), that is, kx x 0 k<r and kx 0 y k<r. I have to show that the unit sphere represented by is convex. One easy way to show that a set is convex is to construct it from convex sets via convexity preserving operations. Let (l;kk) be a normed linear space. Theorem asserts that. Is A Sphere A Convex Set.
From machinelearningcoban.com
Machine Learning cơ bản Is A Sphere A Convex Set In case 2, the theorem of krein and milman asserts that a. Theorem asserts that it is enough to consider convex combinations of m+1 points. I can prove with the triangle inequality that the unit sphere in $r^n$ is convex, but how to show that it is strictly convex? A subset u ⊂ s2 u ⊂ s 2 is called. Is A Sphere A Convex Set.
From www.slideserve.com
PPT Lesson 94 PowerPoint Presentation, free download ID520021 Is A Sphere A Convex Set Unfortunately, it's not true that a ball in a metric space is always a convex set (with respect to a linear structure on that metric. Is it true that this domain is convex if and only if all angles of the polygon are in (0, π) (0, π)? An open sphere b(x 0;r) l is convex. One easy way to. Is A Sphere A Convex Set.
From pnghut.com
Light Curved Mirror Sphere Hohlspiegel Convex Set Transparent PNG Is A Sphere A Convex Set Unfortunately, it's not true that a ball in a metric space is always a convex set (with respect to a linear structure on that metric. Let (l;kk) be a normed linear space. In case 2, the theorem of krein and milman asserts that a. One easy way to show that a set is convex is to construct it from convex. Is A Sphere A Convex Set.
From www.youtube.com
Convex Sets Introduction, Definition and Examples YouTube Is A Sphere A Convex Set Is it true that this domain is convex if and only if all angles of the polygon are in (0, π) (0, π)? I can prove with the triangle inequality that the unit sphere in $r^n$ is convex, but how to show that it is strictly convex? A subset u ⊂ s2 u ⊂ s 2 is called convex if.. Is A Sphere A Convex Set.
From imgbin.com
Convex Set Convex Function Convex Hull Convex Combination PNG, Clipart, Affine Space, Angle Is A Sphere A Convex Set I can prove with the triangle inequality that the unit sphere in $r^n$ is convex, but how to show that it is strictly convex? I have to show that the unit sphere represented by is convex. Let (l;kk) be a normed linear space. Theorem asserts that it is enough to consider convex combinations of m+1 points. In case 2, the. Is A Sphere A Convex Set.
From www.slideserve.com
PPT Convexity PowerPoint Presentation, free download ID2514200 Is A Sphere A Convex Set One easy way to show that a set is convex is to construct it from convex sets via convexity preserving operations. Unfortunately, it's not true that a ball in a metric space is always a convex set (with respect to a linear structure on that metric. A subset u ⊂ s2 u ⊂ s 2 is called convex if. I. Is A Sphere A Convex Set.