Geometric Setting Conditions . In the binomial distribution, what do parameters n and p represent? Each observation falls into one of two categories: A geometric setting is a scenario where the outcome of an event is defined by a sequence of independent trials, with each trial having two possible. Two commonly used distributions in statistics are the binomial distribution and the geometric distribution. Geometric settings in a binomial setting, the number of trials n is fixed and the binomial random variable x counts the number of successes. I introduce the geometric setting & distribution in statistics and compare it to the binomial setting. Geometric setting in this chapter we recall some basic notions on points and vectors in rn. 21 rows the geometric setting: What are the four conditions for the binomial setting? The norm of a vector and the scalar product between two. Success or failure (or whatever you wish to call them). ., k and t} is a vector basis of h. The probability of success is the same for each observation.
from www.onlinemathlearning.com
The norm of a vector and the scalar product between two. Success or failure (or whatever you wish to call them). Geometric settings in a binomial setting, the number of trials n is fixed and the binomial random variable x counts the number of successes. In the binomial distribution, what do parameters n and p represent? Two commonly used distributions in statistics are the binomial distribution and the geometric distribution. ., k and t} is a vector basis of h. I introduce the geometric setting & distribution in statistics and compare it to the binomial setting. 21 rows the geometric setting: A geometric setting is a scenario where the outcome of an event is defined by a sequence of independent trials, with each trial having two possible. Each observation falls into one of two categories:
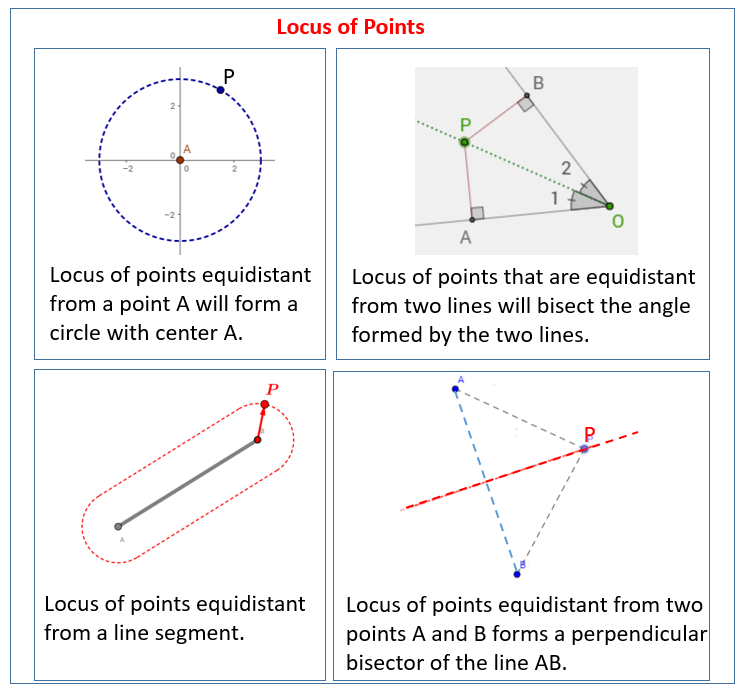
Locus Of A Point (video lessons, diagrams, examples, stepbystep
Geometric Setting Conditions 21 rows the geometric setting: The norm of a vector and the scalar product between two. A geometric setting is a scenario where the outcome of an event is defined by a sequence of independent trials, with each trial having two possible. Each observation falls into one of two categories: What are the four conditions for the binomial setting? Two commonly used distributions in statistics are the binomial distribution and the geometric distribution. 21 rows the geometric setting: I introduce the geometric setting & distribution in statistics and compare it to the binomial setting. Geometric setting in this chapter we recall some basic notions on points and vectors in rn. In the binomial distribution, what do parameters n and p represent? Success or failure (or whatever you wish to call them). The probability of success is the same for each observation. Geometric settings in a binomial setting, the number of trials n is fixed and the binomial random variable x counts the number of successes. ., k and t} is a vector basis of h.
From www.researchgate.net
Illustration of the geometric setting of an instance with its canonical Geometric Setting Conditions Success or failure (or whatever you wish to call them). 21 rows the geometric setting: What are the four conditions for the binomial setting? The probability of success is the same for each observation. Geometric settings in a binomial setting, the number of trials n is fixed and the binomial random variable x counts the number of successes. Each observation. Geometric Setting Conditions.
From www.youtube.com
Geometric distribution existence conditions YouTube Geometric Setting Conditions The probability of success is the same for each observation. Success or failure (or whatever you wish to call them). What are the four conditions for the binomial setting? Geometric settings in a binomial setting, the number of trials n is fixed and the binomial random variable x counts the number of successes. I introduce the geometric setting & distribution. Geometric Setting Conditions.
From www.researchgate.net
Geometric setting for Sections 5 and 6 Download Scientific Diagram Geometric Setting Conditions ., k and t} is a vector basis of h. The probability of success is the same for each observation. What are the four conditions for the binomial setting? The norm of a vector and the scalar product between two. Each observation falls into one of two categories: I introduce the geometric setting & distribution in statistics and compare it. Geometric Setting Conditions.
From www.researchgate.net
Geometric configuration and boundary conditions. Download Scientific Geometric Setting Conditions 21 rows the geometric setting: The probability of success is the same for each observation. In the binomial distribution, what do parameters n and p represent? ., k and t} is a vector basis of h. Geometric settings in a binomial setting, the number of trials n is fixed and the binomial random variable x counts the number of successes.. Geometric Setting Conditions.
From www.researchgate.net
(a) Geometric configuration and boundary conditions of the tested Geometric Setting Conditions I introduce the geometric setting & distribution in statistics and compare it to the binomial setting. Success or failure (or whatever you wish to call them). 21 rows the geometric setting: Two commonly used distributions in statistics are the binomial distribution and the geometric distribution. What are the four conditions for the binomial setting? A geometric setting is a scenario. Geometric Setting Conditions.
From www.researchgate.net
Geometric conditions at image acquisition. Download Scientific Diagram Geometric Setting Conditions The norm of a vector and the scalar product between two. In the binomial distribution, what do parameters n and p represent? I introduce the geometric setting & distribution in statistics and compare it to the binomial setting. 21 rows the geometric setting: Each observation falls into one of two categories: A geometric setting is a scenario where the outcome. Geometric Setting Conditions.
From calcworkshop.com
Geometric Distribution (Explained w/ 5+ Examples!) Geometric Setting Conditions Each observation falls into one of two categories: Two commonly used distributions in statistics are the binomial distribution and the geometric distribution. I introduce the geometric setting & distribution in statistics and compare it to the binomial setting. What are the four conditions for the binomial setting? The norm of a vector and the scalar product between two. A geometric. Geometric Setting Conditions.
From www.slideserve.com
PPT Section 6.3 Binomial and Geometric Random Variables PowerPoint Geometric Setting Conditions A geometric setting is a scenario where the outcome of an event is defined by a sequence of independent trials, with each trial having two possible. Each observation falls into one of two categories: Geometric setting in this chapter we recall some basic notions on points and vectors in rn. I introduce the geometric setting & distribution in statistics and. Geometric Setting Conditions.
From www.numerade.com
SOLVEDGive a geometric description of the set of points in space whose Geometric Setting Conditions What are the four conditions for the binomial setting? Geometric setting in this chapter we recall some basic notions on points and vectors in rn. The norm of a vector and the scalar product between two. ., k and t} is a vector basis of h. In the binomial distribution, what do parameters n and p represent? Each observation falls. Geometric Setting Conditions.
From www.youtube.com
Setting up the Geometry, Mesh, and Boundary Conditions in HyperMesh 11. Geometric Setting Conditions What are the four conditions for the binomial setting? I introduce the geometric setting & distribution in statistics and compare it to the binomial setting. The norm of a vector and the scalar product between two. 21 rows the geometric setting: ., k and t} is a vector basis of h. A geometric setting is a scenario where the outcome. Geometric Setting Conditions.
From www.researchgate.net
Illustration and notation of the geometric setting Download Geometric Setting Conditions I introduce the geometric setting & distribution in statistics and compare it to the binomial setting. A geometric setting is a scenario where the outcome of an event is defined by a sequence of independent trials, with each trial having two possible. What are the four conditions for the binomial setting? ., k and t} is a vector basis of. Geometric Setting Conditions.
From www.doc.pmod.com
Geometric Model Construction and CFD Simulation > CFD Simulation and Geometric Setting Conditions ., k and t} is a vector basis of h. Success or failure (or whatever you wish to call them). Geometric settings in a binomial setting, the number of trials n is fixed and the binomial random variable x counts the number of successes. Geometric setting in this chapter we recall some basic notions on points and vectors in rn.. Geometric Setting Conditions.
From www.slideserve.com
PPT Section 8.2 Geometric Distributions PowerPoint Presentation, free Geometric Setting Conditions What are the four conditions for the binomial setting? ., k and t} is a vector basis of h. Geometric setting in this chapter we recall some basic notions on points and vectors in rn. 21 rows the geometric setting: The probability of success is the same for each observation. Each observation falls into one of two categories: Geometric settings. Geometric Setting Conditions.
From www.researchgate.net
Geometric setting notation of phasefield fracture model Download Geometric Setting Conditions Geometric settings in a binomial setting, the number of trials n is fixed and the binomial random variable x counts the number of successes. What are the four conditions for the binomial setting? I introduce the geometric setting & distribution in statistics and compare it to the binomial setting. Each observation falls into one of two categories: Success or failure. Geometric Setting Conditions.
From www.slideserve.com
PPT Day 2 Review PowerPoint Presentation, free download ID8844614 Geometric Setting Conditions Geometric setting in this chapter we recall some basic notions on points and vectors in rn. 21 rows the geometric setting: Geometric settings in a binomial setting, the number of trials n is fixed and the binomial random variable x counts the number of successes. ., k and t} is a vector basis of h. A geometric setting is a. Geometric Setting Conditions.
From www.researchgate.net
Schematic of the geometric setting of Theorem 7.10. The timelike paths Geometric Setting Conditions 21 rows the geometric setting: A geometric setting is a scenario where the outcome of an event is defined by a sequence of independent trials, with each trial having two possible. The probability of success is the same for each observation. I introduce the geometric setting & distribution in statistics and compare it to the binomial setting. Success or failure. Geometric Setting Conditions.
From www.researchgate.net
Mechanism configuration with different geometric constraint conditions Geometric Setting Conditions 21 rows the geometric setting: The probability of success is the same for each observation. I introduce the geometric setting & distribution in statistics and compare it to the binomial setting. A geometric setting is a scenario where the outcome of an event is defined by a sequence of independent trials, with each trial having two possible. Two commonly used. Geometric Setting Conditions.
From www.slideserve.com
PPT Chapter 8 The Binomial and Geometric Distributions YMS 8.1 Geometric Setting Conditions The probability of success is the same for each observation. Geometric setting in this chapter we recall some basic notions on points and vectors in rn. What are the four conditions for the binomial setting? I introduce the geometric setting & distribution in statistics and compare it to the binomial setting. ., k and t} is a vector basis of. Geometric Setting Conditions.
From www.nagwa.com
Lesson Video Geometric Concepts Nagwa Geometric Setting Conditions ., k and t} is a vector basis of h. The probability of success is the same for each observation. Geometric settings in a binomial setting, the number of trials n is fixed and the binomial random variable x counts the number of successes. The norm of a vector and the scalar product between two. What are the four conditions. Geometric Setting Conditions.
From www.youtube.com
Geometric Setting & Distribution in Statistics YouTube Geometric Setting Conditions Geometric setting in this chapter we recall some basic notions on points and vectors in rn. What are the four conditions for the binomial setting? ., k and t} is a vector basis of h. Geometric settings in a binomial setting, the number of trials n is fixed and the binomial random variable x counts the number of successes. In. Geometric Setting Conditions.
From www.onlinemathlearning.com
Locus Of A Point (video lessons, diagrams, examples, stepbystep Geometric Setting Conditions Geometric settings in a binomial setting, the number of trials n is fixed and the binomial random variable x counts the number of successes. What are the four conditions for the binomial setting? Each observation falls into one of two categories: Two commonly used distributions in statistics are the binomial distribution and the geometric distribution. ., k and t} is. Geometric Setting Conditions.
From www.researchgate.net
Geometric setting with four views and two known triangles. Download Geometric Setting Conditions ., k and t} is a vector basis of h. Success or failure (or whatever you wish to call them). In the binomial distribution, what do parameters n and p represent? Two commonly used distributions in statistics are the binomial distribution and the geometric distribution. The probability of success is the same for each observation. What are the four conditions. Geometric Setting Conditions.
From www.youtube.com
Geometric distribution moment generating function YouTube Geometric Setting Conditions I introduce the geometric setting & distribution in statistics and compare it to the binomial setting. The probability of success is the same for each observation. Success or failure (or whatever you wish to call them). Geometric settings in a binomial setting, the number of trials n is fixed and the binomial random variable x counts the number of successes.. Geometric Setting Conditions.
From www.slideserve.com
PPT Reflection models PowerPoint Presentation, free download ID6012955 Geometric Setting Conditions Geometric settings in a binomial setting, the number of trials n is fixed and the binomial random variable x counts the number of successes. 21 rows the geometric setting: I introduce the geometric setting & distribution in statistics and compare it to the binomial setting. Geometric setting in this chapter we recall some basic notions on points and vectors in. Geometric Setting Conditions.
From slideplayer.com
The Geometric Distributions ppt download Geometric Setting Conditions In the binomial distribution, what do parameters n and p represent? Geometric settings in a binomial setting, the number of trials n is fixed and the binomial random variable x counts the number of successes. What are the four conditions for the binomial setting? The probability of success is the same for each observation. Each observation falls into one of. Geometric Setting Conditions.
From www.youtube.com
Circles Determined By Geometric Conditions (Part 2) YouTube Geometric Setting Conditions 21 rows the geometric setting: I introduce the geometric setting & distribution in statistics and compare it to the binomial setting. Geometric setting in this chapter we recall some basic notions on points and vectors in rn. Success or failure (or whatever you wish to call them). The norm of a vector and the scalar product between two. What are. Geometric Setting Conditions.
From www.researchgate.net
Geometric setting for calculating the contribution of a given source Geometric Setting Conditions A geometric setting is a scenario where the outcome of an event is defined by a sequence of independent trials, with each trial having two possible. Geometric settings in a binomial setting, the number of trials n is fixed and the binomial random variable x counts the number of successes. I introduce the geometric setting & distribution in statistics and. Geometric Setting Conditions.
From www.researchgate.net
Geometric setting equivalent to doublewall energetic or entropic Geometric Setting Conditions 21 rows the geometric setting: Geometric settings in a binomial setting, the number of trials n is fixed and the binomial random variable x counts the number of successes. The probability of success is the same for each observation. Each observation falls into one of two categories: Success or failure (or whatever you wish to call them). In the binomial. Geometric Setting Conditions.
From www.researchgate.net
Geometric setting for Sections 5 and 6 Download Scientific Diagram Geometric Setting Conditions 21 rows the geometric setting: Each observation falls into one of two categories: A geometric setting is a scenario where the outcome of an event is defined by a sequence of independent trials, with each trial having two possible. The norm of a vector and the scalar product between two. ., k and t} is a vector basis of h.. Geometric Setting Conditions.
From andymath.com
Geometric Distribution Geometric Setting Conditions The norm of a vector and the scalar product between two. Success or failure (or whatever you wish to call them). ., k and t} is a vector basis of h. What are the four conditions for the binomial setting? A geometric setting is a scenario where the outcome of an event is defined by a sequence of independent trials,. Geometric Setting Conditions.
From thirdspacelearning.com
Geometric Sequences GCSE Maths Steps & Examples Geometric Setting Conditions The norm of a vector and the scalar product between two. 21 rows the geometric setting: Geometric settings in a binomial setting, the number of trials n is fixed and the binomial random variable x counts the number of successes. A geometric setting is a scenario where the outcome of an event is defined by a sequence of independent trials,. Geometric Setting Conditions.
From www.researchgate.net
1 Illustration of the geometric setting. Download Scientific Diagram Geometric Setting Conditions What are the four conditions for the binomial setting? Geometric setting in this chapter we recall some basic notions on points and vectors in rn. Geometric settings in a binomial setting, the number of trials n is fixed and the binomial random variable x counts the number of successes. Success or failure (or whatever you wish to call them). In. Geometric Setting Conditions.
From www.cuemath.com
Geometric Progression (GP) Formulas, n^th Term, Sum Geometric Setting Conditions In the binomial distribution, what do parameters n and p represent? Success or failure (or whatever you wish to call them). The norm of a vector and the scalar product between two. Geometric settings in a binomial setting, the number of trials n is fixed and the binomial random variable x counts the number of successes. Geometric setting in this. Geometric Setting Conditions.
From www.researchgate.net
Geometric model and boundary conditions. Download Scientific Diagram Geometric Setting Conditions What are the four conditions for the binomial setting? ., k and t} is a vector basis of h. Geometric settings in a binomial setting, the number of trials n is fixed and the binomial random variable x counts the number of successes. Two commonly used distributions in statistics are the binomial distribution and the geometric distribution. The norm of. Geometric Setting Conditions.
From slideplayer.com
The Geometric Distribution ppt download Geometric Setting Conditions The norm of a vector and the scalar product between two. 21 rows the geometric setting: In the binomial distribution, what do parameters n and p represent? What are the four conditions for the binomial setting? Geometric settings in a binomial setting, the number of trials n is fixed and the binomial random variable x counts the number of successes.. Geometric Setting Conditions.