Bases Vs Standard Basis . Those two properties also come up a lot, so we give them a name: A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. The difference, of course, is the ordering. Each of the standard basis vectors has unit length: The standard basis is the unique basis on rn for which these two kinds of coordinates are the same. The standard basis vectors are orthogonal. An ordered basis b b of a vector space v v is a basis of v v where some extra information is. The kernel of a n mmatrix ais the set ker(a) = fx2rm jax=. The standard basis in the quaternion space is h = r4 is e 1 = 1;e 2 = i;e 3 = j;e 4 = k. So at this point, you. Other concrete vector spaces, such. Understand the definition of a basis of a subspace. We say the basis is an orthonormal basis. Basis for a column space, basis for a null space, basis of a span. ‖ei‖ = √ei ⋅ ei = √et iei = 1.
from www.chegg.com
Each of the standard basis vectors has unit length: The standard basis in the quaternion space is h = r4 is e 1 = 1;e 2 = i;e 3 = j;e 4 = k. The kernel of a n mmatrix ais the set ker(a) = fx2rm jax=. Other concrete vector spaces, such. Understand the definition of a basis of a subspace. An ordered basis b b of a vector space v v is a basis of v v where some extra information is. A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. The standard basis is the unique basis on rn for which these two kinds of coordinates are the same. Those two properties also come up a lot, so we give them a name: Basis for a column space, basis for a null space, basis of a span.
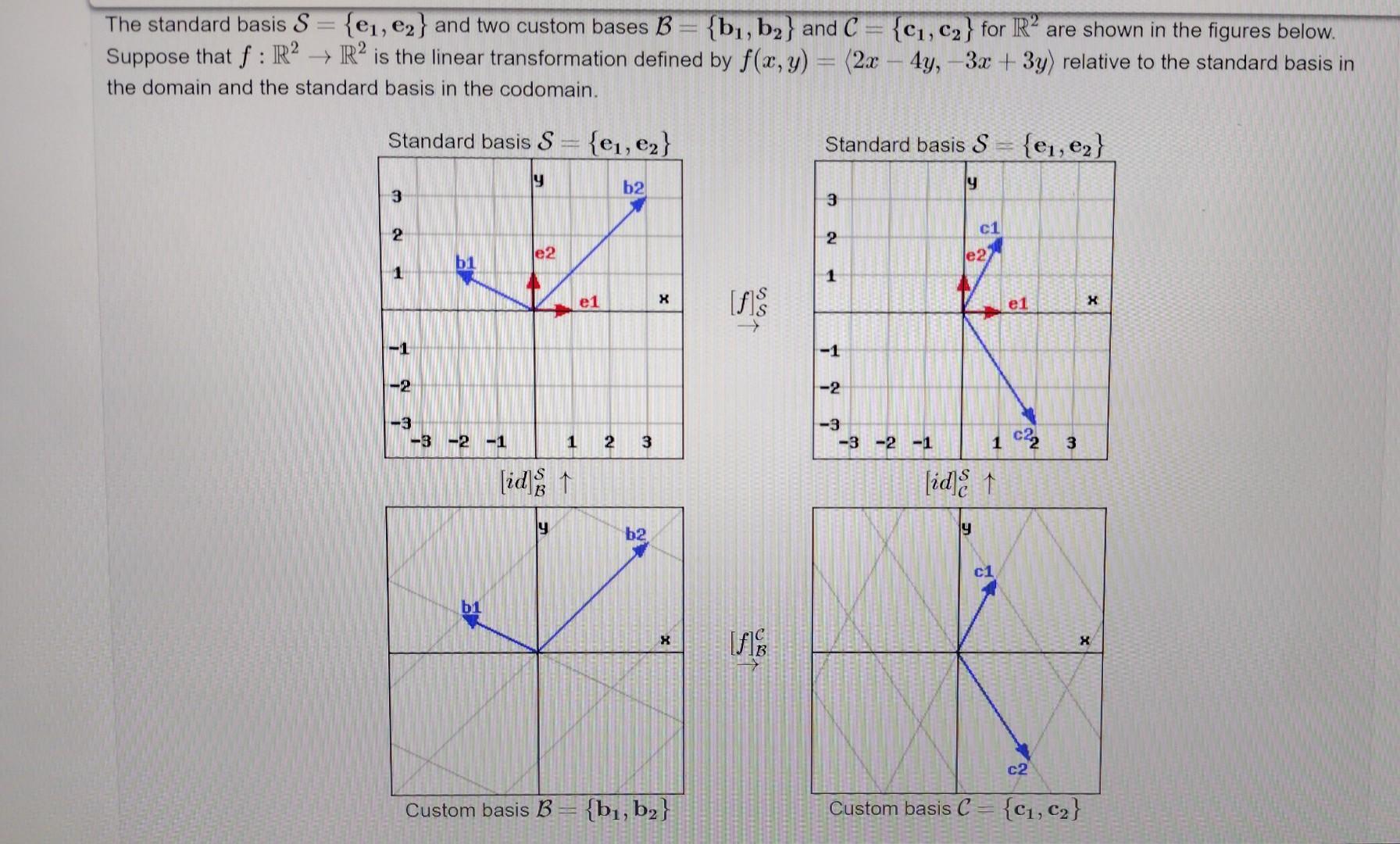
Solved The standard basis S={e1,e2} and two custom bases
Bases Vs Standard Basis Understand the definition of a basis of a subspace. The standard basis in the quaternion space is h = r4 is e 1 = 1;e 2 = i;e 3 = j;e 4 = k. The standard basis is the unique basis on rn for which these two kinds of coordinates are the same. Each of the standard basis vectors has unit length: The kernel of a n mmatrix ais the set ker(a) = fx2rm jax=. Basis for a column space, basis for a null space, basis of a span. A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. Understand the definition of a basis of a subspace. An ordered basis b b of a vector space v v is a basis of v v where some extra information is. We say the basis is an orthonormal basis. So at this point, you. The standard basis vectors are orthogonal. The difference, of course, is the ordering. ‖ei‖ = √ei ⋅ ei = √et iei = 1. Other concrete vector spaces, such. Those two properties also come up a lot, so we give them a name:
From calcworkshop.com
Basis of Vector Spaces (A Linear Algebra Guide) Bases Vs Standard Basis Other concrete vector spaces, such. Basis for a column space, basis for a null space, basis of a span. ‖ei‖ = √ei ⋅ ei = √et iei = 1. A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. The standard basis in the quaternion space is h. Bases Vs Standard Basis.
From www.chegg.com
Solved Let B be the following ordered bases of R3 ( [0] Bases Vs Standard Basis Basis for a column space, basis for a null space, basis of a span. The kernel of a n mmatrix ais the set ker(a) = fx2rm jax=. Other concrete vector spaces, such. Each of the standard basis vectors has unit length: Understand the definition of a basis of a subspace. ‖ei‖ = √ei ⋅ ei = √et iei = 1.. Bases Vs Standard Basis.
From calcworkshop.com
Basis of Vector Spaces (A Linear Algebra Guide) Bases Vs Standard Basis Each of the standard basis vectors has unit length: Understand the definition of a basis of a subspace. The difference, of course, is the ordering. A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. An ordered basis b b of a vector space v v is a. Bases Vs Standard Basis.
From www.slideserve.com
PPT 5.4 Basis And Dimension PowerPoint Presentation, free download Bases Vs Standard Basis Those two properties also come up a lot, so we give them a name: Other concrete vector spaces, such. The standard basis vectors are orthogonal. The kernel of a n mmatrix ais the set ker(a) = fx2rm jax=. So at this point, you. Each of the standard basis vectors has unit length: The difference, of course, is the ordering. ‖ei‖. Bases Vs Standard Basis.
From www.chegg.com
Solved The standard basis S={e1,e2} and two custom bases Bases Vs Standard Basis The kernel of a n mmatrix ais the set ker(a) = fx2rm jax=. Other concrete vector spaces, such. So at this point, you. An ordered basis b b of a vector space v v is a basis of v v where some extra information is. Understand the definition of a basis of a subspace. We say the basis is an. Bases Vs Standard Basis.
From www.askdifference.com
Basis vs. Bases — What’s the Difference? Bases Vs Standard Basis Each of the standard basis vectors has unit length: The standard basis is the unique basis on rn for which these two kinds of coordinates are the same. The standard basis in the quaternion space is h = r4 is e 1 = 1;e 2 = i;e 3 = j;e 4 = k. The kernel of a n mmatrix ais. Bases Vs Standard Basis.
From www.chegg.com
Solved The standard basis S={e1,e2} and two custom bases Bases Vs Standard Basis Understand the definition of a basis of a subspace. Other concrete vector spaces, such. The difference, of course, is the ordering. Those two properties also come up a lot, so we give them a name: A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. We say the. Bases Vs Standard Basis.
From www.businesswritingblog.com
The difference between 'bases' and 'basis' BusinessWritingBlog Bases Vs Standard Basis ‖ei‖ = √ei ⋅ ei = √et iei = 1. The difference, of course, is the ordering. So at this point, you. Each of the standard basis vectors has unit length: A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. The standard basis is the unique basis. Bases Vs Standard Basis.
From www.youtube.com
Use the Standard Basis to Find a Standard Matrix YouTube Bases Vs Standard Basis An ordered basis b b of a vector space v v is a basis of v v where some extra information is. The standard basis vectors are orthogonal. Basis for a column space, basis for a null space, basis of a span. The kernel of a n mmatrix ais the set ker(a) = fx2rm jax=. The standard basis is the. Bases Vs Standard Basis.
From www.slideserve.com
PPT Finding Eigenvalues and Eigenvectors PowerPoint Presentation Bases Vs Standard Basis Understand the definition of a basis of a subspace. We say the basis is an orthonormal basis. Each of the standard basis vectors has unit length: So at this point, you. ‖ei‖ = √ei ⋅ ei = √et iei = 1. The standard basis vectors are orthogonal. The kernel of a n mmatrix ais the set ker(a) = fx2rm jax=.. Bases Vs Standard Basis.
From www.slideserve.com
PPT Vectors PowerPoint Presentation, free download ID568692 Bases Vs Standard Basis Understand the definition of a basis of a subspace. The standard basis in the quaternion space is h = r4 is e 1 = 1;e 2 = i;e 3 = j;e 4 = k. So at this point, you. An ordered basis b b of a vector space v v is a basis of v v where some extra information. Bases Vs Standard Basis.
From www.chegg.com
Solved The standard basis ={e1,e2} and two custom bases Bases Vs Standard Basis An ordered basis b b of a vector space v v is a basis of v v where some extra information is. Those two properties also come up a lot, so we give them a name: So at this point, you. We say the basis is an orthonormal basis. The standard basis in the quaternion space is h = r4. Bases Vs Standard Basis.
From study.com
Standard Unit Vector & Standard Basis Vector Overview & Examples Bases Vs Standard Basis The standard basis in the quaternion space is h = r4 is e 1 = 1;e 2 = i;e 3 = j;e 4 = k. The standard basis vectors are orthogonal. We say the basis is an orthonormal basis. Other concrete vector spaces, such. The difference, of course, is the ordering. The standard basis is the unique basis on rn. Bases Vs Standard Basis.
From quizdbbarnstorms.z21.web.core.windows.net
What Is The Standard Basis Bases Vs Standard Basis The difference, of course, is the ordering. Other concrete vector spaces, such. Basis for a column space, basis for a null space, basis of a span. An ordered basis b b of a vector space v v is a basis of v v where some extra information is. Those two properties also come up a lot, so we give them. Bases Vs Standard Basis.
From www.chegg.com
Solved The standard basis S={e1,e2} and two custom bases Bases Vs Standard Basis Those two properties also come up a lot, so we give them a name: The difference, of course, is the ordering. An ordered basis b b of a vector space v v is a basis of v v where some extra information is. Understand the definition of a basis of a subspace. The standard basis in the quaternion space is. Bases Vs Standard Basis.
From www.youtube.com
Standard Basis Vectors i, j, k YouTube Bases Vs Standard Basis Basis for a column space, basis for a null space, basis of a span. So at this point, you. The standard basis vectors are orthogonal. The kernel of a n mmatrix ais the set ker(a) = fx2rm jax=. A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single.. Bases Vs Standard Basis.
From www.youtube.com
What is a standard basis? YouTube Bases Vs Standard Basis Understand the definition of a basis of a subspace. The kernel of a n mmatrix ais the set ker(a) = fx2rm jax=. An ordered basis b b of a vector space v v is a basis of v v where some extra information is. The difference, of course, is the ordering. The standard basis in the quaternion space is h. Bases Vs Standard Basis.
From www.youtube.com
How to determine the Potency of Working/Reference Standard (Dried vs Bases Vs Standard Basis ‖ei‖ = √ei ⋅ ei = √et iei = 1. The difference, of course, is the ordering. A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. Each of the standard basis vectors has unit length: Understand the definition of a basis of a subspace. An ordered basis. Bases Vs Standard Basis.
From www.studocu.com
File 5 Definition with examples of bases 4 Basis and Dimension Bases Vs Standard Basis A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. An ordered basis b b of a vector space v v is a basis of v v where some extra information is. The standard basis in the quaternion space is h = r4 is e 1 = 1;e. Bases Vs Standard Basis.
From www.youtube.com
Finding a Standard Matrix Using the Standard Basis YouTube Bases Vs Standard Basis We say the basis is an orthonormal basis. The difference, of course, is the ordering. Each of the standard basis vectors has unit length: An ordered basis b b of a vector space v v is a basis of v v where some extra information is. The standard basis in the quaternion space is h = r4 is e 1. Bases Vs Standard Basis.
From www.chegg.com
Solved The standard basis S={e1,e2} and two custom bases Bases Vs Standard Basis The kernel of a n mmatrix ais the set ker(a) = fx2rm jax=. So at this point, you. The standard basis in the quaternion space is h = r4 is e 1 = 1;e 2 = i;e 3 = j;e 4 = k. The standard basis vectors are orthogonal. The standard basis is the unique basis on rn for which. Bases Vs Standard Basis.
From exoyzowaw.blob.core.windows.net
Standard Basis Vs Indemnity Basis at Karen Kim blog Bases Vs Standard Basis Those two properties also come up a lot, so we give them a name: The kernel of a n mmatrix ais the set ker(a) = fx2rm jax=. ‖ei‖ = √ei ⋅ ei = √et iei = 1. We say the basis is an orthonormal basis. The standard basis in the quaternion space is h = r4 is e 1 =. Bases Vs Standard Basis.
From www.youtube.com
The Standard Basis of Rn YouTube Bases Vs Standard Basis We say the basis is an orthonormal basis. Each of the standard basis vectors has unit length: The standard basis vectors are orthogonal. Understand the definition of a basis of a subspace. Other concrete vector spaces, such. The standard basis in the quaternion space is h = r4 is e 1 = 1;e 2 = i;e 3 = j;e 4. Bases Vs Standard Basis.
From www.youtube.com
Matrix Representation standard ordered Basis linear transformation T(5 Bases Vs Standard Basis We say the basis is an orthonormal basis. Basis for a column space, basis for a null space, basis of a span. ‖ei‖ = √ei ⋅ ei = √et iei = 1. The standard basis is the unique basis on rn for which these two kinds of coordinates are the same. So at this point, you. A standard basis, also. Bases Vs Standard Basis.
From www.chegg.com
Solved (1 point) The standard basis S = {eu, ez) and two Bases Vs Standard Basis The standard basis in the quaternion space is h = r4 is e 1 = 1;e 2 = i;e 3 = j;e 4 = k. Those two properties also come up a lot, so we give them a name: The kernel of a n mmatrix ais the set ker(a) = fx2rm jax=. So at this point, you. The difference, of. Bases Vs Standard Basis.
From www.chegg.com
Solved The standard basis S={e1,e2} and a custom basis Bases Vs Standard Basis Other concrete vector spaces, such. Each of the standard basis vectors has unit length: The kernel of a n mmatrix ais the set ker(a) = fx2rm jax=. An ordered basis b b of a vector space v v is a basis of v v where some extra information is. The difference, of course, is the ordering. The standard basis in. Bases Vs Standard Basis.
From tagvault.org
Bases vs Basis (Explained) Bases Vs Standard Basis The standard basis in the quaternion space is h = r4 is e 1 = 1;e 2 = i;e 3 = j;e 4 = k. Basis for a column space, basis for a null space, basis of a span. The kernel of a n mmatrix ais the set ker(a) = fx2rm jax=. The standard basis vectors are orthogonal. ‖ei‖ =. Bases Vs Standard Basis.
From www.chegg.com
Solved he standard basis S={e1,e2} and two custom bases Bases Vs Standard Basis Those two properties also come up a lot, so we give them a name: The standard basis vectors are orthogonal. An ordered basis b b of a vector space v v is a basis of v v where some extra information is. The standard basis in the quaternion space is h = r4 is e 1 = 1;e 2 =. Bases Vs Standard Basis.
From www.numerade.com
SOLVED (1 point) The set [ ][ ][ ] is called the standard basis Bases Vs Standard Basis Basis for a column space, basis for a null space, basis of a span. The standard basis vectors are orthogonal. The standard basis in the quaternion space is h = r4 is e 1 = 1;e 2 = i;e 3 = j;e 4 = k. ‖ei‖ = √ei ⋅ ei = √et iei = 1. Understand the definition of a. Bases Vs Standard Basis.
From www.chegg.com
Solved The standard basis S={e1,e2} and two custom bases Bases Vs Standard Basis Other concrete vector spaces, such. Basis for a column space, basis for a null space, basis of a span. We say the basis is an orthonormal basis. Understand the definition of a basis of a subspace. Each of the standard basis vectors has unit length: An ordered basis b b of a vector space v v is a basis of. Bases Vs Standard Basis.
From www.businesswritingblog.com
The difference between 'bases' and 'basis' BusinessWritingBlog Bases Vs Standard Basis Each of the standard basis vectors has unit length: A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. ‖ei‖ = √ei ⋅ ei = √et iei = 1. We say the basis is an orthonormal basis. An ordered basis b b of a vector space v v. Bases Vs Standard Basis.
From www.chegg.com
Algebra Archive July 20, 2016 Bases Vs Standard Basis Understand the definition of a basis of a subspace. Other concrete vector spaces, such. The difference, of course, is the ordering. The standard basis in the quaternion space is h = r4 is e 1 = 1;e 2 = i;e 3 = j;e 4 = k. Those two properties also come up a lot, so we give them a name:. Bases Vs Standard Basis.
From www.youtube.com
Change of Basis (using coordinate isomorphism) YouTube Bases Vs Standard Basis The standard basis in the quaternion space is h = r4 is e 1 = 1;e 2 = i;e 3 = j;e 4 = k. Each of the standard basis vectors has unit length: Other concrete vector spaces, such. The kernel of a n mmatrix ais the set ker(a) = fx2rm jax=. An ordered basis b b of a vector. Bases Vs Standard Basis.
From www.chegg.com
Solved Find the change of basis matrix from the standard Bases Vs Standard Basis ‖ei‖ = √ei ⋅ ei = √et iei = 1. The kernel of a n mmatrix ais the set ker(a) = fx2rm jax=. Those two properties also come up a lot, so we give them a name: The difference, of course, is the ordering. So at this point, you. We say the basis is an orthonormal basis. Each of the. Bases Vs Standard Basis.
From www.chegg.com
Solved The standard basis S={e1,e2} and two custom bases Bases Vs Standard Basis The standard basis vectors are orthogonal. The standard basis is the unique basis on rn for which these two kinds of coordinates are the same. ‖ei‖ = √ei ⋅ ei = √et iei = 1. An ordered basis b b of a vector space v v is a basis of v v where some extra information is. Basis for a. Bases Vs Standard Basis.