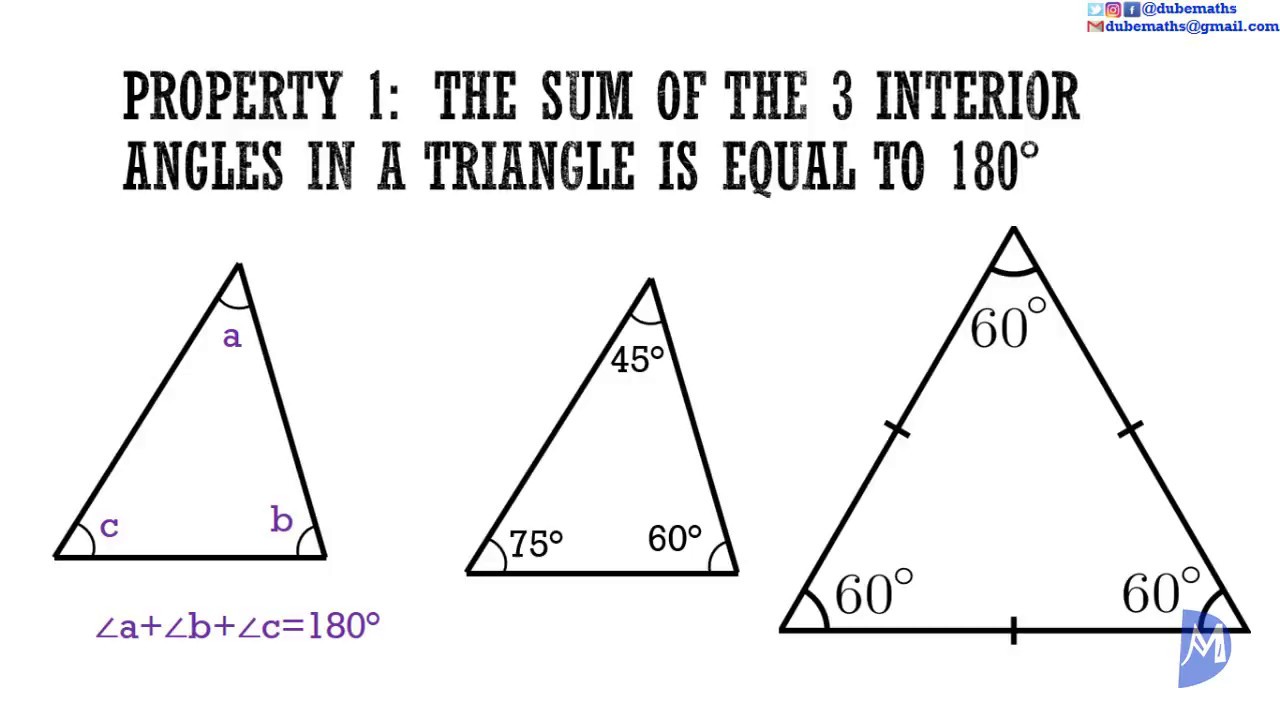
How Do You Know If A Triangle Does Not Exist . No triangle exists (a <b) in this case a <b and side a is too short to reach the base of the triangle. \(\angle a=112^{\circ}, \quad a=45, \quad b=24\) round the angles and side lengths to the nearest \(10^{t h}\) solution. If you're given 3 side measurements, there's a quick way to determine if those three sides can form a triangle. See if you are given two sides and the angle not in between (ssa). Follow along with this tutorial. That is, you can know what a triangle is without. We need to find the measure of angle b using the law of sines: If their sum is less than 180°, we know a triangle can exist. Consider the following cases given a, b, and ∠a: It's easy to prove that the triangle inequality holds for any triangle with the lengths of sides a a, b b and c c. But how can one prove. The point of this passage is that the existence of a triangle does not follow from the definition.
from classcampusenrique.z19.web.core.windows.net
If their sum is less than 180°, we know a triangle can exist. Consider the following cases given a, b, and ∠a: But how can one prove. Follow along with this tutorial. See if you are given two sides and the angle not in between (ssa). The point of this passage is that the existence of a triangle does not follow from the definition. We need to find the measure of angle b using the law of sines: No triangle exists (a <b) in this case a <b and side a is too short to reach the base of the triangle. It's easy to prove that the triangle inequality holds for any triangle with the lengths of sides a a, b b and c c. That is, you can know what a triangle is without.
Properties Of A Triangle In Geometry
How Do You Know If A Triangle Does Not Exist No triangle exists (a <b) in this case a <b and side a is too short to reach the base of the triangle. See if you are given two sides and the angle not in between (ssa). If their sum is less than 180°, we know a triangle can exist. Follow along with this tutorial. Consider the following cases given a, b, and ∠a: That is, you can know what a triangle is without. But how can one prove. It's easy to prove that the triangle inequality holds for any triangle with the lengths of sides a a, b b and c c. \(\angle a=112^{\circ}, \quad a=45, \quad b=24\) round the angles and side lengths to the nearest \(10^{t h}\) solution. If you're given 3 side measurements, there's a quick way to determine if those three sides can form a triangle. The point of this passage is that the existence of a triangle does not follow from the definition. No triangle exists (a <b) in this case a <b and side a is too short to reach the base of the triangle. We need to find the measure of angle b using the law of sines:
From www.chegg.com
Solved Solve triangle ABC. (If an answer does not exist, How Do You Know If A Triangle Does Not Exist If their sum is less than 180°, we know a triangle can exist. We need to find the measure of angle b using the law of sines: Consider the following cases given a, b, and ∠a: If you're given 3 side measurements, there's a quick way to determine if those three sides can form a triangle. \(\angle a=112^{\circ}, \quad a=45,. How Do You Know If A Triangle Does Not Exist.
From www.youtube.com
How To Calculate The Missing Side Length of a Triangle YouTube How Do You Know If A Triangle Does Not Exist Follow along with this tutorial. \(\angle a=112^{\circ}, \quad a=45, \quad b=24\) round the angles and side lengths to the nearest \(10^{t h}\) solution. That is, you can know what a triangle is without. We need to find the measure of angle b using the law of sines: If you're given 3 side measurements, there's a quick way to determine if. How Do You Know If A Triangle Does Not Exist.
From www.youtube.com
Triangle Congruence Theorems, Two Column Proofs, SSS, SAS, ASA, AAS How Do You Know If A Triangle Does Not Exist That is, you can know what a triangle is without. See if you are given two sides and the angle not in between (ssa). The point of this passage is that the existence of a triangle does not follow from the definition. \(\angle a=112^{\circ}, \quad a=45, \quad b=24\) round the angles and side lengths to the nearest \(10^{t h}\) solution.. How Do You Know If A Triangle Does Not Exist.
From www.chegg.com
Solved Solve triangle ABC. (If an answer does not exist, How Do You Know If A Triangle Does Not Exist That is, you can know what a triangle is without. It's easy to prove that the triangle inequality holds for any triangle with the lengths of sides a a, b b and c c. If you're given 3 side measurements, there's a quick way to determine if those three sides can form a triangle. The point of this passage is. How Do You Know If A Triangle Does Not Exist.
From www.cuemath.com
Congruence in Triangles Meaning, Properties, Congruent Triangles How Do You Know If A Triangle Does Not Exist Follow along with this tutorial. Consider the following cases given a, b, and ∠a: No triangle exists (a <b) in this case a <b and side a is too short to reach the base of the triangle. That is, you can know what a triangle is without. If their sum is less than 180°, we know a triangle can exist.. How Do You Know If A Triangle Does Not Exist.
From classcampusenrique.z19.web.core.windows.net
Properties Of A Triangle In Geometry How Do You Know If A Triangle Does Not Exist Follow along with this tutorial. If you're given 3 side measurements, there's a quick way to determine if those three sides can form a triangle. The point of this passage is that the existence of a triangle does not follow from the definition. That is, you can know what a triangle is without. We need to find the measure of. How Do You Know If A Triangle Does Not Exist.
From www.onlinemathlearning.com
Using Similar Triangles (examples, solutions, videos, lessons How Do You Know If A Triangle Does Not Exist Consider the following cases given a, b, and ∠a: If you're given 3 side measurements, there's a quick way to determine if those three sides can form a triangle. We need to find the measure of angle b using the law of sines: \(\angle a=112^{\circ}, \quad a=45, \quad b=24\) round the angles and side lengths to the nearest \(10^{t h}\). How Do You Know If A Triangle Does Not Exist.
From e-gmat.com
Properties of Triangle types & formulas [Video & Practice] How Do You Know If A Triangle Does Not Exist See if you are given two sides and the angle not in between (ssa). That is, you can know what a triangle is without. The point of this passage is that the existence of a triangle does not follow from the definition. It's easy to prove that the triangle inequality holds for any triangle with the lengths of sides a. How Do You Know If A Triangle Does Not Exist.
From www.chegg.com
Solved Solve triangle ABC. (If an answer does not exist, How Do You Know If A Triangle Does Not Exist If you're given 3 side measurements, there's a quick way to determine if those three sides can form a triangle. \(\angle a=112^{\circ}, \quad a=45, \quad b=24\) round the angles and side lengths to the nearest \(10^{t h}\) solution. No triangle exists (a <b) in this case a <b and side a is too short to reach the base of the. How Do You Know If A Triangle Does Not Exist.
From www.chegg.com
Solved Solve triangle ABC. (If an answer does not exist, How Do You Know If A Triangle Does Not Exist If their sum is less than 180°, we know a triangle can exist. See if you are given two sides and the angle not in between (ssa). The point of this passage is that the existence of a triangle does not follow from the definition. Consider the following cases given a, b, and ∠a: But how can one prove. It's. How Do You Know If A Triangle Does Not Exist.
From www.worksheetscity.com
How Many Corners Does A Triangle Have Worksheetsr WorksheetsCity How Do You Know If A Triangle Does Not Exist It's easy to prove that the triangle inequality holds for any triangle with the lengths of sides a a, b b and c c. The point of this passage is that the existence of a triangle does not follow from the definition. Consider the following cases given a, b, and ∠a: But how can one prove. No triangle exists (a. How Do You Know If A Triangle Does Not Exist.
From www.chegg.com
Solved Solve triangle ABC. (If an answer does not exist, How Do You Know If A Triangle Does Not Exist The point of this passage is that the existence of a triangle does not follow from the definition. No triangle exists (a <b) in this case a <b and side a is too short to reach the base of the triangle. \(\angle a=112^{\circ}, \quad a=45, \quad b=24\) round the angles and side lengths to the nearest \(10^{t h}\) solution. Follow. How Do You Know If A Triangle Does Not Exist.
From www.chilimath.com
Classifying Triangles by Angles ChiliMath How Do You Know If A Triangle Does Not Exist No triangle exists (a <b) in this case a <b and side a is too short to reach the base of the triangle. It's easy to prove that the triangle inequality holds for any triangle with the lengths of sides a a, b b and c c. The point of this passage is that the existence of a triangle does. How Do You Know If A Triangle Does Not Exist.
From www.youtube.com
naming congruent triangles YouTube How Do You Know If A Triangle Does Not Exist The point of this passage is that the existence of a triangle does not follow from the definition. We need to find the measure of angle b using the law of sines: See if you are given two sides and the angle not in between (ssa). If their sum is less than 180°, we know a triangle can exist. Follow. How Do You Know If A Triangle Does Not Exist.
From www.grc.nasa.gov
Trigonometry Terminology How Do You Know If A Triangle Does Not Exist No triangle exists (a <b) in this case a <b and side a is too short to reach the base of the triangle. But how can one prove. \(\angle a=112^{\circ}, \quad a=45, \quad b=24\) round the angles and side lengths to the nearest \(10^{t h}\) solution. The point of this passage is that the existence of a triangle does not. How Do You Know If A Triangle Does Not Exist.
From www.storyofmathematics.com
Case 2 How Do You Know If A Triangle Does Not Exist But how can one prove. If their sum is less than 180°, we know a triangle can exist. We need to find the measure of angle b using the law of sines: That is, you can know what a triangle is without. If you're given 3 side measurements, there's a quick way to determine if those three sides can form. How Do You Know If A Triangle Does Not Exist.
From mathmonks.com
Isosceles Triangle Definition, Properties, Types, Formulas How Do You Know If A Triangle Does Not Exist Consider the following cases given a, b, and ∠a: But how can one prove. We need to find the measure of angle b using the law of sines: No triangle exists (a <b) in this case a <b and side a is too short to reach the base of the triangle. \(\angle a=112^{\circ}, \quad a=45, \quad b=24\) round the angles. How Do You Know If A Triangle Does Not Exist.
From thirdspacelearning.com
Angles In A Triangle GCSE Maths Steps, Examples & Worksheet How Do You Know If A Triangle Does Not Exist It's easy to prove that the triangle inequality holds for any triangle with the lengths of sides a a, b b and c c. If you're given 3 side measurements, there's a quick way to determine if those three sides can form a triangle. \(\angle a=112^{\circ}, \quad a=45, \quad b=24\) round the angles and side lengths to the nearest \(10^{t. How Do You Know If A Triangle Does Not Exist.
From www.thoughtco.com
Types of Triangles Acute and Obtuse How Do You Know If A Triangle Does Not Exist \(\angle a=112^{\circ}, \quad a=45, \quad b=24\) round the angles and side lengths to the nearest \(10^{t h}\) solution. See if you are given two sides and the angle not in between (ssa). The point of this passage is that the existence of a triangle does not follow from the definition. If their sum is less than 180°, we know a. How Do You Know If A Triangle Does Not Exist.
From lessonmagiccoaching.z21.web.core.windows.net
How To Solve Right Triangles In Geometry How Do You Know If A Triangle Does Not Exist Consider the following cases given a, b, and ∠a: If you're given 3 side measurements, there's a quick way to determine if those three sides can form a triangle. It's easy to prove that the triangle inequality holds for any triangle with the lengths of sides a a, b b and c c. We need to find the measure of. How Do You Know If A Triangle Does Not Exist.
From worksheetzoneetiolin.z5.web.core.windows.net
Triangle Congruence Geometry Worksheet How Do You Know If A Triangle Does Not Exist If you're given 3 side measurements, there's a quick way to determine if those three sides can form a triangle. But how can one prove. It's easy to prove that the triangle inequality holds for any triangle with the lengths of sides a a, b b and c c. No triangle exists (a <b) in this case a <b and. How Do You Know If A Triangle Does Not Exist.
From www.youtube.com
maxresdefault.jpg How Do You Know If A Triangle Does Not Exist If you're given 3 side measurements, there's a quick way to determine if those three sides can form a triangle. That is, you can know what a triangle is without. See if you are given two sides and the angle not in between (ssa). But how can one prove. \(\angle a=112^{\circ}, \quad a=45, \quad b=24\) round the angles and side. How Do You Know If A Triangle Does Not Exist.
From calcworkshop.com
Classifying Triangles (15+ StepbyStep Examples!) How Do You Know If A Triangle Does Not Exist No triangle exists (a <b) in this case a <b and side a is too short to reach the base of the triangle. That is, you can know what a triangle is without. Follow along with this tutorial. It's easy to prove that the triangle inequality holds for any triangle with the lengths of sides a a, b b and. How Do You Know If A Triangle Does Not Exist.
From www.zmescience.com
Types of triangles and other triangle facts How Do You Know If A Triangle Does Not Exist If their sum is less than 180°, we know a triangle can exist. Follow along with this tutorial. It's easy to prove that the triangle inequality holds for any triangle with the lengths of sides a a, b b and c c. \(\angle a=112^{\circ}, \quad a=45, \quad b=24\) round the angles and side lengths to the nearest \(10^{t h}\) solution.. How Do You Know If A Triangle Does Not Exist.
From owlcation.com
How to Calculate the Sides and Angles of Triangles Using Pythagoras How Do You Know If A Triangle Does Not Exist That is, you can know what a triangle is without. If you're given 3 side measurements, there's a quick way to determine if those three sides can form a triangle. The point of this passage is that the existence of a triangle does not follow from the definition. Follow along with this tutorial. Consider the following cases given a, b,. How Do You Know If A Triangle Does Not Exist.
From mathmonks.com
Similar Triangles Definition, Properties, Formulas, Examples How Do You Know If A Triangle Does Not Exist If you're given 3 side measurements, there's a quick way to determine if those three sides can form a triangle. See if you are given two sides and the angle not in between (ssa). If their sum is less than 180°, we know a triangle can exist. \(\angle a=112^{\circ}, \quad a=45, \quad b=24\) round the angles and side lengths to. How Do You Know If A Triangle Does Not Exist.
From www.chegg.com
Solved Solve triangle ABC. (If an answer does not exist, How Do You Know If A Triangle Does Not Exist We need to find the measure of angle b using the law of sines: If their sum is less than 180°, we know a triangle can exist. \(\angle a=112^{\circ}, \quad a=45, \quad b=24\) round the angles and side lengths to the nearest \(10^{t h}\) solution. Follow along with this tutorial. See if you are given two sides and the angle. How Do You Know If A Triangle Does Not Exist.
From www.youtube.com
Geometry how to prove triangle congruent congruency sas sss asa How Do You Know If A Triangle Does Not Exist We need to find the measure of angle b using the law of sines: See if you are given two sides and the angle not in between (ssa). Consider the following cases given a, b, and ∠a: But how can one prove. The point of this passage is that the existence of a triangle does not follow from the definition.. How Do You Know If A Triangle Does Not Exist.
From www.reddit.com
[10th grade geometry] determine if the triangle is sss, sas, asa, aas How Do You Know If A Triangle Does Not Exist Follow along with this tutorial. That is, you can know what a triangle is without. If you're given 3 side measurements, there's a quick way to determine if those three sides can form a triangle. See if you are given two sides and the angle not in between (ssa). We need to find the measure of angle b using the. How Do You Know If A Triangle Does Not Exist.
From owlcation.com
How to Calculate the Sides and Angles of Triangles Using Pythagoras How Do You Know If A Triangle Does Not Exist But how can one prove. The point of this passage is that the existence of a triangle does not follow from the definition. That is, you can know what a triangle is without. Follow along with this tutorial. \(\angle a=112^{\circ}, \quad a=45, \quad b=24\) round the angles and side lengths to the nearest \(10^{t h}\) solution. No triangle exists (a. How Do You Know If A Triangle Does Not Exist.
From mungfali.com
How To Calculate The Sides And Angles Of Triangles Owlcation DC3 How Do You Know If A Triangle Does Not Exist That is, you can know what a triangle is without. If you're given 3 side measurements, there's a quick way to determine if those three sides can form a triangle. If their sum is less than 180°, we know a triangle can exist. It's easy to prove that the triangle inequality holds for any triangle with the lengths of sides. How Do You Know If A Triangle Does Not Exist.
From www.cuemath.com
Triangles Definition, Properties, Formula Triangle Shape How Do You Know If A Triangle Does Not Exist No triangle exists (a <b) in this case a <b and side a is too short to reach the base of the triangle. If you're given 3 side measurements, there's a quick way to determine if those three sides can form a triangle. But how can one prove. See if you are given two sides and the angle not in. How Do You Know If A Triangle Does Not Exist.
From manualfixfaber.z19.web.core.windows.net
Triangle Angle Measurements Worksheet How Do You Know If A Triangle Does Not Exist See if you are given two sides and the angle not in between (ssa). Consider the following cases given a, b, and ∠a: But how can one prove. No triangle exists (a <b) in this case a <b and side a is too short to reach the base of the triangle. It's easy to prove that the triangle inequality holds. How Do You Know If A Triangle Does Not Exist.
From educationgrafts.z21.web.core.windows.net
What Does The Triangle How Do You Know If A Triangle Does Not Exist That is, you can know what a triangle is without. If their sum is less than 180°, we know a triangle can exist. If you're given 3 side measurements, there's a quick way to determine if those three sides can form a triangle. But how can one prove. The point of this passage is that the existence of a triangle. How Do You Know If A Triangle Does Not Exist.
From www.mometrix.com
Different Types of Triangles (Video & Practice) How Do You Know If A Triangle Does Not Exist \(\angle a=112^{\circ}, \quad a=45, \quad b=24\) round the angles and side lengths to the nearest \(10^{t h}\) solution. It's easy to prove that the triangle inequality holds for any triangle with the lengths of sides a a, b b and c c. If their sum is less than 180°, we know a triangle can exist. Consider the following cases given. How Do You Know If A Triangle Does Not Exist.