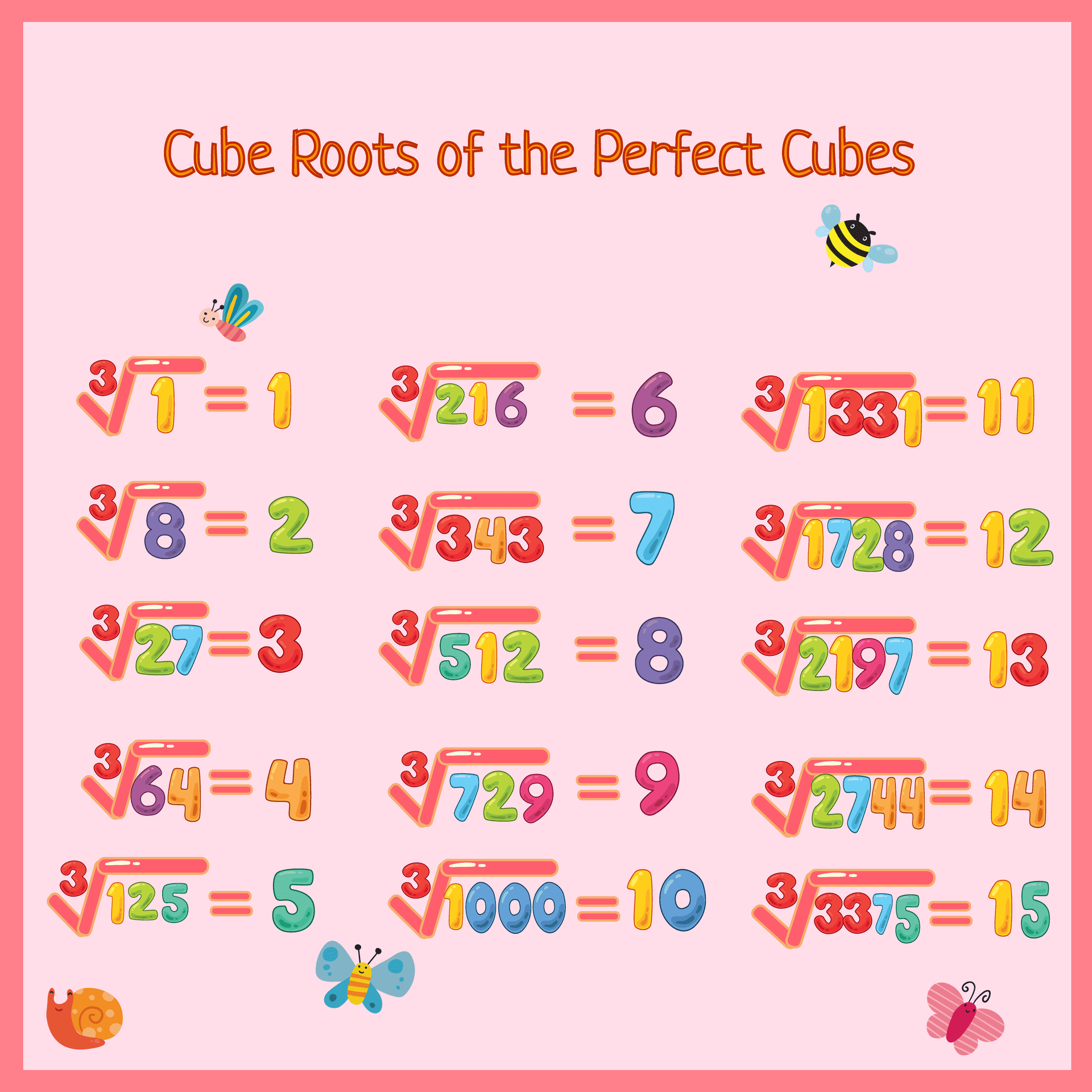Field Extension Cube Root . Show that this element is algebraic. I have the following problem that i am stuck on: An extension field \(e\) of a field \(f\) is an algebraic extension of \(f\) if every element in \(e\) is algebraic over \(f\text{.}\) if \(e\) is a. I'm trying to find a basis for the field extension q(ζ, 3√2) / q, where ζ is the cube root of unity. Given a field \(k\) and a polynomial \(f(x)\in k[x]\), how can we find a field extension \(l/k\) containing some root \(\theta\) of \(f(x)\)?. Let fbe the field of rational numbers, and let be a cube root of 2. Here's a primitive example of a field extension: Interestingly, we can often build a new field from an existing one through a process known as field extension, where additional elements are. $\mathbb{q}(\sqrt 2) = \{a + b\sqrt 2 \;|\; The dimension dim f kof kis called the degree of this extension, or the. It's easy to show that it is a. F] of the field extension. I attempted this with starting with a set of.
from youvegotthismath.com
It's easy to show that it is a. Given a field \(k\) and a polynomial \(f(x)\in k[x]\), how can we find a field extension \(l/k\) containing some root \(\theta\) of \(f(x)\)?. I have the following problem that i am stuck on: Let fbe the field of rational numbers, and let be a cube root of 2. The dimension dim f kof kis called the degree of this extension, or the. Here's a primitive example of a field extension: F] of the field extension. I'm trying to find a basis for the field extension q(ζ, 3√2) / q, where ζ is the cube root of unity. Show that this element is algebraic. I attempted this with starting with a set of.
10 Square Root and Cube Root Worksheet Free Printable
Field Extension Cube Root Interestingly, we can often build a new field from an existing one through a process known as field extension, where additional elements are. I attempted this with starting with a set of. Interestingly, we can often build a new field from an existing one through a process known as field extension, where additional elements are. I have the following problem that i am stuck on: Given a field \(k\) and a polynomial \(f(x)\in k[x]\), how can we find a field extension \(l/k\) containing some root \(\theta\) of \(f(x)\)?. I'm trying to find a basis for the field extension q(ζ, 3√2) / q, where ζ is the cube root of unity. Here's a primitive example of a field extension: The dimension dim f kof kis called the degree of this extension, or the. $\mathbb{q}(\sqrt 2) = \{a + b\sqrt 2 \;|\; Let fbe the field of rational numbers, and let be a cube root of 2. Show that this element is algebraic. It's easy to show that it is a. An extension field \(e\) of a field \(f\) is an algebraic extension of \(f\) if every element in \(e\) is algebraic over \(f\text{.}\) if \(e\) is a. F] of the field extension.
From www.numerade.com
SOLVEDFind the root field of a(x)=(x^23)(x^31) over 𝐐 . ANSWER The Field Extension Cube Root Given a field \(k\) and a polynomial \(f(x)\in k[x]\), how can we find a field extension \(l/k\) containing some root \(\theta\) of \(f(x)\)?. I attempted this with starting with a set of. Show that this element is algebraic. F] of the field extension. It's easy to show that it is a. An extension field \(e\) of a field \(f\) is. Field Extension Cube Root.
From www.youtube.com
square root and cube root tricks YouTube Field Extension Cube Root Let fbe the field of rational numbers, and let be a cube root of 2. Given a field \(k\) and a polynomial \(f(x)\in k[x]\), how can we find a field extension \(l/k\) containing some root \(\theta\) of \(f(x)\)?. Show that this element is algebraic. I attempted this with starting with a set of. I have the following problem that i. Field Extension Cube Root.
From thirdspacelearning.com
Cube Numbers and Cube Roots GCSE Maths Guide & Examples Field Extension Cube Root An extension field \(e\) of a field \(f\) is an algebraic extension of \(f\) if every element in \(e\) is algebraic over \(f\text{.}\) if \(e\) is a. Given a field \(k\) and a polynomial \(f(x)\in k[x]\), how can we find a field extension \(l/k\) containing some root \(\theta\) of \(f(x)\)?. I attempted this with starting with a set of. Interestingly,. Field Extension Cube Root.
From studylib.net
Cubes and Cube Roots Homework Field Extension Cube Root Given a field \(k\) and a polynomial \(f(x)\in k[x]\), how can we find a field extension \(l/k\) containing some root \(\theta\) of \(f(x)\)?. $\mathbb{q}(\sqrt 2) = \{a + b\sqrt 2 \;|\; I'm trying to find a basis for the field extension q(ζ, 3√2) / q, where ζ is the cube root of unity. I attempted this with starting with a. Field Extension Cube Root.
From www.chegg.com
Solved 1. This exercise determines the splitting field K for Field Extension Cube Root An extension field \(e\) of a field \(f\) is an algebraic extension of \(f\) if every element in \(e\) is algebraic over \(f\text{.}\) if \(e\) is a. F] of the field extension. It's easy to show that it is a. Let fbe the field of rational numbers, and let be a cube root of 2. Here's a primitive example of. Field Extension Cube Root.
From www.youtube.com
Inverse of cube/cuberoot function YouTube Field Extension Cube Root An extension field \(e\) of a field \(f\) is an algebraic extension of \(f\) if every element in \(e\) is algebraic over \(f\text{.}\) if \(e\) is a. Interestingly, we can often build a new field from an existing one through a process known as field extension, where additional elements are. I have the following problem that i am stuck on:. Field Extension Cube Root.
From www.slideserve.com
PPT Field Extension PowerPoint Presentation, free download ID1777745 Field Extension Cube Root It's easy to show that it is a. $\mathbb{q}(\sqrt 2) = \{a + b\sqrt 2 \;|\; I attempted this with starting with a set of. I have the following problem that i am stuck on: Show that this element is algebraic. Given a field \(k\) and a polynomial \(f(x)\in k[x]\), how can we find a field extension \(l/k\) containing some. Field Extension Cube Root.
From www.youtube.com
Square Root & Cube Root in Mathematics (Lecture9) YouTube Field Extension Cube Root An extension field \(e\) of a field \(f\) is an algebraic extension of \(f\) if every element in \(e\) is algebraic over \(f\text{.}\) if \(e\) is a. Let fbe the field of rational numbers, and let be a cube root of 2. I attempted this with starting with a set of. Given a field \(k\) and a polynomial \(f(x)\in k[x]\),. Field Extension Cube Root.
From youvegotthismath.com
10 Square Root and Cube Root Worksheet Free Printable Field Extension Cube Root Interestingly, we can often build a new field from an existing one through a process known as field extension, where additional elements are. I'm trying to find a basis for the field extension q(ζ, 3√2) / q, where ζ is the cube root of unity. It's easy to show that it is a. I attempted this with starting with a. Field Extension Cube Root.
From math.stackexchange.com
abstract algebra Find basis in Extension field Mathematics Stack Field Extension Cube Root Show that this element is algebraic. It's easy to show that it is a. Given a field \(k\) and a polynomial \(f(x)\in k[x]\), how can we find a field extension \(l/k\) containing some root \(\theta\) of \(f(x)\)?. Let fbe the field of rational numbers, and let be a cube root of 2. I attempted this with starting with a set. Field Extension Cube Root.
From www.youtube.com
Q69 Simplify cube root 24 + cube root 81 cube root 192 YouTube Field Extension Cube Root I have the following problem that i am stuck on: Let fbe the field of rational numbers, and let be a cube root of 2. Here's a primitive example of a field extension: I attempted this with starting with a set of. $\mathbb{q}(\sqrt 2) = \{a + b\sqrt 2 \;|\; I'm trying to find a basis for the field extension. Field Extension Cube Root.
From www.mashupmath.com
What is the Cube Root of... — Mashup Math Field Extension Cube Root $\mathbb{q}(\sqrt 2) = \{a + b\sqrt 2 \;|\; Given a field \(k\) and a polynomial \(f(x)\in k[x]\), how can we find a field extension \(l/k\) containing some root \(\theta\) of \(f(x)\)?. The dimension dim f kof kis called the degree of this extension, or the. Here's a primitive example of a field extension: F] of the field extension. Let fbe. Field Extension Cube Root.
From www.chegg.com
Solved 6. a) show that √2 +√3 is algebraic over Q b) Prove Field Extension Cube Root Show that this element is algebraic. Let fbe the field of rational numbers, and let be a cube root of 2. $\mathbb{q}(\sqrt 2) = \{a + b\sqrt 2 \;|\; F] of the field extension. Here's a primitive example of a field extension: I attempted this with starting with a set of. Given a field \(k\) and a polynomial \(f(x)\in k[x]\),. Field Extension Cube Root.
From www.chegg.com
Solved The cube in the figure(Figure 1) contains no net Field Extension Cube Root I attempted this with starting with a set of. I have the following problem that i am stuck on: F] of the field extension. An extension field \(e\) of a field \(f\) is an algebraic extension of \(f\) if every element in \(e\) is algebraic over \(f\text{.}\) if \(e\) is a. $\mathbb{q}(\sqrt 2) = \{a + b\sqrt 2 \;|\; Show. Field Extension Cube Root.
From domainbgr.blogspot.com
Cube Root Function Domain And Range DOMAIN BGR Field Extension Cube Root Here's a primitive example of a field extension: An extension field \(e\) of a field \(f\) is an algebraic extension of \(f\) if every element in \(e\) is algebraic over \(f\text{.}\) if \(e\) is a. I have the following problem that i am stuck on: The dimension dim f kof kis called the degree of this extension, or the. Show. Field Extension Cube Root.
From www.madebyteachers.com
Solving Square and Cube Root Equations Digital SelfChecking Activity Field Extension Cube Root Given a field \(k\) and a polynomial \(f(x)\in k[x]\), how can we find a field extension \(l/k\) containing some root \(\theta\) of \(f(x)\)?. F] of the field extension. An extension field \(e\) of a field \(f\) is an algebraic extension of \(f\) if every element in \(e\) is algebraic over \(f\text{.}\) if \(e\) is a. I have the following problem. Field Extension Cube Root.
From www.youtube.com
CUBE ROOT WITHIN 5 SEC FIND CUBE 3√1771561 CUBE ROOT TRICKS MATH Field Extension Cube Root F] of the field extension. Given a field \(k\) and a polynomial \(f(x)\in k[x]\), how can we find a field extension \(l/k\) containing some root \(\theta\) of \(f(x)\)?. I'm trying to find a basis for the field extension q(ζ, 3√2) / q, where ζ is the cube root of unity. It's easy to show that it is a. Let fbe. Field Extension Cube Root.
From www.youtube.com
Q154 Simplify cube root 2+ cube root 16 cube root 54 Irrational Field Extension Cube Root I attempted this with starting with a set of. Interestingly, we can often build a new field from an existing one through a process known as field extension, where additional elements are. Let fbe the field of rational numbers, and let be a cube root of 2. It's easy to show that it is a. The dimension dim f kof. Field Extension Cube Root.
From www.thestudypath.com
Cube and Cube Roots Chapter 4 Test Paper RS Aggarwal Class 8 Solutions Field Extension Cube Root Interestingly, we can often build a new field from an existing one through a process known as field extension, where additional elements are. The dimension dim f kof kis called the degree of this extension, or the. $\mathbb{q}(\sqrt 2) = \{a + b\sqrt 2 \;|\; Given a field \(k\) and a polynomial \(f(x)\in k[x]\), how can we find a field. Field Extension Cube Root.
From studylib.net
A remark on the computation of cube roots in finite fields Field Extension Cube Root Here's a primitive example of a field extension: Show that this element is algebraic. I have the following problem that i am stuck on: I attempted this with starting with a set of. An extension field \(e\) of a field \(f\) is an algebraic extension of \(f\) if every element in \(e\) is algebraic over \(f\text{.}\) if \(e\) is a.. Field Extension Cube Root.
From www.onlinemathlearning.com
Cubes and Cube Root Worksheet (printable, online, answers, examples) Field Extension Cube Root An extension field \(e\) of a field \(f\) is an algebraic extension of \(f\) if every element in \(e\) is algebraic over \(f\text{.}\) if \(e\) is a. Interestingly, we can often build a new field from an existing one through a process known as field extension, where additional elements are. F] of the field extension. Given a field \(k\) and. Field Extension Cube Root.
From www.template.net
Free Square And Cube Root Chart Download in PDF, Illustrator Field Extension Cube Root An extension field \(e\) of a field \(f\) is an algebraic extension of \(f\) if every element in \(e\) is algebraic over \(f\text{.}\) if \(e\) is a. F] of the field extension. Interestingly, we can often build a new field from an existing one through a process known as field extension, where additional elements are. $\mathbb{q}(\sqrt 2) = \{a +. Field Extension Cube Root.
From www.researchgate.net
Diagram of fields. ω ζN , η ζq are primitive roots of unity. Let p be Field Extension Cube Root Interestingly, we can often build a new field from an existing one through a process known as field extension, where additional elements are. I have the following problem that i am stuck on: Show that this element is algebraic. Here's a primitive example of a field extension: I'm trying to find a basis for the field extension q(ζ, 3√2) /. Field Extension Cube Root.
From testbook.com
How to Calculate Cube Root of 6 with Methods and Solved Examples Field Extension Cube Root Here's a primitive example of a field extension: Show that this element is algebraic. I attempted this with starting with a set of. Given a field \(k\) and a polynomial \(f(x)\in k[x]\), how can we find a field extension \(l/k\) containing some root \(\theta\) of \(f(x)\)?. Interestingly, we can often build a new field from an existing one through a. Field Extension Cube Root.
From freyaburke.z13.web.core.windows.net
Square Root And Cube Root Chart Field Extension Cube Root Here's a primitive example of a field extension: I have the following problem that i am stuck on: I attempted this with starting with a set of. Given a field \(k\) and a polynomial \(f(x)\in k[x]\), how can we find a field extension \(l/k\) containing some root \(\theta\) of \(f(x)\)?. An extension field \(e\) of a field \(f\) is an. Field Extension Cube Root.
From www.youtube.com
Roots of unity in finite fields 4 An equivalent characterization of Field Extension Cube Root Here's a primitive example of a field extension: $\mathbb{q}(\sqrt 2) = \{a + b\sqrt 2 \;|\; I attempted this with starting with a set of. Given a field \(k\) and a polynomial \(f(x)\in k[x]\), how can we find a field extension \(l/k\) containing some root \(\theta\) of \(f(x)\)?. I have the following problem that i am stuck on: F] of. Field Extension Cube Root.
From www.youtube.com
Extension field lecture 11, multiplicity of a root YouTube Field Extension Cube Root Show that this element is algebraic. The dimension dim f kof kis called the degree of this extension, or the. I have the following problem that i am stuck on: Let fbe the field of rational numbers, and let be a cube root of 2. An extension field \(e\) of a field \(f\) is an algebraic extension of \(f\) if. Field Extension Cube Root.
From www.scribd.com
Galois Theory Analyzing Field Extensions, Irreducibility, and the Field Extension Cube Root An extension field \(e\) of a field \(f\) is an algebraic extension of \(f\) if every element in \(e\) is algebraic over \(f\text{.}\) if \(e\) is a. I'm trying to find a basis for the field extension q(ζ, 3√2) / q, where ζ is the cube root of unity. The dimension dim f kof kis called the degree of this. Field Extension Cube Root.
From www.ck12.org
Graphing Cubed Root Functions CK12 Foundation Field Extension Cube Root Interestingly, we can often build a new field from an existing one through a process known as field extension, where additional elements are. I'm trying to find a basis for the field extension q(ζ, 3√2) / q, where ζ is the cube root of unity. An extension field \(e\) of a field \(f\) is an algebraic extension of \(f\) if. Field Extension Cube Root.
From www.onlinemathlearning.com
Perfect Cubes And Cube Roots (video lessons, examples and solutions) Field Extension Cube Root Given a field \(k\) and a polynomial \(f(x)\in k[x]\), how can we find a field extension \(l/k\) containing some root \(\theta\) of \(f(x)\)?. The dimension dim f kof kis called the degree of this extension, or the. Interestingly, we can often build a new field from an existing one through a process known as field extension, where additional elements are.. Field Extension Cube Root.
From www.youtube.com
Complex Number Cube Roots by Template method // Hrb YouTube Field Extension Cube Root The dimension dim f kof kis called the degree of this extension, or the. Interestingly, we can often build a new field from an existing one through a process known as field extension, where additional elements are. Here's a primitive example of a field extension: I attempted this with starting with a set of. It's easy to show that it. Field Extension Cube Root.
From edukatorsclub.com
Cube Root 1 to 30 [PDF Download] Cube Root Field Extension Cube Root Here's a primitive example of a field extension: Given a field \(k\) and a polynomial \(f(x)\in k[x]\), how can we find a field extension \(l/k\) containing some root \(\theta\) of \(f(x)\)?. Show that this element is algebraic. Let fbe the field of rational numbers, and let be a cube root of 2. I'm trying to find a basis for the. Field Extension Cube Root.
From www.teacharesources.com
Cubes, Cube roots, square and square roots A3 Poster • Teacha! Field Extension Cube Root F] of the field extension. Given a field \(k\) and a polynomial \(f(x)\in k[x]\), how can we find a field extension \(l/k\) containing some root \(\theta\) of \(f(x)\)?. I attempted this with starting with a set of. It's easy to show that it is a. Show that this element is algebraic. $\mathbb{q}(\sqrt 2) = \{a + b\sqrt 2 \;|\; Here's. Field Extension Cube Root.
From www.expii.com
Cube Root of Perfect Cubes — Examples & Practice Expii Field Extension Cube Root I have the following problem that i am stuck on: Here's a primitive example of a field extension: Interestingly, we can often build a new field from an existing one through a process known as field extension, where additional elements are. The dimension dim f kof kis called the degree of this extension, or the. Show that this element is. Field Extension Cube Root.
From dfinitus.blogspot.com
Definition Of Cube Root Of Unity DFINITUS Field Extension Cube Root Interestingly, we can often build a new field from an existing one through a process known as field extension, where additional elements are. I have the following problem that i am stuck on: An extension field \(e\) of a field \(f\) is an algebraic extension of \(f\) if every element in \(e\) is algebraic over \(f\text{.}\) if \(e\) is a.. Field Extension Cube Root.