Standard Basis Of R1 . The term standard basis only applies to vector spaces of the form $\bbb f^n$, when every vector is of the form $ (x_1, x_2,., x_n)^t$. Recall that the set \(\left\{ \vec{e}_1, \vec{e}_2, \cdots, \vec{e}_n \right\}\) is called the standard basis of \(\mathbb{r}^n\). What is the standard basis for fields of complex numbers? This basis is often called the \(\textit{standard}\) or \(\textit{canonical basis}\) for \(\re^{n}\). A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. So this set of vectors is a basis for \(\re^{n}\), and \(\dim \re^{n}=n\). There are many possible sets of basis vectors whose spans would create r1 and r2, but the standard basis is the set of elementary vectors,.
from www.chegg.com
So this set of vectors is a basis for \(\re^{n}\), and \(\dim \re^{n}=n\). The term standard basis only applies to vector spaces of the form $\bbb f^n$, when every vector is of the form $ (x_1, x_2,., x_n)^t$. A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. This basis is often called the \(\textit{standard}\) or \(\textit{canonical basis}\) for \(\re^{n}\). Recall that the set \(\left\{ \vec{e}_1, \vec{e}_2, \cdots, \vec{e}_n \right\}\) is called the standard basis of \(\mathbb{r}^n\). There are many possible sets of basis vectors whose spans would create r1 and r2, but the standard basis is the set of elementary vectors,. What is the standard basis for fields of complex numbers?
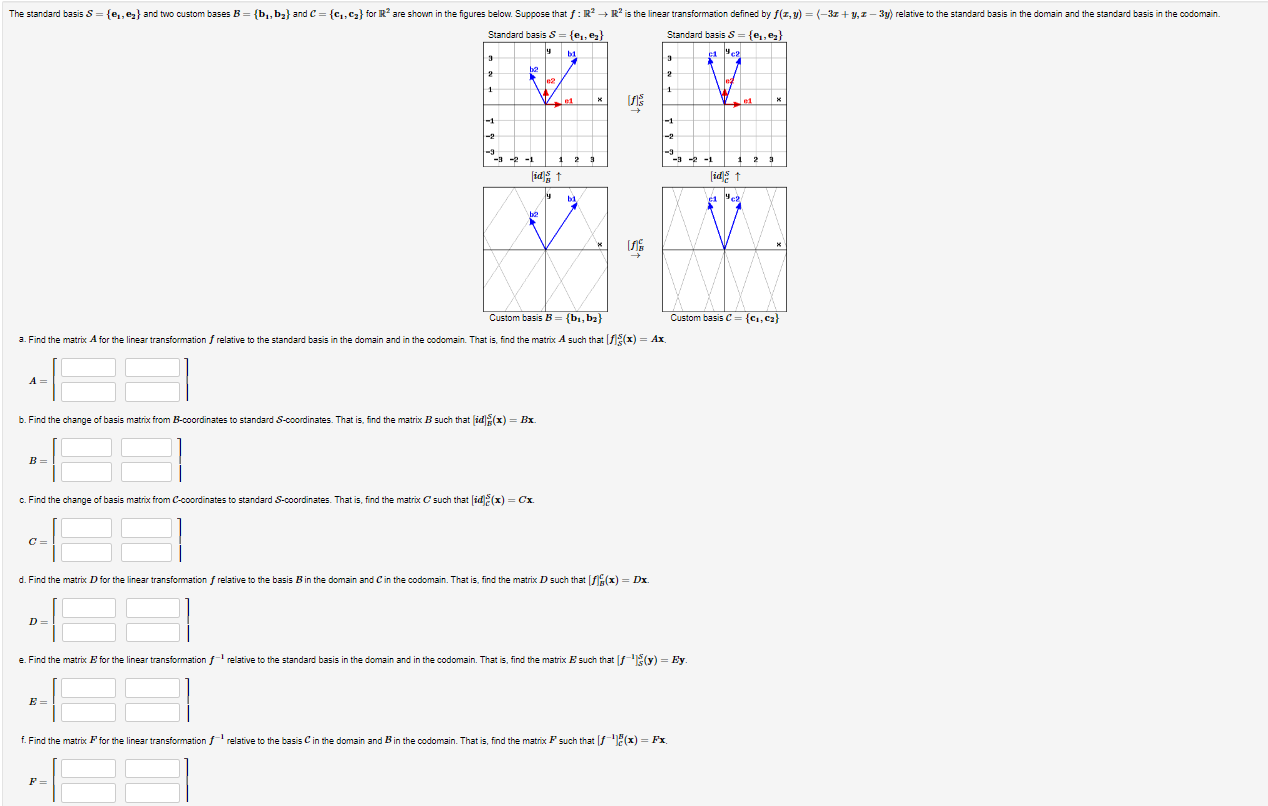
Solved he standard basis S={e1,e2} and two custom bases
Standard Basis Of R1 Recall that the set \(\left\{ \vec{e}_1, \vec{e}_2, \cdots, \vec{e}_n \right\}\) is called the standard basis of \(\mathbb{r}^n\). There are many possible sets of basis vectors whose spans would create r1 and r2, but the standard basis is the set of elementary vectors,. A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. Recall that the set \(\left\{ \vec{e}_1, \vec{e}_2, \cdots, \vec{e}_n \right\}\) is called the standard basis of \(\mathbb{r}^n\). So this set of vectors is a basis for \(\re^{n}\), and \(\dim \re^{n}=n\). The term standard basis only applies to vector spaces of the form $\bbb f^n$, when every vector is of the form $ (x_1, x_2,., x_n)^t$. What is the standard basis for fields of complex numbers? This basis is often called the \(\textit{standard}\) or \(\textit{canonical basis}\) for \(\re^{n}\).
From www.chegg.com
Solved Suppose A is the matrix for TR3→R3 relative to the Standard Basis Of R1 Recall that the set \(\left\{ \vec{e}_1, \vec{e}_2, \cdots, \vec{e}_n \right\}\) is called the standard basis of \(\mathbb{r}^n\). What is the standard basis for fields of complex numbers? The term standard basis only applies to vector spaces of the form $\bbb f^n$, when every vector is of the form $ (x_1, x_2,., x_n)^t$. So this set of vectors is a basis. Standard Basis Of R1.
From guide.openrif.org
National Building Code Parking Requirements Philippines Guides Online Standard Basis Of R1 The term standard basis only applies to vector spaces of the form $\bbb f^n$, when every vector is of the form $ (x_1, x_2,., x_n)^t$. What is the standard basis for fields of complex numbers? A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. This basis is. Standard Basis Of R1.
From www.chegg.com
Solved Suppose TR3→R3 is a transformation whose matrix Standard Basis Of R1 Recall that the set \(\left\{ \vec{e}_1, \vec{e}_2, \cdots, \vec{e}_n \right\}\) is called the standard basis of \(\mathbb{r}^n\). What is the standard basis for fields of complex numbers? There are many possible sets of basis vectors whose spans would create r1 and r2, but the standard basis is the set of elementary vectors,. So this set of vectors is a basis. Standard Basis Of R1.
From fresherscamp.com
R1 RCM Hiring 2023 For Trainee Software Engineer Noida FreshersCamp Standard Basis Of R1 What is the standard basis for fields of complex numbers? This basis is often called the \(\textit{standard}\) or \(\textit{canonical basis}\) for \(\re^{n}\). There are many possible sets of basis vectors whose spans would create r1 and r2, but the standard basis is the set of elementary vectors,. Recall that the set \(\left\{ \vec{e}_1, \vec{e}_2, \cdots, \vec{e}_n \right\}\) is called the. Standard Basis Of R1.
From www.chegg.com
Solved The standard basis S={e1,e2} and a custom basis Standard Basis Of R1 So this set of vectors is a basis for \(\re^{n}\), and \(\dim \re^{n}=n\). What is the standard basis for fields of complex numbers? Recall that the set \(\left\{ \vec{e}_1, \vec{e}_2, \cdots, \vec{e}_n \right\}\) is called the standard basis of \(\mathbb{r}^n\). This basis is often called the \(\textit{standard}\) or \(\textit{canonical basis}\) for \(\re^{n}\). There are many possible sets of basis vectors. Standard Basis Of R1.
From slideserve.com
PPT Finding Eigenvalues and Eigenvectors PowerPoint Presentation ID Standard Basis Of R1 The term standard basis only applies to vector spaces of the form $\bbb f^n$, when every vector is of the form $ (x_1, x_2,., x_n)^t$. So this set of vectors is a basis for \(\re^{n}\), and \(\dim \re^{n}=n\). There are many possible sets of basis vectors whose spans would create r1 and r2, but the standard basis is the set. Standard Basis Of R1.
From www.youtube.com
The Standard Basis of a General Linear Transformation YouTube Standard Basis Of R1 This basis is often called the \(\textit{standard}\) or \(\textit{canonical basis}\) for \(\re^{n}\). The term standard basis only applies to vector spaces of the form $\bbb f^n$, when every vector is of the form $ (x_1, x_2,., x_n)^t$. So this set of vectors is a basis for \(\re^{n}\), and \(\dim \re^{n}=n\). Recall that the set \(\left\{ \vec{e}_1, \vec{e}_2, \cdots, \vec{e}_n \right\}\). Standard Basis Of R1.
From www.scribd.com
Basis of Estimate R1 PDF Standard Basis Of R1 There are many possible sets of basis vectors whose spans would create r1 and r2, but the standard basis is the set of elementary vectors,. What is the standard basis for fields of complex numbers? The term standard basis only applies to vector spaces of the form $\bbb f^n$, when every vector is of the form $ (x_1, x_2,., x_n)^t$.. Standard Basis Of R1.
From zief0002.github.io
Chapter 16 Basis Vectors and Matrices Matrix Algebra for Educational Standard Basis Of R1 There are many possible sets of basis vectors whose spans would create r1 and r2, but the standard basis is the set of elementary vectors,. This basis is often called the \(\textit{standard}\) or \(\textit{canonical basis}\) for \(\re^{n}\). What is the standard basis for fields of complex numbers? So this set of vectors is a basis for \(\re^{n}\), and \(\dim \re^{n}=n\).. Standard Basis Of R1.
From www.studocu.com
File 5 Definition with examples of bases 4 Basis and Dimension Standard Basis Of R1 The term standard basis only applies to vector spaces of the form $\bbb f^n$, when every vector is of the form $ (x_1, x_2,., x_n)^t$. Recall that the set \(\left\{ \vec{e}_1, \vec{e}_2, \cdots, \vec{e}_n \right\}\) is called the standard basis of \(\mathbb{r}^n\). So this set of vectors is a basis for \(\re^{n}\), and \(\dim \re^{n}=n\). What is the standard basis. Standard Basis Of R1.
From www.numerade.com
Find a standard basis vector for R^{3} that can b… Standard Basis Of R1 The term standard basis only applies to vector spaces of the form $\bbb f^n$, when every vector is of the form $ (x_1, x_2,., x_n)^t$. What is the standard basis for fields of complex numbers? This basis is often called the \(\textit{standard}\) or \(\textit{canonical basis}\) for \(\re^{n}\). So this set of vectors is a basis for \(\re^{n}\), and \(\dim \re^{n}=n\).. Standard Basis Of R1.
From www.chegg.com
Solved Suppose A is the matrix for TR3→R3 relative to the Standard Basis Of R1 There are many possible sets of basis vectors whose spans would create r1 and r2, but the standard basis is the set of elementary vectors,. So this set of vectors is a basis for \(\re^{n}\), and \(\dim \re^{n}=n\). A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single.. Standard Basis Of R1.
From www.numerade.com
SOLVED QUESTICN 2 Lets(0) ()() € Is S is linearly independent Give Standard Basis Of R1 The term standard basis only applies to vector spaces of the form $\bbb f^n$, when every vector is of the form $ (x_1, x_2,., x_n)^t$. A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. What is the standard basis for fields of complex numbers? There are many. Standard Basis Of R1.
From www.chegg.com
Solved The standard basis S={e1,e2} and two custom bases Standard Basis Of R1 A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. This basis is often called the \(\textit{standard}\) or \(\textit{canonical basis}\) for \(\re^{n}\). What is the standard basis for fields of complex numbers? There are many possible sets of basis vectors whose spans would create r1 and r2, but. Standard Basis Of R1.
From zief0002.github.io
Chapter 16 Basis Vectors and Matrices Matrix Algebra for Educational Standard Basis Of R1 This basis is often called the \(\textit{standard}\) or \(\textit{canonical basis}\) for \(\re^{n}\). Recall that the set \(\left\{ \vec{e}_1, \vec{e}_2, \cdots, \vec{e}_n \right\}\) is called the standard basis of \(\mathbb{r}^n\). What is the standard basis for fields of complex numbers? The term standard basis only applies to vector spaces of the form $\bbb f^n$, when every vector is of the form. Standard Basis Of R1.
From www.chegg.com
Solved find the change of coordinates matrix from the Standard Basis Of R1 A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. There are many possible sets of basis vectors whose spans would create r1 and r2, but the standard basis is the set of elementary vectors,. Recall that the set \(\left\{ \vec{e}_1, \vec{e}_2, \cdots, \vec{e}_n \right\}\) is called the. Standard Basis Of R1.
From exoyzowaw.blob.core.windows.net
Standard Basis Vs Indemnity Basis at Karen Kim blog Standard Basis Of R1 Recall that the set \(\left\{ \vec{e}_1, \vec{e}_2, \cdots, \vec{e}_n \right\}\) is called the standard basis of \(\mathbb{r}^n\). There are many possible sets of basis vectors whose spans would create r1 and r2, but the standard basis is the set of elementary vectors,. This basis is often called the \(\textit{standard}\) or \(\textit{canonical basis}\) for \(\re^{n}\). So this set of vectors is. Standard Basis Of R1.
From www.chegg.com
Solved The standard basis S={e1,e2} and a custom basis Standard Basis Of R1 What is the standard basis for fields of complex numbers? This basis is often called the \(\textit{standard}\) or \(\textit{canonical basis}\) for \(\re^{n}\). So this set of vectors is a basis for \(\re^{n}\), and \(\dim \re^{n}=n\). The term standard basis only applies to vector spaces of the form $\bbb f^n$, when every vector is of the form $ (x_1, x_2,., x_n)^t$.. Standard Basis Of R1.
From www.slideserve.com
PPT 5.4 Basis And Dimension PowerPoint Presentation, free download Standard Basis Of R1 So this set of vectors is a basis for \(\re^{n}\), and \(\dim \re^{n}=n\). The term standard basis only applies to vector spaces of the form $\bbb f^n$, when every vector is of the form $ (x_1, x_2,., x_n)^t$. Recall that the set \(\left\{ \vec{e}_1, \vec{e}_2, \cdots, \vec{e}_n \right\}\) is called the standard basis of \(\mathbb{r}^n\). What is the standard basis. Standard Basis Of R1.
From www.scribd.com
1416MCDBS101_MECHANICAL DESIGN BASIS_R1 PDF Pipe (Fluid Standard Basis Of R1 There are many possible sets of basis vectors whose spans would create r1 and r2, but the standard basis is the set of elementary vectors,. What is the standard basis for fields of complex numbers? A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. Recall that the. Standard Basis Of R1.
From www.numerade.com
SOLVED (1 point) The set [ ][ ][ ] is called the standard basis Standard Basis Of R1 There are many possible sets of basis vectors whose spans would create r1 and r2, but the standard basis is the set of elementary vectors,. Recall that the set \(\left\{ \vec{e}_1, \vec{e}_2, \cdots, \vec{e}_n \right\}\) is called the standard basis of \(\mathbb{r}^n\). So this set of vectors is a basis for \(\re^{n}\), and \(\dim \re^{n}=n\). What is the standard basis. Standard Basis Of R1.
From www.chegg.com
(2 points) The standard basis S={e1,e2} and two Standard Basis Of R1 So this set of vectors is a basis for \(\re^{n}\), and \(\dim \re^{n}=n\). Recall that the set \(\left\{ \vec{e}_1, \vec{e}_2, \cdots, \vec{e}_n \right\}\) is called the standard basis of \(\mathbb{r}^n\). There are many possible sets of basis vectors whose spans would create r1 and r2, but the standard basis is the set of elementary vectors,. What is the standard basis. Standard Basis Of R1.
From www.motorradonline.de
Fahrbericht Yamaha R1 GYTR für 2023 Standard Basis Of R1 So this set of vectors is a basis for \(\re^{n}\), and \(\dim \re^{n}=n\). This basis is often called the \(\textit{standard}\) or \(\textit{canonical basis}\) for \(\re^{n}\). A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. There are many possible sets of basis vectors whose spans would create r1. Standard Basis Of R1.
From giorfikol.blob.core.windows.net
Standard Basis Linear Transformation at Ina Tran blog Standard Basis Of R1 This basis is often called the \(\textit{standard}\) or \(\textit{canonical basis}\) for \(\re^{n}\). Recall that the set \(\left\{ \vec{e}_1, \vec{e}_2, \cdots, \vec{e}_n \right\}\) is called the standard basis of \(\mathbb{r}^n\). What is the standard basis for fields of complex numbers? The term standard basis only applies to vector spaces of the form $\bbb f^n$, when every vector is of the form. Standard Basis Of R1.
From www.slideserve.com
PPT Geometry of R 2 and R 3 PowerPoint Presentation, free download Standard Basis Of R1 This basis is often called the \(\textit{standard}\) or \(\textit{canonical basis}\) for \(\re^{n}\). What is the standard basis for fields of complex numbers? A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. There are many possible sets of basis vectors whose spans would create r1 and r2, but. Standard Basis Of R1.
From www.chegg.com
Solved The standard basis S={e1,e2} and two custom bases Standard Basis Of R1 A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. The term standard basis only applies to vector spaces of the form $\bbb f^n$, when every vector is of the form $ (x_1, x_2,., x_n)^t$. So this set of vectors is a basis for \(\re^{n}\), and \(\dim \re^{n}=n\).. Standard Basis Of R1.
From www.chegg.com
Solved Consider the linear transformation T Rn → Rn whose Standard Basis Of R1 What is the standard basis for fields of complex numbers? This basis is often called the \(\textit{standard}\) or \(\textit{canonical basis}\) for \(\re^{n}\). Recall that the set \(\left\{ \vec{e}_1, \vec{e}_2, \cdots, \vec{e}_n \right\}\) is called the standard basis of \(\mathbb{r}^n\). So this set of vectors is a basis for \(\re^{n}\), and \(\dim \re^{n}=n\). There are many possible sets of basis vectors. Standard Basis Of R1.
From glints.com
Jobs at R1 Skincare, Singapore, January 2024 Glints Standard Basis Of R1 The term standard basis only applies to vector spaces of the form $\bbb f^n$, when every vector is of the form $ (x_1, x_2,., x_n)^t$. A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. Recall that the set \(\left\{ \vec{e}_1, \vec{e}_2, \cdots, \vec{e}_n \right\}\) is called the. Standard Basis Of R1.
From www.youtube.com
Change of Basis (using coordinate isomorphism) YouTube Standard Basis Of R1 So this set of vectors is a basis for \(\re^{n}\), and \(\dim \re^{n}=n\). A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. What is the standard basis for fields of complex numbers? There are many possible sets of basis vectors whose spans would create r1 and r2,. Standard Basis Of R1.
From www.solutionspile.com
[Solved] The standard basis S={e1,e2} and a custom basis B Standard Basis Of R1 The term standard basis only applies to vector spaces of the form $\bbb f^n$, when every vector is of the form $ (x_1, x_2,., x_n)^t$. What is the standard basis for fields of complex numbers? Recall that the set \(\left\{ \vec{e}_1, \vec{e}_2, \cdots, \vec{e}_n \right\}\) is called the standard basis of \(\mathbb{r}^n\). So this set of vectors is a basis. Standard Basis Of R1.
From www.youtube.com
Finding a Standard Matrix Using the Standard Basis YouTube Standard Basis Of R1 Recall that the set \(\left\{ \vec{e}_1, \vec{e}_2, \cdots, \vec{e}_n \right\}\) is called the standard basis of \(\mathbb{r}^n\). There are many possible sets of basis vectors whose spans would create r1 and r2, but the standard basis is the set of elementary vectors,. A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis. Standard Basis Of R1.
From www.chegg.com
Solved he standard basis S={e1,e2} and two custom bases Standard Basis Of R1 There are many possible sets of basis vectors whose spans would create r1 and r2, but the standard basis is the set of elementary vectors,. What is the standard basis for fields of complex numbers? A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. This basis is. Standard Basis Of R1.
From www.chegg.com
Solved Suppose A is the matrix for T R3 → R3 relative to Standard Basis Of R1 This basis is often called the \(\textit{standard}\) or \(\textit{canonical basis}\) for \(\re^{n}\). Recall that the set \(\left\{ \vec{e}_1, \vec{e}_2, \cdots, \vec{e}_n \right\}\) is called the standard basis of \(\mathbb{r}^n\). So this set of vectors is a basis for \(\re^{n}\), and \(\dim \re^{n}=n\). A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis. Standard Basis Of R1.
From www.numerade.com
SOLVEDFind the matrix of the given linear transformation T with Standard Basis Of R1 Recall that the set \(\left\{ \vec{e}_1, \vec{e}_2, \cdots, \vec{e}_n \right\}\) is called the standard basis of \(\mathbb{r}^n\). So this set of vectors is a basis for \(\re^{n}\), and \(\dim \re^{n}=n\). There are many possible sets of basis vectors whose spans would create r1 and r2, but the standard basis is the set of elementary vectors,. What is the standard basis. Standard Basis Of R1.
From www.chegg.com
Solved Suppose A is the matrix for TR3→R3 relative to the Standard Basis Of R1 A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. So this set of vectors is a basis for \(\re^{n}\), and \(\dim \re^{n}=n\). This basis is often called the \(\textit{standard}\) or \(\textit{canonical basis}\) for \(\re^{n}\). What is the standard basis for fields of complex numbers? Recall that the. Standard Basis Of R1.