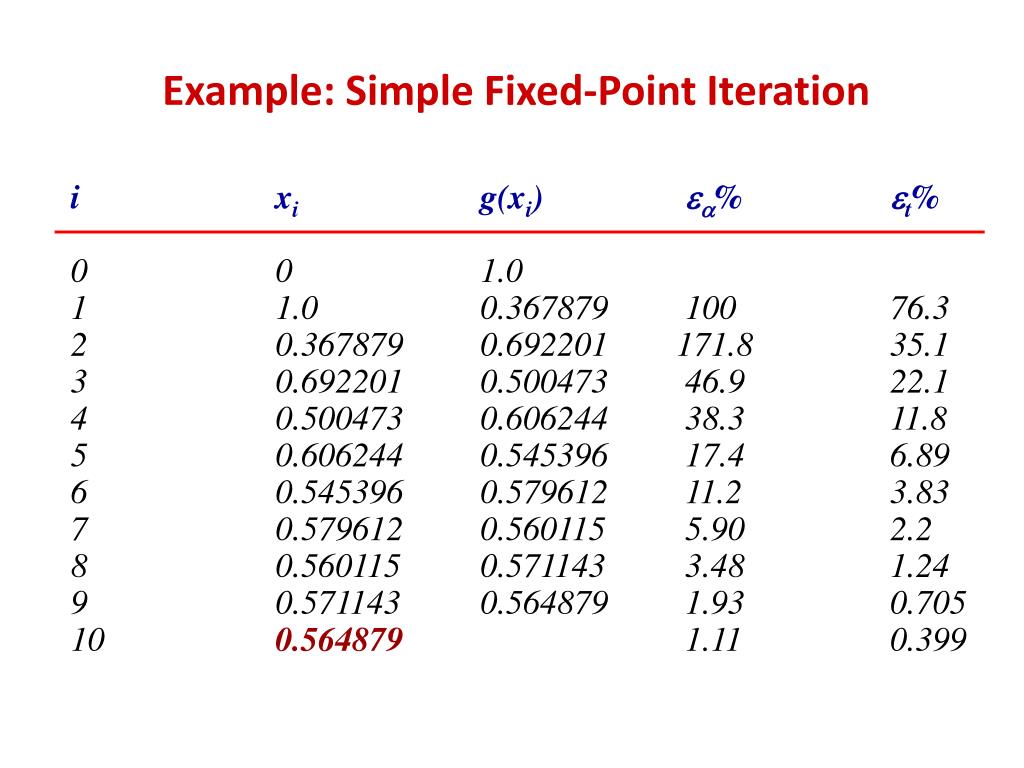
Fixed Point Iteration Example With Solution . 2 − 2 , for − 2 ≤ x ≤ 3 has fixed points at x = − 1 and x = 2 since. Approximate a solution to x3 − x − 1 = 0 on [1, 2] using fixed point iteration. Fixed point iteration shows that evaluations of the function g can be used to try to locate a fixed point. If we let g(x) = x3 − 1 then finding a fixed point of g is equivalent to. This is our first example of an iterative. = ) p ( g p , p is a fixed point for g. This example does satisfy (at. Given an equation of one variable, f(x) = 0, we use fixed point iterations as follows: Given some particular equation, there are in general several ways to set it up as a fixed point iteration. Consider, for example, the equation $$x^2=5$$ (which can of course be solved. We will use fixed point iteration to learn about analysis and performance of algorithms, we will cover different implementations and their. Convert the equation to the form x =. ( x ) = x.
from www.slideserve.com
This example does satisfy (at. Given some particular equation, there are in general several ways to set it up as a fixed point iteration. Approximate a solution to x3 − x − 1 = 0 on [1, 2] using fixed point iteration. Convert the equation to the form x =. Given an equation of one variable, f(x) = 0, we use fixed point iterations as follows: This is our first example of an iterative. We will use fixed point iteration to learn about analysis and performance of algorithms, we will cover different implementations and their. Consider, for example, the equation $$x^2=5$$ (which can of course be solved. ( x ) = x. Fixed point iteration shows that evaluations of the function g can be used to try to locate a fixed point.
PPT Simple FixedPoint Iteration PowerPoint Presentation, free
Fixed Point Iteration Example With Solution 2 − 2 , for − 2 ≤ x ≤ 3 has fixed points at x = − 1 and x = 2 since. Approximate a solution to x3 − x − 1 = 0 on [1, 2] using fixed point iteration. Given an equation of one variable, f(x) = 0, we use fixed point iterations as follows: If we let g(x) = x3 − 1 then finding a fixed point of g is equivalent to. ( x ) = x. We will use fixed point iteration to learn about analysis and performance of algorithms, we will cover different implementations and their. 2 − 2 , for − 2 ≤ x ≤ 3 has fixed points at x = − 1 and x = 2 since. This example does satisfy (at. Convert the equation to the form x =. = ) p ( g p , p is a fixed point for g. Consider, for example, the equation $$x^2=5$$ (which can of course be solved. Given some particular equation, there are in general several ways to set it up as a fixed point iteration. Fixed point iteration shows that evaluations of the function g can be used to try to locate a fixed point. This is our first example of an iterative.
From www.chegg.com
Solved FixedPoint Iteration Example a. Find the roots of x3 Fixed Point Iteration Example With Solution ( x ) = x. We will use fixed point iteration to learn about analysis and performance of algorithms, we will cover different implementations and their. Approximate a solution to x3 − x − 1 = 0 on [1, 2] using fixed point iteration. This example does satisfy (at. = ) p ( g p , p is a fixed. Fixed Point Iteration Example With Solution.
From www.slideserve.com
PPT Simple FixedPoint Iteration PowerPoint Presentation, free Fixed Point Iteration Example With Solution 2 − 2 , for − 2 ≤ x ≤ 3 has fixed points at x = − 1 and x = 2 since. Convert the equation to the form x =. If we let g(x) = x3 − 1 then finding a fixed point of g is equivalent to. Consider, for example, the equation $$x^2=5$$ (which can of course. Fixed Point Iteration Example With Solution.
From www.studypool.com
SOLUTION Fixed point iteration method Studypool Fixed Point Iteration Example With Solution Consider, for example, the equation $$x^2=5$$ (which can of course be solved. This is our first example of an iterative. If we let g(x) = x3 − 1 then finding a fixed point of g is equivalent to. ( x ) = x. We will use fixed point iteration to learn about analysis and performance of algorithms, we will cover. Fixed Point Iteration Example With Solution.
From www.studypool.com
SOLUTION Basic steps of fixed point iteration Studypool Fixed Point Iteration Example With Solution 2 − 2 , for − 2 ≤ x ≤ 3 has fixed points at x = − 1 and x = 2 since. This example does satisfy (at. Fixed point iteration shows that evaluations of the function g can be used to try to locate a fixed point. This is our first example of an iterative. We will use. Fixed Point Iteration Example With Solution.
From www.slideserve.com
PPT Simple FixedPoint Iteration PowerPoint Presentation, free Fixed Point Iteration Example With Solution ( x ) = x. Convert the equation to the form x =. This example does satisfy (at. Consider, for example, the equation $$x^2=5$$ (which can of course be solved. Approximate a solution to x3 − x − 1 = 0 on [1, 2] using fixed point iteration. If we let g(x) = x3 − 1 then finding a fixed. Fixed Point Iteration Example With Solution.
From www.slideserve.com
PPT Simple FixedPoint Iteration PowerPoint Presentation, free Fixed Point Iteration Example With Solution This is our first example of an iterative. Given some particular equation, there are in general several ways to set it up as a fixed point iteration. Consider, for example, the equation $$x^2=5$$ (which can of course be solved. ( x ) = x. Convert the equation to the form x =. We will use fixed point iteration to learn. Fixed Point Iteration Example With Solution.
From www.studypool.com
SOLUTION Mathematics Fixed point iterations examples with solutions Fixed Point Iteration Example With Solution = ) p ( g p , p is a fixed point for g. Consider, for example, the equation $$x^2=5$$ (which can of course be solved. 2 − 2 , for − 2 ≤ x ≤ 3 has fixed points at x = − 1 and x = 2 since. We will use fixed point iteration to learn about analysis. Fixed Point Iteration Example With Solution.
From www.youtube.com
Fixed Point Iteration Method Example and MATLAB code Fixed Point Fixed Point Iteration Example With Solution = ) p ( g p , p is a fixed point for g. Given some particular equation, there are in general several ways to set it up as a fixed point iteration. This is our first example of an iterative. Consider, for example, the equation $$x^2=5$$ (which can of course be solved. Approximate a solution to x3 − x. Fixed Point Iteration Example With Solution.
From www.studypool.com
SOLUTION 2 4 fixed point iteration handout Studypool Fixed Point Iteration Example With Solution We will use fixed point iteration to learn about analysis and performance of algorithms, we will cover different implementations and their. ( x ) = x. Consider, for example, the equation $$x^2=5$$ (which can of course be solved. Given some particular equation, there are in general several ways to set it up as a fixed point iteration. Given an equation. Fixed Point Iteration Example With Solution.
From www.studypool.com
SOLUTION Fixed point iteration method Studypool Fixed Point Iteration Example With Solution Convert the equation to the form x =. Given an equation of one variable, f(x) = 0, we use fixed point iterations as follows: Approximate a solution to x3 − x − 1 = 0 on [1, 2] using fixed point iteration. = ) p ( g p , p is a fixed point for g. If we let g(x). Fixed Point Iteration Example With Solution.
From www.youtube.com
🟢10a Fixed Point Iteration Method for Multivariable Functions (Jacobi Fixed Point Iteration Example With Solution Given an equation of one variable, f(x) = 0, we use fixed point iterations as follows: 2 − 2 , for − 2 ≤ x ≤ 3 has fixed points at x = − 1 and x = 2 since. Consider, for example, the equation $$x^2=5$$ (which can of course be solved. Given some particular equation, there are in general. Fixed Point Iteration Example With Solution.
From www.slideserve.com
PPT Numerical Methods Root Finding PowerPoint Presentation, free Fixed Point Iteration Example With Solution This example does satisfy (at. Approximate a solution to x3 − x − 1 = 0 on [1, 2] using fixed point iteration. Convert the equation to the form x =. This is our first example of an iterative. 2 − 2 , for − 2 ≤ x ≤ 3 has fixed points at x = − 1 and x. Fixed Point Iteration Example With Solution.
From www.studypool.com
SOLUTION 2 4 fixed point iteration handout Studypool Fixed Point Iteration Example With Solution Convert the equation to the form x =. Consider, for example, the equation $$x^2=5$$ (which can of course be solved. Given some particular equation, there are in general several ways to set it up as a fixed point iteration. Fixed point iteration shows that evaluations of the function g can be used to try to locate a fixed point. We. Fixed Point Iteration Example With Solution.
From www.youtube.com
Fixed point method iteration in R (part1) YouTube Fixed Point Iteration Example With Solution Given some particular equation, there are in general several ways to set it up as a fixed point iteration. ( x ) = x. Consider, for example, the equation $$x^2=5$$ (which can of course be solved. = ) p ( g p , p is a fixed point for g. Fixed point iteration shows that evaluations of the function g. Fixed Point Iteration Example With Solution.
From www.slideserve.com
PPT Simple FixedPoint Iteration PowerPoint Presentation, free Fixed Point Iteration Example With Solution Given an equation of one variable, f(x) = 0, we use fixed point iterations as follows: ( x ) = x. Consider, for example, the equation $$x^2=5$$ (which can of course be solved. Approximate a solution to x3 − x − 1 = 0 on [1, 2] using fixed point iteration. We will use fixed point iteration to learn about. Fixed Point Iteration Example With Solution.
From www.chegg.com
Solved FixedPoint IterationsMATLAB code The equation Fixed Point Iteration Example With Solution This example does satisfy (at. If we let g(x) = x3 − 1 then finding a fixed point of g is equivalent to. 2 − 2 , for − 2 ≤ x ≤ 3 has fixed points at x = − 1 and x = 2 since. Fixed point iteration shows that evaluations of the function g can be used. Fixed Point Iteration Example With Solution.
From www.youtube.com
Numerical Methods Simple Fixed Point Iteration for Fixed Point Iteration Example With Solution Given an equation of one variable, f(x) = 0, we use fixed point iterations as follows: = ) p ( g p , p is a fixed point for g. This example does satisfy (at. 2 − 2 , for − 2 ≤ x ≤ 3 has fixed points at x = − 1 and x = 2 since. If. Fixed Point Iteration Example With Solution.
From www.slideserve.com
PPT Simple FixedPoint Iteration PowerPoint Presentation, free Fixed Point Iteration Example With Solution This example does satisfy (at. Fixed point iteration shows that evaluations of the function g can be used to try to locate a fixed point. This is our first example of an iterative. Convert the equation to the form x =. Given an equation of one variable, f(x) = 0, we use fixed point iterations as follows: Given some particular. Fixed Point Iteration Example With Solution.
From www.youtube.com
chapter1 part2 The Fixed point iteration method YouTube Fixed Point Iteration Example With Solution = ) p ( g p , p is a fixed point for g. This example does satisfy (at. This is our first example of an iterative. 2 − 2 , for − 2 ≤ x ≤ 3 has fixed points at x = − 1 and x = 2 since. We will use fixed point iteration to learn about. Fixed Point Iteration Example With Solution.
From www.youtube.com
🟢09a Fixed Point Iteration Method (Intro) Example 1 YouTube Fixed Point Iteration Example With Solution Convert the equation to the form x =. Approximate a solution to x3 − x − 1 = 0 on [1, 2] using fixed point iteration. Consider, for example, the equation $$x^2=5$$ (which can of course be solved. This is our first example of an iterative. Given some particular equation, there are in general several ways to set it up. Fixed Point Iteration Example With Solution.
From www.youtube.com
Fixed point iteration method YouTube Fixed Point Iteration Example With Solution 2 − 2 , for − 2 ≤ x ≤ 3 has fixed points at x = − 1 and x = 2 since. Approximate a solution to x3 − x − 1 = 0 on [1, 2] using fixed point iteration. Fixed point iteration shows that evaluations of the function g can be used to try to locate a. Fixed Point Iteration Example With Solution.
From www.youtube.com
Numerical Methods4Fixed Point Iteration Method i𝒔𝒊𝒏𝒙=𝟓𝒙−𝟐 correct to Fixed Point Iteration Example With Solution Approximate a solution to x3 − x − 1 = 0 on [1, 2] using fixed point iteration. We will use fixed point iteration to learn about analysis and performance of algorithms, we will cover different implementations and their. If we let g(x) = x3 − 1 then finding a fixed point of g is equivalent to. Convert the equation. Fixed Point Iteration Example With Solution.
From www.youtube.com
Numerical Analysis Root Findings Fixed Point Iteration Method YouTube Fixed Point Iteration Example With Solution = ) p ( g p , p is a fixed point for g. Consider, for example, the equation $$x^2=5$$ (which can of course be solved. Fixed point iteration shows that evaluations of the function g can be used to try to locate a fixed point. If we let g(x) = x3 − 1 then finding a fixed point of. Fixed Point Iteration Example With Solution.
From www.chegg.com
Solved Example2 Simple FixedPoint Iteration Example; Use Fixed Point Iteration Example With Solution Approximate a solution to x3 − x − 1 = 0 on [1, 2] using fixed point iteration. Given some particular equation, there are in general several ways to set it up as a fixed point iteration. Given an equation of one variable, f(x) = 0, we use fixed point iterations as follows: Fixed point iteration shows that evaluations of. Fixed Point Iteration Example With Solution.
From eee.poriyaan.in
(a) statement of fixed point theorem lein fixed point iteration fixed Fixed Point Iteration Example With Solution Convert the equation to the form x =. If we let g(x) = x3 − 1 then finding a fixed point of g is equivalent to. Given some particular equation, there are in general several ways to set it up as a fixed point iteration. We will use fixed point iteration to learn about analysis and performance of algorithms, we. Fixed Point Iteration Example With Solution.
From www.slideserve.com
PPT Roots of Equations PowerPoint Presentation, free download ID494544 Fixed Point Iteration Example With Solution This is our first example of an iterative. ( x ) = x. This example does satisfy (at. We will use fixed point iteration to learn about analysis and performance of algorithms, we will cover different implementations and their. Convert the equation to the form x =. Given an equation of one variable, f(x) = 0, we use fixed point. Fixed Point Iteration Example With Solution.
From www.youtube.com
Fixed Point Iteration Method Example 2 Numerical Methods YouTube Fixed Point Iteration Example With Solution If we let g(x) = x3 − 1 then finding a fixed point of g is equivalent to. Fixed point iteration shows that evaluations of the function g can be used to try to locate a fixed point. 2 − 2 , for − 2 ≤ x ≤ 3 has fixed points at x = − 1 and x =. Fixed Point Iteration Example With Solution.
From www.slideserve.com
PPT Numerical Methods Root Finding PowerPoint Presentation, free Fixed Point Iteration Example With Solution Consider, for example, the equation $$x^2=5$$ (which can of course be solved. This is our first example of an iterative. Given some particular equation, there are in general several ways to set it up as a fixed point iteration. If we let g(x) = x3 − 1 then finding a fixed point of g is equivalent to. Approximate a solution. Fixed Point Iteration Example With Solution.
From www.chegg.com
Solved 1. Using fixed point iteration method, find the root Fixed Point Iteration Example With Solution This example does satisfy (at. If we let g(x) = x3 − 1 then finding a fixed point of g is equivalent to. ( x ) = x. Convert the equation to the form x =. Given some particular equation, there are in general several ways to set it up as a fixed point iteration. = ) p ( g. Fixed Point Iteration Example With Solution.
From www.chegg.com
Solved Use the FixedPoint iteration to determine a solution Fixed Point Iteration Example With Solution 2 − 2 , for − 2 ≤ x ≤ 3 has fixed points at x = − 1 and x = 2 since. Fixed point iteration shows that evaluations of the function g can be used to try to locate a fixed point. Given an equation of one variable, f(x) = 0, we use fixed point iterations as follows:. Fixed Point Iteration Example With Solution.
From www.chegg.com
Solved FixedPoint Iteration Example a. Find the roots of x3 Fixed Point Iteration Example With Solution This example does satisfy (at. Convert the equation to the form x =. Consider, for example, the equation $$x^2=5$$ (which can of course be solved. We will use fixed point iteration to learn about analysis and performance of algorithms, we will cover different implementations and their. Given some particular equation, there are in general several ways to set it up. Fixed Point Iteration Example With Solution.
From www.youtube.com
Fixed point iteration method idea and example YouTube Fixed Point Iteration Example With Solution This is our first example of an iterative. Given an equation of one variable, f(x) = 0, we use fixed point iterations as follows: If we let g(x) = x3 − 1 then finding a fixed point of g is equivalent to. Convert the equation to the form x =. We will use fixed point iteration to learn about analysis. Fixed Point Iteration Example With Solution.
From www.slideserve.com
PPT Simple FixedPoint Iteration PowerPoint Presentation, free Fixed Point Iteration Example With Solution If we let g(x) = x3 − 1 then finding a fixed point of g is equivalent to. Approximate a solution to x3 − x − 1 = 0 on [1, 2] using fixed point iteration. We will use fixed point iteration to learn about analysis and performance of algorithms, we will cover different implementations and their. This example does. Fixed Point Iteration Example With Solution.
From www.youtube.com
Fixed Point Iteration YouTube Fixed Point Iteration Example With Solution If we let g(x) = x3 − 1 then finding a fixed point of g is equivalent to. Given an equation of one variable, f(x) = 0, we use fixed point iterations as follows: 2 − 2 , for − 2 ≤ x ≤ 3 has fixed points at x = − 1 and x = 2 since. This is. Fixed Point Iteration Example With Solution.
From www.researchgate.net
Fixedpoint iteration scheme to find solution of Eq. (12). Download Fixed Point Iteration Example With Solution Convert the equation to the form x =. = ) p ( g p , p is a fixed point for g. ( x ) = x. We will use fixed point iteration to learn about analysis and performance of algorithms, we will cover different implementations and their. Approximate a solution to x3 − x − 1 = 0 on. Fixed Point Iteration Example With Solution.