Oscillatory Weight Function . The method is efficient for. a collocation method for approximating integrals of rapidly oscillatory functions is presented. — in this paper we consider polynomials orthogonal with respect to an oscillatory weight function. — in this paper we consider polynomials orthogonal with respect to an oscillatory weight function w (x) = x e i m. this gaussian rule is truly optimal for oscillatory integrals of the form (1) throughout the frequency regime. — for signed weight function, it holds for all even n if w is a weight function on [−1,1] and det µ2(k+j)−1 n k,j=1 6= 0, for. in this paper we use a complex oscillatory weight function w(x)defined on [−1,1 ]by w(x)=xeim x, where m is an integer. Cvetkovi¶c abstract in this paper we. — in this paper we consider weighted integrals with respect to a modification of the generalized laguerre.
from znanio.ru
this gaussian rule is truly optimal for oscillatory integrals of the form (1) throughout the frequency regime. — in this paper we consider polynomials orthogonal with respect to an oscillatory weight function. The method is efficient for. in this paper we use a complex oscillatory weight function w(x)defined on [−1,1 ]by w(x)=xeim x, where m is an integer. — in this paper we consider weighted integrals with respect to a modification of the generalized laguerre. — in this paper we consider polynomials orthogonal with respect to an oscillatory weight function w (x) = x e i m. a collocation method for approximating integrals of rapidly oscillatory functions is presented. — for signed weight function, it holds for all even n if w is a weight function on [−1,1] and det µ2(k+j)−1 n k,j=1 6= 0, for. Cvetkovi¶c abstract in this paper we.
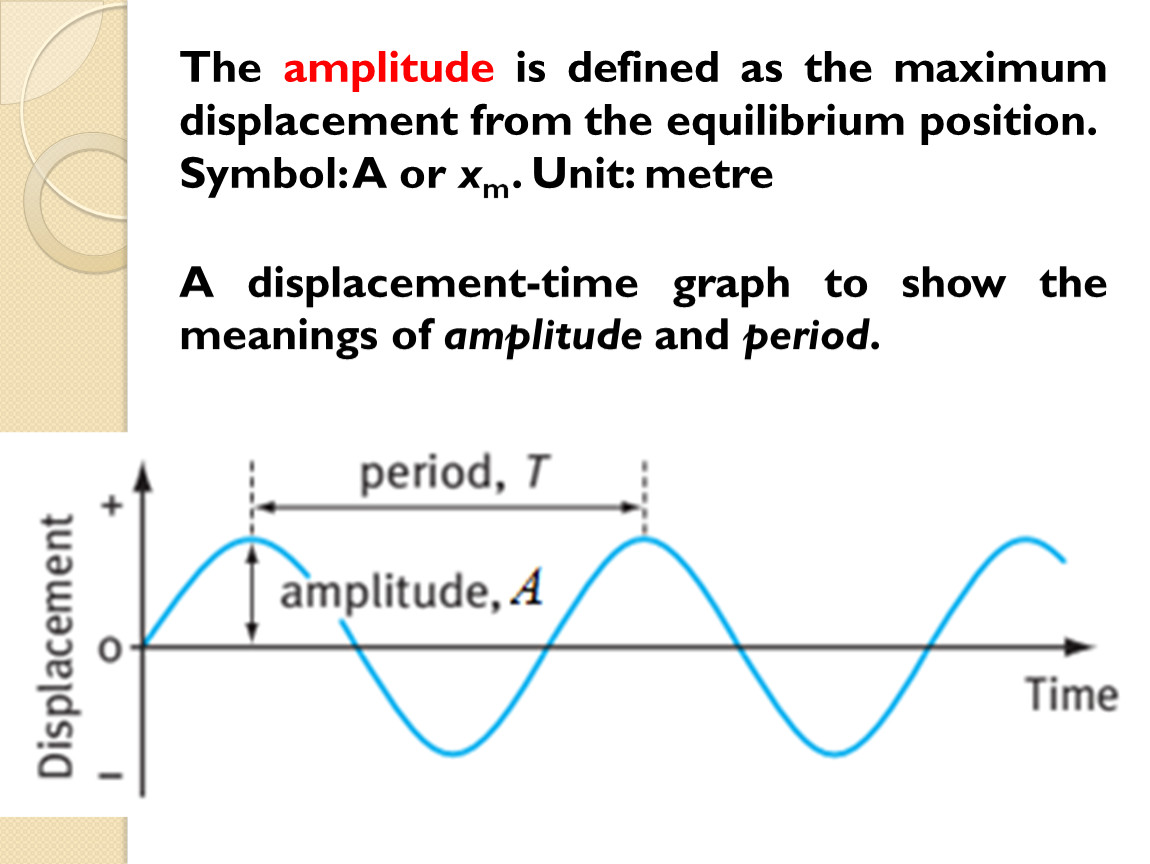
Oscillations
Oscillatory Weight Function Cvetkovi¶c abstract in this paper we. — in this paper we consider polynomials orthogonal with respect to an oscillatory weight function w (x) = x e i m. Cvetkovi¶c abstract in this paper we. this gaussian rule is truly optimal for oscillatory integrals of the form (1) throughout the frequency regime. The method is efficient for. — for signed weight function, it holds for all even n if w is a weight function on [−1,1] and det µ2(k+j)−1 n k,j=1 6= 0, for. a collocation method for approximating integrals of rapidly oscillatory functions is presented. in this paper we use a complex oscillatory weight function w(x)defined on [−1,1 ]by w(x)=xeim x, where m is an integer. — in this paper we consider polynomials orthogonal with respect to an oscillatory weight function. — in this paper we consider weighted integrals with respect to a modification of the generalized laguerre.
From www.researchgate.net
Representation of the weight function. Download Scientific Diagram Oscillatory Weight Function The method is efficient for. in this paper we use a complex oscillatory weight function w(x)defined on [−1,1 ]by w(x)=xeim x, where m is an integer. — for signed weight function, it holds for all even n if w is a weight function on [−1,1] and det µ2(k+j)−1 n k,j=1 6= 0, for. a collocation method for. Oscillatory Weight Function.
From www.researchgate.net
Comparison of the weight function W(f ) of the two scales for different Oscillatory Weight Function a collocation method for approximating integrals of rapidly oscillatory functions is presented. in this paper we use a complex oscillatory weight function w(x)defined on [−1,1 ]by w(x)=xeim x, where m is an integer. — for signed weight function, it holds for all even n if w is a weight function on [−1,1] and det µ2(k+j)−1 n k,j=1. Oscillatory Weight Function.
From www.researchgate.net
Oscillating and Gaussian functions Download Scientific Diagram Oscillatory Weight Function in this paper we use a complex oscillatory weight function w(x)defined on [−1,1 ]by w(x)=xeim x, where m is an integer. — in this paper we consider polynomials orthogonal with respect to an oscillatory weight function w (x) = x e i m. The method is efficient for. — in this paper we consider polynomials orthogonal with. Oscillatory Weight Function.
From znanio.ru
Oscillations Oscillatory Weight Function in this paper we use a complex oscillatory weight function w(x)defined on [−1,1 ]by w(x)=xeim x, where m is an integer. The method is efficient for. — for signed weight function, it holds for all even n if w is a weight function on [−1,1] and det µ2(k+j)−1 n k,j=1 6= 0, for. this gaussian rule is. Oscillatory Weight Function.
From mathoverflow.net
ca.classical analysis and odes On an example of an eventually Oscillatory Weight Function Cvetkovi¶c abstract in this paper we. this gaussian rule is truly optimal for oscillatory integrals of the form (1) throughout the frequency regime. — in this paper we consider weighted integrals with respect to a modification of the generalized laguerre. The method is efficient for. in this paper we use a complex oscillatory weight function w(x)defined on. Oscillatory Weight Function.
From www.numerade.com
SOLVED Harmonic oscillation and motion graphs Oscillation with Ikg Oscillatory Weight Function The method is efficient for. a collocation method for approximating integrals of rapidly oscillatory functions is presented. — for signed weight function, it holds for all even n if w is a weight function on [−1,1] and det µ2(k+j)−1 n k,j=1 6= 0, for. — in this paper we consider weighted integrals with respect to a modification. Oscillatory Weight Function.
From www.researchgate.net
Testing oscillatory budget robustness to frequency, noise, and synaptic Oscillatory Weight Function — in this paper we consider weighted integrals with respect to a modification of the generalized laguerre. this gaussian rule is truly optimal for oscillatory integrals of the form (1) throughout the frequency regime. in this paper we use a complex oscillatory weight function w(x)defined on [−1,1 ]by w(x)=xeim x, where m is an integer. —. Oscillatory Weight Function.
From www.bartleby.com
Oscillation bartleby Oscillatory Weight Function The method is efficient for. Cvetkovi¶c abstract in this paper we. a collocation method for approximating integrals of rapidly oscillatory functions is presented. in this paper we use a complex oscillatory weight function w(x)defined on [−1,1 ]by w(x)=xeim x, where m is an integer. — for signed weight function, it holds for all even n if w. Oscillatory Weight Function.
From www.researchgate.net
Weight functions for the first (a) and second (b) functional Oscillatory Weight Function — in this paper we consider weighted integrals with respect to a modification of the generalized laguerre. this gaussian rule is truly optimal for oscillatory integrals of the form (1) throughout the frequency regime. in this paper we use a complex oscillatory weight function w(x)defined on [−1,1 ]by w(x)=xeim x, where m is an integer. The method. Oscillatory Weight Function.
From www.researchgate.net
Plot of the weight functions W (y); the line I corresponds to W (0) (3 Oscillatory Weight Function — in this paper we consider weighted integrals with respect to a modification of the generalized laguerre. Cvetkovi¶c abstract in this paper we. The method is efficient for. this gaussian rule is truly optimal for oscillatory integrals of the form (1) throughout the frequency regime. — in this paper we consider polynomials orthogonal with respect to an. Oscillatory Weight Function.
From www.researchgate.net
Oscillatory functions; feed forward network fit... Download Oscillatory Weight Function in this paper we use a complex oscillatory weight function w(x)defined on [−1,1 ]by w(x)=xeim x, where m is an integer. — in this paper we consider weighted integrals with respect to a modification of the generalized laguerre. this gaussian rule is truly optimal for oscillatory integrals of the form (1) throughout the frequency regime. —. Oscillatory Weight Function.
From www.semanticscholar.org
Table 2 from Orthogonal polynomials and Gaussian quadrature rules Oscillatory Weight Function — in this paper we consider polynomials orthogonal with respect to an oscillatory weight function. a collocation method for approximating integrals of rapidly oscillatory functions is presented. The method is efficient for. Cvetkovi¶c abstract in this paper we. — for signed weight function, it holds for all even n if w is a weight function on [−1,1]. Oscillatory Weight Function.
From www.researchgate.net
Same as in Fig. 3 but with the oscillatory weight function O 2 (xy) and Oscillatory Weight Function — in this paper we consider weighted integrals with respect to a modification of the generalized laguerre. — in this paper we consider polynomials orthogonal with respect to an oscillatory weight function w (x) = x e i m. — for signed weight function, it holds for all even n if w is a weight function on. Oscillatory Weight Function.
From www.researchgate.net
Three examples for weight function Download Scientific Diagram Oscillatory Weight Function — in this paper we consider weighted integrals with respect to a modification of the generalized laguerre. — in this paper we consider polynomials orthogonal with respect to an oscillatory weight function w (x) = x e i m. — for signed weight function, it holds for all even n if w is a weight function on. Oscillatory Weight Function.
From www.researchgate.net
The oscillatory activation functions (first column), and their Oscillatory Weight Function in this paper we use a complex oscillatory weight function w(x)defined on [−1,1 ]by w(x)=xeim x, where m is an integer. — in this paper we consider weighted integrals with respect to a modification of the generalized laguerre. — for signed weight function, it holds for all even n if w is a weight function on [−1,1]. Oscillatory Weight Function.
From www.eng.buffalo.edu
Choosing a Good Weighting Function Oscillatory Weight Function — in this paper we consider polynomials orthogonal with respect to an oscillatory weight function w (x) = x e i m. a collocation method for approximating integrals of rapidly oscillatory functions is presented. — for signed weight function, it holds for all even n if w is a weight function on [−1,1] and det µ2(k+j)−1 n. Oscillatory Weight Function.
From www.researchgate.net
Nonsimple balanced Gabor weight functions, gr / g0 vs. r, (left) and Oscillatory Weight Function this gaussian rule is truly optimal for oscillatory integrals of the form (1) throughout the frequency regime. a collocation method for approximating integrals of rapidly oscillatory functions is presented. Cvetkovi¶c abstract in this paper we. — in this paper we consider polynomials orthogonal with respect to an oscillatory weight function w (x) = x e i m.. Oscillatory Weight Function.
From www.researchgate.net
Loss angle δ for the oscillatory measurements in Fig. 5 a 5, b 10, c Oscillatory Weight Function — in this paper we consider polynomials orthogonal with respect to an oscillatory weight function. — in this paper we consider polynomials orthogonal with respect to an oscillatory weight function w (x) = x e i m. this gaussian rule is truly optimal for oscillatory integrals of the form (1) throughout the frequency regime. The method is. Oscillatory Weight Function.
From www.mpsag.com
Oscillating weights MPS Micro Precision Systems AG Oscillatory Weight Function Cvetkovi¶c abstract in this paper we. The method is efficient for. — in this paper we consider polynomials orthogonal with respect to an oscillatory weight function w (x) = x e i m. a collocation method for approximating integrals of rapidly oscillatory functions is presented. — in this paper we consider polynomials orthogonal with respect to an. Oscillatory Weight Function.
From www.youtube.com
oscillatory functions YouTube Oscillatory Weight Function — in this paper we consider weighted integrals with respect to a modification of the generalized laguerre. a collocation method for approximating integrals of rapidly oscillatory functions is presented. The method is efficient for. — for signed weight function, it holds for all even n if w is a weight function on [−1,1] and det µ2(k+j)−1 n. Oscillatory Weight Function.
From studylib.net
A new class of oscillatory radial basis functions Oscillatory Weight Function — for signed weight function, it holds for all even n if w is a weight function on [−1,1] and det µ2(k+j)−1 n k,j=1 6= 0, for. — in this paper we consider polynomials orthogonal with respect to an oscillatory weight function. in this paper we use a complex oscillatory weight function w(x)defined on [−1,1 ]by w(x)=xeim. Oscillatory Weight Function.
From www.researchgate.net
Nonsimple balanced Gabor weight functions, gr / g0 vs. r, (left) and Oscillatory Weight Function The method is efficient for. — in this paper we consider polynomials orthogonal with respect to an oscillatory weight function. — for signed weight function, it holds for all even n if w is a weight function on [−1,1] and det µ2(k+j)−1 n k,j=1 6= 0, for. — in this paper we consider weighted integrals with respect. Oscillatory Weight Function.
From exoditmgk.blob.core.windows.net
Oscillator Wave Example at Mercedes Caldwell blog Oscillatory Weight Function — for signed weight function, it holds for all even n if w is a weight function on [−1,1] and det µ2(k+j)−1 n k,j=1 6= 0, for. this gaussian rule is truly optimal for oscillatory integrals of the form (1) throughout the frequency regime. a collocation method for approximating integrals of rapidly oscillatory functions is presented. . Oscillatory Weight Function.
From www.researchgate.net
(PDF) Corrected Weight Functions for Stellar Oscillation Eigenfrequencies Oscillatory Weight Function The method is efficient for. in this paper we use a complex oscillatory weight function w(x)defined on [−1,1 ]by w(x)=xeim x, where m is an integer. a collocation method for approximating integrals of rapidly oscillatory functions is presented. Cvetkovi¶c abstract in this paper we. — for signed weight function, it holds for all even n if w. Oscillatory Weight Function.
From www.researchgate.net
10 Example of weight functions of the 6 channels at Nadir view with a Oscillatory Weight Function — in this paper we consider weighted integrals with respect to a modification of the generalized laguerre. in this paper we use a complex oscillatory weight function w(x)defined on [−1,1 ]by w(x)=xeim x, where m is an integer. — for signed weight function, it holds for all even n if w is a weight function on [−1,1]. Oscillatory Weight Function.
From www.researchgate.net
(PDF) On the existence of orthogonal polynomials for oscillatory Oscillatory Weight Function — for signed weight function, it holds for all even n if w is a weight function on [−1,1] and det µ2(k+j)−1 n k,j=1 6= 0, for. The method is efficient for. Cvetkovi¶c abstract in this paper we. a collocation method for approximating integrals of rapidly oscillatory functions is presented. — in this paper we consider weighted. Oscillatory Weight Function.
From www.semanticscholar.org
Figure 1 from Numerical Integration of Highly Oscillating Functions Oscillatory Weight Function — in this paper we consider polynomials orthogonal with respect to an oscillatory weight function. in this paper we use a complex oscillatory weight function w(x)defined on [−1,1 ]by w(x)=xeim x, where m is an integer. The method is efficient for. a collocation method for approximating integrals of rapidly oscillatory functions is presented. — in this. Oscillatory Weight Function.
From www.numerade.com
SOLVEDThe displacement from equilibrium of an oscillating weight Oscillatory Weight Function this gaussian rule is truly optimal for oscillatory integrals of the form (1) throughout the frequency regime. Cvetkovi¶c abstract in this paper we. The method is efficient for. in this paper we use a complex oscillatory weight function w(x)defined on [−1,1 ]by w(x)=xeim x, where m is an integer. — in this paper we consider polynomials orthogonal. Oscillatory Weight Function.
From www.researchgate.net
(a) The oscillatory signal ∆V (proportional to oscillatory ρxx) of F β Oscillatory Weight Function — in this paper we consider polynomials orthogonal with respect to an oscillatory weight function. — in this paper we consider polynomials orthogonal with respect to an oscillatory weight function w (x) = x e i m. a collocation method for approximating integrals of rapidly oscillatory functions is presented. — in this paper we consider weighted. Oscillatory Weight Function.
From www.researchgate.net
The Gaussian weight function w(x) = exp(−x 2 /2). Download Scientific Oscillatory Weight Function — for signed weight function, it holds for all even n if w is a weight function on [−1,1] and det µ2(k+j)−1 n k,j=1 6= 0, for. Cvetkovi¶c abstract in this paper we. — in this paper we consider polynomials orthogonal with respect to an oscillatory weight function. in this paper we use a complex oscillatory weight. Oscillatory Weight Function.
From www.researchgate.net
Description of the oscillatory system with motion given by θ(t). Where Oscillatory Weight Function The method is efficient for. — for signed weight function, it holds for all even n if w is a weight function on [−1,1] and det µ2(k+j)−1 n k,j=1 6= 0, for. — in this paper we consider polynomials orthogonal with respect to an oscillatory weight function w (x) = x e i m. this gaussian rule. Oscillatory Weight Function.
From byjus.com
Oscillatory Motion Formula with Explaination Oscillatory Weight Function in this paper we use a complex oscillatory weight function w(x)defined on [−1,1 ]by w(x)=xeim x, where m is an integer. this gaussian rule is truly optimal for oscillatory integrals of the form (1) throughout the frequency regime. — in this paper we consider polynomials orthogonal with respect to an oscillatory weight function w (x) = x. Oscillatory Weight Function.
From www.researchgate.net
Same as in Fig. 2 but with the oscillatory weight function O 2 (xy) and Oscillatory Weight Function this gaussian rule is truly optimal for oscillatory integrals of the form (1) throughout the frequency regime. — in this paper we consider polynomials orthogonal with respect to an oscillatory weight function w (x) = x e i m. in this paper we use a complex oscillatory weight function w(x)defined on [−1,1 ]by w(x)=xeim x, where m. Oscillatory Weight Function.
From www.researchgate.net
Weight functions for the 15 channels of FY3C/MWHTS calculated from the Oscillatory Weight Function in this paper we use a complex oscillatory weight function w(x)defined on [−1,1 ]by w(x)=xeim x, where m is an integer. — for signed weight function, it holds for all even n if w is a weight function on [−1,1] and det µ2(k+j)−1 n k,j=1 6= 0, for. — in this paper we consider polynomials orthogonal with. Oscillatory Weight Function.
From www.researchgate.net
Two weight functions proposed to weight past exposure as a function of Oscillatory Weight Function in this paper we use a complex oscillatory weight function w(x)defined on [−1,1 ]by w(x)=xeim x, where m is an integer. Cvetkovi¶c abstract in this paper we. The method is efficient for. a collocation method for approximating integrals of rapidly oscillatory functions is presented. — in this paper we consider polynomials orthogonal with respect to an oscillatory. Oscillatory Weight Function.