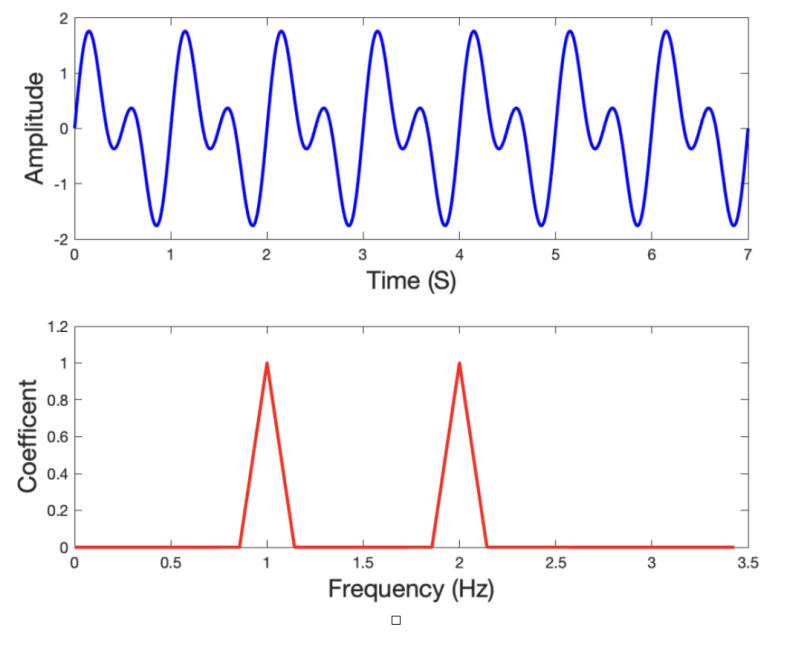
Signal Processing Fourier Series at Sara Gosman blog

Signal Processing Fourier Series. Once one has obtained a solid understanding of the fundamentals of fourier series analysis and the general derivation of the fourier coefficients, it is useful to. The first deals with periodic functions, and the second deals with. Representing a signal by its frequency. Fourier series represent signals by their frequency content. Besides theoretical mathematical applications, fourier series have many modern applications, including areas such as signal processing,. A fourier series is a continuous, periodic function created by a summation of harmonically related sinusoidal functions. It has several different, but equivalent, forms, shown here. The fourier series is a specialized tool that allows for any periodic signal (subject to certain conditions) to be decomposed into an. The pillars of fourier analysis are fourier series and fourier transforms.

Besides theoretical mathematical applications, fourier series have many modern applications, including areas such as signal processing,. It has several different, but equivalent, forms, shown here. The pillars of fourier analysis are fourier series and fourier transforms. Once one has obtained a solid understanding of the fundamentals of fourier series analysis and the general derivation of the fourier coefficients, it is useful to. A fourier series is a continuous, periodic function created by a summation of harmonically related sinusoidal functions. Representing a signal by its frequency. The fourier series is a specialized tool that allows for any periodic signal (subject to certain conditions) to be decomposed into an. Fourier series represent signals by their frequency content. The first deals with periodic functions, and the second deals with.

Fourier Transform Table Hertz Elcho Table

Signal Processing Fourier Series Fourier series represent signals by their frequency content. Besides theoretical mathematical applications, fourier series have many modern applications, including areas such as signal processing,. The pillars of fourier analysis are fourier series and fourier transforms. Fourier series represent signals by their frequency content. It has several different, but equivalent, forms, shown here. The first deals with periodic functions, and the second deals with. Once one has obtained a solid understanding of the fundamentals of fourier series analysis and the general derivation of the fourier coefficients, it is useful to. The fourier series is a specialized tool that allows for any periodic signal (subject to certain conditions) to be decomposed into an. A fourier series is a continuous, periodic function created by a summation of harmonically related sinusoidal functions. Representing a signal by its frequency.