Group Action Examples . The group sn has a natural action on [n] since each element of sn is a permutation. An action of the group \(g\) on the set \(x\) is a group. Recall the definition of an action: An action of g on s is a. Let g be a group and let s be a set. More generally sym( ) acts on. In each of the following examples we will give a group g operating on a set s. Let \(g\) be a group and let \(x\) be a set. The standard example of a group action is when \ (g\) equals the symmetric group \ (s_n\) \ ( (\)or a subgroup of \ (s_n)\) and \ (x = \. A group action is a way of assigning elements of a group to symmetries of an object in a way that respects the group operation.
from learn.microsoft.com
In each of the following examples we will give a group g operating on a set s. Let g be a group and let s be a set. The group sn has a natural action on [n] since each element of sn is a permutation. An action of g on s is a. An action of the group \(g\) on the set \(x\) is a group. Recall the definition of an action: The standard example of a group action is when \ (g\) equals the symmetric group \ (s_n\) \ ( (\)or a subgroup of \ (s_n)\) and \ (x = \. More generally sym( ) acts on. Let \(g\) be a group and let \(x\) be a set. A group action is a way of assigning elements of a group to symmetries of an object in a way that respects the group operation.
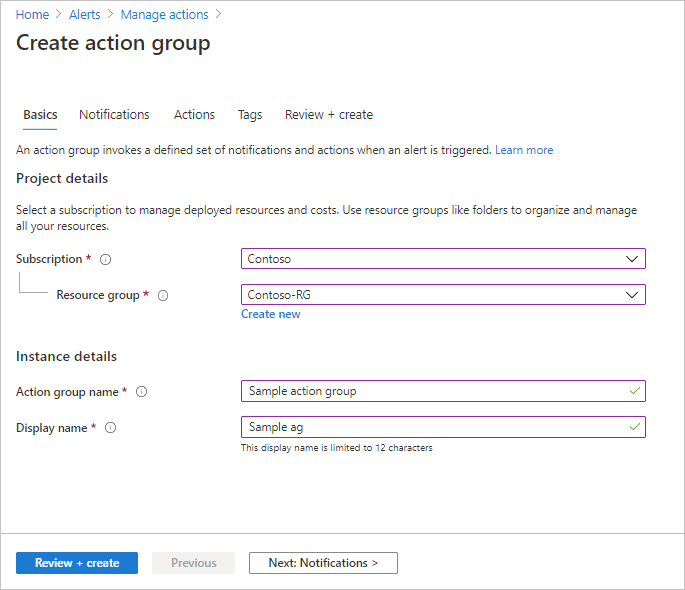
Azure Monitor action groups Azure Monitor Microsoft Learn
Group Action Examples A group action is a way of assigning elements of a group to symmetries of an object in a way that respects the group operation. The group sn has a natural action on [n] since each element of sn is a permutation. An action of the group \(g\) on the set \(x\) is a group. A group action is a way of assigning elements of a group to symmetries of an object in a way that respects the group operation. Recall the definition of an action: In each of the following examples we will give a group g operating on a set s. Let \(g\) be a group and let \(x\) be a set. More generally sym( ) acts on. Let g be a group and let s be a set. An action of g on s is a. The standard example of a group action is when \ (g\) equals the symmetric group \ (s_n\) \ ( (\)or a subgroup of \ (s_n)\) and \ (x = \.
From helpfulprofessor.com
13 Affirmative Action Examples (2024) Group Action Examples An action of the group \(g\) on the set \(x\) is a group. The group sn has a natural action on [n] since each element of sn is a permutation. More generally sym( ) acts on. A group action is a way of assigning elements of a group to symmetries of an object in a way that respects the group. Group Action Examples.
From learn.microsoft.com
Azure Monitor action groups Azure Monitor Microsoft Learn Group Action Examples More generally sym( ) acts on. Recall the definition of an action: A group action is a way of assigning elements of a group to symmetries of an object in a way that respects the group operation. An action of g on s is a. Let g be a group and let s be a set. Let \(g\) be a. Group Action Examples.
From pdfprof.com
les verbes d'action pdf Group Action Examples More generally sym( ) acts on. An action of the group \(g\) on the set \(x\) is a group. Recall the definition of an action: The group sn has a natural action on [n] since each element of sn is a permutation. In each of the following examples we will give a group g operating on a set s. A. Group Action Examples.
From printable.conaresvirtual.edu.sv
Free Printable Action Plan Template Group Action Examples In each of the following examples we will give a group g operating on a set s. Let g be a group and let s be a set. Let \(g\) be a group and let \(x\) be a set. The group sn has a natural action on [n] since each element of sn is a permutation. Recall the definition of. Group Action Examples.
From www.allbusinesstemplates.com
Gratis Individueel studentenactieplan Group Action Examples A group action is a way of assigning elements of a group to symmetries of an object in a way that respects the group operation. The group sn has a natural action on [n] since each element of sn is a permutation. An action of g on s is a. Recall the definition of an action: Let g be a. Group Action Examples.
From climateactions.ca
Action for Community Groups Climate Actions Group Action Examples In each of the following examples we will give a group g operating on a set s. An action of g on s is a. Recall the definition of an action: Let g be a group and let s be a set. The group sn has a natural action on [n] since each element of sn is a permutation. A. Group Action Examples.
From learn.microsoft.com
Azure Monitor action groups Azure Monitor Microsoft Learn Group Action Examples More generally sym( ) acts on. An action of g on s is a. Let g be a group and let s be a set. In each of the following examples we will give a group g operating on a set s. An action of the group \(g\) on the set \(x\) is a group. A group action is a. Group Action Examples.
From aboutenglishlanguage.com
Action verbs; Easy Examples & 250+ List Learn English online free Group Action Examples In each of the following examples we will give a group g operating on a set s. The standard example of a group action is when \ (g\) equals the symmetric group \ (s_n\) \ ( (\)or a subgroup of \ (s_n)\) and \ (x = \. Recall the definition of an action: A group action is a way of. Group Action Examples.
From edit.org
Free Action Plan Templates Group Action Examples More generally sym( ) acts on. Recall the definition of an action: A group action is a way of assigning elements of a group to symmetries of an object in a way that respects the group operation. In each of the following examples we will give a group g operating on a set s. Let g be a group and. Group Action Examples.
From www.youtube.com
Group Action On a Set Part1 YouTube Group Action Examples More generally sym( ) acts on. The standard example of a group action is when \ (g\) equals the symmetric group \ (s_n\) \ ( (\)or a subgroup of \ (s_n)\) and \ (x = \. In each of the following examples we will give a group g operating on a set s. Recall the definition of an action: A. Group Action Examples.
From www.youtube.com
Examples of Group Actions YouTube Group Action Examples Recall the definition of an action: An action of g on s is a. Let \(g\) be a group and let \(x\) be a set. The group sn has a natural action on [n] since each element of sn is a permutation. In each of the following examples we will give a group g operating on a set s. A. Group Action Examples.
From www.studocu.com
Group Actions (Day 12 Notes) Group Actions (Section 16) 1 Group Action Examples An action of g on s is a. In each of the following examples we will give a group g operating on a set s. More generally sym( ) acts on. Let \(g\) be a group and let \(x\) be a set. The group sn has a natural action on [n] since each element of sn is a permutation. The. Group Action Examples.
From www.managementguru.net
Top Five Reasons Why Strategic Plans Fail Management Guru Group Action Examples Let \(g\) be a group and let \(x\) be a set. Let g be a group and let s be a set. Recall the definition of an action: An action of the group \(g\) on the set \(x\) is a group. A group action is a way of assigning elements of a group to symmetries of an object in a. Group Action Examples.
From www.doctemplates.net
58 Free Action Plan Templates & Samples An Easy Way to Plan Actions Group Action Examples Let \(g\) be a group and let \(x\) be a set. More generally sym( ) acts on. In each of the following examples we will give a group g operating on a set s. Let g be a group and let s be a set. Recall the definition of an action: An action of g on s is a. The. Group Action Examples.
From buddy.works
Introducing New group features and action selection on run Group Action Examples An action of the group \(g\) on the set \(x\) is a group. An action of g on s is a. Recall the definition of an action: Let g be a group and let s be a set. The standard example of a group action is when \ (g\) equals the symmetric group \ (s_n\) \ ( (\)or a subgroup. Group Action Examples.
From www.studocu.com
Group actions on sets are A group action on a set is a way of Group Action Examples In each of the following examples we will give a group g operating on a set s. More generally sym( ) acts on. An action of the group \(g\) on the set \(x\) is a group. Let \(g\) be a group and let \(x\) be a set. The standard example of a group action is when \ (g\) equals the. Group Action Examples.
From www.opirgyork.org
Action Groups OPIRG York Group Action Examples The standard example of a group action is when \ (g\) equals the symmetric group \ (s_n\) \ ( (\)or a subgroup of \ (s_n)\) and \ (x = \. A group action is a way of assigning elements of a group to symmetries of an object in a way that respects the group operation. Let g be a group. Group Action Examples.
From helpfulprofessor.com
Deviance in Sociology 25 Examples & Definition (2024) Group Action Examples The group sn has a natural action on [n] since each element of sn is a permutation. Recall the definition of an action: An action of the group \(g\) on the set \(x\) is a group. More generally sym( ) acts on. Let g be a group and let s be a set. A group action is a way of. Group Action Examples.
From med.umn.edu
CWIMS Action Groups Medical School Group Action Examples An action of the group \(g\) on the set \(x\) is a group. Let g be a group and let s be a set. A group action is a way of assigning elements of a group to symmetries of an object in a way that respects the group operation. In each of the following examples we will give a group. Group Action Examples.
From pngtree.com
Actions Clipart Cartoon Kids In Different Groups Vector, Actions Group Action Examples Let \(g\) be a group and let \(x\) be a set. Recall the definition of an action: An action of the group \(g\) on the set \(x\) is a group. More generally sym( ) acts on. An action of g on s is a. Let g be a group and let s be a set. A group action is a. Group Action Examples.
From helpfulprofessor.com
50 Social Groups Examples (2024) Group Action Examples A group action is a way of assigning elements of a group to symmetries of an object in a way that respects the group operation. Let \(g\) be a group and let \(x\) be a set. The group sn has a natural action on [n] since each element of sn is a permutation. In each of the following examples we. Group Action Examples.
From www.youtube.com
Group action meaning of Group action YouTube Group Action Examples The standard example of a group action is when \ (g\) equals the symmetric group \ (s_n\) \ ( (\)or a subgroup of \ (s_n)\) and \ (x = \. An action of g on s is a. Let g be a group and let s be a set. The group sn has a natural action on [n] since each. Group Action Examples.
From doc.oroinc.com
Action Groups OroCRM and OroPlatform Documentation Group Action Examples Recall the definition of an action: Let g be a group and let s be a set. An action of g on s is a. Let \(g\) be a group and let \(x\) be a set. In each of the following examples we will give a group g operating on a set s. An action of the group \(g\) on. Group Action Examples.
From learn.microsoft.com
IT Service Management Connector in Log Analytics Azure Monitor Group Action Examples A group action is a way of assigning elements of a group to symmetries of an object in a way that respects the group operation. In each of the following examples we will give a group g operating on a set s. Recall the definition of an action: An action of the group \(g\) on the set \(x\) is a. Group Action Examples.
From earth911.com
Raising Kids Who Take Action Value of Teamwork Skills Earth911 Group Action Examples In each of the following examples we will give a group g operating on a set s. An action of the group \(g\) on the set \(x\) is a group. An action of g on s is a. The group sn has a natural action on [n] since each element of sn is a permutation. Let g be a group. Group Action Examples.
From www.pinterest.com
200+ Common Action Verbs in English • 7ESL Learn english, English Group Action Examples Let g be a group and let s be a set. Recall the definition of an action: An action of g on s is a. A group action is a way of assigning elements of a group to symmetries of an object in a way that respects the group operation. An action of the group \(g\) on the set \(x\). Group Action Examples.
From www.pinterest.co.uk
English Vocabulary; Action Verbs List of Common Action Verbs Group Action Examples Recall the definition of an action: More generally sym( ) acts on. A group action is a way of assigning elements of a group to symmetries of an object in a way that respects the group operation. Let \(g\) be a group and let \(x\) be a set. The group sn has a natural action on [n] since each element. Group Action Examples.
From www.examples.com
Work Action Plan 9+ Examples, Format, Pdf Examples Group Action Examples An action of g on s is a. Let g be a group and let s be a set. An action of the group \(g\) on the set \(x\) is a group. Recall the definition of an action: A group action is a way of assigning elements of a group to symmetries of an object in a way that respects. Group Action Examples.
From buddy.works
Introducing New group features and action selection on run Group Action Examples The group sn has a natural action on [n] since each element of sn is a permutation. Let \(g\) be a group and let \(x\) be a set. In each of the following examples we will give a group g operating on a set s. More generally sym( ) acts on. Recall the definition of an action: A group action. Group Action Examples.
From www.examples.com
Work Action Plan 9+ Examples, Format, Pdf Examples Group Action Examples The group sn has a natural action on [n] since each element of sn is a permutation. Recall the definition of an action: An action of the group \(g\) on the set \(x\) is a group. Let \(g\) be a group and let \(x\) be a set. An action of g on s is a. In each of the following. Group Action Examples.
From helpfulprofessor.com
Social Action Theory Examples and Definition (2024) Group Action Examples Let \(g\) be a group and let \(x\) be a set. In each of the following examples we will give a group g operating on a set s. The group sn has a natural action on [n] since each element of sn is a permutation. A group action is a way of assigning elements of a group to symmetries of. Group Action Examples.
From worksheetoffesylultuffrg.z21.web.core.windows.net
Visual Motor Skill Activities For Kids Group Action Examples Recall the definition of an action: The group sn has a natural action on [n] since each element of sn is a permutation. Let \(g\) be a group and let \(x\) be a set. An action of the group \(g\) on the set \(x\) is a group. A group action is a way of assigning elements of a group to. Group Action Examples.
From templates.udlvirtual.edu.pe
Business Action Plan Template Free Download Printable Templates Group Action Examples The standard example of a group action is when \ (g\) equals the symmetric group \ (s_n\) \ ( (\)or a subgroup of \ (s_n)\) and \ (x = \. An action of the group \(g\) on the set \(x\) is a group. A group action is a way of assigning elements of a group to symmetries of an object. Group Action Examples.
From www.freepik.com
Premium Vector Group action abstract concept vector illustrations Group Action Examples Let \(g\) be a group and let \(x\) be a set. An action of g on s is a. In each of the following examples we will give a group g operating on a set s. The standard example of a group action is when \ (g\) equals the symmetric group \ (s_n\) \ ( (\)or a subgroup of \. Group Action Examples.
From www.prehabexercises.com
Synergistic Training Improve Mobility, Stability and Strength Group Action Examples The group sn has a natural action on [n] since each element of sn is a permutation. A group action is a way of assigning elements of a group to symmetries of an object in a way that respects the group operation. In each of the following examples we will give a group g operating on a set s. Recall. Group Action Examples.