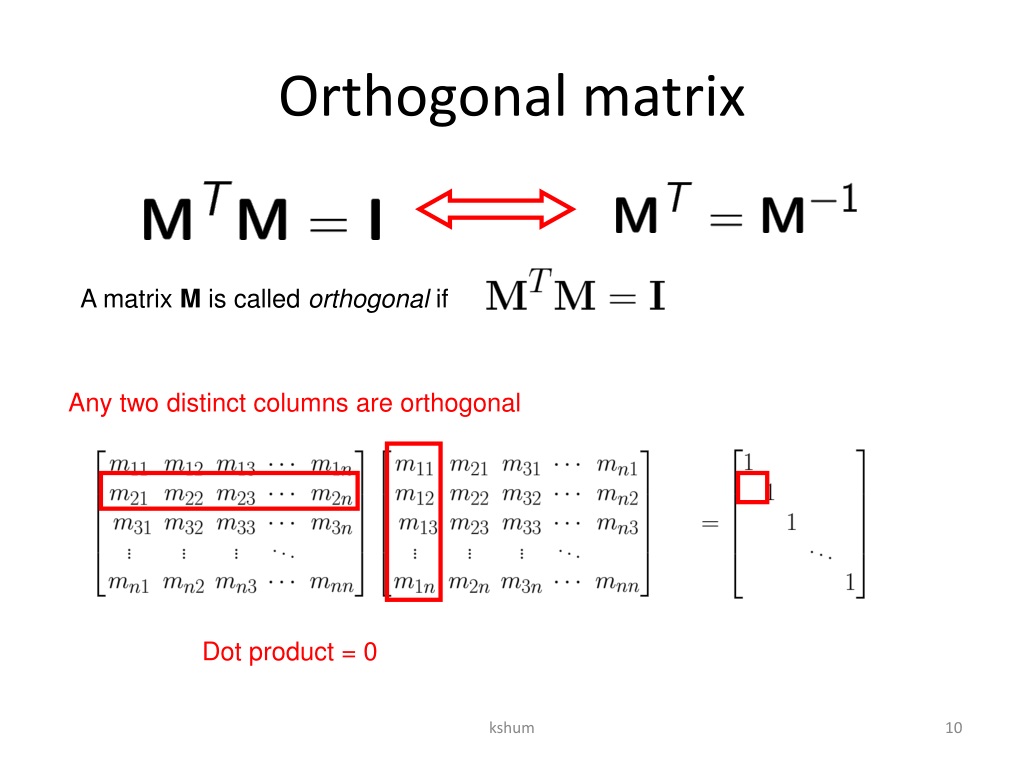
Orthogonal Matrix Defi . Or we can say when the product of a square matrix and its transpose gives an identity matrix, then the square matrix is known as an. An orthogonal matrix is a square matrix a if and only its transpose is as same as its inverse. An orthogonal matrix \(u\), from definition 4.11.7, is one in which \(uu^{t} = i\). In other words, the transpose of an orthogonal. In particular, taking v = w means that lengths are preserved by orthogonal. From this definition, we can. A matrix is called orthogonal matrix when the transpose of matrix is inverse of that matrix or the product of matrix and it’s transpose is. A matrix a ∈ gl. An orthogonal matrix is a square matrix whose rows and columns are orthogonal unit vectors (i.e., orthonormal vectors), meaning that their dot. N (r) is orthogonal if av · aw = v · w for all vectors v and w.
from www.slideserve.com
Or we can say when the product of a square matrix and its transpose gives an identity matrix, then the square matrix is known as an. An orthogonal matrix \(u\), from definition 4.11.7, is one in which \(uu^{t} = i\). In particular, taking v = w means that lengths are preserved by orthogonal. An orthogonal matrix is a square matrix whose rows and columns are orthogonal unit vectors (i.e., orthonormal vectors), meaning that their dot. In other words, the transpose of an orthogonal. A matrix is called orthogonal matrix when the transpose of matrix is inverse of that matrix or the product of matrix and it’s transpose is. From this definition, we can. An orthogonal matrix is a square matrix a if and only its transpose is as same as its inverse. A matrix a ∈ gl. N (r) is orthogonal if av · aw = v · w for all vectors v and w.
PPT ENGG2013 Unit 19 The principal axes theorem PowerPoint
Orthogonal Matrix Defi In other words, the transpose of an orthogonal. An orthogonal matrix is a square matrix whose rows and columns are orthogonal unit vectors (i.e., orthonormal vectors), meaning that their dot. In particular, taking v = w means that lengths are preserved by orthogonal. A matrix is called orthogonal matrix when the transpose of matrix is inverse of that matrix or the product of matrix and it’s transpose is. Or we can say when the product of a square matrix and its transpose gives an identity matrix, then the square matrix is known as an. An orthogonal matrix is a square matrix a if and only its transpose is as same as its inverse. In other words, the transpose of an orthogonal. An orthogonal matrix \(u\), from definition 4.11.7, is one in which \(uu^{t} = i\). From this definition, we can. A matrix a ∈ gl. N (r) is orthogonal if av · aw = v · w for all vectors v and w.
From www.youtube.com
Properties of Orthogonal Matrix Example1 YouTube Orthogonal Matrix Defi An orthogonal matrix \(u\), from definition 4.11.7, is one in which \(uu^{t} = i\). A matrix a ∈ gl. An orthogonal matrix is a square matrix whose rows and columns are orthogonal unit vectors (i.e., orthonormal vectors), meaning that their dot. In particular, taking v = w means that lengths are preserved by orthogonal. An orthogonal matrix is a square. Orthogonal Matrix Defi.
From www.youtube.com
Orthogonal Matrix example YouTube Orthogonal Matrix Defi An orthogonal matrix is a square matrix a if and only its transpose is as same as its inverse. A matrix is called orthogonal matrix when the transpose of matrix is inverse of that matrix or the product of matrix and it’s transpose is. An orthogonal matrix is a square matrix whose rows and columns are orthogonal unit vectors (i.e.,. Orthogonal Matrix Defi.
From www.chegg.com
Solved Triangularisation with an orthogonal matrix Example Orthogonal Matrix Defi N (r) is orthogonal if av · aw = v · w for all vectors v and w. From this definition, we can. An orthogonal matrix \(u\), from definition 4.11.7, is one in which \(uu^{t} = i\). In particular, taking v = w means that lengths are preserved by orthogonal. An orthogonal matrix is a square matrix a if and. Orthogonal Matrix Defi.
From ar.inspiredpencil.com
Orthogonal Matrix Orthogonal Matrix Defi Or we can say when the product of a square matrix and its transpose gives an identity matrix, then the square matrix is known as an. From this definition, we can. In other words, the transpose of an orthogonal. An orthogonal matrix \(u\), from definition 4.11.7, is one in which \(uu^{t} = i\). An orthogonal matrix is a square matrix. Orthogonal Matrix Defi.
From www.toppr.com
An orthogonal matrix is Maths Questions Orthogonal Matrix Defi From this definition, we can. In particular, taking v = w means that lengths are preserved by orthogonal. In other words, the transpose of an orthogonal. N (r) is orthogonal if av · aw = v · w for all vectors v and w. An orthogonal matrix is a square matrix a if and only its transpose is as same. Orthogonal Matrix Defi.
From inputone.weebly.com
inputone Blog Orthogonal Matrix Defi In particular, taking v = w means that lengths are preserved by orthogonal. In other words, the transpose of an orthogonal. Or we can say when the product of a square matrix and its transpose gives an identity matrix, then the square matrix is known as an. N (r) is orthogonal if av · aw = v · w for. Orthogonal Matrix Defi.
From www.researchgate.net
Orthogonality Matrix Download Table Orthogonal Matrix Defi From this definition, we can. A matrix a ∈ gl. An orthogonal matrix is a square matrix a if and only its transpose is as same as its inverse. An orthogonal matrix \(u\), from definition 4.11.7, is one in which \(uu^{t} = i\). In particular, taking v = w means that lengths are preserved by orthogonal. In other words, the. Orthogonal Matrix Defi.
From slideplayer.com
Orthogonal Matrices & Symmetric Matrices ppt download Orthogonal Matrix Defi A matrix is called orthogonal matrix when the transpose of matrix is inverse of that matrix or the product of matrix and it’s transpose is. From this definition, we can. A matrix a ∈ gl. An orthogonal matrix is a square matrix whose rows and columns are orthogonal unit vectors (i.e., orthonormal vectors), meaning that their dot. In particular, taking. Orthogonal Matrix Defi.
From www.youtube.com
Linear Algebra Orthogonal Matrix YouTube Orthogonal Matrix Defi An orthogonal matrix is a square matrix a if and only its transpose is as same as its inverse. Or we can say when the product of a square matrix and its transpose gives an identity matrix, then the square matrix is known as an. An orthogonal matrix is a square matrix whose rows and columns are orthogonal unit vectors. Orthogonal Matrix Defi.
From www.youtube.com
What is Orthogonal Matrix and its Properties Kamaldheeriya YouTube Orthogonal Matrix Defi An orthogonal matrix is a square matrix whose rows and columns are orthogonal unit vectors (i.e., orthonormal vectors), meaning that their dot. A matrix is called orthogonal matrix when the transpose of matrix is inverse of that matrix or the product of matrix and it’s transpose is. N (r) is orthogonal if av · aw = v · w for. Orthogonal Matrix Defi.
From www.chegg.com
Solved a. Which of the matrices are orthogonal (has Orthogonal Matrix Defi A matrix a ∈ gl. Or we can say when the product of a square matrix and its transpose gives an identity matrix, then the square matrix is known as an. In particular, taking v = w means that lengths are preserved by orthogonal. A matrix is called orthogonal matrix when the transpose of matrix is inverse of that matrix. Orthogonal Matrix Defi.
From scoop.eduncle.com
Find orthogonal matrix and unitary matrix Orthogonal Matrix Defi An orthogonal matrix is a square matrix whose rows and columns are orthogonal unit vectors (i.e., orthonormal vectors), meaning that their dot. N (r) is orthogonal if av · aw = v · w for all vectors v and w. In particular, taking v = w means that lengths are preserved by orthogonal. In other words, the transpose of an. Orthogonal Matrix Defi.
From www.researchgate.net
Orthogonal coordinate system. The origin is at the centroid of the Orthogonal Matrix Defi A matrix is called orthogonal matrix when the transpose of matrix is inverse of that matrix or the product of matrix and it’s transpose is. An orthogonal matrix is a square matrix a if and only its transpose is as same as its inverse. In other words, the transpose of an orthogonal. An orthogonal matrix is a square matrix whose. Orthogonal Matrix Defi.
From 911weknow.com
[Linear Algebra] 9. Properties of orthogonal matrices 911 WeKnow Orthogonal Matrix Defi An orthogonal matrix is a square matrix a if and only its transpose is as same as its inverse. An orthogonal matrix \(u\), from definition 4.11.7, is one in which \(uu^{t} = i\). In particular, taking v = w means that lengths are preserved by orthogonal. Or we can say when the product of a square matrix and its transpose. Orthogonal Matrix Defi.
From limfadreams.weebly.com
Orthogonal matrix limfadreams Orthogonal Matrix Defi In other words, the transpose of an orthogonal. In particular, taking v = w means that lengths are preserved by orthogonal. An orthogonal matrix is a square matrix whose rows and columns are orthogonal unit vectors (i.e., orthonormal vectors), meaning that their dot. From this definition, we can. An orthogonal matrix \(u\), from definition 4.11.7, is one in which \(uu^{t}. Orthogonal Matrix Defi.
From www.youtube.com
Orthogonal Matrix What is orthogonal Matrix How to prove Orthogonal Orthogonal Matrix Defi N (r) is orthogonal if av · aw = v · w for all vectors v and w. Or we can say when the product of a square matrix and its transpose gives an identity matrix, then the square matrix is known as an. An orthogonal matrix \(u\), from definition 4.11.7, is one in which \(uu^{t} = i\). An orthogonal. Orthogonal Matrix Defi.
From www.youtube.com
Orthogonal Matrix Matrices and Determinants Class 12 IIT JEE Maths Orthogonal Matrix Defi From this definition, we can. In particular, taking v = w means that lengths are preserved by orthogonal. Or we can say when the product of a square matrix and its transpose gives an identity matrix, then the square matrix is known as an. A matrix a ∈ gl. N (r) is orthogonal if av · aw = v ·. Orthogonal Matrix Defi.
From inputone.weebly.com
inputone Blog Orthogonal Matrix Defi An orthogonal matrix is a square matrix a if and only its transpose is as same as its inverse. From this definition, we can. In particular, taking v = w means that lengths are preserved by orthogonal. A matrix is called orthogonal matrix when the transpose of matrix is inverse of that matrix or the product of matrix and it’s. Orthogonal Matrix Defi.
From teamlab.github.io
Basic Linear Algebra Orthogonal Matrix Defi An orthogonal matrix is a square matrix a if and only its transpose is as same as its inverse. Or we can say when the product of a square matrix and its transpose gives an identity matrix, then the square matrix is known as an. In particular, taking v = w means that lengths are preserved by orthogonal. In other. Orthogonal Matrix Defi.
From www.youtube.com
Orthogonal Matrix Definition Example Properties Class 12 Maths YouTube Orthogonal Matrix Defi Or we can say when the product of a square matrix and its transpose gives an identity matrix, then the square matrix is known as an. From this definition, we can. An orthogonal matrix is a square matrix a if and only its transpose is as same as its inverse. In other words, the transpose of an orthogonal. N (r). Orthogonal Matrix Defi.
From www.chegg.com
Solved Orthogonally diagonalize the matrix, giving an Orthogonal Matrix Defi An orthogonal matrix is a square matrix a if and only its transpose is as same as its inverse. Or we can say when the product of a square matrix and its transpose gives an identity matrix, then the square matrix is known as an. In particular, taking v = w means that lengths are preserved by orthogonal. A matrix. Orthogonal Matrix Defi.
From www.numerade.com
SOLVED Orthogonal Transformations Orthogonal Matrices In Exercises 12 Orthogonal Matrix Defi An orthogonal matrix \(u\), from definition 4.11.7, is one in which \(uu^{t} = i\). An orthogonal matrix is a square matrix a if and only its transpose is as same as its inverse. In other words, the transpose of an orthogonal. A matrix is called orthogonal matrix when the transpose of matrix is inverse of that matrix or the product. Orthogonal Matrix Defi.
From www.youtube.com
How to prove ORTHOGONAL Matrices YouTube Orthogonal Matrix Defi An orthogonal matrix is a square matrix whose rows and columns are orthogonal unit vectors (i.e., orthonormal vectors), meaning that their dot. In particular, taking v = w means that lengths are preserved by orthogonal. From this definition, we can. An orthogonal matrix \(u\), from definition 4.11.7, is one in which \(uu^{t} = i\). A matrix a ∈ gl. In. Orthogonal Matrix Defi.
From www.machinelearningplus.com
Linear Algebra Archives Machine Learning Plus Orthogonal Matrix Defi In other words, the transpose of an orthogonal. An orthogonal matrix \(u\), from definition 4.11.7, is one in which \(uu^{t} = i\). From this definition, we can. Or we can say when the product of a square matrix and its transpose gives an identity matrix, then the square matrix is known as an. An orthogonal matrix is a square matrix. Orthogonal Matrix Defi.
From www.slideserve.com
PPT ENGG2013 Unit 19 The principal axes theorem PowerPoint Orthogonal Matrix Defi From this definition, we can. A matrix a ∈ gl. In particular, taking v = w means that lengths are preserved by orthogonal. In other words, the transpose of an orthogonal. An orthogonal matrix is a square matrix whose rows and columns are orthogonal unit vectors (i.e., orthonormal vectors), meaning that their dot. An orthogonal matrix \(u\), from definition 4.11.7,. Orthogonal Matrix Defi.
From datascienceparichay.com
Numpy Check If a Matrix is Orthogonal Data Science Parichay Orthogonal Matrix Defi From this definition, we can. In other words, the transpose of an orthogonal. An orthogonal matrix \(u\), from definition 4.11.7, is one in which \(uu^{t} = i\). In particular, taking v = w means that lengths are preserved by orthogonal. A matrix a ∈ gl. An orthogonal matrix is a square matrix whose rows and columns are orthogonal unit vectors. Orthogonal Matrix Defi.
From www.chegg.com
Solved Problem 12 Practice with Orthogonal Matrices Consider Orthogonal Matrix Defi From this definition, we can. A matrix a ∈ gl. N (r) is orthogonal if av · aw = v · w for all vectors v and w. In other words, the transpose of an orthogonal. An orthogonal matrix \(u\), from definition 4.11.7, is one in which \(uu^{t} = i\). An orthogonal matrix is a square matrix a if and. Orthogonal Matrix Defi.
From www.youtube.com
Linear Algebra Matrix Orthogonality YouTube Orthogonal Matrix Defi An orthogonal matrix is a square matrix a if and only its transpose is as same as its inverse. Or we can say when the product of a square matrix and its transpose gives an identity matrix, then the square matrix is known as an. A matrix a ∈ gl. An orthogonal matrix is a square matrix whose rows and. Orthogonal Matrix Defi.
From www.youtube.com
【Orthogonality】06 Orthogonal matrix YouTube Orthogonal Matrix Defi Or we can say when the product of a square matrix and its transpose gives an identity matrix, then the square matrix is known as an. A matrix is called orthogonal matrix when the transpose of matrix is inverse of that matrix or the product of matrix and it’s transpose is. In other words, the transpose of an orthogonal. A. Orthogonal Matrix Defi.
From www.youtube.com
Orthonormal,Orthogonal matrix (EE MATH มทส.) YouTube Orthogonal Matrix Defi From this definition, we can. An orthogonal matrix is a square matrix a if and only its transpose is as same as its inverse. A matrix is called orthogonal matrix when the transpose of matrix is inverse of that matrix or the product of matrix and it’s transpose is. An orthogonal matrix is a square matrix whose rows and columns. Orthogonal Matrix Defi.
From www.slideserve.com
PPT 6.4 Best Approximation; Least Squares PowerPoint Presentation Orthogonal Matrix Defi In particular, taking v = w means that lengths are preserved by orthogonal. An orthogonal matrix \(u\), from definition 4.11.7, is one in which \(uu^{t} = i\). An orthogonal matrix is a square matrix whose rows and columns are orthogonal unit vectors (i.e., orthonormal vectors), meaning that their dot. Or we can say when the product of a square matrix. Orthogonal Matrix Defi.
From www.youtube.com
Orthogonal Matrix /Definition &Example/TN/12th Maths/Chapter1 Orthogonal Matrix Defi A matrix is called orthogonal matrix when the transpose of matrix is inverse of that matrix or the product of matrix and it’s transpose is. In other words, the transpose of an orthogonal. An orthogonal matrix is a square matrix whose rows and columns are orthogonal unit vectors (i.e., orthonormal vectors), meaning that their dot. N (r) is orthogonal if. Orthogonal Matrix Defi.
From www.youtube.com
How to Prove that a Matrix is Orthogonal YouTube Orthogonal Matrix Defi Or we can say when the product of a square matrix and its transpose gives an identity matrix, then the square matrix is known as an. A matrix is called orthogonal matrix when the transpose of matrix is inverse of that matrix or the product of matrix and it’s transpose is. An orthogonal matrix \(u\), from definition 4.11.7, is one. Orthogonal Matrix Defi.
From www.bartleby.com
Answered Orthogonally diagonalize the matrix,… bartleby Orthogonal Matrix Defi A matrix is called orthogonal matrix when the transpose of matrix is inverse of that matrix or the product of matrix and it’s transpose is. In particular, taking v = w means that lengths are preserved by orthogonal. An orthogonal matrix is a square matrix a if and only its transpose is as same as its inverse. An orthogonal matrix. Orthogonal Matrix Defi.
From discourse.mc-stan.org
Efficient orthogonal matrix parameterization Modeling The Stan Forums Orthogonal Matrix Defi In other words, the transpose of an orthogonal. An orthogonal matrix is a square matrix a if and only its transpose is as same as its inverse. An orthogonal matrix is a square matrix whose rows and columns are orthogonal unit vectors (i.e., orthonormal vectors), meaning that their dot. A matrix a ∈ gl. In particular, taking v = w. Orthogonal Matrix Defi.