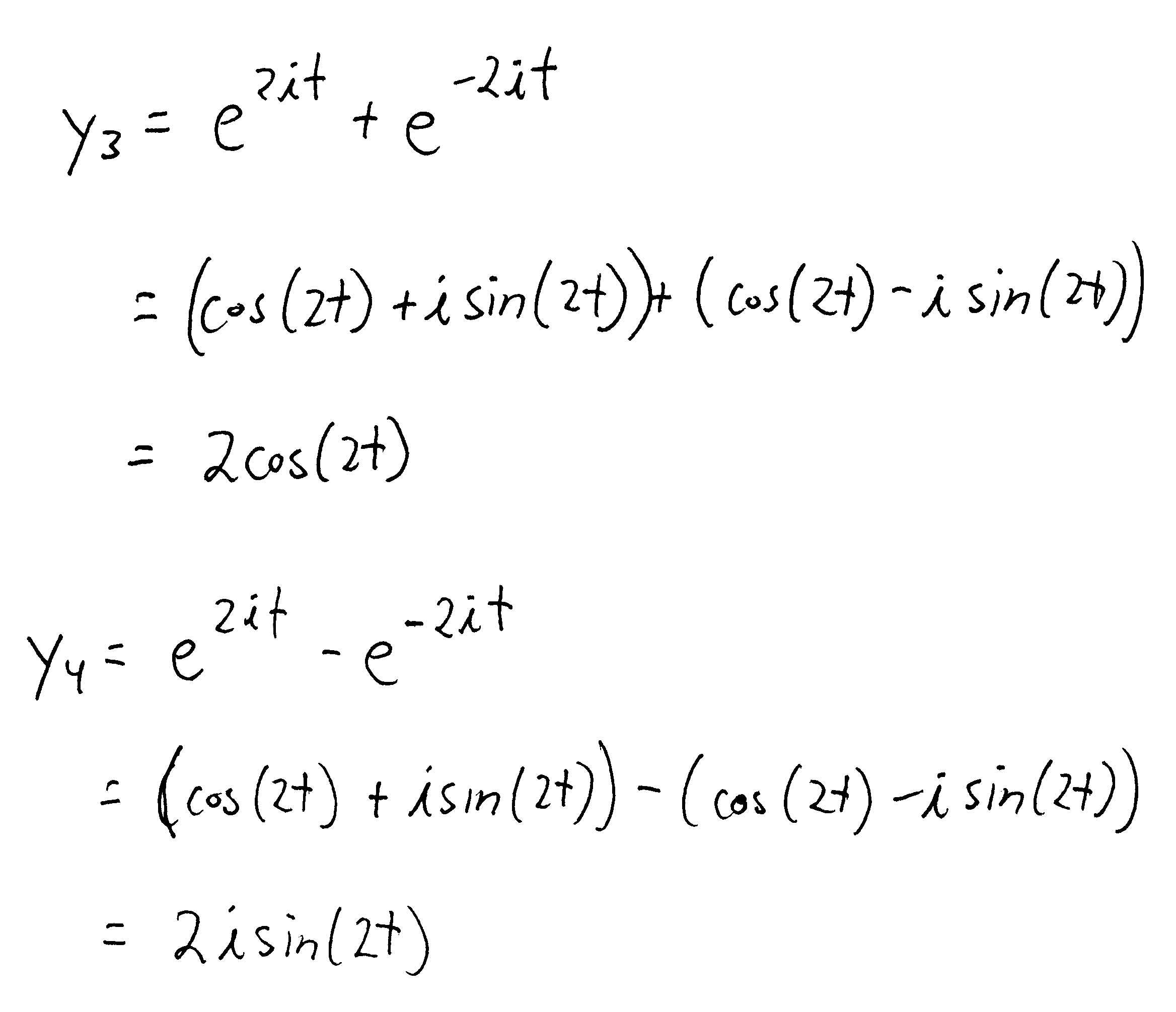Euler Differential Equation Formula . Euler's method assumes our solution is written in the form of a taylor's series. The formula for euler's method is y_ {n+1} = y_n + h f (x_n, y_n). In this section we’ll take a brief look at a fairly simple method for approximating solutions to differential equations. In this section we will discuss how to solve euler’s differential equation, ax^2y'' + bxy' +cy = 0. That is, we'll have a function of the form: `y (x+h)` `~~y (x)+h y' (x)+ (h^2y'' (x))/ (2!)` `+ (h^3y'''. We derive the formulas used by euler’s. Note that while this does not involve a. The improved euler method for solving the initial value problem equation \ref {eq:3.2.1} is based on approximating the. Y_n represents the current value of a point on the solution, and y_ {n+1} is the next value, for an increment in.
from collegeparktutors.com
In this section we’ll take a brief look at a fairly simple method for approximating solutions to differential equations. Note that while this does not involve a. The improved euler method for solving the initial value problem equation \ref {eq:3.2.1} is based on approximating the. Y_n represents the current value of a point on the solution, and y_ {n+1} is the next value, for an increment in. That is, we'll have a function of the form: We derive the formulas used by euler’s. The formula for euler's method is y_ {n+1} = y_n + h f (x_n, y_n). `y (x+h)` `~~y (x)+h y' (x)+ (h^2y'' (x))/ (2!)` `+ (h^3y'''. Euler's method assumes our solution is written in the form of a taylor's series. In this section we will discuss how to solve euler’s differential equation, ax^2y'' + bxy' +cy = 0.
College Park Tutors Blog Differential Equations Solving a second
Euler Differential Equation Formula In this section we will discuss how to solve euler’s differential equation, ax^2y'' + bxy' +cy = 0. We derive the formulas used by euler’s. Note that while this does not involve a. That is, we'll have a function of the form: `y (x+h)` `~~y (x)+h y' (x)+ (h^2y'' (x))/ (2!)` `+ (h^3y'''. Y_n represents the current value of a point on the solution, and y_ {n+1} is the next value, for an increment in. In this section we’ll take a brief look at a fairly simple method for approximating solutions to differential equations. In this section we will discuss how to solve euler’s differential equation, ax^2y'' + bxy' +cy = 0. The improved euler method for solving the initial value problem equation \ref {eq:3.2.1} is based on approximating the. Euler's method assumes our solution is written in the form of a taylor's series. The formula for euler's method is y_ {n+1} = y_n + h f (x_n, y_n).
From www.youtube.com
Euler Method for ODEs YouTube Euler Differential Equation Formula In this section we’ll take a brief look at a fairly simple method for approximating solutions to differential equations. `y (x+h)` `~~y (x)+h y' (x)+ (h^2y'' (x))/ (2!)` `+ (h^3y'''. Note that while this does not involve a. That is, we'll have a function of the form: Euler's method assumes our solution is written in the form of a taylor's. Euler Differential Equation Formula.
From calcworkshop.com
How to do Euler's Method? (Simply Explained in 4 Powerful Examples) Euler Differential Equation Formula Y_n represents the current value of a point on the solution, and y_ {n+1} is the next value, for an increment in. Euler's method assumes our solution is written in the form of a taylor's series. We derive the formulas used by euler’s. The improved euler method for solving the initial value problem equation \ref {eq:3.2.1} is based on approximating. Euler Differential Equation Formula.
From www.youtube.com
Euler's method for differential equations example 1 YouTube Euler Differential Equation Formula That is, we'll have a function of the form: In this section we will discuss how to solve euler’s differential equation, ax^2y'' + bxy' +cy = 0. We derive the formulas used by euler’s. The formula for euler's method is y_ {n+1} = y_n + h f (x_n, y_n). Euler's method assumes our solution is written in the form of. Euler Differential Equation Formula.
From www.youtube.com
Second Order Nonhomogeneous CauchyEuler Differential Equations YouTube Euler Differential Equation Formula We derive the formulas used by euler’s. In this section we’ll take a brief look at a fairly simple method for approximating solutions to differential equations. Euler's method assumes our solution is written in the form of a taylor's series. That is, we'll have a function of the form: Note that while this does not involve a. The formula for. Euler Differential Equation Formula.
From www.bartleby.com
Answered Use Euler's method to solve the… bartleby Euler Differential Equation Formula Euler's method assumes our solution is written in the form of a taylor's series. In this section we’ll take a brief look at a fairly simple method for approximating solutions to differential equations. In this section we will discuss how to solve euler’s differential equation, ax^2y'' + bxy' +cy = 0. `y (x+h)` `~~y (x)+h y' (x)+ (h^2y'' (x))/ (2!)`. Euler Differential Equation Formula.
From www.youtube.com
Higher Order Cauchy Euler Differential Equations Cauchy Euler Euler Differential Equation Formula Euler's method assumes our solution is written in the form of a taylor's series. In this section we’ll take a brief look at a fairly simple method for approximating solutions to differential equations. Note that while this does not involve a. `y (x+h)` `~~y (x)+h y' (x)+ (h^2y'' (x))/ (2!)` `+ (h^3y'''. The formula for euler's method is y_ {n+1}. Euler Differential Equation Formula.
From www.youtube.com
ThirdOrder CauchyEuler Equation. Example. YouTube Euler Differential Equation Formula Euler's method assumes our solution is written in the form of a taylor's series. Note that while this does not involve a. That is, we'll have a function of the form: Y_n represents the current value of a point on the solution, and y_ {n+1} is the next value, for an increment in. `y (x+h)` `~~y (x)+h y' (x)+ (h^2y''. Euler Differential Equation Formula.
From www.youtube.com
Differential Equations Euler's Method YouTube Euler Differential Equation Formula That is, we'll have a function of the form: In this section we will discuss how to solve euler’s differential equation, ax^2y'' + bxy' +cy = 0. Euler's method assumes our solution is written in the form of a taylor's series. Y_n represents the current value of a point on the solution, and y_ {n+1} is the next value, for. Euler Differential Equation Formula.
From sdenisan.blogspot.com
Linear Differential Equation denis Euler Differential Equation Formula In this section we’ll take a brief look at a fairly simple method for approximating solutions to differential equations. Euler's method assumes our solution is written in the form of a taylor's series. That is, we'll have a function of the form: The improved euler method for solving the initial value problem equation \ref {eq:3.2.1} is based on approximating the.. Euler Differential Equation Formula.
From www.youtube.com
Solve the Cauchy Euler Differential Equation x^2y'' 2y = 0 YouTube Euler Differential Equation Formula In this section we will discuss how to solve euler’s differential equation, ax^2y'' + bxy' +cy = 0. Euler's method assumes our solution is written in the form of a taylor's series. The formula for euler's method is y_ {n+1} = y_n + h f (x_n, y_n). `y (x+h)` `~~y (x)+h y' (x)+ (h^2y'' (x))/ (2!)` `+ (h^3y'''. The improved. Euler Differential Equation Formula.
From www.livescience.com
Euler’s Identity 'The Most Beautiful Equation' Live Science Euler Differential Equation Formula That is, we'll have a function of the form: We derive the formulas used by euler’s. `y (x+h)` `~~y (x)+h y' (x)+ (h^2y'' (x))/ (2!)` `+ (h^3y'''. The improved euler method for solving the initial value problem equation \ref {eq:3.2.1} is based on approximating the. In this section we will discuss how to solve euler’s differential equation, ax^2y'' + bxy'. Euler Differential Equation Formula.
From www.youtube.com
CauchyEuler Differential Equation x^2y'' + 2xy' y = 0 YouTube Euler Differential Equation Formula We derive the formulas used by euler’s. In this section we’ll take a brief look at a fairly simple method for approximating solutions to differential equations. In this section we will discuss how to solve euler’s differential equation, ax^2y'' + bxy' +cy = 0. Note that while this does not involve a. The formula for euler's method is y_ {n+1}. Euler Differential Equation Formula.
From www.songho.ca
Euler's Equation Euler Differential Equation Formula We derive the formulas used by euler’s. In this section we will discuss how to solve euler’s differential equation, ax^2y'' + bxy' +cy = 0. Euler's method assumes our solution is written in the form of a taylor's series. That is, we'll have a function of the form: `y (x+h)` `~~y (x)+h y' (x)+ (h^2y'' (x))/ (2!)` `+ (h^3y'''. The. Euler Differential Equation Formula.
From www.coursehero.com
[Solved] . Solve the 2ndorder nonhomogeneous CauchyEuler Equation, x Euler Differential Equation Formula We derive the formulas used by euler’s. In this section we’ll take a brief look at a fairly simple method for approximating solutions to differential equations. That is, we'll have a function of the form: `y (x+h)` `~~y (x)+h y' (x)+ (h^2y'' (x))/ (2!)` `+ (h^3y'''. Y_n represents the current value of a point on the solution, and y_ {n+1}. Euler Differential Equation Formula.
From www.chegg.com
Solved Consider the thirdorder CauchyEuler equation Euler Differential Equation Formula Y_n represents the current value of a point on the solution, and y_ {n+1} is the next value, for an increment in. The formula for euler's method is y_ {n+1} = y_n + h f (x_n, y_n). In this section we will discuss how to solve euler’s differential equation, ax^2y'' + bxy' +cy = 0. We derive the formulas used. Euler Differential Equation Formula.
From collegeparktutors.com
College Park Tutors Blog Differential Equations Solving a second Euler Differential Equation Formula The formula for euler's method is y_ {n+1} = y_n + h f (x_n, y_n). The improved euler method for solving the initial value problem equation \ref {eq:3.2.1} is based on approximating the. In this section we will discuss how to solve euler’s differential equation, ax^2y'' + bxy' +cy = 0. Note that while this does not involve a. In. Euler Differential Equation Formula.
From www.youtube.com
Cauchy Euler Differential Equation Non HomogeneousStep By Step Euler Differential Equation Formula In this section we will discuss how to solve euler’s differential equation, ax^2y'' + bxy' +cy = 0. Note that while this does not involve a. `y (x+h)` `~~y (x)+h y' (x)+ (h^2y'' (x))/ (2!)` `+ (h^3y'''. Euler's method assumes our solution is written in the form of a taylor's series. The improved euler method for solving the initial value. Euler Differential Equation Formula.
From www.semanticscholar.org
[PDF] A Reliable Algorithm For Solving CauchyEuler Differential Euler Differential Equation Formula Euler's method assumes our solution is written in the form of a taylor's series. In this section we’ll take a brief look at a fairly simple method for approximating solutions to differential equations. We derive the formulas used by euler’s. `y (x+h)` `~~y (x)+h y' (x)+ (h^2y'' (x))/ (2!)` `+ (h^3y'''. Y_n represents the current value of a point on. Euler Differential Equation Formula.
From www.studypool.com
SOLUTION Cauchy euler equation Studypool Euler Differential Equation Formula The improved euler method for solving the initial value problem equation \ref {eq:3.2.1} is based on approximating the. Note that while this does not involve a. Y_n represents the current value of a point on the solution, and y_ {n+1} is the next value, for an increment in. That is, we'll have a function of the form: In this section. Euler Differential Equation Formula.
From www.studypool.com
SOLUTION Cauchy euler s differential equations Studypool Euler Differential Equation Formula In this section we will discuss how to solve euler’s differential equation, ax^2y'' + bxy' +cy = 0. That is, we'll have a function of the form: Note that while this does not involve a. The improved euler method for solving the initial value problem equation \ref {eq:3.2.1} is based on approximating the. In this section we’ll take a brief. Euler Differential Equation Formula.
From collegeparktutors.com
College Park Tutors Blog Differential Equations Solving a second Euler Differential Equation Formula In this section we’ll take a brief look at a fairly simple method for approximating solutions to differential equations. `y (x+h)` `~~y (x)+h y' (x)+ (h^2y'' (x))/ (2!)` `+ (h^3y'''. In this section we will discuss how to solve euler’s differential equation, ax^2y'' + bxy' +cy = 0. The formula for euler's method is y_ {n+1} = y_n + h. Euler Differential Equation Formula.
From www.youtube.com
Lecture 19 CauchyEuler Differential Equation Differential Equations Euler Differential Equation Formula Note that while this does not involve a. Y_n represents the current value of a point on the solution, and y_ {n+1} is the next value, for an increment in. Euler's method assumes our solution is written in the form of a taylor's series. In this section we will discuss how to solve euler’s differential equation, ax^2y'' + bxy' +cy. Euler Differential Equation Formula.
From www.slideserve.com
PPT Euler’s Equation PowerPoint Presentation, free download ID324004 Euler Differential Equation Formula In this section we will discuss how to solve euler’s differential equation, ax^2y'' + bxy' +cy = 0. Note that while this does not involve a. `y (x+h)` `~~y (x)+h y' (x)+ (h^2y'' (x))/ (2!)` `+ (h^3y'''. The formula for euler's method is y_ {n+1} = y_n + h f (x_n, y_n). That is, we'll have a function of the. Euler Differential Equation Formula.
From muthu.co
Deriving the famous Euler’s formula through Taylor Series Muthukrishnan Euler Differential Equation Formula That is, we'll have a function of the form: The improved euler method for solving the initial value problem equation \ref {eq:3.2.1} is based on approximating the. In this section we will discuss how to solve euler’s differential equation, ax^2y'' + bxy' +cy = 0. We derive the formulas used by euler’s. In this section we’ll take a brief look. Euler Differential Equation Formula.
From peachyfileson.cf
Differential equations by m d raisinghania Euler Differential Equation Formula In this section we’ll take a brief look at a fairly simple method for approximating solutions to differential equations. In this section we will discuss how to solve euler’s differential equation, ax^2y'' + bxy' +cy = 0. `y (x+h)` `~~y (x)+h y' (x)+ (h^2y'' (x))/ (2!)` `+ (h^3y'''. The improved euler method for solving the initial value problem equation \ref. Euler Differential Equation Formula.
From andymath.com
Euler's Formula Euler Differential Equation Formula The improved euler method for solving the initial value problem equation \ref {eq:3.2.1} is based on approximating the. The formula for euler's method is y_ {n+1} = y_n + h f (x_n, y_n). Y_n represents the current value of a point on the solution, and y_ {n+1} is the next value, for an increment in. Note that while this does. Euler Differential Equation Formula.
From www.youtube.com
Cauchy Euler Equations Problem 2 (Differential Equations) YouTube Euler Differential Equation Formula That is, we'll have a function of the form: The improved euler method for solving the initial value problem equation \ref {eq:3.2.1} is based on approximating the. Euler's method assumes our solution is written in the form of a taylor's series. The formula for euler's method is y_ {n+1} = y_n + h f (x_n, y_n). We derive the formulas. Euler Differential Equation Formula.
From www.youtube.com
7. Modified Euler's Method Problem1 Numerical Solution of Ordinary Euler Differential Equation Formula We derive the formulas used by euler’s. The formula for euler's method is y_ {n+1} = y_n + h f (x_n, y_n). The improved euler method for solving the initial value problem equation \ref {eq:3.2.1} is based on approximating the. That is, we'll have a function of the form: Note that while this does not involve a. In this section. Euler Differential Equation Formula.
From www.youtube.com
Cauchy Euler's Homogeneous Linear Differential Equation 2 (with Euler Differential Equation Formula Note that while this does not involve a. In this section we’ll take a brief look at a fairly simple method for approximating solutions to differential equations. The improved euler method for solving the initial value problem equation \ref {eq:3.2.1} is based on approximating the. The formula for euler's method is y_ {n+1} = y_n + h f (x_n, y_n).. Euler Differential Equation Formula.
From www.semanticscholar.org
[PDF] A THIRD ORDER EULER METHOD FOR NUMERICAL SOLUTION OF ORDINARY Euler Differential Equation Formula In this section we will discuss how to solve euler’s differential equation, ax^2y'' + bxy' +cy = 0. Y_n represents the current value of a point on the solution, and y_ {n+1} is the next value, for an increment in. The improved euler method for solving the initial value problem equation \ref {eq:3.2.1} is based on approximating the. We derive. Euler Differential Equation Formula.
From www.grc.nasa.gov
Euler Equations Euler Differential Equation Formula The improved euler method for solving the initial value problem equation \ref {eq:3.2.1} is based on approximating the. In this section we will discuss how to solve euler’s differential equation, ax^2y'' + bxy' +cy = 0. Euler's method assumes our solution is written in the form of a taylor's series. `y (x+h)` `~~y (x)+h y' (x)+ (h^2y'' (x))/ (2!)` `+. Euler Differential Equation Formula.
From www.slideserve.com
PPT Maple for Lagrangian Mechanics PowerPoint Presentation ID631668 Euler Differential Equation Formula That is, we'll have a function of the form: The formula for euler's method is y_ {n+1} = y_n + h f (x_n, y_n). The improved euler method for solving the initial value problem equation \ref {eq:3.2.1} is based on approximating the. Y_n represents the current value of a point on the solution, and y_ {n+1} is the next value,. Euler Differential Equation Formula.
From www.youtube.com
CauchyEuler Differential Equations (2nd Order) YouTube Euler Differential Equation Formula The formula for euler's method is y_ {n+1} = y_n + h f (x_n, y_n). That is, we'll have a function of the form: Note that while this does not involve a. Euler's method assumes our solution is written in the form of a taylor's series. In this section we’ll take a brief look at a fairly simple method for. Euler Differential Equation Formula.
From www.grc.nasa.gov
Euler Equations Euler Differential Equation Formula The formula for euler's method is y_ {n+1} = y_n + h f (x_n, y_n). Note that while this does not involve a. The improved euler method for solving the initial value problem equation \ref {eq:3.2.1} is based on approximating the. That is, we'll have a function of the form: Y_n represents the current value of a point on the. Euler Differential Equation Formula.
From www.youtube.com
Cauchy Euler Differential Equation t^2y'' + 4ty' + 2y = 0 YouTube Euler Differential Equation Formula We derive the formulas used by euler’s. Euler's method assumes our solution is written in the form of a taylor's series. In this section we’ll take a brief look at a fairly simple method for approximating solutions to differential equations. Note that while this does not involve a. The improved euler method for solving the initial value problem equation \ref. Euler Differential Equation Formula.