Math Definition Of Interior Points at Werner Obrien blog

Math Definition Of Interior Points. Interior points, boundary points, open and closed sets. Let (x, d) be a metric space with distance d: A point x0 ∈ d ⊂ x is called an interior point in d if there is a. In mathematics, the interior of a set refers to the collection of all points that can be surrounded by a neighborhood entirely contained within that set. We write $\mathring a$ to denote the interior of $a$. X × x → [0, ∞). In mathematics, particularly in geometry and topology, interior points refer to the points that lie within the boundaries of a set or a region. Any open neighborhood of a boundary point contains an interior point and an exterior point. Let (x, τ) be a topological space and let a ⊆ x. The interior of a a is the union of all open subsets of. The interior of $a$ is the union of all open subsets of $a$. A point a ∈ a is called an interior point of a if there exists an open neighbourhood () of such. Let $a$ denote a subset of a topological space $x$. In other words let (x, τ) (x, τ) be a topological space and a a be a subset of x x.

X × x → [0, ∞). The interior of a a is the union of all open subsets of. In other words let (x, τ) (x, τ) be a topological space and a a be a subset of x x. The interior of $a$ is the union of all open subsets of $a$. Interior points, boundary points, open and closed sets. In mathematics, the interior of a set refers to the collection of all points that can be surrounded by a neighborhood entirely contained within that set. A point a ∈ a is called an interior point of a if there exists an open neighbourhood () of such. Let (x, τ) be a topological space and let a ⊆ x. In mathematics, particularly in geometry and topology, interior points refer to the points that lie within the boundaries of a set or a region. We write $\mathring a$ to denote the interior of $a$.

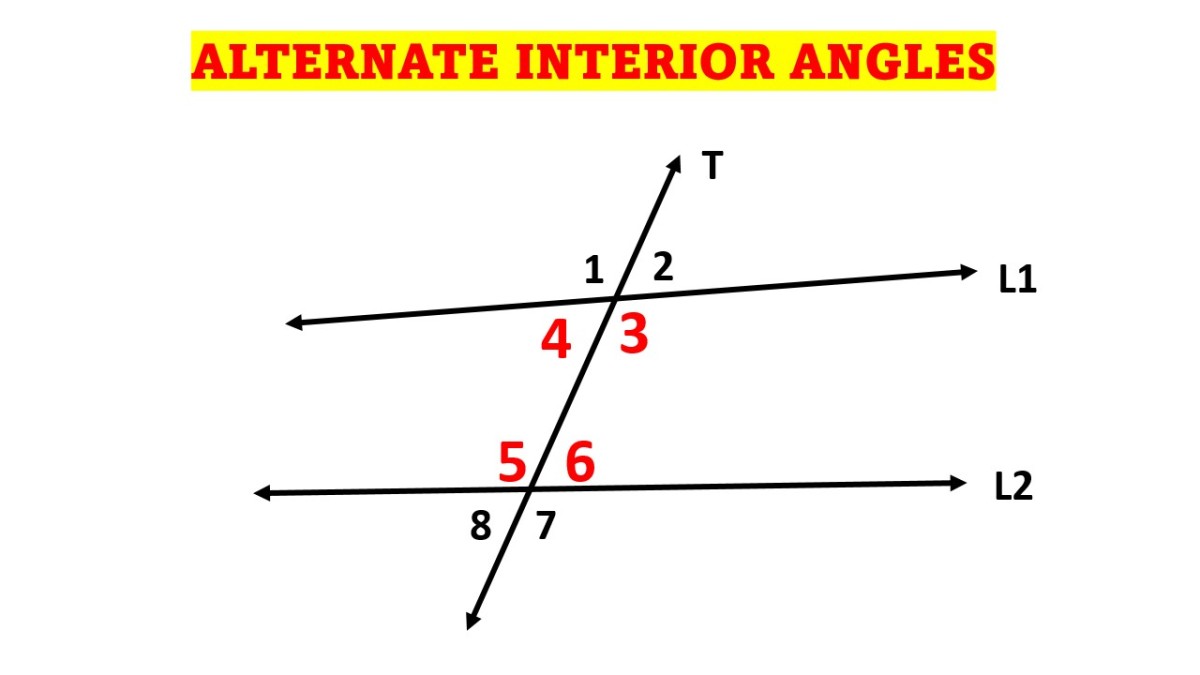
Alternate Interior Angles Examples, Definition, Theorem » Education Tips

Math Definition Of Interior Points We write $\mathring a$ to denote the interior of $a$. In mathematics, the interior of a set refers to the collection of all points that can be surrounded by a neighborhood entirely contained within that set. The interior of $a$ is the union of all open subsets of $a$. In other words let (x, τ) (x, τ) be a topological space and a a be a subset of x x. Let (x, τ) be a topological space and let a ⊆ x. Let (x, d) be a metric space with distance d: A point x0 ∈ d ⊂ x is called an interior point in d if there is a. Interior points, boundary points, open and closed sets. Any open neighborhood of a boundary point contains an interior point and an exterior point. Let $a$ denote a subset of a topological space $x$. A point a ∈ a is called an interior point of a if there exists an open neighbourhood () of such. We write $\mathring a$ to denote the interior of $a$. X × x → [0, ∞). In mathematics, particularly in geometry and topology, interior points refer to the points that lie within the boundaries of a set or a region. The interior of a a is the union of all open subsets of.