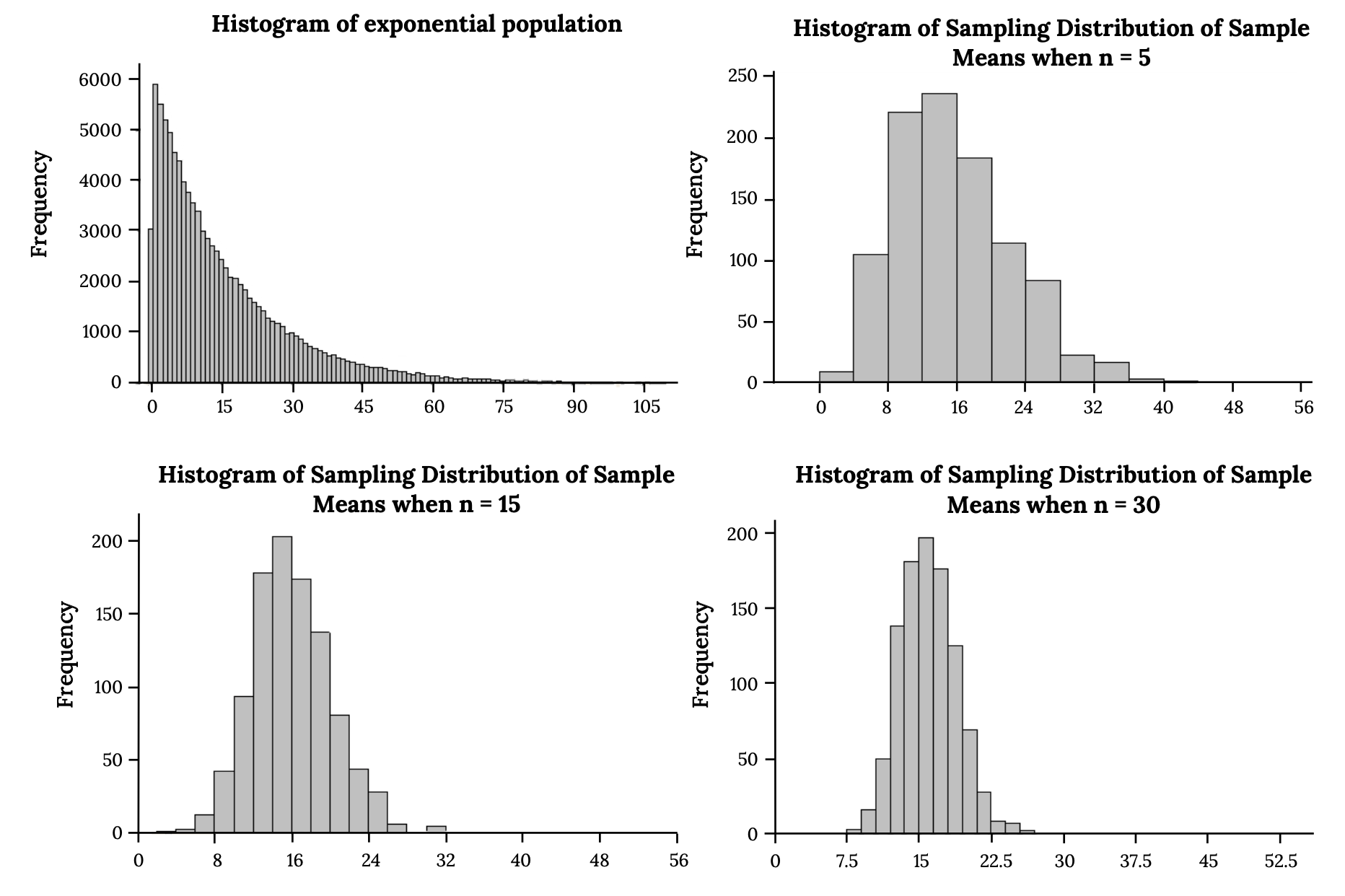
Distribution Sample Mean . A sampling distribution of a statistic is a type of probability distribution created by drawing many random samples of a given size from the same population. The standard deviation of the sample means is. The sampling distribution is the probability distribution of a statistic, such as the mean or variance, derived from multiple. The sample mean is a random variable; As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. The mean of the sampling distribution of the mean is the mean of the population from which the scores were. The mean of the distribution of the sample means is [latex]\mu_{\overline{x}}=34[/latex]. To demonstrate the sampling distribution, let’s start with obtaining all of the possible samples of size \ (n=2\) from the populations, sampling without replacement.
from pressbooks.lib.vt.edu
To demonstrate the sampling distribution, let’s start with obtaining all of the possible samples of size \ (n=2\) from the populations, sampling without replacement. A sampling distribution of a statistic is a type of probability distribution created by drawing many random samples of a given size from the same population. The mean of the sampling distribution of the mean is the mean of the population from which the scores were. The standard deviation of the sample means is. As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. The sampling distribution is the probability distribution of a statistic, such as the mean or variance, derived from multiple. The sample mean is a random variable; The mean of the distribution of the sample means is [latex]\mu_{\overline{x}}=34[/latex].
6.2 The Sampling Distribution of the Sample Mean (σ Known
Distribution Sample Mean A sampling distribution of a statistic is a type of probability distribution created by drawing many random samples of a given size from the same population. To demonstrate the sampling distribution, let’s start with obtaining all of the possible samples of size \ (n=2\) from the populations, sampling without replacement. The sampling distribution is the probability distribution of a statistic, such as the mean or variance, derived from multiple. The mean of the distribution of the sample means is [latex]\mu_{\overline{x}}=34[/latex]. As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. The sample mean is a random variable; The mean of the sampling distribution of the mean is the mean of the population from which the scores were. A sampling distribution of a statistic is a type of probability distribution created by drawing many random samples of a given size from the same population. The standard deviation of the sample means is.
From www.statology.org
How to Calculate Sampling Distributions in R Distribution Sample Mean The sample mean is a random variable; As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. A sampling distribution of a statistic is a type of probability distribution created by drawing many random samples of a given size from the same population. To demonstrate the sampling distribution, let’s start with obtaining all of the possible. Distribution Sample Mean.
From open.maricopa.edu
Chapter 8 Sampling Distributions Introduction to Statistics for Distribution Sample Mean To demonstrate the sampling distribution, let’s start with obtaining all of the possible samples of size \ (n=2\) from the populations, sampling without replacement. The mean of the distribution of the sample means is [latex]\mu_{\overline{x}}=34[/latex]. As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. A sampling distribution of a statistic is a type of probability. Distribution Sample Mean.
From www.slideserve.com
PPT Properties of the Sampling Distribution of x PowerPoint Distribution Sample Mean The sampling distribution is the probability distribution of a statistic, such as the mean or variance, derived from multiple. A sampling distribution of a statistic is a type of probability distribution created by drawing many random samples of a given size from the same population. The mean of the sampling distribution of the mean is the mean of the population. Distribution Sample Mean.
From www.slideserve.com
PPT SAMPLE MEAN and its distribution PowerPoint Presentation, free Distribution Sample Mean The sample mean is a random variable; The sampling distribution is the probability distribution of a statistic, such as the mean or variance, derived from multiple. The standard deviation of the sample means is. A sampling distribution of a statistic is a type of probability distribution created by drawing many random samples of a given size from the same population.. Distribution Sample Mean.
From spot.pcc.edu
Sampling distribution of a sample mean Distribution Sample Mean The mean of the sampling distribution of the mean is the mean of the population from which the scores were. The standard deviation of the sample means is. To demonstrate the sampling distribution, let’s start with obtaining all of the possible samples of size \ (n=2\) from the populations, sampling without replacement. The mean of the distribution of the sample. Distribution Sample Mean.
From www.slideshare.net
Normal distribution and sampling distribution Distribution Sample Mean As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. The mean of the sampling distribution of the mean is the mean of the population from which the scores were. The sample mean is a random variable; The sampling distribution is the probability distribution of a statistic, such as the mean or variance, derived from multiple.. Distribution Sample Mean.
From www.youtube.com
Calculating probability involving the sampling distribution of the Distribution Sample Mean To demonstrate the sampling distribution, let’s start with obtaining all of the possible samples of size \ (n=2\) from the populations, sampling without replacement. The standard deviation of the sample means is. The sampling distribution is the probability distribution of a statistic, such as the mean or variance, derived from multiple. As such it is written \(\bar{x}\), and \(\bar{x}\) stands. Distribution Sample Mean.
From www.cqeacademy.com
Point Estimates and Confidence Intervals CQE Academy Distribution Sample Mean As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. A sampling distribution of a statistic is a type of probability distribution created by drawing many random samples of a given size from the same population. The mean of the sampling distribution of the mean is the mean of the population from which the scores were.. Distribution Sample Mean.
From www.chegg.com
Solved Sampling Distribution of the Mean Difference Distribution Sample Mean A sampling distribution of a statistic is a type of probability distribution created by drawing many random samples of a given size from the same population. The standard deviation of the sample means is. The mean of the distribution of the sample means is [latex]\mu_{\overline{x}}=34[/latex]. The mean of the sampling distribution of the mean is the mean of the population. Distribution Sample Mean.
From www.slideserve.com
PPT Sampling Methods and the Central Limit Theorem PowerPoint Distribution Sample Mean The mean of the distribution of the sample means is [latex]\mu_{\overline{x}}=34[/latex]. To demonstrate the sampling distribution, let’s start with obtaining all of the possible samples of size \ (n=2\) from the populations, sampling without replacement. The mean of the sampling distribution of the mean is the mean of the population from which the scores were. The sample mean is a. Distribution Sample Mean.
From www.researchgate.net
The effect of sample size on the sampling distribution. As the size of Distribution Sample Mean The mean of the sampling distribution of the mean is the mean of the population from which the scores were. The mean of the distribution of the sample means is [latex]\mu_{\overline{x}}=34[/latex]. The standard deviation of the sample means is. The sample mean is a random variable; A sampling distribution of a statistic is a type of probability distribution created by. Distribution Sample Mean.
From www.youtube.com
FINDING THE MEAN AND VARIANCE OF THE SAMPLING DISTRIBUTION OF SAMPLE Distribution Sample Mean The sample mean is a random variable; As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. To demonstrate the sampling distribution, let’s start with obtaining all of the possible samples of size \ (n=2\) from the populations, sampling without replacement. The mean of the sampling distribution of the mean is the mean of the population. Distribution Sample Mean.
From www.slideserve.com
PPT Sampling Distribution of the Mean PowerPoint Presentation, free Distribution Sample Mean The standard deviation of the sample means is. A sampling distribution of a statistic is a type of probability distribution created by drawing many random samples of a given size from the same population. The mean of the sampling distribution of the mean is the mean of the population from which the scores were. The sample mean is a random. Distribution Sample Mean.
From saylordotorg.github.io
The Sampling Distribution of the Sample Mean Distribution Sample Mean The mean of the distribution of the sample means is [latex]\mu_{\overline{x}}=34[/latex]. The standard deviation of the sample means is. A sampling distribution of a statistic is a type of probability distribution created by drawing many random samples of a given size from the same population. To demonstrate the sampling distribution, let’s start with obtaining all of the possible samples of. Distribution Sample Mean.
From www.youtube.com
Sampling distribution of the sample means (Normal distribution Distribution Sample Mean The mean of the sampling distribution of the mean is the mean of the population from which the scores were. The standard deviation of the sample means is. As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. The sample mean is a random variable; A sampling distribution of a statistic is a type of probability. Distribution Sample Mean.
From www.coursehero.com
[Solved] Find the mean of the sampling distribution of sample means Distribution Sample Mean As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. The mean of the distribution of the sample means is [latex]\mu_{\overline{x}}=34[/latex]. The sampling distribution is the probability distribution of a statistic, such as the mean or variance, derived from multiple. The mean of the sampling distribution of the mean is the mean of the population from. Distribution Sample Mean.
From www.upgrad.com
Properties of Sampling Distributions Explained in Statistics upGrad Learn Distribution Sample Mean The sampling distribution is the probability distribution of a statistic, such as the mean or variance, derived from multiple. To demonstrate the sampling distribution, let’s start with obtaining all of the possible samples of size \ (n=2\) from the populations, sampling without replacement. The standard deviation of the sample means is. The sample mean is a random variable; A sampling. Distribution Sample Mean.
From faculty.nps.edu
Chapter 9 Introduction to Sampling Distributions Introduction to Distribution Sample Mean The standard deviation of the sample means is. The sample mean is a random variable; The mean of the distribution of the sample means is [latex]\mu_{\overline{x}}=34[/latex]. To demonstrate the sampling distribution, let’s start with obtaining all of the possible samples of size \ (n=2\) from the populations, sampling without replacement. As such it is written \(\bar{x}\), and \(\bar{x}\) stands for. Distribution Sample Mean.
From www.slideserve.com
PPT Chapter 17 PowerPoint Presentation, free download ID3422491 Distribution Sample Mean To demonstrate the sampling distribution, let’s start with obtaining all of the possible samples of size \ (n=2\) from the populations, sampling without replacement. The sample mean is a random variable; The sampling distribution is the probability distribution of a statistic, such as the mean or variance, derived from multiple. The mean of the sampling distribution of the mean is. Distribution Sample Mean.
From www.slideserve.com
PPT Sampling Distribution of a Sample Mean PowerPoint Presentation Distribution Sample Mean The sampling distribution is the probability distribution of a statistic, such as the mean or variance, derived from multiple. The mean of the sampling distribution of the mean is the mean of the population from which the scores were. The mean of the distribution of the sample means is [latex]\mu_{\overline{x}}=34[/latex]. The standard deviation of the sample means is. A sampling. Distribution Sample Mean.
From kassidydesnhsimmons.blogspot.com
Measures Used to Describe the Sample Distribution Distribution Sample Mean The sample mean is a random variable; To demonstrate the sampling distribution, let’s start with obtaining all of the possible samples of size \ (n=2\) from the populations, sampling without replacement. The mean of the sampling distribution of the mean is the mean of the population from which the scores were. As such it is written \(\bar{x}\), and \(\bar{x}\) stands. Distribution Sample Mean.
From www.animalia-life.club
Z Score Formula For Sample Mean Distribution Sample Mean The mean of the sampling distribution of the mean is the mean of the population from which the scores were. The mean of the distribution of the sample means is [latex]\mu_{\overline{x}}=34[/latex]. As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. To demonstrate the sampling distribution, let’s start with obtaining all of the possible samples of. Distribution Sample Mean.
From www.youtube.com
Finding the Mean and Variance of the sampling distribution of a sample Distribution Sample Mean The mean of the sampling distribution of the mean is the mean of the population from which the scores were. To demonstrate the sampling distribution, let’s start with obtaining all of the possible samples of size \ (n=2\) from the populations, sampling without replacement. A sampling distribution of a statistic is a type of probability distribution created by drawing many. Distribution Sample Mean.
From www.slideserve.com
PPT The Normal Probability Distribution and the Central Limit Theorem Distribution Sample Mean A sampling distribution of a statistic is a type of probability distribution created by drawing many random samples of a given size from the same population. The standard deviation of the sample means is. To demonstrate the sampling distribution, let’s start with obtaining all of the possible samples of size \ (n=2\) from the populations, sampling without replacement. The sampling. Distribution Sample Mean.
From learningschoolenrichifa.z22.web.core.windows.net
Sample Distribution And Sampling Distribution Distribution Sample Mean To demonstrate the sampling distribution, let’s start with obtaining all of the possible samples of size \ (n=2\) from the populations, sampling without replacement. The mean of the sampling distribution of the mean is the mean of the population from which the scores were. As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. The mean. Distribution Sample Mean.
From online.stat.psu.edu
Lesson 4 Sampling Distributions Distribution Sample Mean The sample mean is a random variable; As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. The mean of the distribution of the sample means is [latex]\mu_{\overline{x}}=34[/latex]. The standard deviation of the sample means is. A sampling distribution of a statistic is a type of probability distribution created by drawing many random samples of a. Distribution Sample Mean.
From ecampusontario.pressbooks.pub
6.2 The Sampling Distribution of the Sample Mean (σ Known) MATH 1260 Distribution Sample Mean The sampling distribution is the probability distribution of a statistic, such as the mean or variance, derived from multiple. The mean of the sampling distribution of the mean is the mean of the population from which the scores were. A sampling distribution of a statistic is a type of probability distribution created by drawing many random samples of a given. Distribution Sample Mean.
From www.youtube.com
Chapter 7.2 "Sampling Distribution of the Sample Mean" YouTube Distribution Sample Mean The standard deviation of the sample means is. A sampling distribution of a statistic is a type of probability distribution created by drawing many random samples of a given size from the same population. The mean of the distribution of the sample means is [latex]\mu_{\overline{x}}=34[/latex]. To demonstrate the sampling distribution, let’s start with obtaining all of the possible samples of. Distribution Sample Mean.
From www.slideserve.com
PPT CHAPTER 11 Sampling Distributions PowerPoint Presentation, free Distribution Sample Mean The mean of the distribution of the sample means is [latex]\mu_{\overline{x}}=34[/latex]. To demonstrate the sampling distribution, let’s start with obtaining all of the possible samples of size \ (n=2\) from the populations, sampling without replacement. The sampling distribution is the probability distribution of a statistic, such as the mean or variance, derived from multiple. The standard deviation of the sample. Distribution Sample Mean.
From www.youtube.com
Sampling distribution of the sample mean Probability and Statistics Distribution Sample Mean The sampling distribution is the probability distribution of a statistic, such as the mean or variance, derived from multiple. The standard deviation of the sample means is. To demonstrate the sampling distribution, let’s start with obtaining all of the possible samples of size \ (n=2\) from the populations, sampling without replacement. As such it is written \(\bar{x}\), and \(\bar{x}\) stands. Distribution Sample Mean.
From saylordotorg.github.io
The Sampling Distribution of the Sample Mean Distribution Sample Mean To demonstrate the sampling distribution, let’s start with obtaining all of the possible samples of size \ (n=2\) from the populations, sampling without replacement. The sampling distribution is the probability distribution of a statistic, such as the mean or variance, derived from multiple. As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. The standard deviation. Distribution Sample Mean.
From haldaneolubanke.blogspot.com
52+ mean of the distribution of sample means calculator HaldaneOlubanke Distribution Sample Mean The sample mean is a random variable; The mean of the distribution of the sample means is [latex]\mu_{\overline{x}}=34[/latex]. The standard deviation of the sample means is. The sampling distribution is the probability distribution of a statistic, such as the mean or variance, derived from multiple. The mean of the sampling distribution of the mean is the mean of the population. Distribution Sample Mean.
From pressbooks.lib.vt.edu
6.2 The Sampling Distribution of the Sample Mean (σ Known Distribution Sample Mean The sample mean is a random variable; The standard deviation of the sample means is. The mean of the distribution of the sample means is [latex]\mu_{\overline{x}}=34[/latex]. To demonstrate the sampling distribution, let’s start with obtaining all of the possible samples of size \ (n=2\) from the populations, sampling without replacement. The sampling distribution is the probability distribution of a statistic,. Distribution Sample Mean.
From www.slideserve.com
PPT Chapter 5 Sampling Distributions PowerPoint Presentation, free Distribution Sample Mean To demonstrate the sampling distribution, let’s start with obtaining all of the possible samples of size \ (n=2\) from the populations, sampling without replacement. A sampling distribution of a statistic is a type of probability distribution created by drawing many random samples of a given size from the same population. The sampling distribution is the probability distribution of a statistic,. Distribution Sample Mean.
From www.slideserve.com
PPT Normal Probability Distributions PowerPoint Presentation, free Distribution Sample Mean As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. A sampling distribution of a statistic is a type of probability distribution created by drawing many random samples of a given size from the same population. The mean of the distribution of the sample means is [latex]\mu_{\overline{x}}=34[/latex]. The mean of the sampling distribution of the mean. Distribution Sample Mean.