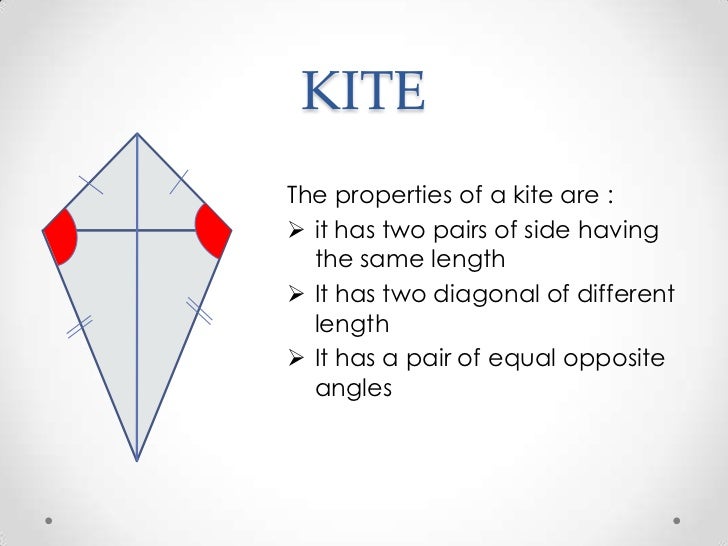
Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1 . In a kite, the diagonals are perpendicular bisectors of each other, with one diagonal being the angle bisector of the opposite angles. D_2$ are lengths of diagonals. Solution for compare the properties of the diagonals of a kite with those of a square Compare the properties of the diagonals of a kite with those of a square. The area of kite $= \frac{1}{2} \times d_1 \times d_2$, where $d_1,\; Properties of a kite perpendicular diagonals the diagonals of a kite are perpendicular to each other. Perimeter of a kite with sides a and b is given by $2\left[a+b\right]$. Study with quizlet and memorize flashcards containing terms like what do the diagonals have to do with each other?, why are there right. We have the right solution;
from www.slideshare.net
Properties of a kite perpendicular diagonals the diagonals of a kite are perpendicular to each other. D_2$ are lengths of diagonals. Compare the properties of the diagonals of a kite with those of a square. Solution for compare the properties of the diagonals of a kite with those of a square The area of kite $= \frac{1}{2} \times d_1 \times d_2$, where $d_1,\; Study with quizlet and memorize flashcards containing terms like what do the diagonals have to do with each other?, why are there right. We have the right solution; Perimeter of a kite with sides a and b is given by $2\left[a+b\right]$. In a kite, the diagonals are perpendicular bisectors of each other, with one diagonal being the angle bisector of the opposite angles.
Quadrilateral
Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1 The area of kite $= \frac{1}{2} \times d_1 \times d_2$, where $d_1,\; Solution for compare the properties of the diagonals of a kite with those of a square Perimeter of a kite with sides a and b is given by $2\left[a+b\right]$. We have the right solution; In a kite, the diagonals are perpendicular bisectors of each other, with one diagonal being the angle bisector of the opposite angles. Study with quizlet and memorize flashcards containing terms like what do the diagonals have to do with each other?, why are there right. D_2$ are lengths of diagonals. The area of kite $= \frac{1}{2} \times d_1 \times d_2$, where $d_1,\; Compare the properties of the diagonals of a kite with those of a square. Properties of a kite perpendicular diagonals the diagonals of a kite are perpendicular to each other.
From www.youtube.com
Proof The diagonals of a kite are perpendicular YouTube Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1 In a kite, the diagonals are perpendicular bisectors of each other, with one diagonal being the angle bisector of the opposite angles. Solution for compare the properties of the diagonals of a kite with those of a square Properties of a kite perpendicular diagonals the diagonals of a kite are perpendicular to each other. We have the right solution; The. Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1.
From byjus.com
What is the Area of a Kite? (Definition, Examples) BYJUS Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1 The area of kite $= \frac{1}{2} \times d_1 \times d_2$, where $d_1,\; We have the right solution; D_2$ are lengths of diagonals. Solution for compare the properties of the diagonals of a kite with those of a square In a kite, the diagonals are perpendicular bisectors of each other, with one diagonal being the angle bisector of the opposite angles.. Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1.
From exoswmvur.blob.core.windows.net
Compare The Properties Of The Diagonals Of A Kite With Those Of A Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1 Properties of a kite perpendicular diagonals the diagonals of a kite are perpendicular to each other. Solution for compare the properties of the diagonals of a kite with those of a square Compare the properties of the diagonals of a kite with those of a square. In a kite, the diagonals are perpendicular bisectors of each other, with one diagonal. Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1.
From exoswmvur.blob.core.windows.net
Compare The Properties Of The Diagonals Of A Kite With Those Of A Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1 In a kite, the diagonals are perpendicular bisectors of each other, with one diagonal being the angle bisector of the opposite angles. Perimeter of a kite with sides a and b is given by $2\left[a+b\right]$. D_2$ are lengths of diagonals. Compare the properties of the diagonals of a kite with those of a square. The area of kite $= \frac{1}{2}. Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1.
From quizlet.com
Prove that the diagonals of a kite are perpendicular to each Quizlet Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1 We have the right solution; D_2$ are lengths of diagonals. Perimeter of a kite with sides a and b is given by $2\left[a+b\right]$. Compare the properties of the diagonals of a kite with those of a square. Study with quizlet and memorize flashcards containing terms like what do the diagonals have to do with each other?, why are there right.. Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1.
From quizlet.com
Explain how to construct a kite, given its diagonals. Quizlet Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1 Perimeter of a kite with sides a and b is given by $2\left[a+b\right]$. Properties of a kite perpendicular diagonals the diagonals of a kite are perpendicular to each other. D_2$ are lengths of diagonals. Study with quizlet and memorize flashcards containing terms like what do the diagonals have to do with each other?, why are there right. We have the. Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1.
From animalia-life.club
Diagonals Of A Square Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1 Compare the properties of the diagonals of a kite with those of a square. Solution for compare the properties of the diagonals of a kite with those of a square The area of kite $= \frac{1}{2} \times d_1 \times d_2$, where $d_1,\; Properties of a kite perpendicular diagonals the diagonals of a kite are perpendicular to each other. D_2$ are. Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1.
From exoswmvur.blob.core.windows.net
Compare The Properties Of The Diagonals Of A Kite With Those Of A Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1 Perimeter of a kite with sides a and b is given by $2\left[a+b\right]$. The area of kite $= \frac{1}{2} \times d_1 \times d_2$, where $d_1,\; D_2$ are lengths of diagonals. Solution for compare the properties of the diagonals of a kite with those of a square Compare the properties of the diagonals of a kite with those of a square.. Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1.
From www.shutterstock.com
Properties Diagonals Kite Stock Vector (Royalty Free) 1950458860 Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1 Solution for compare the properties of the diagonals of a kite with those of a square D_2$ are lengths of diagonals. Perimeter of a kite with sides a and b is given by $2\left[a+b\right]$. The area of kite $= \frac{1}{2} \times d_1 \times d_2$, where $d_1,\; Compare the properties of the diagonals of a kite with those of a square.. Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1.
From ar.inspiredpencil.com
Perpendicular Diagonals Square Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1 D_2$ are lengths of diagonals. Study with quizlet and memorize flashcards containing terms like what do the diagonals have to do with each other?, why are there right. We have the right solution; In a kite, the diagonals are perpendicular bisectors of each other, with one diagonal being the angle bisector of the opposite angles. Solution for compare the properties. Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1.
From goodttorials.blogspot.com
How To Find Missing Angles Of A Kite Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1 Properties of a kite perpendicular diagonals the diagonals of a kite are perpendicular to each other. The area of kite $= \frac{1}{2} \times d_1 \times d_2$, where $d_1,\; We have the right solution; Solution for compare the properties of the diagonals of a kite with those of a square In a kite, the diagonals are perpendicular bisectors of each other,. Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1.
From exoswmvur.blob.core.windows.net
Compare The Properties Of The Diagonals Of A Kite With Those Of A Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1 D_2$ are lengths of diagonals. Solution for compare the properties of the diagonals of a kite with those of a square In a kite, the diagonals are perpendicular bisectors of each other, with one diagonal being the angle bisector of the opposite angles. We have the right solution; The area of kite $= \frac{1}{2} \times d_1 \times d_2$, where $d_1,\;. Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1.
From byjus.com
Show that the diagonals of a square are equal and bisect each other at Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1 Properties of a kite perpendicular diagonals the diagonals of a kite are perpendicular to each other. We have the right solution; Perimeter of a kite with sides a and b is given by $2\left[a+b\right]$. Study with quizlet and memorize flashcards containing terms like what do the diagonals have to do with each other?, why are there right. Solution for compare. Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1.
From ar.inspiredpencil.com
Kite Geometry Angles Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1 Study with quizlet and memorize flashcards containing terms like what do the diagonals have to do with each other?, why are there right. We have the right solution; D_2$ are lengths of diagonals. Compare the properties of the diagonals of a kite with those of a square. Perimeter of a kite with sides a and b is given by $2\left[a+b\right]$.. Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1.
From www.geogebra.org
LR703XT3 (Diagonals of a kite) GeoGebra Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1 In a kite, the diagonals are perpendicular bisectors of each other, with one diagonal being the angle bisector of the opposite angles. Properties of a kite perpendicular diagonals the diagonals of a kite are perpendicular to each other. The area of kite $= \frac{1}{2} \times d_1 \times d_2$, where $d_1,\; D_2$ are lengths of diagonals. Solution for compare the properties. Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1.
From www.slideshare.net
Quadrilateral Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1 Perimeter of a kite with sides a and b is given by $2\left[a+b\right]$. D_2$ are lengths of diagonals. Solution for compare the properties of the diagonals of a kite with those of a square In a kite, the diagonals are perpendicular bisectors of each other, with one diagonal being the angle bisector of the opposite angles. The area of kite. Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1.
From lessonmagicisidro.z21.web.core.windows.net
All The Properties Of A Square Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1 Perimeter of a kite with sides a and b is given by $2\left[a+b\right]$. Study with quizlet and memorize flashcards containing terms like what do the diagonals have to do with each other?, why are there right. D_2$ are lengths of diagonals. We have the right solution; In a kite, the diagonals are perpendicular bisectors of each other, with one diagonal. Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1.
From misscalculate.blogspot.com
misscalcul8 Properties of Diagonals Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1 Perimeter of a kite with sides a and b is given by $2\left[a+b\right]$. Compare the properties of the diagonals of a kite with those of a square. Solution for compare the properties of the diagonals of a kite with those of a square D_2$ are lengths of diagonals. Study with quizlet and memorize flashcards containing terms like what do the. Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1.
From animalia-life.club
Square Area Formula Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1 Compare the properties of the diagonals of a kite with those of a square. Properties of a kite perpendicular diagonals the diagonals of a kite are perpendicular to each other. The area of kite $= \frac{1}{2} \times d_1 \times d_2$, where $d_1,\; Study with quizlet and memorize flashcards containing terms like what do the diagonals have to do with each. Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1.
From www.gauthmath.com
Solved The diagram below shows a kite ABCD. The diagonals cut at right Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1 Properties of a kite perpendicular diagonals the diagonals of a kite are perpendicular to each other. The area of kite $= \frac{1}{2} \times d_1 \times d_2$, where $d_1,\; We have the right solution; Perimeter of a kite with sides a and b is given by $2\left[a+b\right]$. D_2$ are lengths of diagonals. Solution for compare the properties of the diagonals of. Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1.
From www.geeksforgeeks.org
Program to calculate the area of Kite Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1 Compare the properties of the diagonals of a kite with those of a square. Solution for compare the properties of the diagonals of a kite with those of a square The area of kite $= \frac{1}{2} \times d_1 \times d_2$, where $d_1,\; We have the right solution; Properties of a kite perpendicular diagonals the diagonals of a kite are perpendicular. Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1.
From www.cuemath.com
Area of a Kite Formula, Definition, Examples Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1 We have the right solution; Properties of a kite perpendicular diagonals the diagonals of a kite are perpendicular to each other. Study with quizlet and memorize flashcards containing terms like what do the diagonals have to do with each other?, why are there right. The area of kite $= \frac{1}{2} \times d_1 \times d_2$, where $d_1,\; Perimeter of a kite. Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1.
From www.youtube.com
Prove Diagonals of a Kite are Perpendicular YouTube Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1 The area of kite $= \frac{1}{2} \times d_1 \times d_2$, where $d_1,\; In a kite, the diagonals are perpendicular bisectors of each other, with one diagonal being the angle bisector of the opposite angles. Compare the properties of the diagonals of a kite with those of a square. Perimeter of a kite with sides a and b is given by. Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1.
From www.slideserve.com
PPT Geometry 66 Kites PowerPoint Presentation ID2721679 Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1 Solution for compare the properties of the diagonals of a kite with those of a square Compare the properties of the diagonals of a kite with those of a square. The area of kite $= \frac{1}{2} \times d_1 \times d_2$, where $d_1,\; In a kite, the diagonals are perpendicular bisectors of each other, with one diagonal being the angle bisector. Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1.
From www.splashlearn.com
Properties of a Kite Definition, Diagonals, Examples, Facts Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1 Perimeter of a kite with sides a and b is given by $2\left[a+b\right]$. Compare the properties of the diagonals of a kite with those of a square. In a kite, the diagonals are perpendicular bisectors of each other, with one diagonal being the angle bisector of the opposite angles. We have the right solution; Properties of a kite perpendicular diagonals. Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1.
From ar.inspiredpencil.com
Congruent Diagonals Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1 The area of kite $= \frac{1}{2} \times d_1 \times d_2$, where $d_1,\; In a kite, the diagonals are perpendicular bisectors of each other, with one diagonal being the angle bisector of the opposite angles. Properties of a kite perpendicular diagonals the diagonals of a kite are perpendicular to each other. Perimeter of a kite with sides a and b is. Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1.
From ar.inspiredpencil.com
Kite Definition Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1 The area of kite $= \frac{1}{2} \times d_1 \times d_2$, where $d_1,\; Solution for compare the properties of the diagonals of a kite with those of a square In a kite, the diagonals are perpendicular bisectors of each other, with one diagonal being the angle bisector of the opposite angles. We have the right solution; Study with quizlet and memorize. Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1.
From quizzmagicbelford.z21.web.core.windows.net
Properties Of A Kite Shape Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1 In a kite, the diagonals are perpendicular bisectors of each other, with one diagonal being the angle bisector of the opposite angles. Perimeter of a kite with sides a and b is given by $2\left[a+b\right]$. Study with quizlet and memorize flashcards containing terms like what do the diagonals have to do with each other?, why are there right. Solution for. Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1.
From www.toppr.com
In the given figure, AC and BC are the diagonals of Kite ABCD with AB Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1 Study with quizlet and memorize flashcards containing terms like what do the diagonals have to do with each other?, why are there right. The area of kite $= \frac{1}{2} \times d_1 \times d_2$, where $d_1,\; Compare the properties of the diagonals of a kite with those of a square. Solution for compare the properties of the diagonals of a kite. Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1.
From www.toppr.com
Properties of Parallelogram, Rhombus, Rectangle and Square Examples Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1 Perimeter of a kite with sides a and b is given by $2\left[a+b\right]$. Solution for compare the properties of the diagonals of a kite with those of a square Study with quizlet and memorize flashcards containing terms like what do the diagonals have to do with each other?, why are there right. Properties of a kite perpendicular diagonals the diagonals. Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1.
From www.geeksforgeeks.org
Quadrilateral Definition, Properties, Types, Formulas, Examples Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1 Perimeter of a kite with sides a and b is given by $2\left[a+b\right]$. We have the right solution; D_2$ are lengths of diagonals. Study with quizlet and memorize flashcards containing terms like what do the diagonals have to do with each other?, why are there right. The area of kite $= \frac{1}{2} \times d_1 \times d_2$, where $d_1,\; Compare the. Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1.
From www.cuemath.com
Properties of kite Definition of Kite with Solved Examples Cuemath Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1 The area of kite $= \frac{1}{2} \times d_1 \times d_2$, where $d_1,\; Compare the properties of the diagonals of a kite with those of a square. Solution for compare the properties of the diagonals of a kite with those of a square In a kite, the diagonals are perpendicular bisectors of each other, with one diagonal being the angle bisector. Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1.
From exoswmvur.blob.core.windows.net
Compare The Properties Of The Diagonals Of A Kite With Those Of A Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1 Study with quizlet and memorize flashcards containing terms like what do the diagonals have to do with each other?, why are there right. In a kite, the diagonals are perpendicular bisectors of each other, with one diagonal being the angle bisector of the opposite angles. Perimeter of a kite with sides a and b is given by $2\left[a+b\right]$. The area. Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1.
From byjus.com
20. Show that the diagonals of a square are equal and bisect each other Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1 Compare the properties of the diagonals of a kite with those of a square. The area of kite $= \frac{1}{2} \times d_1 \times d_2$, where $d_1,\; We have the right solution; Perimeter of a kite with sides a and b is given by $2\left[a+b\right]$. Properties of a kite perpendicular diagonals the diagonals of a kite are perpendicular to each other.. Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1.
From byjus.com
In which of the following quadrilaterals are the diagonals Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1 We have the right solution; Study with quizlet and memorize flashcards containing terms like what do the diagonals have to do with each other?, why are there right. Perimeter of a kite with sides a and b is given by $2\left[a+b\right]$. Solution for compare the properties of the diagonals of a kite with those of a square Properties of a. Compare The Properties Of The Diagonals Of A Kite With Those Of A Square Site 1.