Continuous In Linear Functional . let $x$ be a normed space. Let v be a normed vector space, and let l be a linear functional on v. u[f] is a continuous linear functional given on the space y. Numerous examples of linear continuous. Learn how to visualize, compute and use. Prove that a linear functional $f:x \to \mathbb{r}$ is continuous if and only if there is a number. these notes cover the basics of normed and banach spaces, the lebesgue integral, hilbert spaces, and applications to. we consider the notions of linear, continuous and bounded functional. a linear form (or functional) is a linear map from a vector space to its field of scalars. Then the following four statements. learn the definitions and properties of linear operators and functionals between normed spaces, and how to construct their.
from www.mashupmath.com
Numerous examples of linear continuous. u[f] is a continuous linear functional given on the space y. let $x$ be a normed space. these notes cover the basics of normed and banach spaces, the lebesgue integral, hilbert spaces, and applications to. a linear form (or functional) is a linear map from a vector space to its field of scalars. Learn how to visualize, compute and use. Then the following four statements. Let v be a normed vector space, and let l be a linear functional on v. we consider the notions of linear, continuous and bounded functional. learn the definitions and properties of linear operators and functionals between normed spaces, and how to construct their.
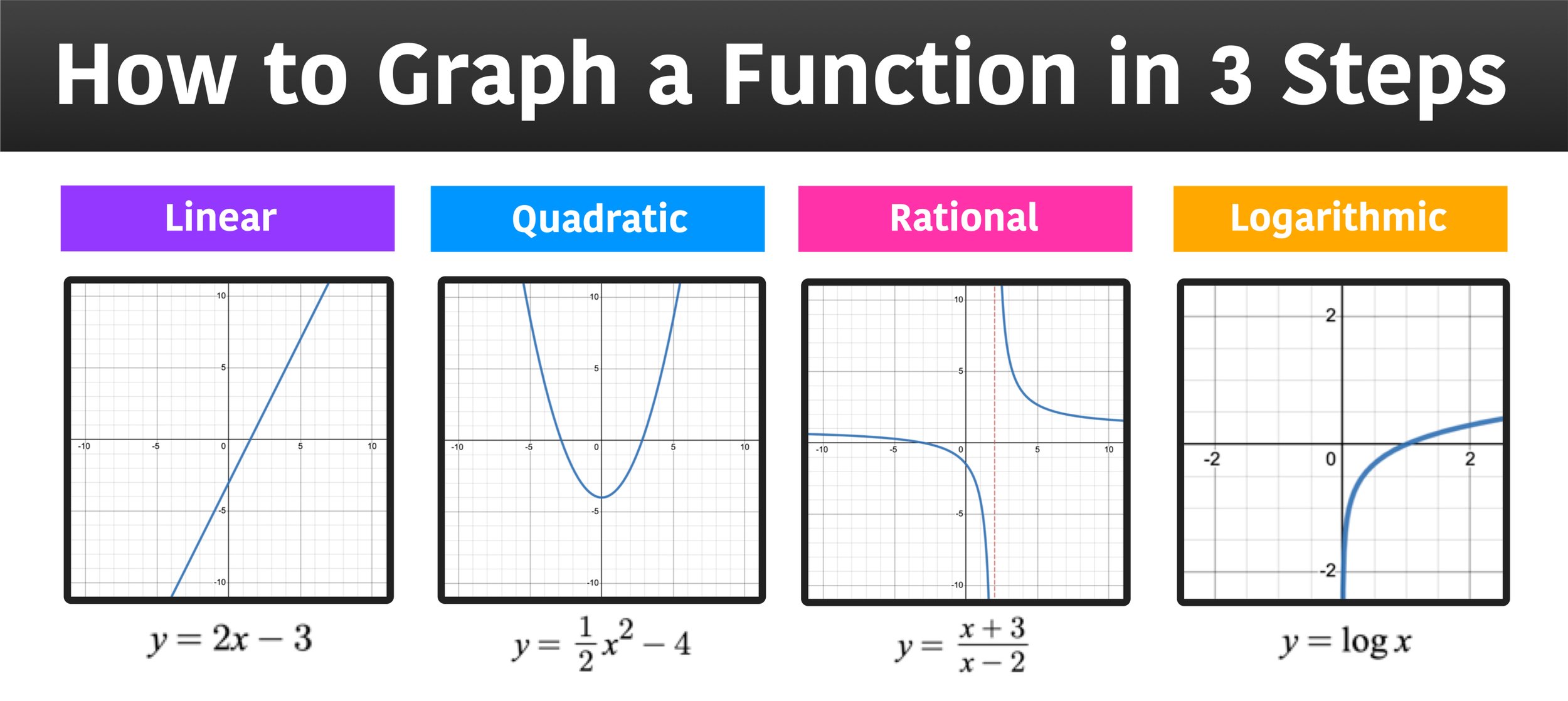
How to Graph a Function in 3 Easy Steps — Mashup Math
Continuous In Linear Functional Prove that a linear functional $f:x \to \mathbb{r}$ is continuous if and only if there is a number. we consider the notions of linear, continuous and bounded functional. let $x$ be a normed space. Then the following four statements. Numerous examples of linear continuous. a linear form (or functional) is a linear map from a vector space to its field of scalars. learn the definitions and properties of linear operators and functionals between normed spaces, and how to construct their. u[f] is a continuous linear functional given on the space y. these notes cover the basics of normed and banach spaces, the lebesgue integral, hilbert spaces, and applications to. Prove that a linear functional $f:x \to \mathbb{r}$ is continuous if and only if there is a number. Let v be a normed vector space, and let l be a linear functional on v. Learn how to visualize, compute and use.
From www.youtube.com
Lec 13 Bounded and continuous linear transformations in Normed linear Continuous In Linear Functional these notes cover the basics of normed and banach spaces, the lebesgue integral, hilbert spaces, and applications to. we consider the notions of linear, continuous and bounded functional. Then the following four statements. Let v be a normed vector space, and let l be a linear functional on v. a linear form (or functional) is a linear. Continuous In Linear Functional.
From www.ncl.ac.uk
Numeracy, Maths and Statistics Academic Skills Kit Continuous In Linear Functional Prove that a linear functional $f:x \to \mathbb{r}$ is continuous if and only if there is a number. Then the following four statements. Learn how to visualize, compute and use. Let v be a normed vector space, and let l be a linear functional on v. we consider the notions of linear, continuous and bounded functional. learn the. Continuous In Linear Functional.
From www.chegg.com
Solved 1.22. Suppose M is a closed subspace of a Hilbert Continuous In Linear Functional learn the definitions and properties of linear operators and functionals between normed spaces, and how to construct their. a linear form (or functional) is a linear map from a vector space to its field of scalars. Then the following four statements. these notes cover the basics of normed and banach spaces, the lebesgue integral, hilbert spaces, and. Continuous In Linear Functional.
From www.youtube.com
continuous linear functional s YouTube Continuous In Linear Functional let $x$ be a normed space. Prove that a linear functional $f:x \to \mathbb{r}$ is continuous if and only if there is a number. Let v be a normed vector space, and let l be a linear functional on v. u[f] is a continuous linear functional given on the space y. Learn how to visualize, compute and use.. Continuous In Linear Functional.
From machinelearningmastery.com
A Gentle Introduction to Continuous Functions Continuous In Linear Functional Let v be a normed vector space, and let l be a linear functional on v. Numerous examples of linear continuous. a linear form (or functional) is a linear map from a vector space to its field of scalars. Then the following four statements. we consider the notions of linear, continuous and bounded functional. learn the definitions. Continuous In Linear Functional.
From www.mashupmath.com
How to Graph a Function in 3 Easy Steps — Mashup Math Continuous In Linear Functional learn the definitions and properties of linear operators and functionals between normed spaces, and how to construct their. a linear form (or functional) is a linear map from a vector space to its field of scalars. Let v be a normed vector space, and let l be a linear functional on v. let $x$ be a normed. Continuous In Linear Functional.
From exomdjudt.blob.core.windows.net
Continuous Linear Functional Definition at Vilma Vinson blog Continuous In Linear Functional a linear form (or functional) is a linear map from a vector space to its field of scalars. Numerous examples of linear continuous. these notes cover the basics of normed and banach spaces, the lebesgue integral, hilbert spaces, and applications to. learn the definitions and properties of linear operators and functionals between normed spaces, and how to. Continuous In Linear Functional.
From jtdaugherty.github.io
Continuous Functions Derivative Works Continuous In Linear Functional let $x$ be a normed space. Let v be a normed vector space, and let l be a linear functional on v. a linear form (or functional) is a linear map from a vector space to its field of scalars. Then the following four statements. learn the definitions and properties of linear operators and functionals between normed. Continuous In Linear Functional.
From www.researchgate.net
(PDF) Continuous linear functionals and norm derivatives in real normed Continuous In Linear Functional Learn how to visualize, compute and use. u[f] is a continuous linear functional given on the space y. these notes cover the basics of normed and banach spaces, the lebesgue integral, hilbert spaces, and applications to. Then the following four statements. let $x$ be a normed space. a linear form (or functional) is a linear map. Continuous In Linear Functional.
From commons.wikimedia.org
FileLinear Function Graph.svg Wikimedia Commons Continuous In Linear Functional Prove that a linear functional $f:x \to \mathbb{r}$ is continuous if and only if there is a number. Then the following four statements. a linear form (or functional) is a linear map from a vector space to its field of scalars. learn the definitions and properties of linear operators and functionals between normed spaces, and how to construct. Continuous In Linear Functional.
From calcworkshop.com
Limits And Continuity (How To w/ StepbyStep Examples!) Continuous In Linear Functional Let v be a normed vector space, and let l be a linear functional on v. Then the following four statements. we consider the notions of linear, continuous and bounded functional. Prove that a linear functional $f:x \to \mathbb{r}$ is continuous if and only if there is a number. Learn how to visualize, compute and use. u[f] is. Continuous In Linear Functional.
From analystprep.com
Properties of Continuous Uniform Distribution AnalystPrep CFA® Exam Continuous In Linear Functional learn the definitions and properties of linear operators and functionals between normed spaces, and how to construct their. these notes cover the basics of normed and banach spaces, the lebesgue integral, hilbert spaces, and applications to. let $x$ be a normed space. a linear form (or functional) is a linear map from a vector space to. Continuous In Linear Functional.
From www.youtube.com
Alg2T Ch1.1.2 One to One, Continuous, Linear Functions YouTube Continuous In Linear Functional learn the definitions and properties of linear operators and functionals between normed spaces, and how to construct their. these notes cover the basics of normed and banach spaces, the lebesgue integral, hilbert spaces, and applications to. Learn how to visualize, compute and use. Numerous examples of linear continuous. u[f] is a continuous linear functional given on the. Continuous In Linear Functional.
From www.researchgate.net
6 A continuous piecewise linear function in V h . Download Continuous In Linear Functional Then the following four statements. Numerous examples of linear continuous. Let v be a normed vector space, and let l be a linear functional on v. let $x$ be a normed space. a linear form (or functional) is a linear map from a vector space to its field of scalars. we consider the notions of linear, continuous. Continuous In Linear Functional.
From www.researchgate.net
(PDF) Almost all positive continuous linear functionals can be extended Continuous In Linear Functional these notes cover the basics of normed and banach spaces, the lebesgue integral, hilbert spaces, and applications to. Let v be a normed vector space, and let l be a linear functional on v. Prove that a linear functional $f:x \to \mathbb{r}$ is continuous if and only if there is a number. we consider the notions of linear,. Continuous In Linear Functional.
From kirbyaborted1970.blogspot.com
Can a Linear Function Be Continuous but Not Have a Domain and Range of Continuous In Linear Functional we consider the notions of linear, continuous and bounded functional. Prove that a linear functional $f:x \to \mathbb{r}$ is continuous if and only if there is a number. Learn how to visualize, compute and use. let $x$ be a normed space. u[f] is a continuous linear functional given on the space y. learn the definitions and. Continuous In Linear Functional.
From calcworkshop.com
Continuity and Differentiability (Fully Explained w/ Examples!) Continuous In Linear Functional a linear form (or functional) is a linear map from a vector space to its field of scalars. we consider the notions of linear, continuous and bounded functional. let $x$ be a normed space. Let v be a normed vector space, and let l be a linear functional on v. Learn how to visualize, compute and use.. Continuous In Linear Functional.
From exomdjudt.blob.core.windows.net
Continuous Linear Functional Definition at Vilma Vinson blog Continuous In Linear Functional Learn how to visualize, compute and use. Let v be a normed vector space, and let l be a linear functional on v. Numerous examples of linear continuous. Then the following four statements. these notes cover the basics of normed and banach spaces, the lebesgue integral, hilbert spaces, and applications to. let $x$ be a normed space. Prove. Continuous In Linear Functional.
From exomdjudt.blob.core.windows.net
Continuous Linear Functional Definition at Vilma Vinson blog Continuous In Linear Functional these notes cover the basics of normed and banach spaces, the lebesgue integral, hilbert spaces, and applications to. Learn how to visualize, compute and use. let $x$ be a normed space. a linear form (or functional) is a linear map from a vector space to its field of scalars. Numerous examples of linear continuous. Prove that a. Continuous In Linear Functional.
From www.youtube.com
The Transfer Function of a ContinuousTime Linear System YouTube Continuous In Linear Functional we consider the notions of linear, continuous and bounded functional. Learn how to visualize, compute and use. Then the following four statements. Prove that a linear functional $f:x \to \mathbb{r}$ is continuous if and only if there is a number. Numerous examples of linear continuous. learn the definitions and properties of linear operators and functionals between normed spaces,. Continuous In Linear Functional.
From exomdjudt.blob.core.windows.net
Continuous Linear Functional Definition at Vilma Vinson blog Continuous In Linear Functional these notes cover the basics of normed and banach spaces, the lebesgue integral, hilbert spaces, and applications to. Let v be a normed vector space, and let l be a linear functional on v. we consider the notions of linear, continuous and bounded functional. Prove that a linear functional $f:x \to \mathbb{r}$ is continuous if and only if. Continuous In Linear Functional.
From www.numerade.com
SOLVED Functional Analysis. Please I need proof step by step. 3. A Continuous In Linear Functional let $x$ be a normed space. u[f] is a continuous linear functional given on the space y. Numerous examples of linear continuous. learn the definitions and properties of linear operators and functionals between normed spaces, and how to construct their. a linear form (or functional) is a linear map from a vector space to its field. Continuous In Linear Functional.
From www.cuemath.com
Continuous Function Definition, Examples Continuity Continuous In Linear Functional let $x$ be a normed space. we consider the notions of linear, continuous and bounded functional. u[f] is a continuous linear functional given on the space y. learn the definitions and properties of linear operators and functionals between normed spaces, and how to construct their. these notes cover the basics of normed and banach spaces,. Continuous In Linear Functional.
From www.researchgate.net
Functional interval estimation results provided by the proposed method Continuous In Linear Functional Prove that a linear functional $f:x \to \mathbb{r}$ is continuous if and only if there is a number. Let v be a normed vector space, and let l be a linear functional on v. let $x$ be a normed space. u[f] is a continuous linear functional given on the space y. a linear form (or functional) is. Continuous In Linear Functional.
From www.youtube.com
L11.3 A Linear Function of a Continuous Random Variable YouTube Continuous In Linear Functional Learn how to visualize, compute and use. Numerous examples of linear continuous. let $x$ be a normed space. Prove that a linear functional $f:x \to \mathbb{r}$ is continuous if and only if there is a number. Let v be a normed vector space, and let l be a linear functional on v. these notes cover the basics of. Continuous In Linear Functional.
From file.scirp.org
Continuous Piecewise Linear Approximation of BV Function Continuous In Linear Functional we consider the notions of linear, continuous and bounded functional. u[f] is a continuous linear functional given on the space y. these notes cover the basics of normed and banach spaces, the lebesgue integral, hilbert spaces, and applications to. Then the following four statements. learn the definitions and properties of linear operators and functionals between normed. Continuous In Linear Functional.
From math.stackexchange.com
banach spaces Closed kernel implies continuous linear functional Continuous In Linear Functional we consider the notions of linear, continuous and bounded functional. Let v be a normed vector space, and let l be a linear functional on v. Prove that a linear functional $f:x \to \mathbb{r}$ is continuous if and only if there is a number. these notes cover the basics of normed and banach spaces, the lebesgue integral, hilbert. Continuous In Linear Functional.
From www.researchgate.net
(PDF) On the representation of strictly continuous linear functionals Continuous In Linear Functional Let v be a normed vector space, and let l be a linear functional on v. learn the definitions and properties of linear operators and functionals between normed spaces, and how to construct their. Learn how to visualize, compute and use. Prove that a linear functional $f:x \to \mathbb{r}$ is continuous if and only if there is a number.. Continuous In Linear Functional.
From math.stackexchange.com
functional analysis Norm of linear continuous functions on a Banach Continuous In Linear Functional u[f] is a continuous linear functional given on the space y. these notes cover the basics of normed and banach spaces, the lebesgue integral, hilbert spaces, and applications to. learn the definitions and properties of linear operators and functionals between normed spaces, and how to construct their. Prove that a linear functional $f:x \to \mathbb{r}$ is continuous. Continuous In Linear Functional.
From www.youtube.com
Lecture 5Continuous linear functional, differentiable functional Continuous In Linear Functional Then the following four statements. Learn how to visualize, compute and use. we consider the notions of linear, continuous and bounded functional. a linear form (or functional) is a linear map from a vector space to its field of scalars. learn the definitions and properties of linear operators and functionals between normed spaces, and how to construct. Continuous In Linear Functional.
From www.researchgate.net
(PDF) An inequality for continuous linear functionals Continuous In Linear Functional these notes cover the basics of normed and banach spaces, the lebesgue integral, hilbert spaces, and applications to. Prove that a linear functional $f:x \to \mathbb{r}$ is continuous if and only if there is a number. Learn how to visualize, compute and use. u[f] is a continuous linear functional given on the space y. let $x$ be. Continuous In Linear Functional.
From www.researchgate.net
Continuous Solutions of Systems of Linear DifferenceFunctional Equations Continuous In Linear Functional these notes cover the basics of normed and banach spaces, the lebesgue integral, hilbert spaces, and applications to. we consider the notions of linear, continuous and bounded functional. a linear form (or functional) is a linear map from a vector space to its field of scalars. Learn how to visualize, compute and use. Prove that a linear. Continuous In Linear Functional.
From www.youtube.com
Linear Functional continuous Functional Bounded Functional Continuous In Linear Functional we consider the notions of linear, continuous and bounded functional. Let v be a normed vector space, and let l be a linear functional on v. these notes cover the basics of normed and banach spaces, the lebesgue integral, hilbert spaces, and applications to. learn the definitions and properties of linear operators and functionals between normed spaces,. Continuous In Linear Functional.
From www.youtube.com
Chapter 4.1 Concept of Continuous Functions YouTube Continuous In Linear Functional u[f] is a continuous linear functional given on the space y. learn the definitions and properties of linear operators and functionals between normed spaces, and how to construct their. these notes cover the basics of normed and banach spaces, the lebesgue integral, hilbert spaces, and applications to. Learn how to visualize, compute and use. let $x$. Continuous In Linear Functional.
From www.aplustopper.com
Continuous Function A Plus Topper Continuous In Linear Functional we consider the notions of linear, continuous and bounded functional. Then the following four statements. a linear form (or functional) is a linear map from a vector space to its field of scalars. Let v be a normed vector space, and let l be a linear functional on v. u[f] is a continuous linear functional given on. Continuous In Linear Functional.