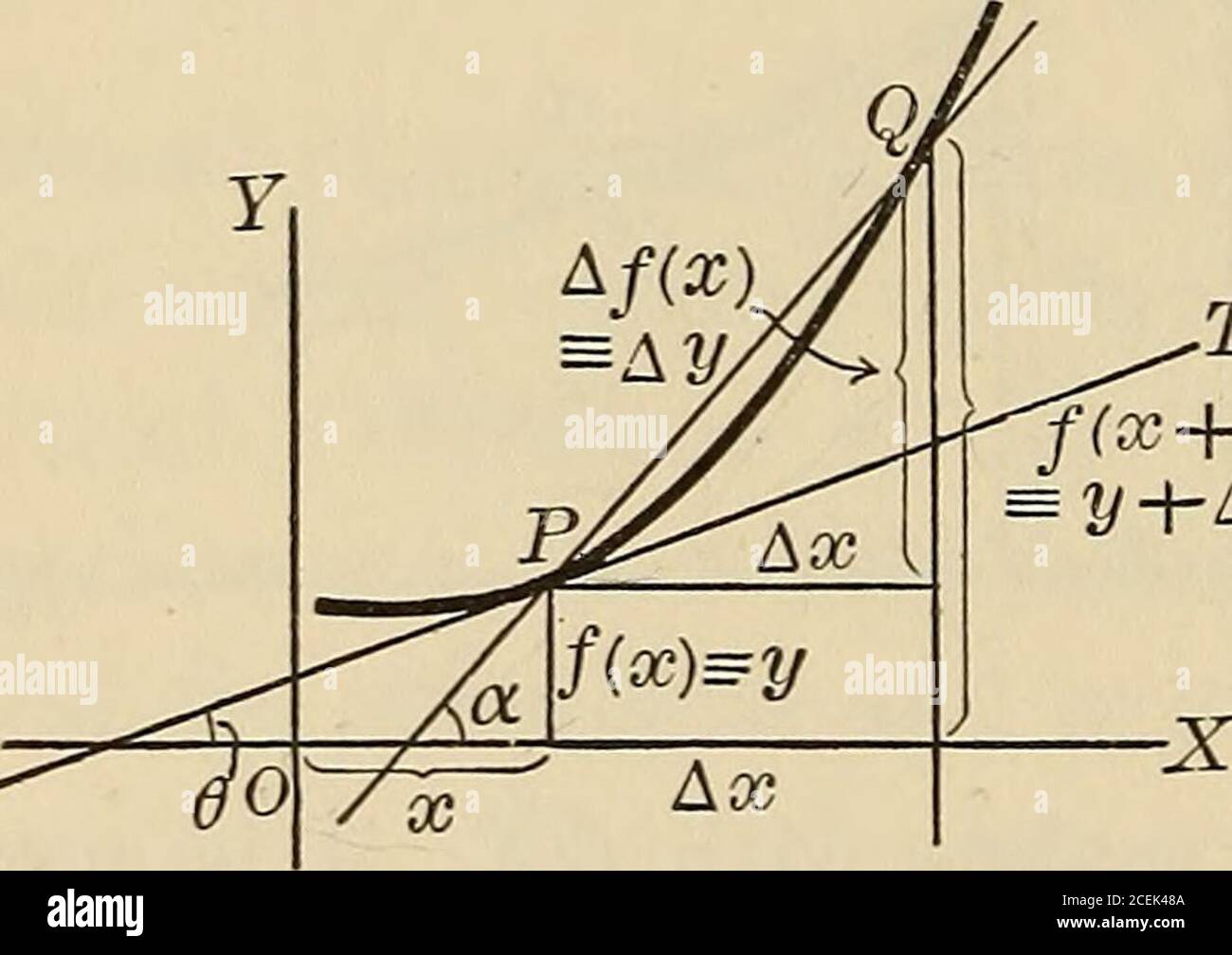
Differentials Explained Calculus . Differential calculus is a branch of calculus involving the study of derivatives that are used to find the instantaneous rate of change of a function using the process of differentiation. When we first looked at derivatives, we used the. Differentials provide us with a way of estimating the amount a function changes as a result of a small change in input values. There is a natural extension to functions of three or more variables. In section 2.2 we explored the meaning and use of the derivative. Finding the slope of a tangent line to a curve (the derivative). For instance, given the function w = g(x,y,z) w = g (x, y, z) the. Given a function \(y = f\left( x \right)\) we call \(dy\) and \(dx\) differentials and the relationship between them is given by, \[dy. Recall that the derivative of a. This section starts by revisiting some of those ideas.
from www.alamy.com
There is a natural extension to functions of three or more variables. Differential calculus is a branch of calculus involving the study of derivatives that are used to find the instantaneous rate of change of a function using the process of differentiation. Recall that the derivative of a. In section 2.2 we explored the meaning and use of the derivative. For instance, given the function w = g(x,y,z) w = g (x, y, z) the. This section starts by revisiting some of those ideas. Differentials provide us with a way of estimating the amount a function changes as a result of a small change in input values. When we first looked at derivatives, we used the. Given a function \(y = f\left( x \right)\) we call \(dy\) and \(dx\) differentials and the relationship between them is given by, \[dy. Finding the slope of a tangent line to a curve (the derivative).
. Differential and integral calculus, an introductory course for
Differentials Explained Calculus Differentials provide us with a way of estimating the amount a function changes as a result of a small change in input values. Differential calculus is a branch of calculus involving the study of derivatives that are used to find the instantaneous rate of change of a function using the process of differentiation. Differentials provide us with a way of estimating the amount a function changes as a result of a small change in input values. There is a natural extension to functions of three or more variables. Given a function \(y = f\left( x \right)\) we call \(dy\) and \(dx\) differentials and the relationship between them is given by, \[dy. Recall that the derivative of a. When we first looked at derivatives, we used the. This section starts by revisiting some of those ideas. Finding the slope of a tangent line to a curve (the derivative). In section 2.2 we explored the meaning and use of the derivative. For instance, given the function w = g(x,y,z) w = g (x, y, z) the.
From www.wjscience.us
Differential calculus formulas Differentials Explained Calculus Recall that the derivative of a. Differential calculus is a branch of calculus involving the study of derivatives that are used to find the instantaneous rate of change of a function using the process of differentiation. Finding the slope of a tangent line to a curve (the derivative). In section 2.2 we explored the meaning and use of the derivative.. Differentials Explained Calculus.
From www.youtube.com
Differentials and linearization in Multivariable Calculus YouTube Differentials Explained Calculus For instance, given the function w = g(x,y,z) w = g (x, y, z) the. Finding the slope of a tangent line to a curve (the derivative). Recall that the derivative of a. Differential calculus is a branch of calculus involving the study of derivatives that are used to find the instantaneous rate of change of a function using the. Differentials Explained Calculus.
From www.youtube.com
Differential Calculus Explained in Just 4 Minutes YouTube Differentials Explained Calculus Differentials provide us with a way of estimating the amount a function changes as a result of a small change in input values. In section 2.2 we explored the meaning and use of the derivative. Differential calculus is a branch of calculus involving the study of derivatives that are used to find the instantaneous rate of change of a function. Differentials Explained Calculus.
From exoznzrdk.blob.core.windows.net
Differential Calculus Explained at Casey Messenger blog Differentials Explained Calculus For instance, given the function w = g(x,y,z) w = g (x, y, z) the. Recall that the derivative of a. Given a function \(y = f\left( x \right)\) we call \(dy\) and \(dx\) differentials and the relationship between them is given by, \[dy. Finding the slope of a tangent line to a curve (the derivative). There is a natural. Differentials Explained Calculus.
From www.youtube.com
Learn differential calculus in 10 minutes YouTube Differentials Explained Calculus Finding the slope of a tangent line to a curve (the derivative). When we first looked at derivatives, we used the. For instance, given the function w = g(x,y,z) w = g (x, y, z) the. Given a function \(y = f\left( x \right)\) we call \(dy\) and \(dx\) differentials and the relationship between them is given by, \[dy. Differentials. Differentials Explained Calculus.
From unacademy.com
CA Foundation Differential Calculus IV Use Code SS12 Concepts Differentials Explained Calculus Finding the slope of a tangent line to a curve (the derivative). In section 2.2 we explored the meaning and use of the derivative. For instance, given the function w = g(x,y,z) w = g (x, y, z) the. This section starts by revisiting some of those ideas. There is a natural extension to functions of three or more variables.. Differentials Explained Calculus.
From www.youtube.com
Infinite Limits Differential Calculus Explained in Filipino YouTube Differentials Explained Calculus Differential calculus is a branch of calculus involving the study of derivatives that are used to find the instantaneous rate of change of a function using the process of differentiation. When we first looked at derivatives, we used the. There is a natural extension to functions of three or more variables. Recall that the derivative of a. For instance, given. Differentials Explained Calculus.
From www.studypool.com
SOLUTION Differential and integral calculus by feliciano and uy Differentials Explained Calculus For instance, given the function w = g(x,y,z) w = g (x, y, z) the. There is a natural extension to functions of three or more variables. Recall that the derivative of a. This section starts by revisiting some of those ideas. Differential calculus is a branch of calculus involving the study of derivatives that are used to find the. Differentials Explained Calculus.
From www.youtube.com
Differential Calculus Gradient First Principle Limit Explained YouTube Differentials Explained Calculus Given a function \(y = f\left( x \right)\) we call \(dy\) and \(dx\) differentials and the relationship between them is given by, \[dy. There is a natural extension to functions of three or more variables. Differential calculus is a branch of calculus involving the study of derivatives that are used to find the instantaneous rate of change of a function. Differentials Explained Calculus.
From exoznzrdk.blob.core.windows.net
Differential Calculus Explained at Casey Messenger blog Differentials Explained Calculus For instance, given the function w = g(x,y,z) w = g (x, y, z) the. There is a natural extension to functions of three or more variables. Finding the slope of a tangent line to a curve (the derivative). When we first looked at derivatives, we used the. This section starts by revisiting some of those ideas. Given a function. Differentials Explained Calculus.
From www.scribd.com
Partial Derivatives, Jacobians, Differentials, and Other Calculus Differentials Explained Calculus Given a function \(y = f\left( x \right)\) we call \(dy\) and \(dx\) differentials and the relationship between them is given by, \[dy. In section 2.2 we explored the meaning and use of the derivative. When we first looked at derivatives, we used the. There is a natural extension to functions of three or more variables. For instance, given the. Differentials Explained Calculus.
From www.alamy.com
. Differential and integral calculus, an introductory course for Differentials Explained Calculus For instance, given the function w = g(x,y,z) w = g (x, y, z) the. In section 2.2 we explored the meaning and use of the derivative. Recall that the derivative of a. This section starts by revisiting some of those ideas. There is a natural extension to functions of three or more variables. Given a function \(y = f\left(. Differentials Explained Calculus.
From www.studypool.com
SOLUTION Math Differential calculus problem solving and solutions Differentials Explained Calculus Differentials provide us with a way of estimating the amount a function changes as a result of a small change in input values. Finding the slope of a tangent line to a curve (the derivative). Recall that the derivative of a. There is a natural extension to functions of three or more variables. For instance, given the function w =. Differentials Explained Calculus.
From www.studocu.com
Differential and Integral Calculus Formula Mechanical Engineering Differentials Explained Calculus Recall that the derivative of a. In section 2.2 we explored the meaning and use of the derivative. When we first looked at derivatives, we used the. Differentials provide us with a way of estimating the amount a function changes as a result of a small change in input values. Differential calculus is a branch of calculus involving the study. Differentials Explained Calculus.
From www.reddit.com
Product of differentials r/calculus Differentials Explained Calculus Differentials provide us with a way of estimating the amount a function changes as a result of a small change in input values. In section 2.2 we explored the meaning and use of the derivative. Recall that the derivative of a. This section starts by revisiting some of those ideas. Given a function \(y = f\left( x \right)\) we call. Differentials Explained Calculus.
From www.youtube.com
Differential Equations in Calculus 1 YouTube Differentials Explained Calculus For instance, given the function w = g(x,y,z) w = g (x, y, z) the. When we first looked at derivatives, we used the. This section starts by revisiting some of those ideas. Differential calculus is a branch of calculus involving the study of derivatives that are used to find the instantaneous rate of change of a function using the. Differentials Explained Calculus.
From www.studypool.com
SOLUTION Calculus CH14.6 tangent planes and differentials Studypool Differentials Explained Calculus Finding the slope of a tangent line to a curve (the derivative). When we first looked at derivatives, we used the. Recall that the derivative of a. For instance, given the function w = g(x,y,z) w = g (x, y, z) the. Given a function \(y = f\left( x \right)\) we call \(dy\) and \(dx\) differentials and the relationship between. Differentials Explained Calculus.
From studylibrarygodward.z13.web.core.windows.net
Chain Rule Derivative Explained Differentials Explained Calculus Differential calculus is a branch of calculus involving the study of derivatives that are used to find the instantaneous rate of change of a function using the process of differentiation. Differentials provide us with a way of estimating the amount a function changes as a result of a small change in input values. Recall that the derivative of a. Given. Differentials Explained Calculus.
From www.shiksha.com
Differential Calculus for Data Science Shiksha Online Differentials Explained Calculus There is a natural extension to functions of three or more variables. For instance, given the function w = g(x,y,z) w = g (x, y, z) the. Given a function \(y = f\left( x \right)\) we call \(dy\) and \(dx\) differentials and the relationship between them is given by, \[dy. Differential calculus is a branch of calculus involving the study. Differentials Explained Calculus.
From www.youtube.com
Calculus I Differential Equations YouTube Differentials Explained Calculus There is a natural extension to functions of three or more variables. Differentials provide us with a way of estimating the amount a function changes as a result of a small change in input values. For instance, given the function w = g(x,y,z) w = g (x, y, z) the. Given a function \(y = f\left( x \right)\) we call. Differentials Explained Calculus.
From exoznzrdk.blob.core.windows.net
Differential Calculus Explained at Casey Messenger blog Differentials Explained Calculus In section 2.2 we explored the meaning and use of the derivative. When we first looked at derivatives, we used the. Given a function \(y = f\left( x \right)\) we call \(dy\) and \(dx\) differentials and the relationship between them is given by, \[dy. There is a natural extension to functions of three or more variables. Finding the slope of. Differentials Explained Calculus.
From www.tes.com
Calculus Differentiation Teaching Resources Differentials Explained Calculus When we first looked at derivatives, we used the. Recall that the derivative of a. Differential calculus is a branch of calculus involving the study of derivatives that are used to find the instantaneous rate of change of a function using the process of differentiation. There is a natural extension to functions of three or more variables. Differentials provide us. Differentials Explained Calculus.
From www.teacharesources.com
Differential Calculus • Teacha! Differentials Explained Calculus This section starts by revisiting some of those ideas. Finding the slope of a tangent line to a curve (the derivative). Differential calculus is a branch of calculus involving the study of derivatives that are used to find the instantaneous rate of change of a function using the process of differentiation. In section 2.2 we explored the meaning and use. Differentials Explained Calculus.
From byjus.com
Differential Calculus (Formulas and Examples) Differentials Explained Calculus When we first looked at derivatives, we used the. Recall that the derivative of a. Differential calculus is a branch of calculus involving the study of derivatives that are used to find the instantaneous rate of change of a function using the process of differentiation. There is a natural extension to functions of three or more variables. Finding the slope. Differentials Explained Calculus.
From www.scribd.com
Explain Product Rule PDF Differential Calculus Function (Mathematics) Differentials Explained Calculus Given a function \(y = f\left( x \right)\) we call \(dy\) and \(dx\) differentials and the relationship between them is given by, \[dy. In section 2.2 we explored the meaning and use of the derivative. Finding the slope of a tangent line to a curve (the derivative). For instance, given the function w = g(x,y,z) w = g (x, y,. Differentials Explained Calculus.
From schools.studyrate.in
Differential calculus Defined and explained with examples Study Rate Differentials Explained Calculus When we first looked at derivatives, we used the. In section 2.2 we explored the meaning and use of the derivative. Recall that the derivative of a. Finding the slope of a tangent line to a curve (the derivative). Differentials provide us with a way of estimating the amount a function changes as a result of a small change in. Differentials Explained Calculus.
From www.cuemath.com
Differential Calculus Terms, Formulas, Rules, Examples Differentials Explained Calculus Differential calculus is a branch of calculus involving the study of derivatives that are used to find the instantaneous rate of change of a function using the process of differentiation. When we first looked at derivatives, we used the. For instance, given the function w = g(x,y,z) w = g (x, y, z) the. In section 2.2 we explored the. Differentials Explained Calculus.
From www.media4math.com
DefinitionCalculus TopicsDifferential Equation Media4Math Differentials Explained Calculus When we first looked at derivatives, we used the. This section starts by revisiting some of those ideas. There is a natural extension to functions of three or more variables. In section 2.2 we explored the meaning and use of the derivative. For instance, given the function w = g(x,y,z) w = g (x, y, z) the. Differentials provide us. Differentials Explained Calculus.
From pdfslide.net
(PDF) Basics of Differential Calculus University Of · PDF fileWhy Differentials Explained Calculus When we first looked at derivatives, we used the. In section 2.2 we explored the meaning and use of the derivative. Recall that the derivative of a. There is a natural extension to functions of three or more variables. Differential calculus is a branch of calculus involving the study of derivatives that are used to find the instantaneous rate of. Differentials Explained Calculus.
From ar.inspiredpencil.com
Calculus Derivative Formula Differentials Explained Calculus For instance, given the function w = g(x,y,z) w = g (x, y, z) the. Finding the slope of a tangent line to a curve (the derivative). There is a natural extension to functions of three or more variables. Recall that the derivative of a. This section starts by revisiting some of those ideas. When we first looked at derivatives,. Differentials Explained Calculus.
From diagramlibrarywhereat.z21.web.core.windows.net
The Chain Rule Explained Differentials Explained Calculus Finding the slope of a tangent line to a curve (the derivative). For instance, given the function w = g(x,y,z) w = g (x, y, z) the. Differentials provide us with a way of estimating the amount a function changes as a result of a small change in input values. Differential calculus is a branch of calculus involving the study. Differentials Explained Calculus.
From www.pinterest.com
Applications of Differential Calculus/ differential calculas for 12th Differentials Explained Calculus Finding the slope of a tangent line to a curve (the derivative). Given a function \(y = f\left( x \right)\) we call \(dy\) and \(dx\) differentials and the relationship between them is given by, \[dy. Differentials provide us with a way of estimating the amount a function changes as a result of a small change in input values. This section. Differentials Explained Calculus.
From www.reddit.com
[College Calculus Solving differential equations using series] Please Differentials Explained Calculus Given a function \(y = f\left( x \right)\) we call \(dy\) and \(dx\) differentials and the relationship between them is given by, \[dy. In section 2.2 we explored the meaning and use of the derivative. Finding the slope of a tangent line to a curve (the derivative). Differential calculus is a branch of calculus involving the study of derivatives that. Differentials Explained Calculus.
From slideplayer.com
MAT 3238 Vector Calculus 15.4 Tangent Planes. ppt download Differentials Explained Calculus Differential calculus is a branch of calculus involving the study of derivatives that are used to find the instantaneous rate of change of a function using the process of differentiation. Differentials provide us with a way of estimating the amount a function changes as a result of a small change in input values. In section 2.2 we explored the meaning. Differentials Explained Calculus.
From www.kobo.com
Introduction to Differential Calculus eBook by Ulrich L. Rohde EPUB Differentials Explained Calculus For instance, given the function w = g(x,y,z) w = g (x, y, z) the. Finding the slope of a tangent line to a curve (the derivative). Recall that the derivative of a. This section starts by revisiting some of those ideas. In section 2.2 we explored the meaning and use of the derivative. There is a natural extension to. Differentials Explained Calculus.