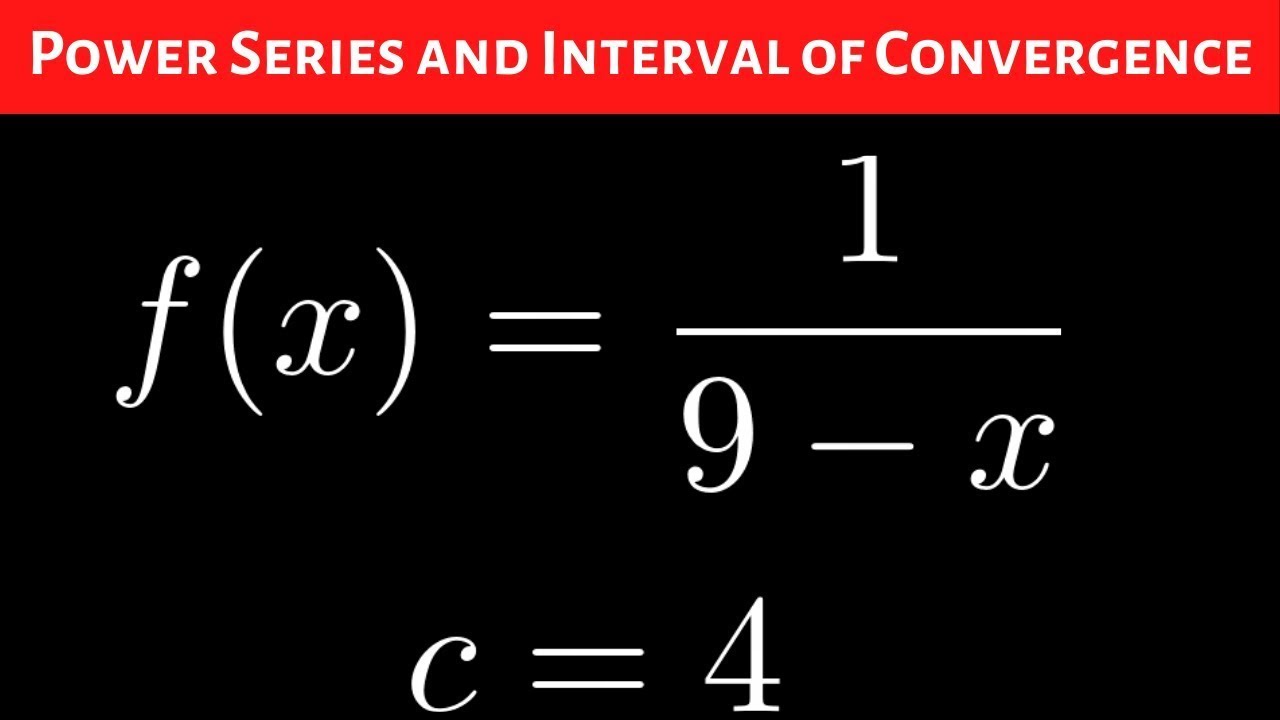Power Series Expansion Region Of Convergence . in other words by (2.1), this series converges if |z−z 0| < |a−z 0| and diverges if |z−z 0| ≥ |a − z 0|. learn how to define and evaluate power series, which are functions that represent the sum of an infinite series of terms. the previous section showed that a power series converges to an analytic function inside its disk of convergence. — learn how to write and analyze power series, which are functions of x x that can be written as infinite sums of. The region of convergence is a disk. series converges for |z| < r, diverges for |z| > r ♣ a power series s = p∞ n=0 a n(z −z0) n is holomorphic in the region of. learn how to define, converge, and represent functions using power series, which are infinite polynomials with variable powers. learn the definition and theorem of the radius of convergence of a power series, and see examples of the ratio test and the root.
from www.youtube.com
learn how to define and evaluate power series, which are functions that represent the sum of an infinite series of terms. series converges for |z| < r, diverges for |z| > r ♣ a power series s = p∞ n=0 a n(z −z0) n is holomorphic in the region of. The region of convergence is a disk. in other words by (2.1), this series converges if |z−z 0| < |a−z 0| and diverges if |z−z 0| ≥ |a − z 0|. — learn how to write and analyze power series, which are functions of x x that can be written as infinite sums of. the previous section showed that a power series converges to an analytic function inside its disk of convergence. learn how to define, converge, and represent functions using power series, which are infinite polynomials with variable powers. learn the definition and theorem of the radius of convergence of a power series, and see examples of the ratio test and the root.
Find the Power Series Centered at c = 4 for f(x) = 1/(9 x) and the
Power Series Expansion Region Of Convergence learn the definition and theorem of the radius of convergence of a power series, and see examples of the ratio test and the root. learn how to define, converge, and represent functions using power series, which are infinite polynomials with variable powers. the previous section showed that a power series converges to an analytic function inside its disk of convergence. learn the definition and theorem of the radius of convergence of a power series, and see examples of the ratio test and the root. — learn how to write and analyze power series, which are functions of x x that can be written as infinite sums of. The region of convergence is a disk. in other words by (2.1), this series converges if |z−z 0| < |a−z 0| and diverges if |z−z 0| ≥ |a − z 0|. series converges for |z| < r, diverges for |z| > r ♣ a power series s = p∞ n=0 a n(z −z0) n is holomorphic in the region of. learn how to define and evaluate power series, which are functions that represent the sum of an infinite series of terms.
From www.youtube.com
Find the Power Series Centered at c = 4 for f(x) = 1/(9 x) and the Power Series Expansion Region Of Convergence learn how to define and evaluate power series, which are functions that represent the sum of an infinite series of terms. The region of convergence is a disk. learn how to define, converge, and represent functions using power series, which are infinite polynomials with variable powers. in other words by (2.1), this series converges if |z−z 0|. Power Series Expansion Region Of Convergence.
From www.youtube.com
Find power series representation for f(x) = 1/(1+x). Determine interval Power Series Expansion Region Of Convergence The region of convergence is a disk. learn the definition and theorem of the radius of convergence of a power series, and see examples of the ratio test and the root. the previous section showed that a power series converges to an analytic function inside its disk of convergence. learn how to define and evaluate power series,. Power Series Expansion Region Of Convergence.
From www.youtube.com
Radius of convergence of a power series solution to differential Power Series Expansion Region Of Convergence the previous section showed that a power series converges to an analytic function inside its disk of convergence. learn how to define and evaluate power series, which are functions that represent the sum of an infinite series of terms. The region of convergence is a disk. — learn how to write and analyze power series, which are. Power Series Expansion Region Of Convergence.
From www.numerade.com
SOLVED Find the power series expansion for the function and simplify Power Series Expansion Region Of Convergence The region of convergence is a disk. in other words by (2.1), this series converges if |z−z 0| < |a−z 0| and diverges if |z−z 0| ≥ |a − z 0|. learn how to define and evaluate power series, which are functions that represent the sum of an infinite series of terms. series converges for |z| <. Power Series Expansion Region Of Convergence.
From www.youtube.com
3 Finding the regions of convergence for power series YouTube Power Series Expansion Region Of Convergence series converges for |z| < r, diverges for |z| > r ♣ a power series s = p∞ n=0 a n(z −z0) n is holomorphic in the region of. the previous section showed that a power series converges to an analytic function inside its disk of convergence. learn how to define and evaluate power series, which are. Power Series Expansion Region Of Convergence.
From www.numerade.com
SOLVEDTutorial Exercise Evaluate the indefinite integral as power Power Series Expansion Region Of Convergence learn how to define, converge, and represent functions using power series, which are infinite polynomials with variable powers. the previous section showed that a power series converges to an analytic function inside its disk of convergence. The region of convergence is a disk. learn how to define and evaluate power series, which are functions that represent the. Power Series Expansion Region Of Convergence.
From www.youtube.com
Power Series Expansions Example 1 YouTube Power Series Expansion Region Of Convergence series converges for |z| < r, diverges for |z| > r ♣ a power series s = p∞ n=0 a n(z −z0) n is holomorphic in the region of. in other words by (2.1), this series converges if |z−z 0| < |a−z 0| and diverges if |z−z 0| ≥ |a − z 0|. the previous section showed. Power Series Expansion Region Of Convergence.
From engineerstutor.com
Inverse z Transform Power Series Expansion Method EngineersTutor Power Series Expansion Region Of Convergence learn how to define and evaluate power series, which are functions that represent the sum of an infinite series of terms. The region of convergence is a disk. — learn how to write and analyze power series, which are functions of x x that can be written as infinite sums of. in other words by (2.1), this. Power Series Expansion Region Of Convergence.
From www.nagwa.com
Question Video Determining the Interval of Convergence for a Rational Power Series Expansion Region Of Convergence learn how to define, converge, and represent functions using power series, which are infinite polynomials with variable powers. — learn how to write and analyze power series, which are functions of x x that can be written as infinite sums of. in other words by (2.1), this series converges if |z−z 0| < |a−z 0| and diverges. Power Series Expansion Region Of Convergence.
From www.youtube.com
RADIUS OF CONVERGENCE OF POWER SERIES 🔥 part 1 YouTube Power Series Expansion Region Of Convergence in other words by (2.1), this series converges if |z−z 0| < |a−z 0| and diverges if |z−z 0| ≥ |a − z 0|. series converges for |z| < r, diverges for |z| > r ♣ a power series s = p∞ n=0 a n(z −z0) n is holomorphic in the region of. The region of convergence is. Power Series Expansion Region Of Convergence.
From www.youtube.com
Lec 20 Mathematical Physics Power Series Expansion Radius of Power Series Expansion Region Of Convergence the previous section showed that a power series converges to an analytic function inside its disk of convergence. The region of convergence is a disk. series converges for |z| < r, diverges for |z| > r ♣ a power series s = p∞ n=0 a n(z −z0) n is holomorphic in the region of. — learn how. Power Series Expansion Region Of Convergence.
From www.youtube.com
Find the Power Series Representation of ln(5 x) and the Radius of Power Series Expansion Region Of Convergence the previous section showed that a power series converges to an analytic function inside its disk of convergence. series converges for |z| < r, diverges for |z| > r ♣ a power series s = p∞ n=0 a n(z −z0) n is holomorphic in the region of. learn the definition and theorem of the radius of convergence. Power Series Expansion Region Of Convergence.
From www.youtube.com
Interval and Radius of Convergence of Power Series SUM( (1)^nx^n/n Power Series Expansion Region Of Convergence — learn how to write and analyze power series, which are functions of x x that can be written as infinite sums of. in other words by (2.1), this series converges if |z−z 0| < |a−z 0| and diverges if |z−z 0| ≥ |a − z 0|. series converges for |z| < r, diverges for |z| >. Power Series Expansion Region Of Convergence.
From www.youtube.com
Power Series Finding The Radius & Interval of Convergence Calculus Power Series Expansion Region Of Convergence learn how to define, converge, and represent functions using power series, which are infinite polynomials with variable powers. learn how to define and evaluate power series, which are functions that represent the sum of an infinite series of terms. in other words by (2.1), this series converges if |z−z 0| < |a−z 0| and diverges if |z−z. Power Series Expansion Region Of Convergence.
From ramanujan.math.trinity.edu
Convergence of Power Series Power Series Expansion Region Of Convergence in other words by (2.1), this series converges if |z−z 0| < |a−z 0| and diverges if |z−z 0| ≥ |a − z 0|. The region of convergence is a disk. the previous section showed that a power series converges to an analytic function inside its disk of convergence. learn how to define, converge, and represent functions. Power Series Expansion Region Of Convergence.
From www.youtube.com
Interval and Radius of Convergence of the Power Series SUM((1/(n^2 + n Power Series Expansion Region Of Convergence series converges for |z| < r, diverges for |z| > r ♣ a power series s = p∞ n=0 a n(z −z0) n is holomorphic in the region of. learn how to define, converge, and represent functions using power series, which are infinite polynomials with variable powers. the previous section showed that a power series converges to. Power Series Expansion Region Of Convergence.
From www.numerade.com
SOLVEDGiven that 1 xn with convergence in (1, 1), n =0 find the power Power Series Expansion Region Of Convergence learn how to define, converge, and represent functions using power series, which are infinite polynomials with variable powers. the previous section showed that a power series converges to an analytic function inside its disk of convergence. series converges for |z| < r, diverges for |z| > r ♣ a power series s = p∞ n=0 a n(z. Power Series Expansion Region Of Convergence.
From www.nagwa.com
Question Video Power Series and Radius of Convergence Nagwa Power Series Expansion Region Of Convergence learn the definition and theorem of the radius of convergence of a power series, and see examples of the ratio test and the root. in other words by (2.1), this series converges if |z−z 0| < |a−z 0| and diverges if |z−z 0| ≥ |a − z 0|. series converges for |z| < r, diverges for |z|. Power Series Expansion Region Of Convergence.
From www.youtube.com
How to Find the Interval of Convergence of a Power Series SUM((1)^(n Power Series Expansion Region Of Convergence learn how to define and evaluate power series, which are functions that represent the sum of an infinite series of terms. learn the definition and theorem of the radius of convergence of a power series, and see examples of the ratio test and the root. — learn how to write and analyze power series, which are functions. Power Series Expansion Region Of Convergence.
From www.youtube.com
Radius of Convergence for a Power Series YouTube Power Series Expansion Region Of Convergence the previous section showed that a power series converges to an analytic function inside its disk of convergence. learn how to define, converge, and represent functions using power series, which are infinite polynomials with variable powers. The region of convergence is a disk. series converges for |z| < r, diverges for |z| > r ♣ a power. Power Series Expansion Region Of Convergence.
From www.numerade.com
SOLVED Suppose that the radius of convergence of the power series cnxn Power Series Expansion Region Of Convergence The region of convergence is a disk. learn the definition and theorem of the radius of convergence of a power series, and see examples of the ratio test and the root. learn how to define and evaluate power series, which are functions that represent the sum of an infinite series of terms. series converges for |z| <. Power Series Expansion Region Of Convergence.
From www.scribd.com
Power Series Radius, Center and Interval of Convergence in The Power Power Series Expansion Region Of Convergence learn how to define and evaluate power series, which are functions that represent the sum of an infinite series of terms. the previous section showed that a power series converges to an analytic function inside its disk of convergence. in other words by (2.1), this series converges if |z−z 0| < |a−z 0| and diverges if |z−z. Power Series Expansion Region Of Convergence.
From studylib.net
Lecture 7 Power series expansions Power Series Expansion Region Of Convergence learn the definition and theorem of the radius of convergence of a power series, and see examples of the ratio test and the root. learn how to define and evaluate power series, which are functions that represent the sum of an infinite series of terms. series converges for |z| < r, diverges for |z| > r ♣. Power Series Expansion Region Of Convergence.
From engineerstutor.com
Inverse z Transform Power Series Expansion Method EngineersTutor Power Series Expansion Region Of Convergence learn how to define and evaluate power series, which are functions that represent the sum of an infinite series of terms. the previous section showed that a power series converges to an analytic function inside its disk of convergence. learn how to define, converge, and represent functions using power series, which are infinite polynomials with variable powers.. Power Series Expansion Region Of Convergence.
From www.youtube.com
Find a power series representation of ln(1+x) and its radius of Power Series Expansion Region Of Convergence in other words by (2.1), this series converges if |z−z 0| < |a−z 0| and diverges if |z−z 0| ≥ |a − z 0|. learn how to define, converge, and represent functions using power series, which are infinite polynomials with variable powers. The region of convergence is a disk. learn how to define and evaluate power series,. Power Series Expansion Region Of Convergence.
From math.stackexchange.com
real analysis power series uniformly convergence on its radius of Power Series Expansion Region Of Convergence series converges for |z| < r, diverges for |z| > r ♣ a power series s = p∞ n=0 a n(z −z0) n is holomorphic in the region of. in other words by (2.1), this series converges if |z−z 0| < |a−z 0| and diverges if |z−z 0| ≥ |a − z 0|. The region of convergence is. Power Series Expansion Region Of Convergence.
From www.youtube.com
Find power series representation for f(x) = ln (5x). Determine radius Power Series Expansion Region Of Convergence learn how to define, converge, and represent functions using power series, which are infinite polynomials with variable powers. series converges for |z| < r, diverges for |z| > r ♣ a power series s = p∞ n=0 a n(z −z0) n is holomorphic in the region of. — learn how to write and analyze power series, which. Power Series Expansion Region Of Convergence.
From www.youtube.com
Milne Thomson method Power series expansion of Complex Function Power Series Expansion Region Of Convergence — learn how to write and analyze power series, which are functions of x x that can be written as infinite sums of. The region of convergence is a disk. series converges for |z| < r, diverges for |z| > r ♣ a power series s = p∞ n=0 a n(z −z0) n is holomorphic in the region. Power Series Expansion Region Of Convergence.
From www.youtube.com
Ex 1 Interval of Convergence for Power Series (Centered at 0) YouTube Power Series Expansion Region Of Convergence The region of convergence is a disk. in other words by (2.1), this series converges if |z−z 0| < |a−z 0| and diverges if |z−z 0| ≥ |a − z 0|. the previous section showed that a power series converges to an analytic function inside its disk of convergence. learn how to define and evaluate power series,. Power Series Expansion Region Of Convergence.
From www.youtube.com
Power Series Finding the Radius and Interval of Convergence Of Power Power Series Expansion Region Of Convergence learn how to define and evaluate power series, which are functions that represent the sum of an infinite series of terms. in other words by (2.1), this series converges if |z−z 0| < |a−z 0| and diverges if |z−z 0| ≥ |a − z 0|. The region of convergence is a disk. learn how to define, converge,. Power Series Expansion Region Of Convergence.
From www.slideserve.com
PPT 2414 Calculus II Chapter 9(2) Power Series Convergence of Power Power Series Expansion Region Of Convergence learn how to define and evaluate power series, which are functions that represent the sum of an infinite series of terms. learn the definition and theorem of the radius of convergence of a power series, and see examples of the ratio test and the root. series converges for |z| < r, diverges for |z| > r ♣. Power Series Expansion Region Of Convergence.
From www.youtube.com
Use the binomial series to expand (1x)^(2/3) as a power series. State Power Series Expansion Region Of Convergence — learn how to write and analyze power series, which are functions of x x that can be written as infinite sums of. The region of convergence is a disk. learn the definition and theorem of the radius of convergence of a power series, and see examples of the ratio test and the root. in other words. Power Series Expansion Region Of Convergence.
From calcworkshop.com
Power Series Power Series Expansion Region Of Convergence learn how to define, converge, and represent functions using power series, which are infinite polynomials with variable powers. — learn how to write and analyze power series, which are functions of x x that can be written as infinite sums of. The region of convergence is a disk. learn the definition and theorem of the radius of. Power Series Expansion Region Of Convergence.
From www.youtube.com
Review Question 8 Power Series, Radius and Interval of Convergence Power Series Expansion Region Of Convergence the previous section showed that a power series converges to an analytic function inside its disk of convergence. in other words by (2.1), this series converges if |z−z 0| < |a−z 0| and diverges if |z−z 0| ≥ |a − z 0|. learn the definition and theorem of the radius of convergence of a power series, and. Power Series Expansion Region Of Convergence.
From www.youtube.com
Find the radius of convergence of a power series YouTube Power Series Expansion Region Of Convergence learn how to define and evaluate power series, which are functions that represent the sum of an infinite series of terms. the previous section showed that a power series converges to an analytic function inside its disk of convergence. learn how to define, converge, and represent functions using power series, which are infinite polynomials with variable powers.. Power Series Expansion Region Of Convergence.