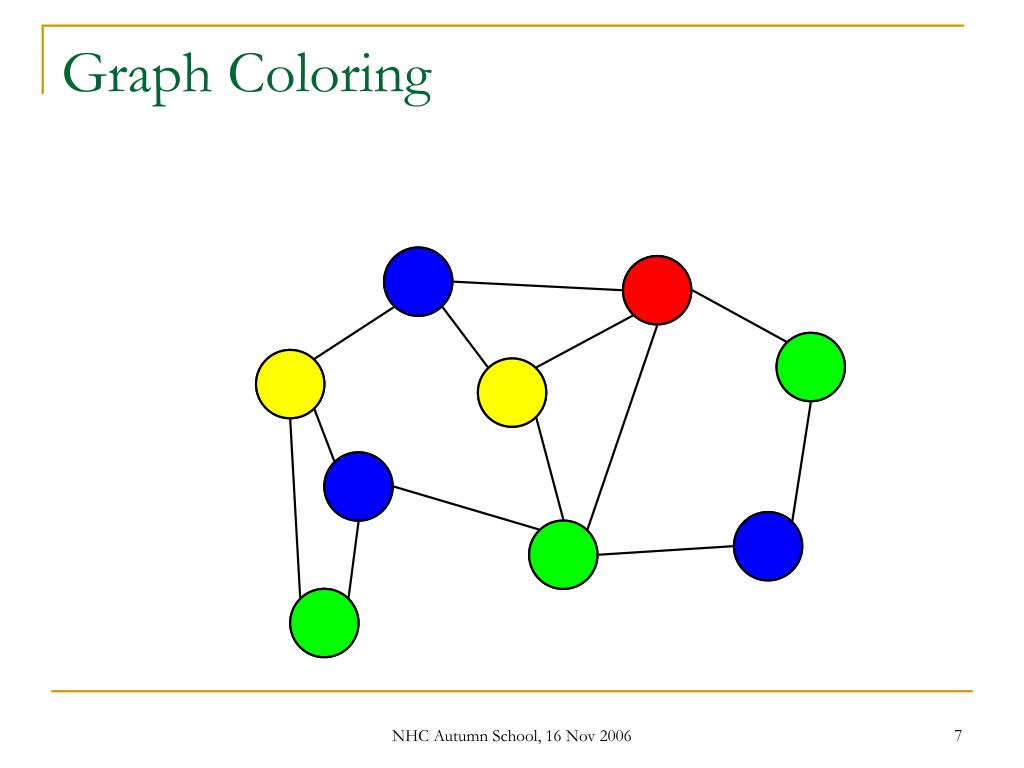
Graph Coloring Example Problems . Clearly the interesting quantity is the minimum. There’s a couple specific versions of the theoretical problem. Given a graph \(g\) it is easy to find a proper coloring: Give every vertex a different color. Graph coloring refers to the problem of coloring vertices of a graph in such a way that no two adjacent vertices have the same color. First, we’ll define the problem. I could give you a graph and ask you for its chromatic number. In this article, we will solve the graph coloring problem using the constructive heuristic dsatur (brélaz, 1979) and an integer linear programming model using.
from www.slideserve.com
Clearly the interesting quantity is the minimum. Graph coloring refers to the problem of coloring vertices of a graph in such a way that no two adjacent vertices have the same color. I could give you a graph and ask you for its chromatic number. Given a graph \(g\) it is easy to find a proper coloring: First, we’ll define the problem. In this article, we will solve the graph coloring problem using the constructive heuristic dsatur (brélaz, 1979) and an integer linear programming model using. Give every vertex a different color. There’s a couple specific versions of the theoretical problem.
PPT Approximation Techniques for Coloring Problems PowerPoint Presentation ID27673
Graph Coloring Example Problems Clearly the interesting quantity is the minimum. Given a graph \(g\) it is easy to find a proper coloring: First, we’ll define the problem. In this article, we will solve the graph coloring problem using the constructive heuristic dsatur (brélaz, 1979) and an integer linear programming model using. I could give you a graph and ask you for its chromatic number. Give every vertex a different color. There’s a couple specific versions of the theoretical problem. Graph coloring refers to the problem of coloring vertices of a graph in such a way that no two adjacent vertices have the same color. Clearly the interesting quantity is the minimum.
From antiguadominic.medium.com
Graph coloring using adjacency matrix — Discrete Math Problem by Dominic Antigua Medium Graph Coloring Example Problems First, we’ll define the problem. Give every vertex a different color. Graph coloring refers to the problem of coloring vertices of a graph in such a way that no two adjacent vertices have the same color. Clearly the interesting quantity is the minimum. In this article, we will solve the graph coloring problem using the constructive heuristic dsatur (brélaz, 1979). Graph Coloring Example Problems.
From www.worksheeto.com
13 Graph Coloring Worksheets / Graph Coloring Example Problems Clearly the interesting quantity is the minimum. In this article, we will solve the graph coloring problem using the constructive heuristic dsatur (brélaz, 1979) and an integer linear programming model using. There’s a couple specific versions of the theoretical problem. Give every vertex a different color. First, we’ll define the problem. Given a graph \(g\) it is easy to find. Graph Coloring Example Problems.
From www.researchgate.net
1 Graph Coloring Example 1 Graph Coloring Example shows an example of... Download Scientific Graph Coloring Example Problems Graph coloring refers to the problem of coloring vertices of a graph in such a way that no two adjacent vertices have the same color. Given a graph \(g\) it is easy to find a proper coloring: I could give you a graph and ask you for its chromatic number. First, we’ll define the problem. Clearly the interesting quantity is. Graph Coloring Example Problems.
From www.chegg.com
1. The graph coloring problem is the task of Graph Coloring Example Problems I could give you a graph and ask you for its chromatic number. Give every vertex a different color. First, we’ll define the problem. In this article, we will solve the graph coloring problem using the constructive heuristic dsatur (brélaz, 1979) and an integer linear programming model using. Clearly the interesting quantity is the minimum. There’s a couple specific versions. Graph Coloring Example Problems.
From www.youtube.com
Graph Coloring problem using backtracking lecture55/ADA YouTube Graph Coloring Example Problems Graph coloring refers to the problem of coloring vertices of a graph in such a way that no two adjacent vertices have the same color. Given a graph \(g\) it is easy to find a proper coloring: I could give you a graph and ask you for its chromatic number. Give every vertex a different color. There’s a couple specific. Graph Coloring Example Problems.
From www.scaler.com
Graph Coloring Problem Scalar Topics Graph Coloring Example Problems I could give you a graph and ask you for its chromatic number. Give every vertex a different color. Graph coloring refers to the problem of coloring vertices of a graph in such a way that no two adjacent vertices have the same color. Given a graph \(g\) it is easy to find a proper coloring: Clearly the interesting quantity. Graph Coloring Example Problems.
From worksheetlistvi.z21.web.core.windows.net
Math Coloring Pages Graphing Graph Coloring Example Problems There’s a couple specific versions of the theoretical problem. In this article, we will solve the graph coloring problem using the constructive heuristic dsatur (brélaz, 1979) and an integer linear programming model using. I could give you a graph and ask you for its chromatic number. Give every vertex a different color. Given a graph \(g\) it is easy to. Graph Coloring Example Problems.
From www.interviewbit.com
Graph Coloring Problem InterviewBit Graph Coloring Example Problems Clearly the interesting quantity is the minimum. I could give you a graph and ask you for its chromatic number. In this article, we will solve the graph coloring problem using the constructive heuristic dsatur (brélaz, 1979) and an integer linear programming model using. Given a graph \(g\) it is easy to find a proper coloring: First, we’ll define the. Graph Coloring Example Problems.
From calcworkshop.com
Graph Coloring (Fully Explained in Detail w/ StepbyStep Examples!) Graph Coloring Example Problems Given a graph \(g\) it is easy to find a proper coloring: In this article, we will solve the graph coloring problem using the constructive heuristic dsatur (brélaz, 1979) and an integer linear programming model using. Give every vertex a different color. There’s a couple specific versions of the theoretical problem. First, we’ll define the problem. I could give you. Graph Coloring Example Problems.
From www.interviewbit.com
Graph Coloring Problem InterviewBit Graph Coloring Example Problems Give every vertex a different color. Clearly the interesting quantity is the minimum. I could give you a graph and ask you for its chromatic number. First, we’ll define the problem. Given a graph \(g\) it is easy to find a proper coloring: In this article, we will solve the graph coloring problem using the constructive heuristic dsatur (brélaz, 1979). Graph Coloring Example Problems.
From algodaily.com
AlgoDaily The Two Coloring Graph Problem Graph Coloring Example Problems Clearly the interesting quantity is the minimum. First, we’ll define the problem. I could give you a graph and ask you for its chromatic number. Graph coloring refers to the problem of coloring vertices of a graph in such a way that no two adjacent vertices have the same color. There’s a couple specific versions of the theoretical problem. Give. Graph Coloring Example Problems.
From educativeprintable.com
Useful Graph Coloring Pages Educative Printable Graph Coloring Example Problems In this article, we will solve the graph coloring problem using the constructive heuristic dsatur (brélaz, 1979) and an integer linear programming model using. Give every vertex a different color. Graph coloring refers to the problem of coloring vertices of a graph in such a way that no two adjacent vertices have the same color. Given a graph \(g\) it. Graph Coloring Example Problems.
From www.youtube.com
Graph Colouring Problem Backtracking YouTube Graph Coloring Example Problems Given a graph \(g\) it is easy to find a proper coloring: Clearly the interesting quantity is the minimum. In this article, we will solve the graph coloring problem using the constructive heuristic dsatur (brélaz, 1979) and an integer linear programming model using. Give every vertex a different color. Graph coloring refers to the problem of coloring vertices of a. Graph Coloring Example Problems.
From www.chegg.com
Solved 1. The graph coloring problem is the task of Graph Coloring Example Problems Clearly the interesting quantity is the minimum. There’s a couple specific versions of the theoretical problem. First, we’ll define the problem. In this article, we will solve the graph coloring problem using the constructive heuristic dsatur (brélaz, 1979) and an integer linear programming model using. Given a graph \(g\) it is easy to find a proper coloring: I could give. Graph Coloring Example Problems.
From www.scaler.com
Graph Coloring Problem Scalar Topics Graph Coloring Example Problems Graph coloring refers to the problem of coloring vertices of a graph in such a way that no two adjacent vertices have the same color. Clearly the interesting quantity is the minimum. First, we’ll define the problem. There’s a couple specific versions of the theoretical problem. In this article, we will solve the graph coloring problem using the constructive heuristic. Graph Coloring Example Problems.
From www.youtube.com
DAAModule5Graph Coloring Problem YouTube Graph Coloring Example Problems Graph coloring refers to the problem of coloring vertices of a graph in such a way that no two adjacent vertices have the same color. I could give you a graph and ask you for its chromatic number. Give every vertex a different color. Clearly the interesting quantity is the minimum. Given a graph \(g\) it is easy to find. Graph Coloring Example Problems.
From coloring-draw.pages.dev
22++ Graph coloring in algorithm ideas https//coloringdraw.pages.dev Graph Coloring Example Problems I could give you a graph and ask you for its chromatic number. There’s a couple specific versions of the theoretical problem. In this article, we will solve the graph coloring problem using the constructive heuristic dsatur (brélaz, 1979) and an integer linear programming model using. Clearly the interesting quantity is the minimum. Given a graph \(g\) it is easy. Graph Coloring Example Problems.
From www.pinterest.ca
Free Printable Colored Graph Worksheets Kindergarten math, Graphing worksheets, Preschool math Graph Coloring Example Problems Give every vertex a different color. Clearly the interesting quantity is the minimum. In this article, we will solve the graph coloring problem using the constructive heuristic dsatur (brélaz, 1979) and an integer linear programming model using. Graph coloring refers to the problem of coloring vertices of a graph in such a way that no two adjacent vertices have the. Graph Coloring Example Problems.
From www.youtube.com
Graph coloring problem using backtracking YouTube Graph Coloring Example Problems Given a graph \(g\) it is easy to find a proper coloring: Clearly the interesting quantity is the minimum. In this article, we will solve the graph coloring problem using the constructive heuristic dsatur (brélaz, 1979) and an integer linear programming model using. Give every vertex a different color. Graph coloring refers to the problem of coloring vertices of a. Graph Coloring Example Problems.
From www.slideshare.net
Graph coloring problem Graph Coloring Example Problems First, we’ll define the problem. Give every vertex a different color. Clearly the interesting quantity is the minimum. In this article, we will solve the graph coloring problem using the constructive heuristic dsatur (brélaz, 1979) and an integer linear programming model using. There’s a couple specific versions of the theoretical problem. Graph coloring refers to the problem of coloring vertices. Graph Coloring Example Problems.
From pencilprogrammer.com
Graph Coloring Algorithm using Backtracking Pencil Programmer Graph Coloring Example Problems I could give you a graph and ask you for its chromatic number. Graph coloring refers to the problem of coloring vertices of a graph in such a way that no two adjacent vertices have the same color. There’s a couple specific versions of the theoretical problem. First, we’ll define the problem. Given a graph \(g\) it is easy to. Graph Coloring Example Problems.
From www.youtube.com
Graph coloring YouTube Graph Coloring Example Problems First, we’ll define the problem. Graph coloring refers to the problem of coloring vertices of a graph in such a way that no two adjacent vertices have the same color. Give every vertex a different color. There’s a couple specific versions of the theoretical problem. Clearly the interesting quantity is the minimum. In this article, we will solve the graph. Graph Coloring Example Problems.
From www.youtube.com
Graph Coloring 7 Problems on Graph Coloring YouTube Graph Coloring Example Problems Graph coloring refers to the problem of coloring vertices of a graph in such a way that no two adjacent vertices have the same color. There’s a couple specific versions of the theoretical problem. In this article, we will solve the graph coloring problem using the constructive heuristic dsatur (brélaz, 1979) and an integer linear programming model using. First, we’ll. Graph Coloring Example Problems.
From coloring-draw.pages.dev
40++ Graph coloring problem using backtracking info https//coloringdraw.pages.dev Graph Coloring Example Problems There’s a couple specific versions of the theoretical problem. Give every vertex a different color. Given a graph \(g\) it is easy to find a proper coloring: I could give you a graph and ask you for its chromatic number. In this article, we will solve the graph coloring problem using the constructive heuristic dsatur (brélaz, 1979) and an integer. Graph Coloring Example Problems.
From www.interviewbit.com
Graph Coloring Problem InterviewBit Graph Coloring Example Problems Give every vertex a different color. In this article, we will solve the graph coloring problem using the constructive heuristic dsatur (brélaz, 1979) and an integer linear programming model using. Clearly the interesting quantity is the minimum. There’s a couple specific versions of the theoretical problem. First, we’ll define the problem. I could give you a graph and ask you. Graph Coloring Example Problems.
From www.researchgate.net
An example of graph coloring problem Download Scientific Diagram Graph Coloring Example Problems Clearly the interesting quantity is the minimum. Give every vertex a different color. Given a graph \(g\) it is easy to find a proper coloring: Graph coloring refers to the problem of coloring vertices of a graph in such a way that no two adjacent vertices have the same color. I could give you a graph and ask you for. Graph Coloring Example Problems.
From antiguadominic.medium.com
Graph coloring using adjacency matrix — Discrete Math Problem by Dominic Antigua Medium Graph Coloring Example Problems In this article, we will solve the graph coloring problem using the constructive heuristic dsatur (brélaz, 1979) and an integer linear programming model using. Graph coloring refers to the problem of coloring vertices of a graph in such a way that no two adjacent vertices have the same color. There’s a couple specific versions of the theoretical problem. First, we’ll. Graph Coloring Example Problems.
From www.sketchite.com
Graph Coloring Backtracking Coloring Pages Graph Coloring Example Problems In this article, we will solve the graph coloring problem using the constructive heuristic dsatur (brélaz, 1979) and an integer linear programming model using. First, we’ll define the problem. Given a graph \(g\) it is easy to find a proper coloring: Graph coloring refers to the problem of coloring vertices of a graph in such a way that no two. Graph Coloring Example Problems.
From www.slideshare.net
0015.register allocationgraphcoloring Graph Coloring Example Problems Given a graph \(g\) it is easy to find a proper coloring: In this article, we will solve the graph coloring problem using the constructive heuristic dsatur (brélaz, 1979) and an integer linear programming model using. Give every vertex a different color. First, we’ll define the problem. Clearly the interesting quantity is the minimum. Graph coloring refers to the problem. Graph Coloring Example Problems.
From www.slideserve.com
PPT Approximation Techniques for Coloring Problems PowerPoint Presentation ID27673 Graph Coloring Example Problems First, we’ll define the problem. Give every vertex a different color. Given a graph \(g\) it is easy to find a proper coloring: Clearly the interesting quantity is the minimum. I could give you a graph and ask you for its chromatic number. There’s a couple specific versions of the theoretical problem. Graph coloring refers to the problem of coloring. Graph Coloring Example Problems.
From nl.pinterest.com
Useful Graph Coloring Pages Educative Printable Coloring pages, Graphing, Fun games for kids Graph Coloring Example Problems Clearly the interesting quantity is the minimum. In this article, we will solve the graph coloring problem using the constructive heuristic dsatur (brélaz, 1979) and an integer linear programming model using. Given a graph \(g\) it is easy to find a proper coloring: There’s a couple specific versions of the theoretical problem. Graph coloring refers to the problem of coloring. Graph Coloring Example Problems.
From www.youtube.com
Coloring Maps Using Graphs & the Four Color Problem YouTube Graph Coloring Example Problems Clearly the interesting quantity is the minimum. Given a graph \(g\) it is easy to find a proper coloring: First, we’ll define the problem. In this article, we will solve the graph coloring problem using the constructive heuristic dsatur (brélaz, 1979) and an integer linear programming model using. Graph coloring refers to the problem of coloring vertices of a graph. Graph Coloring Example Problems.
From www.slideserve.com
PPT Graph Coloring Problem PowerPoint Presentation, free download ID3563511 Graph Coloring Example Problems Clearly the interesting quantity is the minimum. First, we’ll define the problem. I could give you a graph and ask you for its chromatic number. Give every vertex a different color. In this article, we will solve the graph coloring problem using the constructive heuristic dsatur (brélaz, 1979) and an integer linear programming model using. There’s a couple specific versions. Graph Coloring Example Problems.
From www.slideshare.net
Graph coloring problem Graph Coloring Example Problems Graph coloring refers to the problem of coloring vertices of a graph in such a way that no two adjacent vertices have the same color. I could give you a graph and ask you for its chromatic number. Given a graph \(g\) it is easy to find a proper coloring: In this article, we will solve the graph coloring problem. Graph Coloring Example Problems.
From www.youtube.com
BACKTRACKING GRAPH COLORING PROBLEM WITH EXAMPLE YouTube Graph Coloring Example Problems There’s a couple specific versions of the theoretical problem. Graph coloring refers to the problem of coloring vertices of a graph in such a way that no two adjacent vertices have the same color. Give every vertex a different color. First, we’ll define the problem. In this article, we will solve the graph coloring problem using the constructive heuristic dsatur. Graph Coloring Example Problems.