Distribution Of X Bar Values . It is a critical concept in. Let’s look at a simulation: The distribution of sample means is the distribution that results when we find the means of all. The expected value, the standard deviation and the. There are three things we need to know to fully describe a probability distribution of $\bar{x}$: The sample mean is a random variable; If \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from a \(n(\mu, \sigma^2)\) population, then the sample mean:. The distribution of sample means. As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes.
from www.numerade.com
The distribution of sample means. The distribution of sample means is the distribution that results when we find the means of all. There are three things we need to know to fully describe a probability distribution of $\bar{x}$: The expected value, the standard deviation and the. If \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from a \(n(\mu, \sigma^2)\) population, then the sample mean:. It is a critical concept in. As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. Let’s look at a simulation: The sample mean is a random variable;
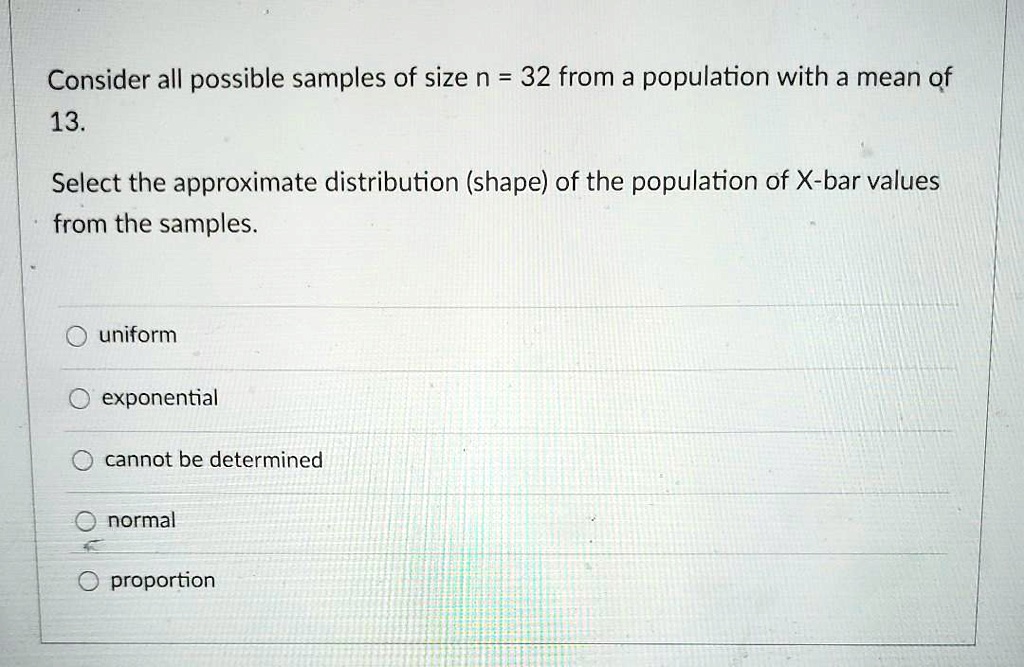
SOLVED Consider all possible samples of size n = 32 from a population with a mean of 13. Select
Distribution Of X Bar Values As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. Let’s look at a simulation: The expected value, the standard deviation and the. The sample mean is a random variable; It is a critical concept in. As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. The distribution of sample means is the distribution that results when we find the means of all. There are three things we need to know to fully describe a probability distribution of $\bar{x}$: If \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from a \(n(\mu, \sigma^2)\) population, then the sample mean:. The distribution of sample means.
From www.integral-concepts.com
What is a good way to select subgroup size for an Xbar Chart? Integral Concepts Distribution Of X Bar Values Let’s look at a simulation: It is a critical concept in. The distribution of sample means. As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. If \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from a \(n(\mu, \sigma^2)\) population, then the sample mean:. The expected value, the standard deviation and. Distribution Of X Bar Values.
From isg.com.sa
Discrete Probability Distribution Overview And Examples, 58 OFF Distribution Of X Bar Values The expected value, the standard deviation and the. The distribution of sample means is the distribution that results when we find the means of all. The distribution of sample means. Let’s look at a simulation: The sample mean is a random variable; If \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from a \(n(\mu, \sigma^2)\). Distribution Of X Bar Values.
From www.youtube.com
Sampling Distribution of xbar Oct 25 2020 YouTube Distribution Of X Bar Values If \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from a \(n(\mu, \sigma^2)\) population, then the sample mean:. The distribution of sample means. The expected value, the standard deviation and the. As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. It is a critical concept in. The distribution of sample. Distribution Of X Bar Values.
From study.com
Probability Distribution Graphs Discrete & Continuous Lesson Distribution Of X Bar Values As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. The distribution of sample means. There are three things we need to know to fully describe a probability distribution of $\bar{x}$: If \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from a \(n(\mu, \sigma^2)\) population, then the sample mean:. The expected. Distribution Of X Bar Values.
From bookdown.org
Chapter 6 Introduction to Confidence Intervals Introduction to Statistics Distribution Of X Bar Values Let’s look at a simulation: The distribution of sample means is the distribution that results when we find the means of all. The expected value, the standard deviation and the. As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. There are three things we need to know to fully describe a probability distribution of $\bar{x}$:. Distribution Of X Bar Values.
From moe4.de
X Bar Distribution Of X Bar Values The expected value, the standard deviation and the. If \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from a \(n(\mu, \sigma^2)\) population, then the sample mean:. It is a critical concept in. Let’s look at a simulation: The sample mean is a random variable; The distribution of sample means is the distribution that results when. Distribution Of X Bar Values.
From calcworkshop.com
Discrete Random Variable (11+ StepbyStep Examples!) Distribution Of X Bar Values As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. The distribution of sample means. It is a critical concept in. The sample mean is a random variable; Let’s look at a simulation: The expected value, the standard deviation and the. The distribution of sample means is the distribution that results when we find the means. Distribution Of X Bar Values.
From www.scribbr.com
The Standard Normal Distribution Examples, Explanations, Uses Distribution Of X Bar Values As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. The distribution of sample means. The distribution of sample means is the distribution that results when we find the means of all. There are three things we need to know to fully describe a probability distribution of $\bar{x}$: The sample mean is a random variable; Let’s. Distribution Of X Bar Values.
From www.youtube.com
Part 1 Maximum Likelihood Estimator x bar vs mu intuition (Normal Distribution) YouTube Distribution Of X Bar Values It is a critical concept in. If \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from a \(n(\mu, \sigma^2)\) population, then the sample mean:. The sample mean is a random variable; Let’s look at a simulation: The distribution of sample means is the distribution that results when we find the means of all. The distribution. Distribution Of X Bar Values.
From www.statology.org
Symmetric Distribution Definition + Examples Distribution Of X Bar Values It is a critical concept in. The sample mean is a random variable; As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. Let’s look at a simulation: The expected value, the standard deviation and the. The distribution of sample means. There are three things we need to know to fully describe a probability distribution of. Distribution Of X Bar Values.
From www.investopedia.com
The Normal Distribution Table Definition Distribution Of X Bar Values The sample mean is a random variable; There are three things we need to know to fully describe a probability distribution of $\bar{x}$: Let’s look at a simulation: The expected value, the standard deviation and the. The distribution of sample means is the distribution that results when we find the means of all. As such it is written \(\bar{x}\), and. Distribution Of X Bar Values.
From www.investopedia.com
Probability Distribution Explained Types and Uses in Investing Distribution Of X Bar Values The expected value, the standard deviation and the. The sample mean is a random variable; As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. The distribution of sample means is the distribution that results when we find the means of all. Let’s look at a simulation: If \(x_1, x_2, \ldots, x_n\) are observations of a. Distribution Of X Bar Values.
From www.statology.org
How to Compare Histograms (With Examples) Distribution Of X Bar Values Let’s look at a simulation: It is a critical concept in. If \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from a \(n(\mu, \sigma^2)\) population, then the sample mean:. The distribution of sample means is the distribution that results when we find the means of all. As such it is written \(\bar{x}\), and \(\bar{x}\) stands. Distribution Of X Bar Values.
From www.scribbr.com
Normal Distribution Examples, Formulas, & Uses Distribution Of X Bar Values As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. Let’s look at a simulation: It is a critical concept in. The sample mean is a random variable; The expected value, the standard deviation and the. The distribution of sample means is the distribution that results when we find the means of all. The distribution of. Distribution Of X Bar Values.
From www.slideserve.com
PPT Chapter 6 Part 3 PowerPoint Presentation, free download ID205485 Distribution Of X Bar Values The expected value, the standard deviation and the. It is a critical concept in. The distribution of sample means is the distribution that results when we find the means of all. The distribution of sample means. As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. If \(x_1, x_2, \ldots, x_n\) are observations of a random. Distribution Of X Bar Values.
From www.slideserve.com
PPT Sampling distributions for sample means PowerPoint Presentation, free download ID654394 Distribution Of X Bar Values As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. It is a critical concept in. There are three things we need to know to fully describe a probability distribution of $\bar{x}$: The sample mean is a random variable; The distribution of sample means. The expected value, the standard deviation and the. The distribution of sample. Distribution Of X Bar Values.
From www.integral-concepts.com
What is a good way to select subgroup size for an Xbar Chart? Integral Concepts Distribution Of X Bar Values If \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from a \(n(\mu, \sigma^2)\) population, then the sample mean:. The distribution of sample means is the distribution that results when we find the means of all. It is a critical concept in. The sample mean is a random variable; The expected value, the standard deviation and. Distribution Of X Bar Values.
From slideplayer.com
Continuous Probability Distributions ppt download Distribution Of X Bar Values Let’s look at a simulation: If \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from a \(n(\mu, \sigma^2)\) population, then the sample mean:. It is a critical concept in. As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. There are three things we need to know to fully describe a. Distribution Of X Bar Values.
From www.slideserve.com
PPT 5 Normal Probability Distributions PowerPoint Presentation, free download ID5758017 Distribution Of X Bar Values The distribution of sample means. The distribution of sample means is the distribution that results when we find the means of all. There are three things we need to know to fully describe a probability distribution of $\bar{x}$: If \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from a \(n(\mu, \sigma^2)\) population, then the sample. Distribution Of X Bar Values.
From bookdown.org
Chapter 4 Sampling Distribution of \(\bar{X}\) Introduction to Statistical Methodology, Second Distribution Of X Bar Values There are three things we need to know to fully describe a probability distribution of $\bar{x}$: The distribution of sample means is the distribution that results when we find the means of all. The expected value, the standard deviation and the. It is a critical concept in. As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it. Distribution Of X Bar Values.
From andrewmilivojevich.com
Xbar and R Chart Formula and Constants The Definitive Guide Distribution Of X Bar Values The sample mean is a random variable; Let’s look at a simulation: It is a critical concept in. The distribution of sample means. There are three things we need to know to fully describe a probability distribution of $\bar{x}$: As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. The expected value, the standard deviation and. Distribution Of X Bar Values.
From www.cqeacademy.com
Statistical Process Control (SPC) CQE Academy Distribution Of X Bar Values If \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from a \(n(\mu, \sigma^2)\) population, then the sample mean:. The distribution of sample means. The expected value, the standard deviation and the. As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. The sample mean is a random variable; Let’s look at. Distribution Of X Bar Values.
From www.youtube.com
Distribution Tables and Bar Charts for Discrete Random Variables YouTube Distribution Of X Bar Values The distribution of sample means is the distribution that results when we find the means of all. The distribution of sample means. The expected value, the standard deviation and the. Let’s look at a simulation: There are three things we need to know to fully describe a probability distribution of $\bar{x}$: The sample mean is a random variable; If \(x_1,. Distribution Of X Bar Values.
From todon.weebly.com
Distribution of xbar todon Distribution Of X Bar Values It is a critical concept in. The sample mean is a random variable; The distribution of sample means. There are three things we need to know to fully describe a probability distribution of $\bar{x}$: If \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from a \(n(\mu, \sigma^2)\) population, then the sample mean:. As such it. Distribution Of X Bar Values.
From slideplayer.com
Essential Statistics Sampling Distributions ppt download Distribution Of X Bar Values The distribution of sample means. The expected value, the standard deviation and the. Let’s look at a simulation: The distribution of sample means is the distribution that results when we find the means of all. As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. It is a critical concept in. There are three things we. Distribution Of X Bar Values.
From www.scribbr.com
The Standard Normal Distribution Examples, Explanations, Uses Distribution Of X Bar Values It is a critical concept in. Let’s look at a simulation: The sample mean is a random variable; The expected value, the standard deviation and the. If \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from a \(n(\mu, \sigma^2)\) population, then the sample mean:. The distribution of sample means. There are three things we need. Distribution Of X Bar Values.
From www.numerade.com
SOLVED Consider all possible samples of size n = 32 from a population with a mean of 13. Select Distribution Of X Bar Values The distribution of sample means is the distribution that results when we find the means of all. The distribution of sample means. The expected value, the standard deviation and the. If \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from a \(n(\mu, \sigma^2)\) population, then the sample mean:. Let’s look at a simulation: It is. Distribution Of X Bar Values.
From www.slideserve.com
PPT Sampling Distributions PowerPoint Presentation, free download ID850396 Distribution Of X Bar Values The sample mean is a random variable; The expected value, the standard deviation and the. There are three things we need to know to fully describe a probability distribution of $\bar{x}$: If \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from a \(n(\mu, \sigma^2)\) population, then the sample mean:. As such it is written \(\bar{x}\),. Distribution Of X Bar Values.
From sixsigmadsi.com
What is X Bar in Statistics? Distribution Of X Bar Values The sample mean is a random variable; The distribution of sample means. The expected value, the standard deviation and the. It is a critical concept in. There are three things we need to know to fully describe a probability distribution of $\bar{x}$: As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. Let’s look at a. Distribution Of X Bar Values.
From www.cuemath.com
Frequency Distribution Definition, Facts & Examples Cuemath Distribution Of X Bar Values As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. Let’s look at a simulation: The sample mean is a random variable; There are three things we need to know to fully describe a probability distribution of $\bar{x}$: If \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from a \(n(\mu, \sigma^2)\). Distribution Of X Bar Values.
From www.scribbr.com
The Standard Normal Distribution Examples, Explanations, Uses Distribution Of X Bar Values The distribution of sample means is the distribution that results when we find the means of all. As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. Let’s look at a simulation: The sample mean is a random variable; The distribution of sample means. It is a critical concept in. The expected value, the standard deviation. Distribution Of X Bar Values.
From www.investopedia.com
The Normal Distribution Table Definition Distribution Of X Bar Values The expected value, the standard deviation and the. If \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from a \(n(\mu, \sigma^2)\) population, then the sample mean:. It is a critical concept in. As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. The sample mean is a random variable; Let’s look. Distribution Of X Bar Values.
From www.cuemath.com
Discrete Probability Distribution Examples, Definition, Types Distribution Of X Bar Values It is a critical concept in. The distribution of sample means is the distribution that results when we find the means of all. As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. There are three things we need to know to fully describe a probability distribution of $\bar{x}$: Let’s look at a simulation: If \(x_1,. Distribution Of X Bar Values.
From www.investopedia.com
The Normal Distribution Table Definition Distribution Of X Bar Values As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. If \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from a \(n(\mu, \sigma^2)\) population, then the sample mean:. Let’s look at a simulation: The expected value, the standard deviation and the. The sample mean is a random variable; The distribution of. Distribution Of X Bar Values.
From www.youtube.com
The Sampling Distribution of Xbar and the Central Limit Theorem YouTube Distribution Of X Bar Values As such it is written \(\bar{x}\), and \(\bar{x}\) stands for individual values it takes. The expected value, the standard deviation and the. Let’s look at a simulation: The distribution of sample means is the distribution that results when we find the means of all. The distribution of sample means. If \(x_1, x_2, \ldots, x_n\) are observations of a random sample. Distribution Of X Bar Values.