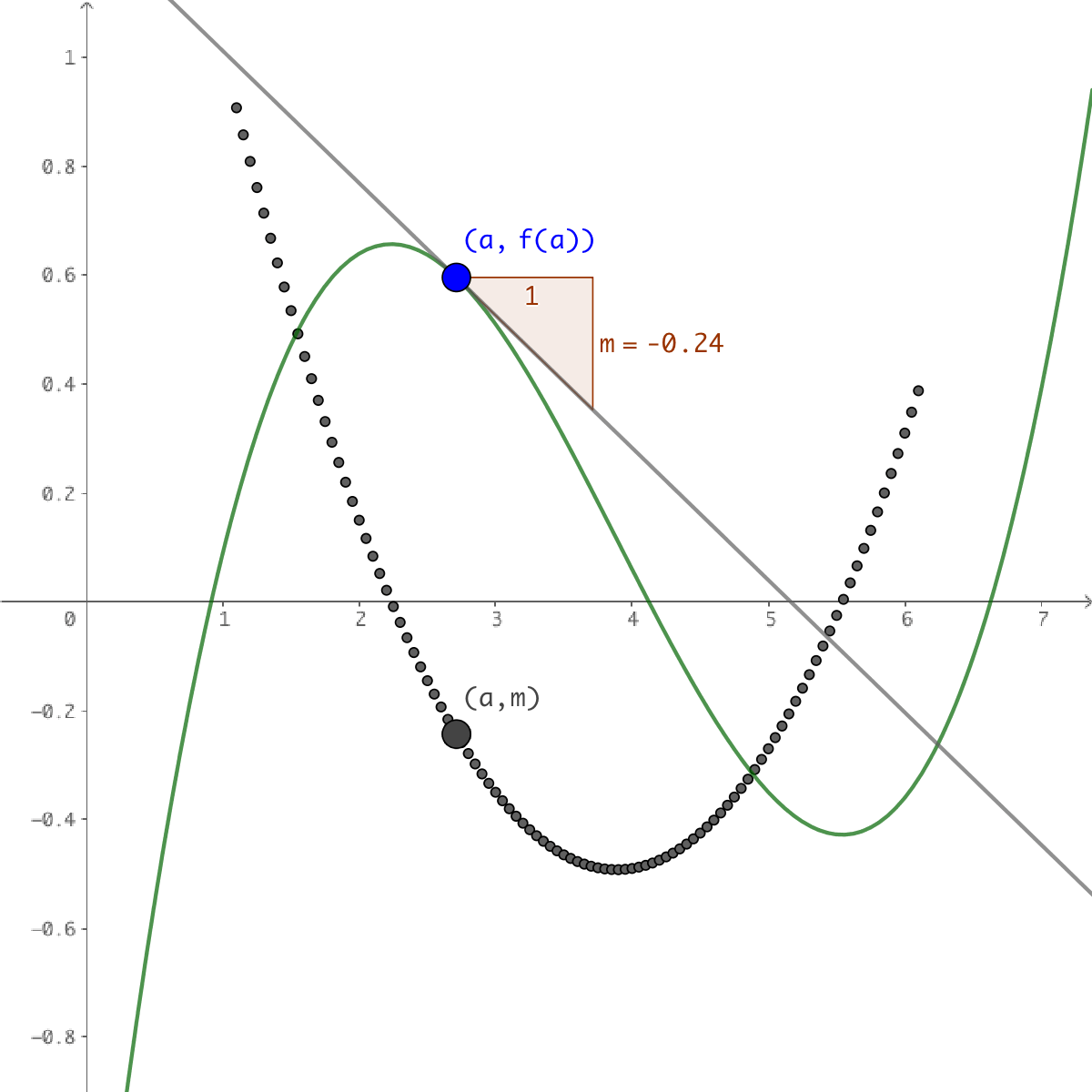
Derivatans Definition Cos X . We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. The proof begins by stating the definition of the derivative of a real function at a point. Can we prove them somehow? D dx sin (x) = cos (x) d dx cos (x) = −sin (x) d dx tan (x) = sec 2 (x) did they just drop out of the sky? The derivatives of sin x and cos x. In this case, it’s the derivative of cos (x) with respect to x,. The derivative of the sine function is the cosine and the derivative of the cosine function is the negative. The derivatives of sin x and cos x. The derivative of the sine function is the cosine and the derivative of the cosine function is the negative sine. The first steps towards computing the derivatives of \(\sin x, \cos x\) is to find their derivatives at \(x=0\text{.}\) the derivatives at general points. The three most useful derivatives in trigonometry are:
from www.malinc.se
D dx sin (x) = cos (x) d dx cos (x) = −sin (x) d dx tan (x) = sec 2 (x) did they just drop out of the sky? We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. The derivative of the sine function is the cosine and the derivative of the cosine function is the negative sine. The three most useful derivatives in trigonometry are: Can we prove them somehow? The proof begins by stating the definition of the derivative of a real function at a point. The derivatives of sin x and cos x. The first steps towards computing the derivatives of \(\sin x, \cos x\) is to find their derivatives at \(x=0\text{.}\) the derivatives at general points. The derivative of the sine function is the cosine and the derivative of the cosine function is the negative. In this case, it’s the derivative of cos (x) with respect to x,.
Analys Derivatans definition
Derivatans Definition Cos X The derivatives of sin x and cos x. The derivatives of sin x and cos x. In this case, it’s the derivative of cos (x) with respect to x,. The three most useful derivatives in trigonometry are: The derivative of the sine function is the cosine and the derivative of the cosine function is the negative. The proof begins by stating the definition of the derivative of a real function at a point. We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. The derivative of the sine function is the cosine and the derivative of the cosine function is the negative sine. The first steps towards computing the derivatives of \(\sin x, \cos x\) is to find their derivatives at \(x=0\text{.}\) the derivatives at general points. D dx sin (x) = cos (x) d dx cos (x) = −sin (x) d dx tan (x) = sec 2 (x) did they just drop out of the sky? The derivatives of sin x and cos x. Can we prove them somehow?
From slideplayer.com
Copyright © Cengage Learning. All rights reserved. ppt download Derivatans Definition Cos X We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. The proof begins by stating the definition of the derivative of a real function at a point. D dx sin (x) = cos (x) d dx cos (x) = −sin (x) d dx tan (x) = sec. Derivatans Definition Cos X.
From www.malinc.se
Analys Derivatans definition Derivatans Definition Cos X In this case, it’s the derivative of cos (x) with respect to x,. The derivatives of sin x and cos x. We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. The three most useful derivatives in trigonometry are: The first steps towards computing the derivatives of. Derivatans Definition Cos X.
From www.youtube.com
Definition of Derivative Part 2 (x^2/3 and cos(3x)) YouTube Derivatans Definition Cos X We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. The derivative of the sine function is the cosine and the derivative of the cosine function is the negative sine. The first steps towards computing the derivatives of \(\sin x, \cos x\) is to find their derivatives. Derivatans Definition Cos X.
From www.askmattrab.com
Derivative of trigonometric function sinx and Class Eleven Maths Derivatans Definition Cos X The proof begins by stating the definition of the derivative of a real function at a point. D dx sin (x) = cos (x) d dx cos (x) = −sin (x) d dx tan (x) = sec 2 (x) did they just drop out of the sky? We can find the derivatives of \(\sin x\) and \(\cos x\) by using. Derivatans Definition Cos X.
From www.youtube.com
What is the Derivative of cos2x cos 2x Derivative Derivative of cos(2x) YouTube Derivatans Definition Cos X The derivatives of sin x and cos x. The proof begins by stating the definition of the derivative of a real function at a point. The derivatives of sin x and cos x. The three most useful derivatives in trigonometry are: In this case, it’s the derivative of cos (x) with respect to x,. The first steps towards computing the. Derivatans Definition Cos X.
From theodorenewskelley.blogspot.com
Derivative of Cos X Derivatans Definition Cos X The three most useful derivatives in trigonometry are: The first steps towards computing the derivatives of \(\sin x, \cos x\) is to find their derivatives at \(x=0\text{.}\) the derivatives at general points. The derivative of the sine function is the cosine and the derivative of the cosine function is the negative sine. The proof begins by stating the definition of. Derivatans Definition Cos X.
From matematiklektion.weebly.com
Derivatans definition matematiklektion.se Derivatans Definition Cos X The three most useful derivatives in trigonometry are: The derivatives of sin x and cos x. The derivative of the sine function is the cosine and the derivative of the cosine function is the negative sine. We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. D. Derivatans Definition Cos X.
From www.youtube.com
Matematik 3 DERIVATANS DEFINITION (tydlig genomgång tror jag!) YouTube Derivatans Definition Cos X In this case, it’s the derivative of cos (x) with respect to x,. The derivative of the sine function is the cosine and the derivative of the cosine function is the negative. We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. The derivatives of sin x. Derivatans Definition Cos X.
From evgenii.com
Basic derivatives Derivatans Definition Cos X Can we prove them somehow? The proof begins by stating the definition of the derivative of a real function at a point. We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. In this case, it’s the derivative of cos (x) with respect to x,. The three. Derivatans Definition Cos X.
From www.cuemath.com
Derivatives Calculus, Meaning, Interpretation Derivatans Definition Cos X The derivative of the sine function is the cosine and the derivative of the cosine function is the negative. The derivatives of sin x and cos x. D dx sin (x) = cos (x) d dx cos (x) = −sin (x) d dx tan (x) = sec 2 (x) did they just drop out of the sky? The derivatives of. Derivatans Definition Cos X.
From www.malinc.se
Analys Derivatans definition Derivatans Definition Cos X Can we prove them somehow? The proof begins by stating the definition of the derivative of a real function at a point. The derivative of the sine function is the cosine and the derivative of the cosine function is the negative sine. We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and. Derivatans Definition Cos X.
From www.pluggakuten.se
Derivatans definition (Matematik/Matte 5/Differentialekvationer) Pluggakuten Derivatans Definition Cos X The three most useful derivatives in trigonometry are: Can we prove them somehow? The proof begins by stating the definition of the derivative of a real function at a point. The derivatives of sin x and cos x. The first steps towards computing the derivatives of \(\sin x, \cos x\) is to find their derivatives at \(x=0\text{.}\) the derivatives at. Derivatans Definition Cos X.
From www.pluggakuten.se
derivatans definition (Matematik/Matte 3/Derivata) Pluggakuten Derivatans Definition Cos X The derivative of the sine function is the cosine and the derivative of the cosine function is the negative sine. The derivatives of sin x and cos x. The derivatives of sin x and cos x. The proof begins by stating the definition of the derivative of a real function at a point. The first steps towards computing the derivatives. Derivatans Definition Cos X.
From derivativeit.com
The Derivative of Cos DerivativeIt Derivatans Definition Cos X The derivative of the sine function is the cosine and the derivative of the cosine function is the negative. The derivatives of sin x and cos x. In this case, it’s the derivative of cos (x) with respect to x,. Can we prove them somehow? The three most useful derivatives in trigonometry are: The derivatives of sin x and cos. Derivatans Definition Cos X.
From www.youtube.com
Exempel på derivatans definition YouTube Derivatans Definition Cos X The proof begins by stating the definition of the derivative of a real function at a point. The three most useful derivatives in trigonometry are: The derivative of the sine function is the cosine and the derivative of the cosine function is the negative sine. D dx sin (x) = cos (x) d dx cos (x) = −sin (x) d. Derivatans Definition Cos X.
From epsilonify.com
Derivative of cos(x) using First Principle of Derivatives [FULL PROOF] Derivatans Definition Cos X We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. D dx sin (x) = cos (x) d dx cos (x) = −sin (x) d dx tan (x) = sec 2 (x) did they just drop out of the sky? The three most useful derivatives in trigonometry. Derivatans Definition Cos X.
From www.yawin.in
Find the derivatives of cos x from the first principle Yawin Derivatans Definition Cos X The derivatives of sin x and cos x. The derivatives of sin x and cos x. We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. The derivative of the sine function is the cosine and the derivative of the cosine function is the negative. Can we. Derivatans Definition Cos X.
From zakruti.com
Derivatives of sin(x) and cos(x) Derivative rules AP Calculus AB Derivatans Definition Cos X The derivative of the sine function is the cosine and the derivative of the cosine function is the negative. The first steps towards computing the derivatives of \(\sin x, \cos x\) is to find their derivatives at \(x=0\text{.}\) the derivatives at general points. The derivatives of sin x and cos x. We can find the derivatives of \(\sin x\) and. Derivatans Definition Cos X.
From www.slideserve.com
PPT Derivatives of Sine and Cosine PowerPoint Presentation, free download ID2597914 Derivatans Definition Cos X In this case, it’s the derivative of cos (x) with respect to x,. The three most useful derivatives in trigonometry are: D dx sin (x) = cos (x) d dx cos (x) = −sin (x) d dx tan (x) = sec 2 (x) did they just drop out of the sky? The derivative of the sine function is the cosine. Derivatans Definition Cos X.
From www.malinc.se
Analys Derivatans definition Derivatans Definition Cos X Can we prove them somehow? The proof begins by stating the definition of the derivative of a real function at a point. The derivatives of sin x and cos x. D dx sin (x) = cos (x) d dx cos (x) = −sin (x) d dx tan (x) = sec 2 (x) did they just drop out of the sky?. Derivatans Definition Cos X.
From www.pluggakuten.se
Derivatans definition (Matematik/Matte 4/Derivata) Pluggakuten Derivatans Definition Cos X The first steps towards computing the derivatives of \(\sin x, \cos x\) is to find their derivatives at \(x=0\text{.}\) the derivatives at general points. We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. D dx sin (x) = cos (x) d dx cos (x) = −sin. Derivatans Definition Cos X.
From www.teachoo.com
Find the Derivative of cos1 x (Cos inverse x) Teachoo Derivatans Definition Cos X In this case, it’s the derivative of cos (x) with respect to x,. We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. The derivative of the sine function is the cosine and the derivative of the cosine function is the negative. The derivative of the sine. Derivatans Definition Cos X.
From www.teachoo.com
Example 27 Find derivative of f(x) = tan1 x Class 12 Derivatans Definition Cos X The derivative of the sine function is the cosine and the derivative of the cosine function is the negative. The derivatives of sin x and cos x. Can we prove them somehow? The first steps towards computing the derivatives of \(\sin x, \cos x\) is to find their derivatives at \(x=0\text{.}\) the derivatives at general points. The proof begins by. Derivatans Definition Cos X.
From apaftgee.blogspot.com
Differentiation Of Cos Cube X / What Is The Derivative Of Cos 3 X Socratic Derivatives of cos Derivatans Definition Cos X The first steps towards computing the derivatives of \(\sin x, \cos x\) is to find their derivatives at \(x=0\text{.}\) the derivatives at general points. We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. The three most useful derivatives in trigonometry are: The derivatives of sin x. Derivatans Definition Cos X.
From www.youtube.com
Cos(x)= Sin(x). Proof by definition of derivative Calculus Derivatives proof YouTube Derivatans Definition Cos X The derivative of the sine function is the cosine and the derivative of the cosine function is the negative. D dx sin (x) = cos (x) d dx cos (x) = −sin (x) d dx tan (x) = sec 2 (x) did they just drop out of the sky? The derivatives of sin x and cos x. The first steps. Derivatans Definition Cos X.
From www.youtube.com
Proof that the Derivative of cos(x) is sin(x) using the Limit Definition of the Derivative Derivatans Definition Cos X The derivative of the sine function is the cosine and the derivative of the cosine function is the negative sine. The derivative of the sine function is the cosine and the derivative of the cosine function is the negative. Can we prove them somehow? The first steps towards computing the derivatives of \(\sin x, \cos x\) is to find their. Derivatans Definition Cos X.
From www.cuemath.com
Derivatives Calculus, Meaning, Interpretation Derivatans Definition Cos X The derivative of the sine function is the cosine and the derivative of the cosine function is the negative sine. The derivatives of sin x and cos x. D dx sin (x) = cos (x) d dx cos (x) = −sin (x) d dx tan (x) = sec 2 (x) did they just drop out of the sky? The three. Derivatans Definition Cos X.
From www.teachoo.com
Ex 12.2, 10 Find derivative of cos x from first principle Teachoo Derivatans Definition Cos X We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. The derivatives of sin x and cos x. In this case, it’s the derivative of cos (x) with respect to x,. D dx sin (x) = cos (x) d dx cos (x) = −sin (x) d dx. Derivatans Definition Cos X.
From www.youtube.com
The PROOF that the Derivative of sin(x) is cos(x)!!! Limit Definition of Derivatives YouTube Derivatans Definition Cos X The proof begins by stating the definition of the derivative of a real function at a point. Can we prove them somehow? The derivative of the sine function is the cosine and the derivative of the cosine function is the negative. The first steps towards computing the derivatives of \(\sin x, \cos x\) is to find their derivatives at \(x=0\text{.}\). Derivatans Definition Cos X.
From kunduz.com
Differentiation of Trigonometric Functions Kunduz Derivatans Definition Cos X We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. In this case, it’s the derivative of cos (x) with respect to x,. D dx sin (x) = cos (x) d dx cos (x) = −sin (x) d dx tan (x) = sec 2 (x) did they. Derivatans Definition Cos X.
From www.youtube.com
Proof of the derivatives of sin(x) and cos(x) using the limit definition of a derivative by Derivatans Definition Cos X The three most useful derivatives in trigonometry are: The derivative of the sine function is the cosine and the derivative of the cosine function is the negative sine. The derivative of the sine function is the cosine and the derivative of the cosine function is the negative. In this case, it’s the derivative of cos (x) with respect to x,.. Derivatans Definition Cos X.
From declanqiarroyo.blogspot.com
Derivative of Cos X DeclanqiArroyo Derivatans Definition Cos X We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. D dx sin (x) = cos (x) d dx cos (x) = −sin (x) d dx tan (x) = sec 2 (x) did they just drop out of the sky? The three most useful derivatives in trigonometry. Derivatans Definition Cos X.
From www.teachoo.com
Ex 12.2, 10 Find derivative of cos x from first principle Teachoo Derivatans Definition Cos X The derivatives of sin x and cos x. D dx sin (x) = cos (x) d dx cos (x) = −sin (x) d dx tan (x) = sec 2 (x) did they just drop out of the sky? We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found. Derivatans Definition Cos X.
From mavink.com
Matrix Derivative Cheat Sheet Derivatans Definition Cos X Can we prove them somehow? The derivatives of sin x and cos x. The derivatives of sin x and cos x. The first steps towards computing the derivatives of \(\sin x, \cos x\) is to find their derivatives at \(x=0\text{.}\) the derivatives at general points. The derivative of the sine function is the cosine and the derivative of the cosine. Derivatans Definition Cos X.
From www.teachoo.com
Example 16 Compute derivative of sin x Chapter 13 Class 11 Examp Derivatans Definition Cos X In this case, it’s the derivative of cos (x) with respect to x,. The three most useful derivatives in trigonometry are: The derivatives of sin x and cos x. The derivative of the sine function is the cosine and the derivative of the cosine function is the negative. The proof begins by stating the definition of the derivative of a. Derivatans Definition Cos X.