Euler's Formula Questions . Euler's formula for complex analysis: For complex numbers \( x \), euler's formula says. Euler’s formula is very simple but also very important in geometrical mathematics. A complete guide on the famous euler's formula for complex numbers, along with its interpretations, examples, derivations and numerous applications. E ix = cos x + isin x. In complex analysis, euler's formula provides a fundamental bridge between the exponential function and the trigonometric functions. The following are two different euler's formulas used in different contexts. Plus the number of vertices (corner points) minus the. It deals with the shapes called polyhedron. For any polyhedron that doesn't intersect itself, the. Euler’s (pronounced ‘oilers’) formula connects complex exponentials, polar coordinates, and sines and cosines. It turns messy trig identities into tidy rules for exponentials.
from www.numerade.com
In complex analysis, euler's formula provides a fundamental bridge between the exponential function and the trigonometric functions. The following are two different euler's formulas used in different contexts. E ix = cos x + isin x. For any polyhedron that doesn't intersect itself, the. For complex numbers \( x \), euler's formula says. Euler’s formula is very simple but also very important in geometrical mathematics. Plus the number of vertices (corner points) minus the. It turns messy trig identities into tidy rules for exponentials. Euler's formula for complex analysis: It deals with the shapes called polyhedron.
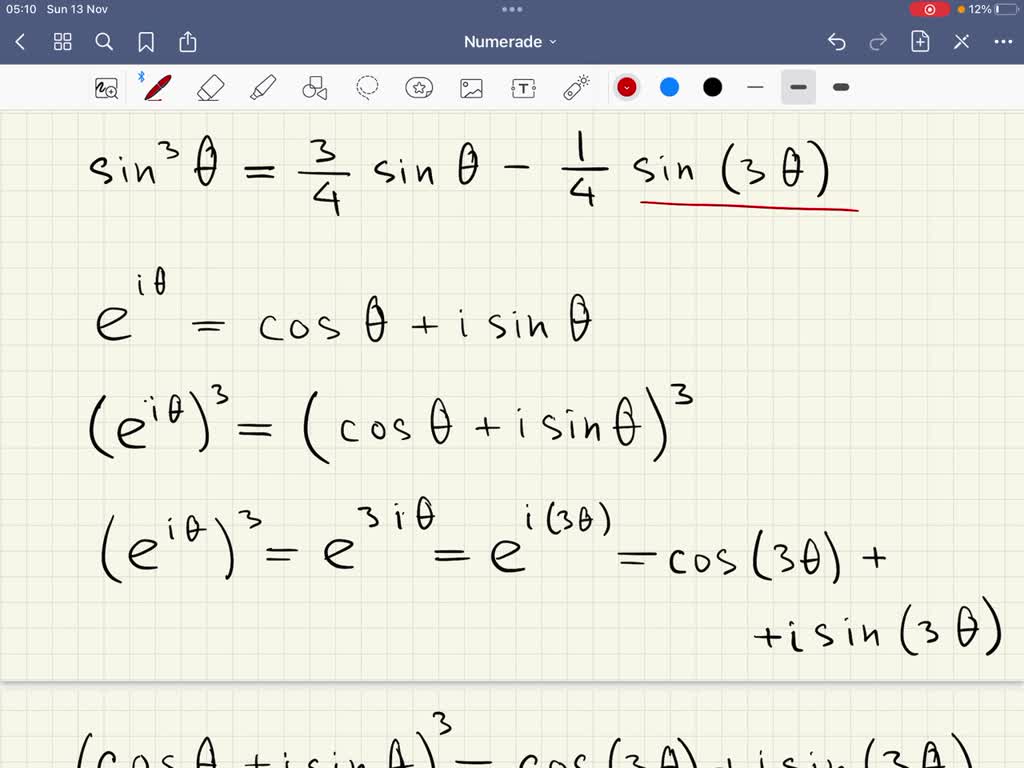
SOLVED Use Euler's formula to prove the identity sin ^3θ=(3)/(4)sinθ(1)/(4)sin 3 θ
Euler's Formula Questions Euler’s formula is very simple but also very important in geometrical mathematics. Euler’s (pronounced ‘oilers’) formula connects complex exponentials, polar coordinates, and sines and cosines. Plus the number of vertices (corner points) minus the. Euler's formula for complex analysis: In complex analysis, euler's formula provides a fundamental bridge between the exponential function and the trigonometric functions. E ix = cos x + isin x. A complete guide on the famous euler's formula for complex numbers, along with its interpretations, examples, derivations and numerous applications. For complex numbers \( x \), euler's formula says. Euler’s formula is very simple but also very important in geometrical mathematics. It turns messy trig identities into tidy rules for exponentials. The following are two different euler's formulas used in different contexts. For any polyhedron that doesn't intersect itself, the. It deals with the shapes called polyhedron.
From www.chegg.com
Solved Question 1 Using Euler's formula a) Evaluate ejx b) Euler's Formula Questions It deals with the shapes called polyhedron. Euler’s (pronounced ‘oilers’) formula connects complex exponentials, polar coordinates, and sines and cosines. In complex analysis, euler's formula provides a fundamental bridge between the exponential function and the trigonometric functions. Euler's formula for complex analysis: Plus the number of vertices (corner points) minus the. A complete guide on the famous euler's formula for. Euler's Formula Questions.
From byjusexamprep.com
Euler's Equation of Motion Assumptions, Derivation [GATE Notes] Euler's Formula Questions Euler’s formula is very simple but also very important in geometrical mathematics. The following are two different euler's formulas used in different contexts. For complex numbers \( x \), euler's formula says. E ix = cos x + isin x. In complex analysis, euler's formula provides a fundamental bridge between the exponential function and the trigonometric functions. Plus the number. Euler's Formula Questions.
From www.chegg.com
Solved Using Euler's formula, e jtheta = COS(theta) j Euler's Formula Questions It deals with the shapes called polyhedron. In complex analysis, euler's formula provides a fundamental bridge between the exponential function and the trigonometric functions. For complex numbers \( x \), euler's formula says. E ix = cos x + isin x. It turns messy trig identities into tidy rules for exponentials. Euler's formula for complex analysis: Euler’s formula is very. Euler's Formula Questions.
From www.chegg.com
Solved Exercise 4 Euler [25 pts]. The Euler equation is Euler's Formula Questions Plus the number of vertices (corner points) minus the. Euler’s (pronounced ‘oilers’) formula connects complex exponentials, polar coordinates, and sines and cosines. It deals with the shapes called polyhedron. Euler’s formula is very simple but also very important in geometrical mathematics. For any polyhedron that doesn't intersect itself, the. In complex analysis, euler's formula provides a fundamental bridge between the. Euler's Formula Questions.
From www.teachoo.com
[Solid Shapes Class 8] Verify Euler’s formula for these solids Euler's Formula Questions Euler's formula for complex analysis: Euler’s formula is very simple but also very important in geometrical mathematics. The following are two different euler's formulas used in different contexts. Euler’s (pronounced ‘oilers’) formula connects complex exponentials, polar coordinates, and sines and cosines. It deals with the shapes called polyhedron. In complex analysis, euler's formula provides a fundamental bridge between the exponential. Euler's Formula Questions.
From www.chegg.com
Solved Use Euler's formula for the complex exponential to Euler's Formula Questions The following are two different euler's formulas used in different contexts. In complex analysis, euler's formula provides a fundamental bridge between the exponential function and the trigonometric functions. For complex numbers \( x \), euler's formula says. Plus the number of vertices (corner points) minus the. It deals with the shapes called polyhedron. Euler’s (pronounced ‘oilers’) formula connects complex exponentials,. Euler's Formula Questions.
From www.teachoo.com
[Visualing Solid Shapes] Using Euler’s formula find the unknown Euler's Formula Questions For any polyhedron that doesn't intersect itself, the. It turns messy trig identities into tidy rules for exponentials. E ix = cos x + isin x. For complex numbers \( x \), euler's formula says. Euler’s (pronounced ‘oilers’) formula connects complex exponentials, polar coordinates, and sines and cosines. The following are two different euler's formulas used in different contexts. It. Euler's Formula Questions.
From www.livescience.com
Euler’s Identity 'The Most Beautiful Equation' Live Science Euler's Formula Questions Euler’s formula is very simple but also very important in geometrical mathematics. Euler’s (pronounced ‘oilers’) formula connects complex exponentials, polar coordinates, and sines and cosines. The following are two different euler's formulas used in different contexts. It deals with the shapes called polyhedron. Euler's formula for complex analysis: In complex analysis, euler's formula provides a fundamental bridge between the exponential. Euler's Formula Questions.
From askfilo.com
Using Euler's formula, find V, if E=30, F=12. empt any four subquestions.. Euler's Formula Questions Plus the number of vertices (corner points) minus the. For any polyhedron that doesn't intersect itself, the. Euler's formula for complex analysis: In complex analysis, euler's formula provides a fundamental bridge between the exponential function and the trigonometric functions. A complete guide on the famous euler's formula for complex numbers, along with its interpretations, examples, derivations and numerous applications. For. Euler's Formula Questions.
From www.home-tution.com
Euler's Formula Definition, Use, Facts & Examples Euler's Formula Questions For complex numbers \( x \), euler's formula says. For any polyhedron that doesn't intersect itself, the. A complete guide on the famous euler's formula for complex numbers, along with its interpretations, examples, derivations and numerous applications. It turns messy trig identities into tidy rules for exponentials. In complex analysis, euler's formula provides a fundamental bridge between the exponential function. Euler's Formula Questions.
From www.alamy.com
Euler’s formula explained on a chalkboard Stock Photo Alamy Euler's Formula Questions The following are two different euler's formulas used in different contexts. E ix = cos x + isin x. For any polyhedron that doesn't intersect itself, the. It deals with the shapes called polyhedron. For complex numbers \( x \), euler's formula says. Plus the number of vertices (corner points) minus the. Euler’s formula is very simple but also very. Euler's Formula Questions.
From www.vedantu.com
Euler’s Theorem Learn and Solve Questions Euler's Formula Questions A complete guide on the famous euler's formula for complex numbers, along with its interpretations, examples, derivations and numerous applications. It turns messy trig identities into tidy rules for exponentials. E ix = cos x + isin x. For complex numbers \( x \), euler's formula says. The following are two different euler's formulas used in different contexts. Euler’s (pronounced. Euler's Formula Questions.
From www.numerade.com
⏩SOLVEDFind a first integrat of the Euler equation to make… Numerade Euler's Formula Questions Euler’s formula is very simple but also very important in geometrical mathematics. The following are two different euler's formulas used in different contexts. E ix = cos x + isin x. Euler’s (pronounced ‘oilers’) formula connects complex exponentials, polar coordinates, and sines and cosines. Plus the number of vertices (corner points) minus the. It turns messy trig identities into tidy. Euler's Formula Questions.
From www.gauthmath.com
Solved Question 3 (1 point) Use Euler's Formula to find the missing number. Faces 25 Vertices Euler's Formula Questions E ix = cos x + isin x. It turns messy trig identities into tidy rules for exponentials. Plus the number of vertices (corner points) minus the. The following are two different euler's formulas used in different contexts. Euler's formula for complex analysis: Euler’s (pronounced ‘oilers’) formula connects complex exponentials, polar coordinates, and sines and cosines. It deals with the. Euler's Formula Questions.
From www.youtube.com
Euler's Formula, Simplifying complex numbers in Exponential Forms Advanced Engineering Euler's Formula Questions The following are two different euler's formulas used in different contexts. Euler’s formula is very simple but also very important in geometrical mathematics. In complex analysis, euler's formula provides a fundamental bridge between the exponential function and the trigonometric functions. It turns messy trig identities into tidy rules for exponentials. Euler’s (pronounced ‘oilers’) formula connects complex exponentials, polar coordinates, and. Euler's Formula Questions.
From www.nagwa.com
Question Video Using Euler’s Formula to Derive Formulas for Trigonometric Functions Nagwa Euler's Formula Questions In complex analysis, euler's formula provides a fundamental bridge between the exponential function and the trigonometric functions. For complex numbers \( x \), euler's formula says. Plus the number of vertices (corner points) minus the. The following are two different euler's formulas used in different contexts. It deals with the shapes called polyhedron. It turns messy trig identities into tidy. Euler's Formula Questions.
From www.grc.nasa.gov
Euler Equations Euler's Formula Questions Euler's formula for complex analysis: It deals with the shapes called polyhedron. For any polyhedron that doesn't intersect itself, the. For complex numbers \( x \), euler's formula says. A complete guide on the famous euler's formula for complex numbers, along with its interpretations, examples, derivations and numerous applications. Euler’s (pronounced ‘oilers’) formula connects complex exponentials, polar coordinates, and sines. Euler's Formula Questions.
From www.coursehero.com
[Solved] pls show step by step. Question 7. Consider the Euler equation... Course Hero Euler's Formula Questions Euler's formula for complex analysis: In complex analysis, euler's formula provides a fundamental bridge between the exponential function and the trigonometric functions. For any polyhedron that doesn't intersect itself, the. Euler’s formula is very simple but also very important in geometrical mathematics. It deals with the shapes called polyhedron. E ix = cos x + isin x. Plus the number. Euler's Formula Questions.
From www.coursehero.com
[Solved] Apply Euler's method to the following equation with initial... Course Hero Euler's Formula Questions It deals with the shapes called polyhedron. It turns messy trig identities into tidy rules for exponentials. For any polyhedron that doesn't intersect itself, the. The following are two different euler's formulas used in different contexts. Plus the number of vertices (corner points) minus the. Euler’s (pronounced ‘oilers’) formula connects complex exponentials, polar coordinates, and sines and cosines. E ix. Euler's Formula Questions.
From www.youtube.com
How To Apply Euler's Theorem Of Homogeneous Functions And Its Deductions? Solved Example 3 YouTube Euler's Formula Questions E ix = cos x + isin x. Euler's formula for complex analysis: Euler’s (pronounced ‘oilers’) formula connects complex exponentials, polar coordinates, and sines and cosines. In complex analysis, euler's formula provides a fundamental bridge between the exponential function and the trigonometric functions. The following are two different euler's formulas used in different contexts. For any polyhedron that doesn't intersect. Euler's Formula Questions.
From wizedu.com
Derive the expression for the Euler’s formula (the critical load) for pinended columns. WizEdu Euler's Formula Questions Plus the number of vertices (corner points) minus the. Euler’s (pronounced ‘oilers’) formula connects complex exponentials, polar coordinates, and sines and cosines. Euler's formula for complex analysis: For any polyhedron that doesn't intersect itself, the. E ix = cos x + isin x. A complete guide on the famous euler's formula for complex numbers, along with its interpretations, examples, derivations. Euler's Formula Questions.
From www.slideserve.com
PPT Euler’s Equation PowerPoint Presentation, free download ID324004 Euler's Formula Questions In complex analysis, euler's formula provides a fundamental bridge between the exponential function and the trigonometric functions. It deals with the shapes called polyhedron. Euler’s (pronounced ‘oilers’) formula connects complex exponentials, polar coordinates, and sines and cosines. Plus the number of vertices (corner points) minus the. For complex numbers \( x \), euler's formula says. Euler’s formula is very simple. Euler's Formula Questions.
From www.cuemath.com
Euler's Formula Complex Numbers, Polyhedra, Euler's Identity Euler's Formula Questions In complex analysis, euler's formula provides a fundamental bridge between the exponential function and the trigonometric functions. It deals with the shapes called polyhedron. For any polyhedron that doesn't intersect itself, the. For complex numbers \( x \), euler's formula says. E ix = cos x + isin x. A complete guide on the famous euler's formula for complex numbers,. Euler's Formula Questions.
From www.youtube.com
Euler's Theorem Example Euler's Theorem Question Euler's Theorem Problems Deduction of Euler's Formula Questions Euler's formula for complex analysis: For any polyhedron that doesn't intersect itself, the. Euler’s (pronounced ‘oilers’) formula connects complex exponentials, polar coordinates, and sines and cosines. In complex analysis, euler's formula provides a fundamental bridge between the exponential function and the trigonometric functions. The following are two different euler's formulas used in different contexts. E ix = cos x +. Euler's Formula Questions.
From www.youtube.com
Euler's Theorem questions B.Sc. Maths YouTube Euler's Formula Questions Plus the number of vertices (corner points) minus the. Euler's formula for complex analysis: For any polyhedron that doesn't intersect itself, the. E ix = cos x + isin x. It turns messy trig identities into tidy rules for exponentials. It deals with the shapes called polyhedron. Euler’s (pronounced ‘oilers’) formula connects complex exponentials, polar coordinates, and sines and cosines.. Euler's Formula Questions.
From www.teachoo.com
[Visualing Solid Shapes] Using Euler’s formula find the unknown Euler's Formula Questions It turns messy trig identities into tidy rules for exponentials. E ix = cos x + isin x. Euler’s formula is very simple but also very important in geometrical mathematics. In complex analysis, euler's formula provides a fundamental bridge between the exponential function and the trigonometric functions. It deals with the shapes called polyhedron. For any polyhedron that doesn't intersect. Euler's Formula Questions.
From www.transtutors.com
(Solved) 1. Use The Euler's Formula To Show That I. Cos(X) = Cos(X) II.... (1 Answer Euler's Formula Questions A complete guide on the famous euler's formula for complex numbers, along with its interpretations, examples, derivations and numerous applications. It deals with the shapes called polyhedron. Euler’s (pronounced ‘oilers’) formula connects complex exponentials, polar coordinates, and sines and cosines. For any polyhedron that doesn't intersect itself, the. In complex analysis, euler's formula provides a fundamental bridge between the exponential. Euler's Formula Questions.
From www.chegg.com
Solved For an Euler's equation, with constant coefficients, Euler's Formula Questions The following are two different euler's formulas used in different contexts. For any polyhedron that doesn't intersect itself, the. In complex analysis, euler's formula provides a fundamental bridge between the exponential function and the trigonometric functions. Euler’s (pronounced ‘oilers’) formula connects complex exponentials, polar coordinates, and sines and cosines. Euler’s formula is very simple but also very important in geometrical. Euler's Formula Questions.
From www.youtube.com
Euler’s formula, Chapter 10, Visualising Solid Shapes, Class 8, Maths YouTube Euler's Formula Questions In complex analysis, euler's formula provides a fundamental bridge between the exponential function and the trigonometric functions. It turns messy trig identities into tidy rules for exponentials. For any polyhedron that doesn't intersect itself, the. E ix = cos x + isin x. The following are two different euler's formulas used in different contexts. Euler's formula for complex analysis: Euler’s. Euler's Formula Questions.
From www.youtube.com
Euler's formula YouTube Euler's Formula Questions Euler’s (pronounced ‘oilers’) formula connects complex exponentials, polar coordinates, and sines and cosines. In complex analysis, euler's formula provides a fundamental bridge between the exponential function and the trigonometric functions. For any polyhedron that doesn't intersect itself, the. Euler's formula for complex analysis: E ix = cos x + isin x. It turns messy trig identities into tidy rules for. Euler's Formula Questions.
From www.britannica.com
Euler’s formula Definition & Facts Britannica Euler's Formula Questions A complete guide on the famous euler's formula for complex numbers, along with its interpretations, examples, derivations and numerous applications. The following are two different euler's formulas used in different contexts. Euler’s (pronounced ‘oilers’) formula connects complex exponentials, polar coordinates, and sines and cosines. For complex numbers \( x \), euler's formula says. Plus the number of vertices (corner points). Euler's Formula Questions.
From www.home-tution.com
Euler's Formula Definition, Use, Facts & Examples Euler's Formula Questions Euler’s (pronounced ‘oilers’) formula connects complex exponentials, polar coordinates, and sines and cosines. Euler’s formula is very simple but also very important in geometrical mathematics. It turns messy trig identities into tidy rules for exponentials. In complex analysis, euler's formula provides a fundamental bridge between the exponential function and the trigonometric functions. Euler's formula for complex analysis: E ix =. Euler's Formula Questions.
From www.chegg.com
Solved Euler's formula (v e + f = 2) holds for all Euler's Formula Questions For any polyhedron that doesn't intersect itself, the. A complete guide on the famous euler's formula for complex numbers, along with its interpretations, examples, derivations and numerous applications. It deals with the shapes called polyhedron. It turns messy trig identities into tidy rules for exponentials. The following are two different euler's formulas used in different contexts. In complex analysis, euler's. Euler's Formula Questions.
From andymath.com
Euler's Formula Euler's Formula Questions It turns messy trig identities into tidy rules for exponentials. Euler's formula for complex analysis: E ix = cos x + isin x. For complex numbers \( x \), euler's formula says. A complete guide on the famous euler's formula for complex numbers, along with its interpretations, examples, derivations and numerous applications. Plus the number of vertices (corner points) minus. Euler's Formula Questions.
From www.numerade.com
SOLVED Use Euler's formula to prove the identity sin ^3θ=(3)/(4)sinθ(1)/(4)sin 3 θ Euler's Formula Questions Euler’s (pronounced ‘oilers’) formula connects complex exponentials, polar coordinates, and sines and cosines. It deals with the shapes called polyhedron. E ix = cos x + isin x. In complex analysis, euler's formula provides a fundamental bridge between the exponential function and the trigonometric functions. Euler's formula for complex analysis: Plus the number of vertices (corner points) minus the. The. Euler's Formula Questions.