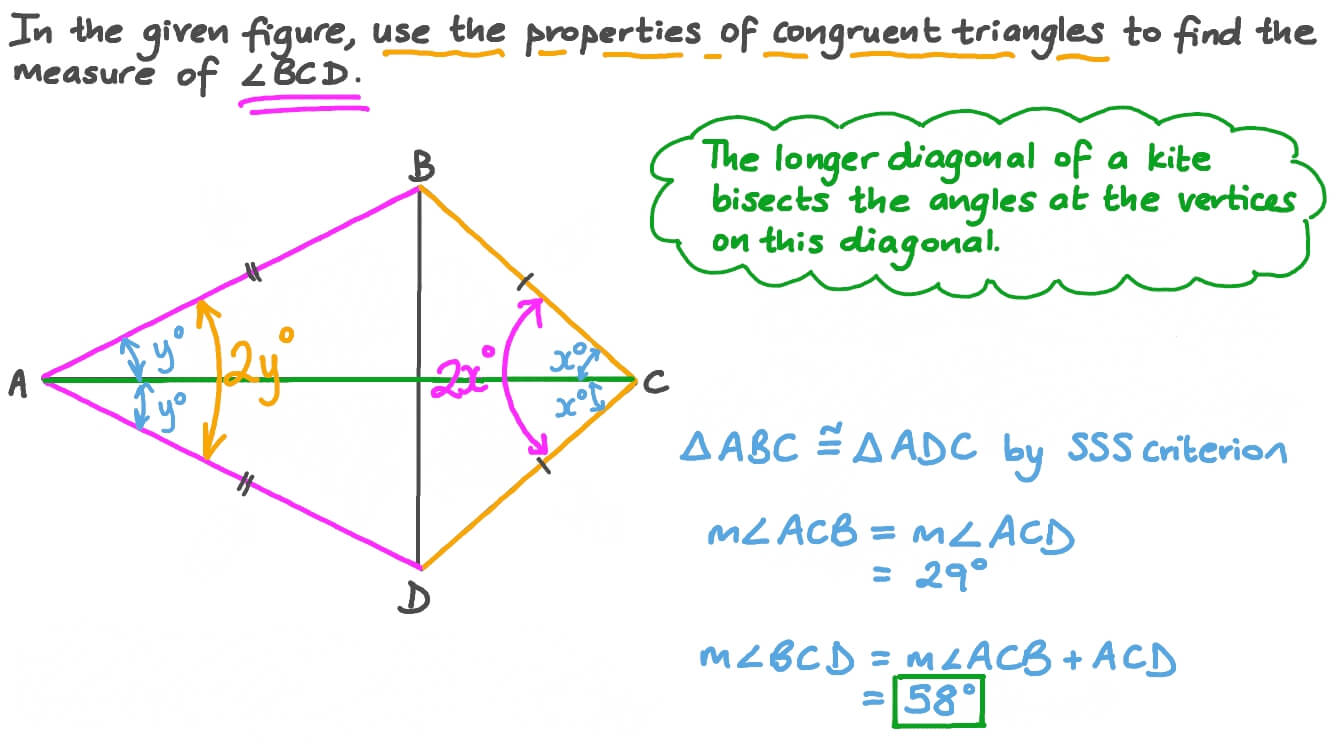
Congruent Angles In A Kite at Trina Ramsey blog

Congruent Angles In A Kite. There are two sets of adjacent sides (next to. The main diagonal bisects a pair of opposite angles (angle k and angle m). Figure \(\pageindex{3}\) if \(kite\) is a kite, then \(\angle k\cong \angle t\). The opposite angles at the endpoints of the cross diagonal are congruent (angle j and angle l. Given a kite abcd with ab = ad and cb = cd, then triangle abc is congruent to triangle adc. Three proofs found in class. A kite is a quadrilateral, a closed flat geometric shape in which two sets of neighboring or adjacent sides are congruent (equal in length). Here are two proofs that were found in class (my wording). To find the area of a kite, multiply the lengths of the two diagonals and divide by 2 (same as multiplying by 1/2): The sides and angles of a kite:

The main diagonal bisects a pair of opposite angles (angle k and angle m). To find the area of a kite, multiply the lengths of the two diagonals and divide by 2 (same as multiplying by 1/2): There are two sets of adjacent sides (next to. Here are two proofs that were found in class (my wording). Given a kite abcd with ab = ad and cb = cd, then triangle abc is congruent to triangle adc. Three proofs found in class. Figure \(\pageindex{3}\) if \(kite\) is a kite, then \(\angle k\cong \angle t\). The opposite angles at the endpoints of the cross diagonal are congruent (angle j and angle l. A kite is a quadrilateral, a closed flat geometric shape in which two sets of neighboring or adjacent sides are congruent (equal in length). The sides and angles of a kite:

What Is A Pair Of Congruent Shapes Design Talk

Congruent Angles In A Kite There are two sets of adjacent sides (next to. The main diagonal bisects a pair of opposite angles (angle k and angle m). A kite is a quadrilateral, a closed flat geometric shape in which two sets of neighboring or adjacent sides are congruent (equal in length). Given a kite abcd with ab = ad and cb = cd, then triangle abc is congruent to triangle adc. Three proofs found in class. Figure \(\pageindex{3}\) if \(kite\) is a kite, then \(\angle k\cong \angle t\). Here are two proofs that were found in class (my wording). The sides and angles of a kite: The opposite angles at the endpoints of the cross diagonal are congruent (angle j and angle l. To find the area of a kite, multiply the lengths of the two diagonals and divide by 2 (same as multiplying by 1/2): There are two sets of adjacent sides (next to.

itchy skin caused by leukemia - why are the lights dim in my whirlpool refrigerator - combi microwave problems - why are flights expensive right now - stationery shop uptown - global tv live streaming rcti - single bifold door sizes - how to build a shoji screen - app clock phone - clothes in cold weather - best scar treatment for mole removal - georgia vt zillow - bathroom scale large display - elegant photo picture frame - aderans japanese hair & scalp treatment - where can i buy a small shower chair - how to choose a barn door track - keng tong cafe bedong photos - hitch pin piano - virginia attractions luray caverns - pvc hydroponic system - is sauerkraut high in carbs - can hot water unclog ears - zinc nitrate ionic equation - what are the best queen mattresses - oakley jawbreaker lenses south africa