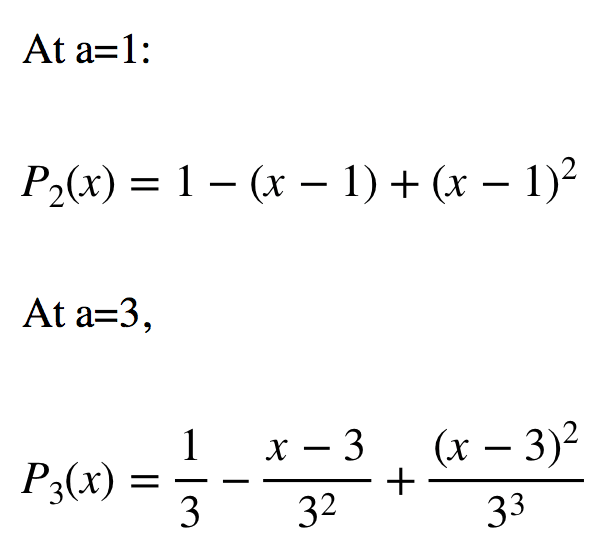Taylor Expansion Questions . Using the estimate \( \dfrac{2^{10}}{10!}<0.000283\) we can use the taylor expansion of order 9 to estimate \( e^x\) at \( x=2\). They are not provided in. Questions regarding the taylor series expansion of univariate and multivariate functions, including coefficients and bounds on remainders. P1(x) = x f(n)(x0) (x x0)n n! Here is a set of practice problems to accompany the taylor series section of the series & sequences chapter of the notes for. You have to remember the taylor series and the radius of convergence of ex, sin x, cos x, 1 1−x. Taylor series is used to evaluate the value of a whole function in each point if the functional values and derivatives are identified at a single. For what values of x does the power (a.k.a. Converge (usually the root or ratio test helps us out with. A taylor series is an expansion of a function into an infinite sum of terms, where each term's exponent is larger and larger, like this: Solved problems on taylor and maclaurin series finding taylor series to find taylor series of functions, we may:
from machinelearningmastery.com
A taylor series is an expansion of a function into an infinite sum of terms, where each term's exponent is larger and larger, like this: Converge (usually the root or ratio test helps us out with. For what values of x does the power (a.k.a. Taylor series is used to evaluate the value of a whole function in each point if the functional values and derivatives are identified at a single. They are not provided in. P1(x) = x f(n)(x0) (x x0)n n! Here is a set of practice problems to accompany the taylor series section of the series & sequences chapter of the notes for. Solved problems on taylor and maclaurin series finding taylor series to find taylor series of functions, we may: Questions regarding the taylor series expansion of univariate and multivariate functions, including coefficients and bounds on remainders. Using the estimate \( \dfrac{2^{10}}{10!}<0.000283\) we can use the taylor expansion of order 9 to estimate \( e^x\) at \( x=2\).
A Gentle Introduction to Taylor Series
Taylor Expansion Questions Converge (usually the root or ratio test helps us out with. Here is a set of practice problems to accompany the taylor series section of the series & sequences chapter of the notes for. Using the estimate \( \dfrac{2^{10}}{10!}<0.000283\) we can use the taylor expansion of order 9 to estimate \( e^x\) at \( x=2\). P1(x) = x f(n)(x0) (x x0)n n! For what values of x does the power (a.k.a. Solved problems on taylor and maclaurin series finding taylor series to find taylor series of functions, we may: Taylor series is used to evaluate the value of a whole function in each point if the functional values and derivatives are identified at a single. Converge (usually the root or ratio test helps us out with. A taylor series is an expansion of a function into an infinite sum of terms, where each term's exponent is larger and larger, like this: You have to remember the taylor series and the radius of convergence of ex, sin x, cos x, 1 1−x. They are not provided in. Questions regarding the taylor series expansion of univariate and multivariate functions, including coefficients and bounds on remainders.
From www.chegg.com
Solved Tutorial Exercise Find the Taylor series for f(x) Taylor Expansion Questions Solved problems on taylor and maclaurin series finding taylor series to find taylor series of functions, we may: P1(x) = x f(n)(x0) (x x0)n n! Converge (usually the root or ratio test helps us out with. For what values of x does the power (a.k.a. Using the estimate \( \dfrac{2^{10}}{10!}<0.000283\) we can use the taylor expansion of order 9 to. Taylor Expansion Questions.
From www.chegg.com
Solved Key Idea 32 Important Taylor Series Expansions Taylor Expansion Questions Solved problems on taylor and maclaurin series finding taylor series to find taylor series of functions, we may: Using the estimate \( \dfrac{2^{10}}{10!}<0.000283\) we can use the taylor expansion of order 9 to estimate \( e^x\) at \( x=2\). P1(x) = x f(n)(x0) (x x0)n n! Taylor series is used to evaluate the value of a whole function in each. Taylor Expansion Questions.
From www.chegg.com
Solved In this problem, we will use Taylor series expansions Taylor Expansion Questions A taylor series is an expansion of a function into an infinite sum of terms, where each term's exponent is larger and larger, like this: Using the estimate \( \dfrac{2^{10}}{10!}<0.000283\) we can use the taylor expansion of order 9 to estimate \( e^x\) at \( x=2\). Here is a set of practice problems to accompany the taylor series section of. Taylor Expansion Questions.
From www.chegg.com
Solved Which is the Taylor series expansion for cos (x) Taylor Expansion Questions Taylor series is used to evaluate the value of a whole function in each point if the functional values and derivatives are identified at a single. Using the estimate \( \dfrac{2^{10}}{10!}<0.000283\) we can use the taylor expansion of order 9 to estimate \( e^x\) at \( x=2\). Solved problems on taylor and maclaurin series finding taylor series to find taylor. Taylor Expansion Questions.
From www.chegg.com
Solved Find the Taylor series for f(x) centered at the given Taylor Expansion Questions Using the estimate \( \dfrac{2^{10}}{10!}<0.000283\) we can use the taylor expansion of order 9 to estimate \( e^x\) at \( x=2\). For what values of x does the power (a.k.a. Taylor series is used to evaluate the value of a whole function in each point if the functional values and derivatives are identified at a single. P1(x) = x f(n)(x0). Taylor Expansion Questions.
From www.chegg.com
Solved Problem 2 Taylor Series (25 points) a. Use first and Taylor Expansion Questions Questions regarding the taylor series expansion of univariate and multivariate functions, including coefficients and bounds on remainders. Converge (usually the root or ratio test helps us out with. Using the estimate \( \dfrac{2^{10}}{10!}<0.000283\) we can use the taylor expansion of order 9 to estimate \( e^x\) at \( x=2\). You have to remember the taylor series and the radius of. Taylor Expansion Questions.
From mathematica.stackexchange.com
How to obtain the Taylor expansion of any function? Mathematica Stack Taylor Expansion Questions Taylor series is used to evaluate the value of a whole function in each point if the functional values and derivatives are identified at a single. A taylor series is an expansion of a function into an infinite sum of terms, where each term's exponent is larger and larger, like this: Using the estimate \( \dfrac{2^{10}}{10!}<0.000283\) we can use the. Taylor Expansion Questions.
From fity.club
Taylor Series Expansion Of Natural Log Function Youtube Taylor Expansion Questions They are not provided in. For what values of x does the power (a.k.a. You have to remember the taylor series and the radius of convergence of ex, sin x, cos x, 1 1−x. A taylor series is an expansion of a function into an infinite sum of terms, where each term's exponent is larger and larger, like this: Here. Taylor Expansion Questions.
From www.slideserve.com
PPT NUMERICAL DIFFERENTIATION or DIFFERENCE APPROXIMATION PowerPoint Taylor Expansion Questions Converge (usually the root or ratio test helps us out with. Solved problems on taylor and maclaurin series finding taylor series to find taylor series of functions, we may: P1(x) = x f(n)(x0) (x x0)n n! For what values of x does the power (a.k.a. A taylor series is an expansion of a function into an infinite sum of terms,. Taylor Expansion Questions.
From fity.club
What Is The Taylor Series Expansion Of Mathexmath Taylor Expansion Questions Solved problems on taylor and maclaurin series finding taylor series to find taylor series of functions, we may: Converge (usually the root or ratio test helps us out with. Questions regarding the taylor series expansion of univariate and multivariate functions, including coefficients and bounds on remainders. A taylor series is an expansion of a function into an infinite sum of. Taylor Expansion Questions.
From www.chegg.com
Solved According to Taylor series expansion at x = 0, we Taylor Expansion Questions Converge (usually the root or ratio test helps us out with. P1(x) = x f(n)(x0) (x x0)n n! Here is a set of practice problems to accompany the taylor series section of the series & sequences chapter of the notes for. Taylor series is used to evaluate the value of a whole function in each point if the functional values. Taylor Expansion Questions.
From www.youtube.com
GATE 2020 TAYLOR EXPANSION QUESTION REAL ANALYSIS YouTube Taylor Expansion Questions Using the estimate \( \dfrac{2^{10}}{10!}<0.000283\) we can use the taylor expansion of order 9 to estimate \( e^x\) at \( x=2\). For what values of x does the power (a.k.a. They are not provided in. P1(x) = x f(n)(x0) (x x0)n n! Questions regarding the taylor series expansion of univariate and multivariate functions, including coefficients and bounds on remainders. Solved. Taylor Expansion Questions.
From math.stackexchange.com
how do I find the taylor polynomial of multivariable functions Taylor Expansion Questions Questions regarding the taylor series expansion of univariate and multivariate functions, including coefficients and bounds on remainders. Using the estimate \( \dfrac{2^{10}}{10!}<0.000283\) we can use the taylor expansion of order 9 to estimate \( e^x\) at \( x=2\). Taylor series is used to evaluate the value of a whole function in each point if the functional values and derivatives are. Taylor Expansion Questions.
From www.slideserve.com
PPT Ordinary Differential Equations PowerPoint Presentation, free Taylor Expansion Questions You have to remember the taylor series and the radius of convergence of ex, sin x, cos x, 1 1−x. Taylor series is used to evaluate the value of a whole function in each point if the functional values and derivatives are identified at a single. Questions regarding the taylor series expansion of univariate and multivariate functions, including coefficients and. Taylor Expansion Questions.
From math.stackexchange.com
Rearranging Taylor series to see Newton Raphson formula Mathematics Taylor Expansion Questions P1(x) = x f(n)(x0) (x x0)n n! They are not provided in. Taylor series is used to evaluate the value of a whole function in each point if the functional values and derivatives are identified at a single. Converge (usually the root or ratio test helps us out with. For what values of x does the power (a.k.a. Here is. Taylor Expansion Questions.
From www.chegg.com
Solved 11. The Taylor Series expansion for arctan(x) at x = Taylor Expansion Questions Taylor series is used to evaluate the value of a whole function in each point if the functional values and derivatives are identified at a single. They are not provided in. Using the estimate \( \dfrac{2^{10}}{10!}<0.000283\) we can use the taylor expansion of order 9 to estimate \( e^x\) at \( x=2\). You have to remember the taylor series and. Taylor Expansion Questions.
From www.chegg.com
Solved Q3 Use Taylor series expansion to prove the Taylor Expansion Questions Solved problems on taylor and maclaurin series finding taylor series to find taylor series of functions, we may: Using the estimate \( \dfrac{2^{10}}{10!}<0.000283\) we can use the taylor expansion of order 9 to estimate \( e^x\) at \( x=2\). P1(x) = x f(n)(x0) (x x0)n n! They are not provided in. Questions regarding the taylor series expansion of univariate and. Taylor Expansion Questions.
From math.stackexchange.com
multivariable calculus Using taylor expansion to show the negative of Taylor Expansion Questions Using the estimate \( \dfrac{2^{10}}{10!}<0.000283\) we can use the taylor expansion of order 9 to estimate \( e^x\) at \( x=2\). P1(x) = x f(n)(x0) (x x0)n n! Questions regarding the taylor series expansion of univariate and multivariate functions, including coefficients and bounds on remainders. A taylor series is an expansion of a function into an infinite sum of terms,. Taylor Expansion Questions.
From www.nagwa.com
Question Video Finding the Taylor Series Expansion of a Function from Taylor Expansion Questions Here is a set of practice problems to accompany the taylor series section of the series & sequences chapter of the notes for. Solved problems on taylor and maclaurin series finding taylor series to find taylor series of functions, we may: P1(x) = x f(n)(x0) (x x0)n n! Using the estimate \( \dfrac{2^{10}}{10!}<0.000283\) we can use the taylor expansion of. Taylor Expansion Questions.
From mathoverflow.net
reference request Taylor expansion with remainder on locally convex Taylor Expansion Questions Questions regarding the taylor series expansion of univariate and multivariate functions, including coefficients and bounds on remainders. Using the estimate \( \dfrac{2^{10}}{10!}<0.000283\) we can use the taylor expansion of order 9 to estimate \( e^x\) at \( x=2\). Converge (usually the root or ratio test helps us out with. P1(x) = x f(n)(x0) (x x0)n n! Taylor series is used. Taylor Expansion Questions.
From www.slideserve.com
PPT Financial Risk Management PowerPoint Presentation, free download Taylor Expansion Questions Taylor series is used to evaluate the value of a whole function in each point if the functional values and derivatives are identified at a single. A taylor series is an expansion of a function into an infinite sum of terms, where each term's exponent is larger and larger, like this: Solved problems on taylor and maclaurin series finding taylor. Taylor Expansion Questions.
From machinelearningmastery.com
A Gentle Introduction to Taylor Series Taylor Expansion Questions Here is a set of practice problems to accompany the taylor series section of the series & sequences chapter of the notes for. P1(x) = x f(n)(x0) (x x0)n n! A taylor series is an expansion of a function into an infinite sum of terms, where each term's exponent is larger and larger, like this: Solved problems on taylor and. Taylor Expansion Questions.
From www.chegg.com
Solved Problem 4) Evaluate exp(5) use the Taylor expansion Taylor Expansion Questions Questions regarding the taylor series expansion of univariate and multivariate functions, including coefficients and bounds on remainders. You have to remember the taylor series and the radius of convergence of ex, sin x, cos x, 1 1−x. Here is a set of practice problems to accompany the taylor series section of the series & sequences chapter of the notes for.. Taylor Expansion Questions.
From www.chegg.com
Taylor series expansion is normally used to Taylor Expansion Questions Converge (usually the root or ratio test helps us out with. For what values of x does the power (a.k.a. Solved problems on taylor and maclaurin series finding taylor series to find taylor series of functions, we may: Questions regarding the taylor series expansion of univariate and multivariate functions, including coefficients and bounds on remainders. Taylor series is used to. Taylor Expansion Questions.
From www.chegg.com
3 Taylor series for functions of two variables For a Taylor Expansion Questions Taylor series is used to evaluate the value of a whole function in each point if the functional values and derivatives are identified at a single. You have to remember the taylor series and the radius of convergence of ex, sin x, cos x, 1 1−x. P1(x) = x f(n)(x0) (x x0)n n! Questions regarding the taylor series expansion of. Taylor Expansion Questions.
From www.chegg.com
Solved Taylor series If a function f has a power series Taylor Expansion Questions P1(x) = x f(n)(x0) (x x0)n n! Solved problems on taylor and maclaurin series finding taylor series to find taylor series of functions, we may: Using the estimate \( \dfrac{2^{10}}{10!}<0.000283\) we can use the taylor expansion of order 9 to estimate \( e^x\) at \( x=2\). Here is a set of practice problems to accompany the taylor series section of. Taylor Expansion Questions.
From www.chegg.com
Solved Use this list of Basic Taylor Series and the identity Taylor Expansion Questions Taylor series is used to evaluate the value of a whole function in each point if the functional values and derivatives are identified at a single. They are not provided in. A taylor series is an expansion of a function into an infinite sum of terms, where each term's exponent is larger and larger, like this: Converge (usually the root. Taylor Expansion Questions.
From in.pinterest.com
Pin on math Taylor Expansion Questions Taylor series is used to evaluate the value of a whole function in each point if the functional values and derivatives are identified at a single. You have to remember the taylor series and the radius of convergence of ex, sin x, cos x, 1 1−x. For what values of x does the power (a.k.a. A taylor series is an. Taylor Expansion Questions.
From www.chegg.com
These are (obviously) functions represented as power Taylor Expansion Questions Solved problems on taylor and maclaurin series finding taylor series to find taylor series of functions, we may: Converge (usually the root or ratio test helps us out with. They are not provided in. Here is a set of practice problems to accompany the taylor series section of the series & sequences chapter of the notes for. Questions regarding the. Taylor Expansion Questions.
From www.youtube.com
Expansion of cot x important Questions solved YouTube Taylor Expansion Questions Here is a set of practice problems to accompany the taylor series section of the series & sequences chapter of the notes for. Solved problems on taylor and maclaurin series finding taylor series to find taylor series of functions, we may: Using the estimate \( \dfrac{2^{10}}{10!}<0.000283\) we can use the taylor expansion of order 9 to estimate \( e^x\) at. Taylor Expansion Questions.
From www.youtube.com
What motivates Taylor expansion? YouTube Taylor Expansion Questions Taylor series is used to evaluate the value of a whole function in each point if the functional values and derivatives are identified at a single. You have to remember the taylor series and the radius of convergence of ex, sin x, cos x, 1 1−x. For what values of x does the power (a.k.a. Converge (usually the root or. Taylor Expansion Questions.
From math.stackexchange.com
calculus Statistical PhysicsTaylor expanding Mathematics Stack Taylor Expansion Questions Taylor series is used to evaluate the value of a whole function in each point if the functional values and derivatives are identified at a single. Questions regarding the taylor series expansion of univariate and multivariate functions, including coefficients and bounds on remainders. P1(x) = x f(n)(x0) (x x0)n n! Converge (usually the root or ratio test helps us out. Taylor Expansion Questions.
From snotext.weebly.com
Using taylor series to find the sum of a series. snotext Taylor Expansion Questions Here is a set of practice problems to accompany the taylor series section of the series & sequences chapter of the notes for. You have to remember the taylor series and the radius of convergence of ex, sin x, cos x, 1 1−x. Converge (usually the root or ratio test helps us out with. They are not provided in. Solved. Taylor Expansion Questions.
From www.chegg.com
3 Taylor series for functions of two variables For a Taylor Expansion Questions A taylor series is an expansion of a function into an infinite sum of terms, where each term's exponent is larger and larger, like this: Here is a set of practice problems to accompany the taylor series section of the series & sequences chapter of the notes for. Solved problems on taylor and maclaurin series finding taylor series to find. Taylor Expansion Questions.
From math.stackexchange.com
calculus question about taylor series Mathematics Stack Exchange Taylor Expansion Questions They are not provided in. Solved problems on taylor and maclaurin series finding taylor series to find taylor series of functions, we may: Taylor series is used to evaluate the value of a whole function in each point if the functional values and derivatives are identified at a single. Here is a set of practice problems to accompany the taylor. Taylor Expansion Questions.