Points Of Inflection F(X) Are . For a function \ (f (x),\) its concavity can be measured by its second order. The concavity is related to the second. an inflection point is where a curve changes from concave up to concave down, or vice versa. differentiate the function, f (x), to obtain f '(x). when the second derivative is negative, the function is concave downward. Solve the equation f '(x) = 0 for x to get the values of x at minima or maxima or. And the inflection point is where it goes from concave upward to concave downward (or. It means that the function changes from. a curve's inflection point is the point at which the curve's concavity changes. an inflection point occurs when the sign of the second derivative of a function, f (x), changes from positive to negative (or vice versa) at a point where f (x) = 0 or. the point of inflection or inflection point is a point in which the concavity of the function changes.
from www.chegg.com
the point of inflection or inflection point is a point in which the concavity of the function changes. Solve the equation f '(x) = 0 for x to get the values of x at minima or maxima or. a curve's inflection point is the point at which the curve's concavity changes. And the inflection point is where it goes from concave upward to concave downward (or. It means that the function changes from. For a function \ (f (x),\) its concavity can be measured by its second order. an inflection point occurs when the sign of the second derivative of a function, f (x), changes from positive to negative (or vice versa) at a point where f (x) = 0 or. when the second derivative is negative, the function is concave downward. The concavity is related to the second. an inflection point is where a curve changes from concave up to concave down, or vice versa.
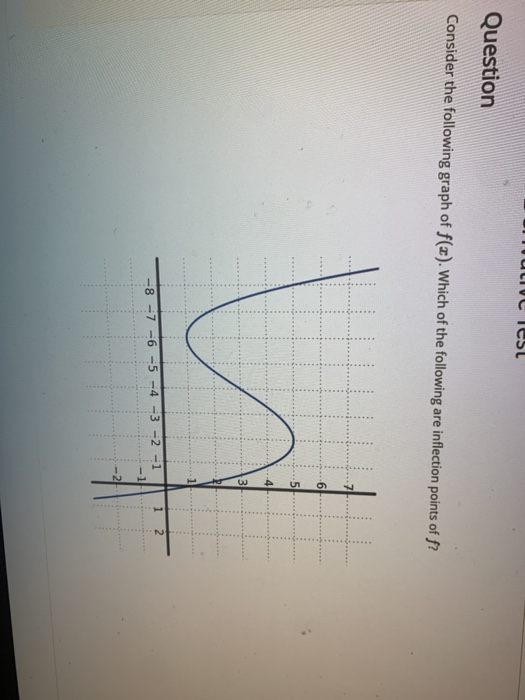
Solved ICSL Question Consider the following graph of f(x).
Points Of Inflection F(X) Are differentiate the function, f (x), to obtain f '(x). an inflection point is where a curve changes from concave up to concave down, or vice versa. the point of inflection or inflection point is a point in which the concavity of the function changes. Solve the equation f '(x) = 0 for x to get the values of x at minima or maxima or. For a function \ (f (x),\) its concavity can be measured by its second order. differentiate the function, f (x), to obtain f '(x). And the inflection point is where it goes from concave upward to concave downward (or. The concavity is related to the second. an inflection point occurs when the sign of the second derivative of a function, f (x), changes from positive to negative (or vice versa) at a point where f (x) = 0 or. a curve's inflection point is the point at which the curve's concavity changes. when the second derivative is negative, the function is concave downward. It means that the function changes from.
From www.chegg.com
Solved Consider the graph of f(x) below. Determine the signs Points Of Inflection F(X) Are Solve the equation f '(x) = 0 for x to get the values of x at minima or maxima or. the point of inflection or inflection point is a point in which the concavity of the function changes. an inflection point is where a curve changes from concave up to concave down, or vice versa. differentiate the. Points Of Inflection F(X) Are.
From www.chegg.com
Solved Based on the above graph of the second derivative of Points Of Inflection F(X) Are the point of inflection or inflection point is a point in which the concavity of the function changes. an inflection point is where a curve changes from concave up to concave down, or vice versa. And the inflection point is where it goes from concave upward to concave downward (or. For a function \ (f (x),\) its concavity. Points Of Inflection F(X) Are.
From math.stackexchange.com
real analysis Reconstructing a function from its critical points and Points Of Inflection F(X) Are And the inflection point is where it goes from concave upward to concave downward (or. It means that the function changes from. For a function \ (f (x),\) its concavity can be measured by its second order. when the second derivative is negative, the function is concave downward. the point of inflection or inflection point is a point. Points Of Inflection F(X) Are.
From www.reddit.com
Why are these the points of inflection incorrect? r/calculus Points Of Inflection F(X) Are when the second derivative is negative, the function is concave downward. the point of inflection or inflection point is a point in which the concavity of the function changes. differentiate the function, f (x), to obtain f '(x). an inflection point is where a curve changes from concave up to concave down, or vice versa. And. Points Of Inflection F(X) Are.
From www.chegg.com
Solved (1 point) Use a graph below of f(x) = 3e9x2 to Points Of Inflection F(X) Are when the second derivative is negative, the function is concave downward. And the inflection point is where it goes from concave upward to concave downward (or. an inflection point is where a curve changes from concave up to concave down, or vice versa. a curve's inflection point is the point at which the curve's concavity changes. Solve. Points Of Inflection F(X) Are.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Points Of Inflection F(X) Are It means that the function changes from. differentiate the function, f (x), to obtain f '(x). when the second derivative is negative, the function is concave downward. Solve the equation f '(x) = 0 for x to get the values of x at minima or maxima or. And the inflection point is where it goes from concave upward. Points Of Inflection F(X) Are.
From www.chegg.com
Solved Consider the following graph of f(x). Use the slider Points Of Inflection F(X) Are an inflection point occurs when the sign of the second derivative of a function, f (x), changes from positive to negative (or vice versa) at a point where f (x) = 0 or. differentiate the function, f (x), to obtain f '(x). For a function \ (f (x),\) its concavity can be measured by its second order. . Points Of Inflection F(X) Are.
From www.chegg.com
Solved (f) Give the inflection points of f(x). Enter your Points Of Inflection F(X) Are And the inflection point is where it goes from concave upward to concave downward (or. It means that the function changes from. Solve the equation f '(x) = 0 for x to get the values of x at minima or maxima or. differentiate the function, f (x), to obtain f '(x). The concavity is related to the second. . Points Of Inflection F(X) Are.
From www.chegg.com
Solved In each part state the xcoordinates of the Points Of Inflection F(X) Are Solve the equation f '(x) = 0 for x to get the values of x at minima or maxima or. The concavity is related to the second. For a function \ (f (x),\) its concavity can be measured by its second order. differentiate the function, f (x), to obtain f '(x). a curve's inflection point is the point. Points Of Inflection F(X) Are.
From www.youtube.com
Points of Inflection from f(x)=cos(2x) YouTube Points Of Inflection F(X) Are the point of inflection or inflection point is a point in which the concavity of the function changes. an inflection point occurs when the sign of the second derivative of a function, f (x), changes from positive to negative (or vice versa) at a point where f (x) = 0 or. Solve the equation f '(x) = 0. Points Of Inflection F(X) Are.
From www.chegg.com
Solved ICSL Question Consider the following graph of f(x). Points Of Inflection F(X) Are a curve's inflection point is the point at which the curve's concavity changes. The concavity is related to the second. an inflection point is where a curve changes from concave up to concave down, or vice versa. Solve the equation f '(x) = 0 for x to get the values of x at minima or maxima or. For. Points Of Inflection F(X) Are.
From www.numerade.com
SOLVEDpoint) Determine the intervals on which the function f(x) = 3x2 Points Of Inflection F(X) Are an inflection point is where a curve changes from concave up to concave down, or vice versa. For a function \ (f (x),\) its concavity can be measured by its second order. differentiate the function, f (x), to obtain f '(x). when the second derivative is negative, the function is concave downward. And the inflection point is. Points Of Inflection F(X) Are.
From www.youtube.com
Finding max/min/inflection pts given the graph of f '(x) or f ''(x Points Of Inflection F(X) Are For a function \ (f (x),\) its concavity can be measured by its second order. The concavity is related to the second. It means that the function changes from. the point of inflection or inflection point is a point in which the concavity of the function changes. Solve the equation f '(x) = 0 for x to get the. Points Of Inflection F(X) Are.
From www.chegg.com
Solved QUESTION 2 . 1 POINT Consider the following graph of Points Of Inflection F(X) Are For a function \ (f (x),\) its concavity can be measured by its second order. The concavity is related to the second. And the inflection point is where it goes from concave upward to concave downward (or. an inflection point is where a curve changes from concave up to concave down, or vice versa. when the second derivative. Points Of Inflection F(X) Are.
From in.eteachers.edu.vn
Details 122+ khan academy curve sketching super hot in.eteachers Points Of Inflection F(X) Are a curve's inflection point is the point at which the curve's concavity changes. an inflection point occurs when the sign of the second derivative of a function, f (x), changes from positive to negative (or vice versa) at a point where f (x) = 0 or. It means that the function changes from. when the second derivative. Points Of Inflection F(X) Are.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Points Of Inflection F(X) Are For a function \ (f (x),\) its concavity can be measured by its second order. when the second derivative is negative, the function is concave downward. And the inflection point is where it goes from concave upward to concave downward (or. Solve the equation f '(x) = 0 for x to get the values of x at minima or. Points Of Inflection F(X) Are.
From www.wikihow.com
5 Ways to Find Inflection Points wikiHow Points Of Inflection F(X) Are differentiate the function, f (x), to obtain f '(x). when the second derivative is negative, the function is concave downward. the point of inflection or inflection point is a point in which the concavity of the function changes. an inflection point occurs when the sign of the second derivative of a function, f (x), changes from. Points Of Inflection F(X) Are.
From www.chegg.com
Solved Determine the number of points of inflection for the Points Of Inflection F(X) Are And the inflection point is where it goes from concave upward to concave downward (or. an inflection point occurs when the sign of the second derivative of a function, f (x), changes from positive to negative (or vice versa) at a point where f (x) = 0 or. Solve the equation f '(x) = 0 for x to get. Points Of Inflection F(X) Are.
From socratic.org
How do you find all points of inflection for f(x)=x^46x^3? Socratic Points Of Inflection F(X) Are For a function \ (f (x),\) its concavity can be measured by its second order. And the inflection point is where it goes from concave upward to concave downward (or. differentiate the function, f (x), to obtain f '(x). an inflection point occurs when the sign of the second derivative of a function, f (x), changes from positive. Points Of Inflection F(X) Are.
From giookivgt.blob.core.windows.net
Points Of Inflection From F Prime Graph at William Wolford blog Points Of Inflection F(X) Are And the inflection point is where it goes from concave upward to concave downward (or. the point of inflection or inflection point is a point in which the concavity of the function changes. a curve's inflection point is the point at which the curve's concavity changes. differentiate the function, f (x), to obtain f '(x). It means. Points Of Inflection F(X) Are.
From exyzrtren.blob.core.windows.net
Points Of Inflection Structure at Glenna Appling blog Points Of Inflection F(X) Are It means that the function changes from. an inflection point occurs when the sign of the second derivative of a function, f (x), changes from positive to negative (or vice versa) at a point where f (x) = 0 or. differentiate the function, f (x), to obtain f '(x). Solve the equation f '(x) = 0 for x. Points Of Inflection F(X) Are.
From www.youtube.com
Given a graph of f' learn to find the points of inflection YouTube Points Of Inflection F(X) Are For a function \ (f (x),\) its concavity can be measured by its second order. Solve the equation f '(x) = 0 for x to get the values of x at minima or maxima or. a curve's inflection point is the point at which the curve's concavity changes. It means that the function changes from. And the inflection point. Points Of Inflection F(X) Are.
From www.savemyexams.com
Points of Inflection AQA A Level Maths Pure Revision Notes 2018 Points Of Inflection F(X) Are when the second derivative is negative, the function is concave downward. It means that the function changes from. a curve's inflection point is the point at which the curve's concavity changes. The concavity is related to the second. Solve the equation f '(x) = 0 for x to get the values of x at minima or maxima or.. Points Of Inflection F(X) Are.
From www.chegg.com
Solved State the xcoordinates of the inflection points of Points Of Inflection F(X) Are an inflection point is where a curve changes from concave up to concave down, or vice versa. Solve the equation f '(x) = 0 for x to get the values of x at minima or maxima or. the point of inflection or inflection point is a point in which the concavity of the function changes. For a function. Points Of Inflection F(X) Are.
From www.chegg.com
Solved Determine the points of inflection f(x) Interval Test Points Of Inflection F(X) Are a curve's inflection point is the point at which the curve's concavity changes. It means that the function changes from. an inflection point occurs when the sign of the second derivative of a function, f (x), changes from positive to negative (or vice versa) at a point where f (x) = 0 or. differentiate the function, f. Points Of Inflection F(X) Are.
From exynjdmqg.blob.core.windows.net
Point Of Inflection Find X at Ross Weems blog Points Of Inflection F(X) Are And the inflection point is where it goes from concave upward to concave downward (or. Solve the equation f '(x) = 0 for x to get the values of x at minima or maxima or. the point of inflection or inflection point is a point in which the concavity of the function changes. when the second derivative is. Points Of Inflection F(X) Are.
From www.chegg.com
Solved In each part state the xcoordinates of the Points Of Inflection F(X) Are an inflection point occurs when the sign of the second derivative of a function, f (x), changes from positive to negative (or vice versa) at a point where f (x) = 0 or. an inflection point is where a curve changes from concave up to concave down, or vice versa. a curve's inflection point is the point. Points Of Inflection F(X) Are.
From socratic.org
How do you find all points of inflection for f(x) = (1/12)x^4 2x^2 Points Of Inflection F(X) Are an inflection point is where a curve changes from concave up to concave down, or vice versa. an inflection point occurs when the sign of the second derivative of a function, f (x), changes from positive to negative (or vice versa) at a point where f (x) = 0 or. The concavity is related to the second. . Points Of Inflection F(X) Are.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Points Of Inflection F(X) Are It means that the function changes from. the point of inflection or inflection point is a point in which the concavity of the function changes. Solve the equation f '(x) = 0 for x to get the values of x at minima or maxima or. And the inflection point is where it goes from concave upward to concave downward. Points Of Inflection F(X) Are.
From www.youtube.com
Find intervals of concavity and inflection points for f = x/x^2+1 Local Points Of Inflection F(X) Are The concavity is related to the second. a curve's inflection point is the point at which the curve's concavity changes. when the second derivative is negative, the function is concave downward. an inflection point occurs when the sign of the second derivative of a function, f (x), changes from positive to negative (or vice versa) at a. Points Of Inflection F(X) Are.
From socratic.org
If f " (x) = x(x+1)(x2)^2, what are the xcoordinates of the points of Points Of Inflection F(X) Are an inflection point occurs when the sign of the second derivative of a function, f (x), changes from positive to negative (or vice versa) at a point where f (x) = 0 or. when the second derivative is negative, the function is concave downward. differentiate the function, f (x), to obtain f '(x). It means that the. Points Of Inflection F(X) Are.
From www.youtube.com
Calculus I Inflection points from the graph of f'' YouTube Points Of Inflection F(X) Are Solve the equation f '(x) = 0 for x to get the values of x at minima or maxima or. It means that the function changes from. when the second derivative is negative, the function is concave downward. The concavity is related to the second. For a function \ (f (x),\) its concavity can be measured by its second. Points Of Inflection F(X) Are.
From www.mashupmath.com
How to Graph a Function in 3 Easy Steps — Mashup Math Points Of Inflection F(X) Are The concavity is related to the second. Solve the equation f '(x) = 0 for x to get the values of x at minima or maxima or. an inflection point is where a curve changes from concave up to concave down, or vice versa. a curve's inflection point is the point at which the curve's concavity changes. . Points Of Inflection F(X) Are.
From www.chegg.com
Solved State the xcoordinates of the inflection points of Points Of Inflection F(X) Are a curve's inflection point is the point at which the curve's concavity changes. The concavity is related to the second. an inflection point is where a curve changes from concave up to concave down, or vice versa. differentiate the function, f (x), to obtain f '(x). the point of inflection or inflection point is a point. Points Of Inflection F(X) Are.
From socratic.org
What are the inflection points for (x^2)/(x^2+1)? Socratic Points Of Inflection F(X) Are an inflection point is where a curve changes from concave up to concave down, or vice versa. when the second derivative is negative, the function is concave downward. an inflection point occurs when the sign of the second derivative of a function, f (x), changes from positive to negative (or vice versa) at a point where f. Points Of Inflection F(X) Are.