Definition Of Derivative Cos X . We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. The proof begins by stating the definition of the derivative of a real function at a point. In this case, it’s the derivative of cos (x) with respect to x,. We'll need the following facts: D dx sin (x) = cos (x) d dx cos (x) = −sin (x) d dx tan (x) = sec 2 (x) did they just drop out of the sky? In this video, we dive into the proof of the derivative of cos (x) using limit definition of the. The three most useful derivatives in trigonometry are: Can we prove them somehow? We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier.
from www.profmatt.com
The proof begins by stating the definition of the derivative of a real function at a point. In this video, we dive into the proof of the derivative of cos (x) using limit definition of the. We'll need the following facts: We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. In this case, it’s the derivative of cos (x) with respect to x,. The three most useful derivatives in trigonometry are: D dx sin (x) = cos (x) d dx cos (x) = −sin (x) d dx tan (x) = sec 2 (x) did they just drop out of the sky? Can we prove them somehow? We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier.
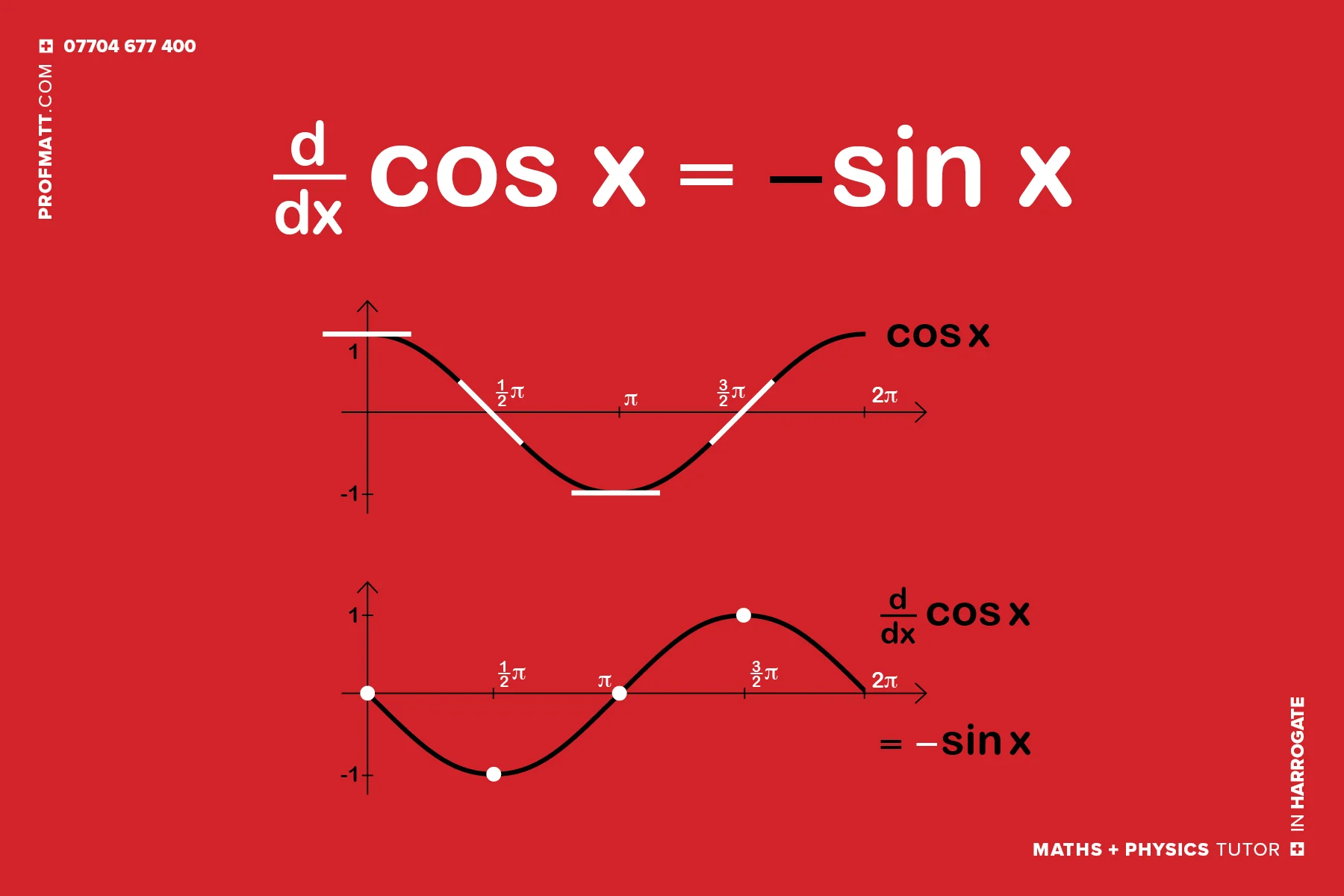
cribsheets — Matthew Handy Maths + Physics tutor in Harrogate
Definition Of Derivative Cos X We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. In this video, we dive into the proof of the derivative of cos (x) using limit definition of the. In this case, it’s the derivative of cos (x) with respect to x,. The three most useful derivatives in trigonometry are: We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. D dx sin (x) = cos (x) d dx cos (x) = −sin (x) d dx tan (x) = sec 2 (x) did they just drop out of the sky? The proof begins by stating the definition of the derivative of a real function at a point. We'll need the following facts: Can we prove them somehow? We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier.
From study.com
What is the Derivative of 1/cos(x)? Lesson Definition Of Derivative Cos X The proof begins by stating the definition of the derivative of a real function at a point. In this case, it’s the derivative of cos (x) with respect to x,. We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. Can we prove them somehow? We'll need. Definition Of Derivative Cos X.
From www.teachoo.com
Misc 16 Find derivative cos x / 1 + sin x Class 11 Derivatives Definition Of Derivative Cos X We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. The three most useful derivatives in trigonometry are: We'll need the following facts: Can. Definition Of Derivative Cos X.
From www.youtube.com
Derivative of Cos(x) Proof (Using the Limit Definition) YouTube Definition Of Derivative Cos X We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. The proof begins by stating the definition of the derivative of a real function at a point. The three most useful derivatives in trigonometry are: Can we prove them somehow? D dx sin (x) = cos (x). Definition Of Derivative Cos X.
From www.youtube.com
Derivative of Cos(x) using First Principle DEFINITION OF DERIVATIVE Definition Of Derivative Cos X We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. In this video, we dive into the proof of the derivative of cos (x) using limit definition of the. In this case, it’s the derivative of cos (x) with respect to x,. The three most useful derivatives. Definition Of Derivative Cos X.
From www.youtube.com
The PROOF that the Derivative of sin(x) is cos(x)!!! Limit Definition Definition Of Derivative Cos X In this case, it’s the derivative of cos (x) with respect to x,. The three most useful derivatives in trigonometry are: In this video, we dive into the proof of the derivative of cos (x) using limit definition of the. We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit. Definition Of Derivative Cos X.
From www.youtube.com
Proof that the Derivative of cos(x) is sin(x) using the Limit Definition Of Derivative Cos X We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. The three most useful derivatives in trigonometry are: The proof begins by stating the definition of the derivative of a real function at a point. We can find the derivatives of \(\sin x\) and \(\cos x\) by. Definition Of Derivative Cos X.
From www.yawin.in
Find the derivatives of cos x from the first principle Yawin Definition Of Derivative Cos X We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. Can we prove them somehow? The three most useful derivatives in trigonometry are: The proof begins by stating the definition of the derivative of a real function at a point. We can find the derivatives of \(\sin. Definition Of Derivative Cos X.
From evgenii.com
Basic derivatives Definition Of Derivative Cos X In this video, we dive into the proof of the derivative of cos (x) using limit definition of the. D dx sin (x) = cos (x) d dx cos (x) = −sin (x) d dx tan (x) = sec 2 (x) did they just drop out of the sky? Can we prove them somehow? We can find the derivatives of. Definition Of Derivative Cos X.
From www.youtube.com
How to Find the Derivative of a^x from First Principles YouTube Definition Of Derivative Cos X In this video, we dive into the proof of the derivative of cos (x) using limit definition of the. Can we prove them somehow? The three most useful derivatives in trigonometry are: We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. We can find the derivatives. Definition Of Derivative Cos X.
From www.youtube.com
what’s the derivative of (cos(x))^x? YouTube Definition Of Derivative Cos X D dx sin (x) = cos (x) d dx cos (x) = −sin (x) d dx tan (x) = sec 2 (x) did they just drop out of the sky? We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. We can find the derivatives of \(\sin. Definition Of Derivative Cos X.
From kunduz.com
Derivative of Cos(x) Formula, Proof in Easy Steps, Formula, Solved Definition Of Derivative Cos X In this video, we dive into the proof of the derivative of cos (x) using limit definition of the. We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and. Definition Of Derivative Cos X.
From www.teachoo.com
Example 22 Find the derivative of (x^5 cos x) / sin x Teachoo Definition Of Derivative Cos X We'll need the following facts: In this case, it’s the derivative of cos (x) with respect to x,. D dx sin (x) = cos (x) d dx cos (x) = −sin (x) d dx tan (x) = sec 2 (x) did they just drop out of the sky? We can find the derivatives of \(\sin x\) and \(\cos x\) by. Definition Of Derivative Cos X.
From www.youtube.com
How to Find the Derivative of cos2x from First Principles YouTube Definition Of Derivative Cos X We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. D dx sin (x) = cos (x) d dx cos (x) = −sin (x). Definition Of Derivative Cos X.
From www.slideserve.com
PPT Derivatives of Sine and Cosine PowerPoint Presentation, free Definition Of Derivative Cos X The three most useful derivatives in trigonometry are: In this video, we dive into the proof of the derivative of cos (x) using limit definition of the. The proof begins by stating the definition of the derivative of a real function at a point. We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of. Definition Of Derivative Cos X.
From www.teachoo.com
Differentiation of cos inverse x (cos^1 x) Teachoo [with Video] Definition Of Derivative Cos X In this case, it’s the derivative of cos (x) with respect to x,. The proof begins by stating the definition of the derivative of a real function at a point. In this video, we dive into the proof of the derivative of cos (x) using limit definition of the. We'll need the following facts: D dx sin (x) = cos. Definition Of Derivative Cos X.
From www.youtube.com
Proof of the derivatives of sin(x) and cos(x) using the limit Definition Of Derivative Cos X The three most useful derivatives in trigonometry are: D dx sin (x) = cos (x) d dx cos (x) = −sin (x) d dx tan (x) = sec 2 (x) did they just drop out of the sky? In this case, it’s the derivative of cos (x) with respect to x,. In this video, we dive into the proof of. Definition Of Derivative Cos X.
From derivativeit.com
The Derivative of cos^3x DerivativeIt Definition Of Derivative Cos X We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. The proof begins by stating the definition of the derivative of a real function at a point. We'll need the following facts: We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition. Definition Of Derivative Cos X.
From www.youtube.com
Derivative of cos(3x) from First Principles YouTube Definition Of Derivative Cos X The three most useful derivatives in trigonometry are: In this video, we dive into the proof of the derivative of cos (x) using limit definition of the. We'll need the following facts: In this case, it’s the derivative of cos (x) with respect to x,. We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition. Definition Of Derivative Cos X.
From www.teachoo.com
Ex 12.2, 10 Find derivative of cos x from first principle Teachoo Definition Of Derivative Cos X We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. We'll need the following facts: In this case, it’s the derivative of cos (x) with respect to x,. The three most useful derivatives in trigonometry are: We can find the derivatives of \(\sin x\) and \(\cos x\). Definition Of Derivative Cos X.
From www.youtube.com
Proof of the derivative of cosx A StepbyStep Proof and Explanation Definition Of Derivative Cos X The three most useful derivatives in trigonometry are: We'll need the following facts: Can we prove them somehow? In this case, it’s the derivative of cos (x) with respect to x,. We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. The proof begins by stating the. Definition Of Derivative Cos X.
From epsilonify.com
Derivative of cos(x) using First Principle of Derivatives [FULL PROOF] Definition Of Derivative Cos X In this case, it’s the derivative of cos (x) with respect to x,. Can we prove them somehow? We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. The proof begins by stating the definition of the derivative of a real function at a point. We can. Definition Of Derivative Cos X.
From kunduz.com
Differentiation of Trigonometric Functions Kunduz Definition Of Derivative Cos X We'll need the following facts: The three most useful derivatives in trigonometry are: Can we prove them somehow? D dx sin (x) = cos (x) d dx cos (x) = −sin (x) d dx tan (x) = sec 2 (x) did they just drop out of the sky? In this case, it’s the derivative of cos (x) with respect to. Definition Of Derivative Cos X.
From studylib.net
Derivative of cos x. Definition Of Derivative Cos X The proof begins by stating the definition of the derivative of a real function at a point. We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. Can we prove them somehow? In this case, it’s the derivative of cos (x) with respect to x,. We'll need. Definition Of Derivative Cos X.
From www.cuemath.com
Derivatives Calculus, Meaning, Interpretation Definition Of Derivative Cos X We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. We'll need the following facts: D dx sin (x) = cos (x) d dx cos (x) = −sin (x) d dx tan (x) = sec 2 (x) did they just drop out of the sky? We can. Definition Of Derivative Cos X.
From study.com
Differentiating f(x)=cosx Using a Specific Rule Calculus Definition Of Derivative Cos X We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. In this case, it’s the derivative of cos (x) with respect to x,. D dx sin (x) = cos (x) d dx cos (x) = −sin (x) d dx tan (x) = sec 2 (x) did they. Definition Of Derivative Cos X.
From www.teachoo.com
Ex 12.2, 10 Find derivative of cos x from first principle Teachoo Definition Of Derivative Cos X The three most useful derivatives in trigonometry are: In this case, it’s the derivative of cos (x) with respect to x,. The proof begins by stating the definition of the derivative of a real function at a point. We'll need the following facts: Can we prove them somehow? D dx sin (x) = cos (x) d dx cos (x) =. Definition Of Derivative Cos X.
From www.teachoo.com
Find the Derivative of cos1 x (Cos inverse x) Teachoo Definition Of Derivative Cos X We'll need the following facts: The proof begins by stating the definition of the derivative of a real function at a point. In this video, we dive into the proof of the derivative of cos (x) using limit definition of the. The three most useful derivatives in trigonometry are: We can find the derivatives of \(\sin x\) and \(\cos x\). Definition Of Derivative Cos X.
From en.neurochispas.com
Derivative of Cosine, cos(x) Formula, Proof, and Graphs Neurochispas Definition Of Derivative Cos X In this case, it’s the derivative of cos (x) with respect to x,. We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. We'll need the following facts: We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the. Definition Of Derivative Cos X.
From www.teachoo.com
Ex 12.2, 10 Find derivative of cos x from first principle Teachoo Definition Of Derivative Cos X The proof begins by stating the definition of the derivative of a real function at a point. The three most useful derivatives in trigonometry are: In this case, it’s the derivative of cos (x) with respect to x,. We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found. Definition Of Derivative Cos X.
From www.youtube.com
Derivative of cos(x) to 46th derivative. YouTube Definition Of Derivative Cos X In this video, we dive into the proof of the derivative of cos (x) using limit definition of the. We'll need the following facts: We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. D dx sin (x) = cos (x) d dx cos (x) = −sin. Definition Of Derivative Cos X.
From www.youtube.com
Calculus Made Easy Derivative of ln(cos(x)) Using the Chain Rule YouTube Definition Of Derivative Cos X In this video, we dive into the proof of the derivative of cos (x) using limit definition of the. Can we prove them somehow? D dx sin (x) = cos (x) d dx cos (x) = −sin (x) d dx tan (x) = sec 2 (x) did they just drop out of the sky? We'll need the following facts: We. Definition Of Derivative Cos X.
From derivativeit.com
The Derivative of Cos DerivativeIt Definition Of Derivative Cos X Can we prove them somehow? In this video, we dive into the proof of the derivative of cos (x) using limit definition of the. The three most useful derivatives in trigonometry are: D dx sin (x) = cos (x) d dx cos (x) = −sin (x) d dx tan (x) = sec 2 (x) did they just drop out of. Definition Of Derivative Cos X.
From delaneytiveburch.blogspot.com
Derivative of Cos X Definition Of Derivative Cos X D dx sin (x) = cos (x) d dx cos (x) = −sin (x) d dx tan (x) = sec 2 (x) did they just drop out of the sky? In this video, we dive into the proof of the derivative of cos (x) using limit definition of the. In this case, it’s the derivative of cos (x) with respect. Definition Of Derivative Cos X.
From www.profmatt.com
cribsheets — Matthew Handy Maths + Physics tutor in Harrogate Definition Of Derivative Cos X We'll need the following facts: Can we prove them somehow? We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. D dx sin (x) = cos (x) d dx cos (x) = −sin (x) d dx tan (x) = sec 2 (x) did they just drop out. Definition Of Derivative Cos X.
From www.youtube.com
derivation of the derivative of cos x using limits proof d/dx cos x Definition Of Derivative Cos X The proof begins by stating the definition of the derivative of a real function at a point. In this case, it’s the derivative of cos (x) with respect to x,. We can find the derivatives of \(\sin x\) and \(\cos x\) by using the definition of derivative and the limit formulas found earlier. The three most useful derivatives in trigonometry. Definition Of Derivative Cos X.
.jpg)