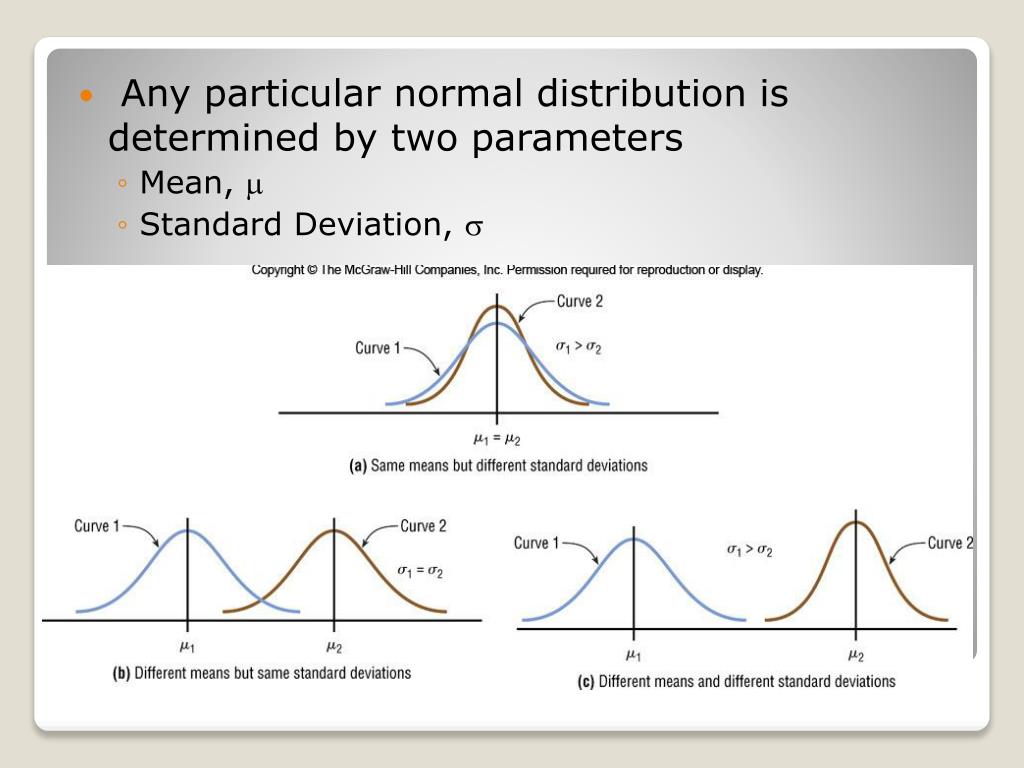
Two Parameter Normal Model . This lecture shows how to apply the basic principles of bayesian inference to the problem of estimating the parameters (mean and variance) of a normal distribution. When the model is indexed by multiple parameters, we need some extension of our de nitions of the fisher information and the je reys prior. The gaussian distribution does not have just one form. The normal distribution has two parameters, the mean and standard deviation. Instead, the shape changes based on. The normal distribution model always describes a symmetric, unimodal, bell shaped curve. Each of the pivot variables \( z \), \( t \), and \( v \) can be used to construct confidence sets for \( (\mu, \sigma) \). However, these curves can look. Normal distributions are defined by two parameters, the mean (\(\mu\)) and the standard deviation (\(\sigma\)).
from www.slideserve.com
Each of the pivot variables \( z \), \( t \), and \( v \) can be used to construct confidence sets for \( (\mu, \sigma) \). The normal distribution model always describes a symmetric, unimodal, bell shaped curve. The gaussian distribution does not have just one form. However, these curves can look. Normal distributions are defined by two parameters, the mean (\(\mu\)) and the standard deviation (\(\sigma\)). This lecture shows how to apply the basic principles of bayesian inference to the problem of estimating the parameters (mean and variance) of a normal distribution. The normal distribution has two parameters, the mean and standard deviation. Instead, the shape changes based on. When the model is indexed by multiple parameters, we need some extension of our de nitions of the fisher information and the je reys prior.
PPT The Normal Distribution PowerPoint Presentation, free download
Two Parameter Normal Model Instead, the shape changes based on. Each of the pivot variables \( z \), \( t \), and \( v \) can be used to construct confidence sets for \( (\mu, \sigma) \). The gaussian distribution does not have just one form. This lecture shows how to apply the basic principles of bayesian inference to the problem of estimating the parameters (mean and variance) of a normal distribution. Normal distributions are defined by two parameters, the mean (\(\mu\)) and the standard deviation (\(\sigma\)). The normal distribution has two parameters, the mean and standard deviation. The normal distribution model always describes a symmetric, unimodal, bell shaped curve. Instead, the shape changes based on. However, these curves can look. When the model is indexed by multiple parameters, we need some extension of our de nitions of the fisher information and the je reys prior.
From www.ashokcharan.com
Normal Distribution Two Parameter Normal Model Normal distributions are defined by two parameters, the mean (\(\mu\)) and the standard deviation (\(\sigma\)). However, these curves can look. The normal distribution has two parameters, the mean and standard deviation. This lecture shows how to apply the basic principles of bayesian inference to the problem of estimating the parameters (mean and variance) of a normal distribution. The normal distribution. Two Parameter Normal Model.
From www.researchgate.net
A Basic sigmoid function with two parameters (c1 and c2) as commonly Two Parameter Normal Model The gaussian distribution does not have just one form. When the model is indexed by multiple parameters, we need some extension of our de nitions of the fisher information and the je reys prior. Normal distributions are defined by two parameters, the mean (\(\mu\)) and the standard deviation (\(\sigma\)). However, these curves can look. Each of the pivot variables \(. Two Parameter Normal Model.
From www.researchgate.net
Frequency curve of twoparameter logistic type distribution Download Two Parameter Normal Model The gaussian distribution does not have just one form. The normal distribution model always describes a symmetric, unimodal, bell shaped curve. Instead, the shape changes based on. However, these curves can look. When the model is indexed by multiple parameters, we need some extension of our de nitions of the fisher information and the je reys prior. Each of the. Two Parameter Normal Model.
From www.mdpi.com
Mathematics Free FullText A TwoParameter Model Properties and Two Parameter Normal Model The normal distribution has two parameters, the mean and standard deviation. This lecture shows how to apply the basic principles of bayesian inference to the problem of estimating the parameters (mean and variance) of a normal distribution. However, these curves can look. The gaussian distribution does not have just one form. When the model is indexed by multiple parameters, we. Two Parameter Normal Model.
From www.coursehero.com
[Solved] Sketch the area under the standard normal curve over the Two Parameter Normal Model Normal distributions are defined by two parameters, the mean (\(\mu\)) and the standard deviation (\(\sigma\)). The normal distribution model always describes a symmetric, unimodal, bell shaped curve. The normal distribution has two parameters, the mean and standard deviation. When the model is indexed by multiple parameters, we need some extension of our de nitions of the fisher information and the. Two Parameter Normal Model.
From www.scribbr.com
Normal Distribution Examples, Formulas, & Uses Two Parameter Normal Model Instead, the shape changes based on. Normal distributions are defined by two parameters, the mean (\(\mu\)) and the standard deviation (\(\sigma\)). However, these curves can look. When the model is indexed by multiple parameters, we need some extension of our de nitions of the fisher information and the je reys prior. The normal distribution model always describes a symmetric, unimodal,. Two Parameter Normal Model.
From medium.com
[ Archived Post ] Multivariate Gaussian distributions and entropy 3 Two Parameter Normal Model Instead, the shape changes based on. When the model is indexed by multiple parameters, we need some extension of our de nitions of the fisher information and the je reys prior. Normal distributions are defined by two parameters, the mean (\(\mu\)) and the standard deviation (\(\sigma\)). Each of the pivot variables \( z \), \( t \), and \( v. Two Parameter Normal Model.
From www.scribbr.co.uk
Normal Distribution Examples, Formulas, & Uses Two Parameter Normal Model Instead, the shape changes based on. Normal distributions are defined by two parameters, the mean (\(\mu\)) and the standard deviation (\(\sigma\)). When the model is indexed by multiple parameters, we need some extension of our de nitions of the fisher information and the je reys prior. The normal distribution has two parameters, the mean and standard deviation. The gaussian distribution. Two Parameter Normal Model.
From www.numerade.com
SOLVEDFind the principal unit normal vector to the curve at the Two Parameter Normal Model When the model is indexed by multiple parameters, we need some extension of our de nitions of the fisher information and the je reys prior. However, these curves can look. Each of the pivot variables \( z \), \( t \), and \( v \) can be used to construct confidence sets for \( (\mu, \sigma) \). The gaussian distribution. Two Parameter Normal Model.
From www.mdpi.com
Mathematics Free FullText About the Equivalence of the Latent D Two Parameter Normal Model This lecture shows how to apply the basic principles of bayesian inference to the problem of estimating the parameters (mean and variance) of a normal distribution. Normal distributions are defined by two parameters, the mean (\(\mu\)) and the standard deviation (\(\sigma\)). Instead, the shape changes based on. The gaussian distribution does not have just one form. The normal distribution model. Two Parameter Normal Model.
From www.slideserve.com
PPT The Normal Distribution PowerPoint Presentation, free download Two Parameter Normal Model However, these curves can look. Normal distributions are defined by two parameters, the mean (\(\mu\)) and the standard deviation (\(\sigma\)). The gaussian distribution does not have just one form. The normal distribution model always describes a symmetric, unimodal, bell shaped curve. Each of the pivot variables \( z \), \( t \), and \( v \) can be used to. Two Parameter Normal Model.
From www.spss-tutorials.com
Normal Distribution (Statistics) The Ultimate Guide Two Parameter Normal Model Each of the pivot variables \( z \), \( t \), and \( v \) can be used to construct confidence sets for \( (\mu, \sigma) \). The normal distribution model always describes a symmetric, unimodal, bell shaped curve. The gaussian distribution does not have just one form. However, these curves can look. When the model is indexed by multiple. Two Parameter Normal Model.
From www.researchgate.net
Verification of empirical model by twoparameter lognormal model Two Parameter Normal Model The normal distribution model always describes a symmetric, unimodal, bell shaped curve. Normal distributions are defined by two parameters, the mean (\(\mu\)) and the standard deviation (\(\sigma\)). The gaussian distribution does not have just one form. The normal distribution has two parameters, the mean and standard deviation. This lecture shows how to apply the basic principles of bayesian inference to. Two Parameter Normal Model.
From www.scribbr.com
Normal Distribution Examples, Formulas, & Uses Two Parameter Normal Model This lecture shows how to apply the basic principles of bayesian inference to the problem of estimating the parameters (mean and variance) of a normal distribution. When the model is indexed by multiple parameters, we need some extension of our de nitions of the fisher information and the je reys prior. Instead, the shape changes based on. Normal distributions are. Two Parameter Normal Model.
From www.researchgate.net
Two Parameter Logistic Model (2PLM) item characteristics ccurves (ICC Two Parameter Normal Model Instead, the shape changes based on. The normal distribution model always describes a symmetric, unimodal, bell shaped curve. However, these curves can look. Normal distributions are defined by two parameters, the mean (\(\mu\)) and the standard deviation (\(\sigma\)). This lecture shows how to apply the basic principles of bayesian inference to the problem of estimating the parameters (mean and variance). Two Parameter Normal Model.
From hai-mn.github.io
HaiBiostat Gamma Distribution an Intuitive Explanation Two Parameter Normal Model The gaussian distribution does not have just one form. When the model is indexed by multiple parameters, we need some extension of our de nitions of the fisher information and the je reys prior. Each of the pivot variables \( z \), \( t \), and \( v \) can be used to construct confidence sets for \( (\mu, \sigma). Two Parameter Normal Model.
From www.scribbr.co.uk
Normal Distribution Examples, Formulas, & Uses Two Parameter Normal Model This lecture shows how to apply the basic principles of bayesian inference to the problem of estimating the parameters (mean and variance) of a normal distribution. Normal distributions are defined by two parameters, the mean (\(\mu\)) and the standard deviation (\(\sigma\)). Each of the pivot variables \( z \), \( t \), and \( v \) can be used to. Two Parameter Normal Model.
From analystprep.com
Key Properties of the Normal distribution CFA Level 1 AnalystPrep Two Parameter Normal Model The normal distribution model always describes a symmetric, unimodal, bell shaped curve. The gaussian distribution does not have just one form. Each of the pivot variables \( z \), \( t \), and \( v \) can be used to construct confidence sets for \( (\mu, \sigma) \). The normal distribution has two parameters, the mean and standard deviation. When. Two Parameter Normal Model.
From www.mdpi.com
Mathematics Free FullText A TwoParameter Model Properties and Two Parameter Normal Model Instead, the shape changes based on. The gaussian distribution does not have just one form. When the model is indexed by multiple parameters, we need some extension of our de nitions of the fisher information and the je reys prior. Each of the pivot variables \( z \), \( t \), and \( v \) can be used to construct. Two Parameter Normal Model.
From stats.stackexchange.com
probability How does the use of linearity of normal distribution help Two Parameter Normal Model Instead, the shape changes based on. The normal distribution has two parameters, the mean and standard deviation. When the model is indexed by multiple parameters, we need some extension of our de nitions of the fisher information and the je reys prior. However, these curves can look. Normal distributions are defined by two parameters, the mean (\(\mu\)) and the standard. Two Parameter Normal Model.
From towardsdatascience.com
Lognormal Distribution A simple explanation by Maja Pavlovic Two Parameter Normal Model Normal distributions are defined by two parameters, the mean (\(\mu\)) and the standard deviation (\(\sigma\)). However, these curves can look. The normal distribution has two parameters, the mean and standard deviation. This lecture shows how to apply the basic principles of bayesian inference to the problem of estimating the parameters (mean and variance) of a normal distribution. Each of the. Two Parameter Normal Model.
From www.scribbr.com
The Standard Normal Distribution Examples, Explanations, Uses Two Parameter Normal Model However, these curves can look. This lecture shows how to apply the basic principles of bayesian inference to the problem of estimating the parameters (mean and variance) of a normal distribution. The normal distribution model always describes a symmetric, unimodal, bell shaped curve. Each of the pivot variables \( z \), \( t \), and \( v \) can be. Two Parameter Normal Model.
From www.nagwa.com
Lesson Normal Distribution Nagwa Two Parameter Normal Model Instead, the shape changes based on. The normal distribution has two parameters, the mean and standard deviation. The normal distribution model always describes a symmetric, unimodal, bell shaped curve. When the model is indexed by multiple parameters, we need some extension of our de nitions of the fisher information and the je reys prior. However, these curves can look. Normal. Two Parameter Normal Model.
From corporatefinanceinstitute.com
Normal Distribution Overview, Parameters, and Properties Two Parameter Normal Model Each of the pivot variables \( z \), \( t \), and \( v \) can be used to construct confidence sets for \( (\mu, \sigma) \). The gaussian distribution does not have just one form. Normal distributions are defined by two parameters, the mean (\(\mu\)) and the standard deviation (\(\sigma\)). The normal distribution has two parameters, the mean and. Two Parameter Normal Model.
From calcworkshop.com
Weibull & Lognormal Distribution (with 7 Examples!) Two Parameter Normal Model Each of the pivot variables \( z \), \( t \), and \( v \) can be used to construct confidence sets for \( (\mu, \sigma) \). Normal distributions are defined by two parameters, the mean (\(\mu\)) and the standard deviation (\(\sigma\)). Instead, the shape changes based on. The normal distribution has two parameters, the mean and standard deviation. The. Two Parameter Normal Model.
From www.investopedia.com
Lognormal and Normal Distribution Two Parameter Normal Model The gaussian distribution does not have just one form. However, these curves can look. This lecture shows how to apply the basic principles of bayesian inference to the problem of estimating the parameters (mean and variance) of a normal distribution. The normal distribution model always describes a symmetric, unimodal, bell shaped curve. The normal distribution has two parameters, the mean. Two Parameter Normal Model.
From calcworkshop.com
Weibull & Lognormal Distribution (with 7 Examples!) Two Parameter Normal Model Each of the pivot variables \( z \), \( t \), and \( v \) can be used to construct confidence sets for \( (\mu, \sigma) \). When the model is indexed by multiple parameters, we need some extension of our de nitions of the fisher information and the je reys prior. The gaussian distribution does not have just one. Two Parameter Normal Model.
From www.scribbr.com
Normal Distribution Examples, Formulas, & Uses Two Parameter Normal Model However, these curves can look. Instead, the shape changes based on. This lecture shows how to apply the basic principles of bayesian inference to the problem of estimating the parameters (mean and variance) of a normal distribution. Each of the pivot variables \( z \), \( t \), and \( v \) can be used to construct confidence sets for. Two Parameter Normal Model.
From www.researchgate.net
Twoparameter logistic model item response functions for four Two Parameter Normal Model The gaussian distribution does not have just one form. Instead, the shape changes based on. This lecture shows how to apply the basic principles of bayesian inference to the problem of estimating the parameters (mean and variance) of a normal distribution. Each of the pivot variables \( z \), \( t \), and \( v \) can be used to. Two Parameter Normal Model.
From www.slideserve.com
PPT Introduction Rasch User’s Group PowerPoint Presentation, free Two Parameter Normal Model The normal distribution has two parameters, the mean and standard deviation. The normal distribution model always describes a symmetric, unimodal, bell shaped curve. Each of the pivot variables \( z \), \( t \), and \( v \) can be used to construct confidence sets for \( (\mu, \sigma) \). When the model is indexed by multiple parameters, we need. Two Parameter Normal Model.
From www.researchgate.net
Item response functions from the twoparameter logistic model. Item Two Parameter Normal Model The gaussian distribution does not have just one form. This lecture shows how to apply the basic principles of bayesian inference to the problem of estimating the parameters (mean and variance) of a normal distribution. The normal distribution has two parameters, the mean and standard deviation. Each of the pivot variables \( z \), \( t \), and \( v. Two Parameter Normal Model.
From www.youtube.com
10分鐘介紹Twoparameter Logistic Model YouTube Two Parameter Normal Model The normal distribution model always describes a symmetric, unimodal, bell shaped curve. Each of the pivot variables \( z \), \( t \), and \( v \) can be used to construct confidence sets for \( (\mu, \sigma) \). This lecture shows how to apply the basic principles of bayesian inference to the problem of estimating the parameters (mean and. Two Parameter Normal Model.
From www.qualitygurus.com
Two Parameters Weibull Distribution Quality Gurus Two Parameter Normal Model The normal distribution has two parameters, the mean and standard deviation. The gaussian distribution does not have just one form. Normal distributions are defined by two parameters, the mean (\(\mu\)) and the standard deviation (\(\sigma\)). When the model is indexed by multiple parameters, we need some extension of our de nitions of the fisher information and the je reys prior.. Two Parameter Normal Model.
From www.scribbr.com
The Standard Normal Distribution Calculator, Examples & Uses Two Parameter Normal Model The gaussian distribution does not have just one form. This lecture shows how to apply the basic principles of bayesian inference to the problem of estimating the parameters (mean and variance) of a normal distribution. The normal distribution has two parameters, the mean and standard deviation. Normal distributions are defined by two parameters, the mean (\(\mu\)) and the standard deviation. Two Parameter Normal Model.
From www.numerade.com
SOLVEDFind the principal unit normal vector to the curve at the Two Parameter Normal Model The gaussian distribution does not have just one form. Instead, the shape changes based on. However, these curves can look. The normal distribution has two parameters, the mean and standard deviation. The normal distribution model always describes a symmetric, unimodal, bell shaped curve. This lecture shows how to apply the basic principles of bayesian inference to the problem of estimating. Two Parameter Normal Model.