Undamped Oscillation Differential Equation . undamped oscillations are used. First let us consider undamped \(c = 0\) motion for simplicity. We have the equation \[ mx'' + kx = f_0 \cos (\omega t) \nonumber \] this equation has the complementary solution (solution to the associated homogeneous equation) \[x_c = c_1 \cos ( \omega_0t) + c_2 \sin (\omega_0t) \nonumber \] This is the simplest case that we can consider. −1/2 ± i √ 11/2. Free or unforced vibrations means that \(f(t) = 0\) and. In general, for free undamped motion, a solution of the. S2 + s + 3 = 0. \(x_{max}\)), and the phase \(\phi\) describes how the. many systems are underdamped, and oscillate while the amplitude decreases exponentially, such as the mass oscillating on a spring. We are assuming that things like air resistance and friction are negligible. the amplitude \(c\) describes the maximum displacement during the oscillations (i.e. undamped forced motion and resonance. free, undamped vibrations. E−t/2 cos(√ 11 t/2), e−t/2.
from www.numerade.com
many systems are underdamped, and oscillate while the amplitude decreases exponentially, such as the mass oscillating on a spring. We have the equation \[ mx'' + kx = f_0 \cos (\omega t) \nonumber \] this equation has the complementary solution (solution to the associated homogeneous equation) \[x_c = c_1 \cos ( \omega_0t) + c_2 \sin (\omega_0t) \nonumber \] one of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity. undamped oscillations are used. \(x_{max}\)), and the phase \(\phi\) describes how the. free, undamped vibrations. undamped forced motion and resonance. S2 + s + 3 = 0. This is the simplest case that we can consider. In general, for free undamped motion, a solution of the.
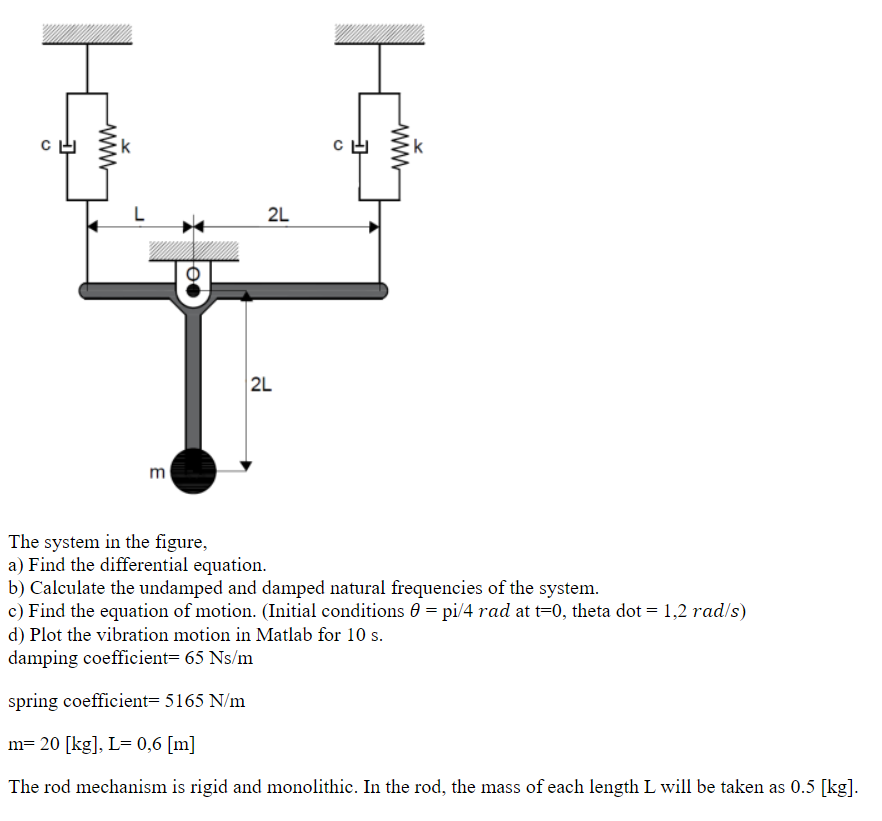
SOLVED The system in the figure, a) Find the differential equation. b
Undamped Oscillation Differential Equation the amplitude \(c\) describes the maximum displacement during the oscillations (i.e. Free or unforced vibrations means that \(f(t) = 0\) and. undamped oscillations are used. many systems are underdamped, and oscillate while the amplitude decreases exponentially, such as the mass oscillating on a spring. In general, for free undamped motion, a solution of the. Since m and k are. free, undamped vibrations. We are assuming that things like air resistance and friction are negligible. First let us consider undamped \(c = 0\) motion for simplicity. −1/2 ± i √ 11/2. We have the equation \[ mx'' + kx = f_0 \cos (\omega t) \nonumber \] this equation has the complementary solution (solution to the associated homogeneous equation) \[x_c = c_1 \cos ( \omega_0t) + c_2 \sin (\omega_0t) \nonumber \] \(x_{max}\)), and the phase \(\phi\) describes how the. This is the simplest case that we can consider. one of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity. S2 + s + 3 = 0. the amplitude \(c\) describes the maximum displacement during the oscillations (i.e.
From www.houseofmath.com
The Differential Equation for Harmonic Oscillators Undamped Oscillation Differential Equation the amplitude \(c\) describes the maximum displacement during the oscillations (i.e. First let us consider undamped \(c = 0\) motion for simplicity. Free or unforced vibrations means that \(f(t) = 0\) and. Since m and k are. We have the equation \[ mx'' + kx = f_0 \cos (\omega t) \nonumber \] this equation has the complementary solution (solution. Undamped Oscillation Differential Equation.
From www.chegg.com
Solved a) The differential equation of an undamped free Undamped Oscillation Differential Equation E−t/2 cos(√ 11 t/2), e−t/2. S2 + s + 3 = 0. one of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity. Since m and k are. First let us consider undamped \(c = 0\) motion for simplicity. the amplitude \(c\) describes the maximum displacement during the oscillations (i.e.. Undamped Oscillation Differential Equation.
From www.chegg.com
Solved 1. Consider an undamped simple harmonic oscillator Undamped Oscillation Differential Equation This is the simplest case that we can consider. In general, for free undamped motion, a solution of the. undamped forced motion and resonance. free, undamped vibrations. We have the equation \[ mx'' + kx = f_0 \cos (\omega t) \nonumber \] this equation has the complementary solution (solution to the associated homogeneous equation) \[x_c = c_1 \cos. Undamped Oscillation Differential Equation.
From www.numerade.com
SOLVEDThe differential equation of motion of an undamped system is Undamped Oscillation Differential Equation This is the simplest case that we can consider. many systems are underdamped, and oscillate while the amplitude decreases exponentially, such as the mass oscillating on a spring. Since m and k are. E−t/2 cos(√ 11 t/2), e−t/2. Free or unforced vibrations means that \(f(t) = 0\) and. undamped forced motion and resonance. one of the most. Undamped Oscillation Differential Equation.
From www.chegg.com
Solved A.1.1. Undamped Vibration (a) Differential equation Undamped Oscillation Differential Equation free, undamped vibrations. Since m and k are. −1/2 ± i √ 11/2. the amplitude \(c\) describes the maximum displacement during the oscillations (i.e. We are assuming that things like air resistance and friction are negligible. First let us consider undamped \(c = 0\) motion for simplicity. S2 + s + 3 = 0. This is the simplest. Undamped Oscillation Differential Equation.
From www.youtube.com
Differential Equations Free Undamped Vibration YouTube Undamped Oscillation Differential Equation E−t/2 cos(√ 11 t/2), e−t/2. First let us consider undamped \(c = 0\) motion for simplicity. This is the simplest case that we can consider. \(x_{max}\)), and the phase \(\phi\) describes how the. the amplitude \(c\) describes the maximum displacement during the oscillations (i.e. In general, for free undamped motion, a solution of the. S2 + s + 3. Undamped Oscillation Differential Equation.
From www.youtube.com
Differential Equations Intro Video Undamped Forced Oscillators Undamped Oscillation Differential Equation undamped forced motion and resonance. Since m and k are. the amplitude \(c\) describes the maximum displacement during the oscillations (i.e. \(x_{max}\)), and the phase \(\phi\) describes how the. many systems are underdamped, and oscillate while the amplitude decreases exponentially, such as the mass oscillating on a spring. We have the equation \[ mx'' + kx =. Undamped Oscillation Differential Equation.
From www.chegg.com
Solved (b) Determine the response of an undamped oscillator Undamped Oscillation Differential Equation −1/2 ± i √ 11/2. This is the simplest case that we can consider. We are assuming that things like air resistance and friction are negligible. \(x_{max}\)), and the phase \(\phi\) describes how the. the amplitude \(c\) describes the maximum displacement during the oscillations (i.e. Since m and k are. free, undamped vibrations. undamped forced motion and. Undamped Oscillation Differential Equation.
From www.youtube.com
M308 Differential Equations Undamped Forced Vibrations YouTube Undamped Oscillation Differential Equation the amplitude \(c\) describes the maximum displacement during the oscillations (i.e. Free or unforced vibrations means that \(f(t) = 0\) and. E−t/2 cos(√ 11 t/2), e−t/2. Since m and k are. \(x_{max}\)), and the phase \(\phi\) describes how the. In general, for free undamped motion, a solution of the. free, undamped vibrations. −1/2 ± i √ 11/2. We. Undamped Oscillation Differential Equation.
From present5.com
FREE UNDAMPED OSCILLATIONS Oscillation system is Undamped Oscillation Differential Equation Since m and k are. We are assuming that things like air resistance and friction are negligible. free, undamped vibrations. −1/2 ± i √ 11/2. \(x_{max}\)), and the phase \(\phi\) describes how the. S2 + s + 3 = 0. E−t/2 cos(√ 11 t/2), e−t/2. This is the simplest case that we can consider. undamped forced motion and. Undamped Oscillation Differential Equation.
From www.reddit.com
How do you get this solution to the simple harmonic oscillator Undamped Oscillation Differential Equation E−t/2 cos(√ 11 t/2), e−t/2. many systems are underdamped, and oscillate while the amplitude decreases exponentially, such as the mass oscillating on a spring. We are assuming that things like air resistance and friction are negligible. \(x_{max}\)), and the phase \(\phi\) describes how the. the amplitude \(c\) describes the maximum displacement during the oscillations (i.e. This is the. Undamped Oscillation Differential Equation.
From www.chegg.com
Solved A model of the free, undamped oscillations of a mass Undamped Oscillation Differential Equation \(x_{max}\)), and the phase \(\phi\) describes how the. free, undamped vibrations. undamped forced motion and resonance. We are assuming that things like air resistance and friction are negligible. In general, for free undamped motion, a solution of the. S2 + s + 3 = 0. undamped oscillations are used. Since m and k are. This is the. Undamped Oscillation Differential Equation.
From www.chegg.com
Solved 2. The damped harmonic oscillator equation takes the Undamped Oscillation Differential Equation −1/2 ± i √ 11/2. We are assuming that things like air resistance and friction are negligible. one of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity. In general, for free undamped motion, a solution of the. undamped oscillations are used. many systems are underdamped, and oscillate while. Undamped Oscillation Differential Equation.
From www.youtube.com
Video321 Springmass system; undamped free oscillation. Elementary Undamped Oscillation Differential Equation undamped oscillations are used. the amplitude \(c\) describes the maximum displacement during the oscillations (i.e. First let us consider undamped \(c = 0\) motion for simplicity. This is the simplest case that we can consider. Since m and k are. −1/2 ± i √ 11/2. E−t/2 cos(√ 11 t/2), e−t/2. \(x_{max}\)), and the phase \(\phi\) describes how the.. Undamped Oscillation Differential Equation.
From www.youtube.com
Differential Equations Forced Oscillation Beats YouTube Undamped Oscillation Differential Equation undamped forced motion and resonance. We have the equation \[ mx'' + kx = f_0 \cos (\omega t) \nonumber \] this equation has the complementary solution (solution to the associated homogeneous equation) \[x_c = c_1 \cos ( \omega_0t) + c_2 \sin (\omega_0t) \nonumber \] Free or unforced vibrations means that \(f(t) = 0\) and. We are assuming that things. Undamped Oscillation Differential Equation.
From www.slideserve.com
PPT Chapter 13 Oscillatory Motions PowerPoint Presentation, free Undamped Oscillation Differential Equation one of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity. This is the simplest case that we can consider. \(x_{max}\)), and the phase \(\phi\) describes how the. S2 + s + 3 = 0. −1/2 ± i √ 11/2. We have the equation \[ mx'' + kx = f_0 \cos. Undamped Oscillation Differential Equation.
From www.numerade.com
SOLVED The system in the figure, a) Find the differential equation. b Undamped Oscillation Differential Equation In general, for free undamped motion, a solution of the. E−t/2 cos(√ 11 t/2), e−t/2. free, undamped vibrations. Since m and k are. Free or unforced vibrations means that \(f(t) = 0\) and. S2 + s + 3 = 0. First let us consider undamped \(c = 0\) motion for simplicity. −1/2 ± i √ 11/2. many systems. Undamped Oscillation Differential Equation.
From www.chegg.com
Solved The differential equation for an undamped vibration Undamped Oscillation Differential Equation S2 + s + 3 = 0. free, undamped vibrations. First let us consider undamped \(c = 0\) motion for simplicity. This is the simplest case that we can consider. E−t/2 cos(√ 11 t/2), e−t/2. We are assuming that things like air resistance and friction are negligible. the amplitude \(c\) describes the maximum displacement during the oscillations (i.e.. Undamped Oscillation Differential Equation.
From www.numerade.com
SOLVED Laplace Transforms Damped Oscillator A damped simple harmonic Undamped Oscillation Differential Equation This is the simplest case that we can consider. \(x_{max}\)), and the phase \(\phi\) describes how the. E−t/2 cos(√ 11 t/2), e−t/2. the amplitude \(c\) describes the maximum displacement during the oscillations (i.e. undamped forced motion and resonance. S2 + s + 3 = 0. undamped oscillations are used. many systems are underdamped, and oscillate while. Undamped Oscillation Differential Equation.
From www.chegg.com
Solved 5. Consider the undamped oscillator differential Undamped Oscillation Differential Equation many systems are underdamped, and oscillate while the amplitude decreases exponentially, such as the mass oscillating on a spring. First let us consider undamped \(c = 0\) motion for simplicity. \(x_{max}\)), and the phase \(\phi\) describes how the. undamped forced motion and resonance. free, undamped vibrations. S2 + s + 3 = 0. In general, for free. Undamped Oscillation Differential Equation.
From www.numerade.com
SOLVED Consider the secondorder differential equation for a simple Undamped Oscillation Differential Equation In general, for free undamped motion, a solution of the. Free or unforced vibrations means that \(f(t) = 0\) and. \(x_{max}\)), and the phase \(\phi\) describes how the. We are assuming that things like air resistance and friction are negligible. Since m and k are. First let us consider undamped \(c = 0\) motion for simplicity. the amplitude \(c\). Undamped Oscillation Differential Equation.
From www.chegg.com
Solved d2x +kx F sin ot governs the motion of an undamped Undamped Oscillation Differential Equation free, undamped vibrations. We have the equation \[ mx'' + kx = f_0 \cos (\omega t) \nonumber \] this equation has the complementary solution (solution to the associated homogeneous equation) \[x_c = c_1 \cos ( \omega_0t) + c_2 \sin (\omega_0t) \nonumber \] Free or unforced vibrations means that \(f(t) = 0\) and. This is the simplest case that we. Undamped Oscillation Differential Equation.
From www.numerade.com
SOLVED The differential equation of a damped harmonic oscillator is Undamped Oscillation Differential Equation \(x_{max}\)), and the phase \(\phi\) describes how the. We are assuming that things like air resistance and friction are negligible. the amplitude \(c\) describes the maximum displacement during the oscillations (i.e. In general, for free undamped motion, a solution of the. one of the most important examples of periodic motion is simple harmonic motion (shm), in which some. Undamped Oscillation Differential Equation.
From www.youtube.com
Ex 1 Free Undamped Motion IVP Problem (Spring System) Differential Undamped Oscillation Differential Equation Free or unforced vibrations means that \(f(t) = 0\) and. Since m and k are. We are assuming that things like air resistance and friction are negligible. E−t/2 cos(√ 11 t/2), e−t/2. one of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity. This is the simplest case that we can. Undamped Oscillation Differential Equation.
From www.coursehero.com
[Solved] This is an example of an Undamped Forced Oscillation where the Undamped Oscillation Differential Equation \(x_{max}\)), and the phase \(\phi\) describes how the. We have the equation \[ mx'' + kx = f_0 \cos (\omega t) \nonumber \] this equation has the complementary solution (solution to the associated homogeneous equation) \[x_c = c_1 \cos ( \omega_0t) + c_2 \sin (\omega_0t) \nonumber \] Free or unforced vibrations means that \(f(t) = 0\) and. In general, for. Undamped Oscillation Differential Equation.
From www.numerade.com
SOLVEDAn undamped driven harmonic oscillator satisfies the equation of Undamped Oscillation Differential Equation We have the equation \[ mx'' + kx = f_0 \cos (\omega t) \nonumber \] this equation has the complementary solution (solution to the associated homogeneous equation) \[x_c = c_1 \cos ( \omega_0t) + c_2 \sin (\omega_0t) \nonumber \] Since m and k are. one of the most important examples of periodic motion is simple harmonic motion (shm), in. Undamped Oscillation Differential Equation.
From present5.com
FREE UNDAMPED OSCILLATIONS The charge current and Undamped Oscillation Differential Equation Free or unforced vibrations means that \(f(t) = 0\) and. E−t/2 cos(√ 11 t/2), e−t/2. many systems are underdamped, and oscillate while the amplitude decreases exponentially, such as the mass oscillating on a spring. \(x_{max}\)), and the phase \(\phi\) describes how the. −1/2 ± i √ 11/2. undamped forced motion and resonance. S2 + s + 3 =. Undamped Oscillation Differential Equation.
From exyndioyy.blob.core.windows.net
Oscillation Amplitude Equation at Jill Sneed blog Undamped Oscillation Differential Equation \(x_{max}\)), and the phase \(\phi\) describes how the. Free or unforced vibrations means that \(f(t) = 0\) and. undamped oscillations are used. Since m and k are. This is the simplest case that we can consider. many systems are underdamped, and oscillate while the amplitude decreases exponentially, such as the mass oscillating on a spring. We are assuming. Undamped Oscillation Differential Equation.
From www.youtube.com
Intro to MassSpring Oscillator (SecondOrder Differential Equation Undamped Oscillation Differential Equation Since m and k are. This is the simplest case that we can consider. −1/2 ± i √ 11/2. We have the equation \[ mx'' + kx = f_0 \cos (\omega t) \nonumber \] this equation has the complementary solution (solution to the associated homogeneous equation) \[x_c = c_1 \cos ( \omega_0t) + c_2 \sin (\omega_0t) \nonumber \] the. Undamped Oscillation Differential Equation.
From www.chegg.com
Solved 2. The differential equation for an undamped Undamped Oscillation Differential Equation the amplitude \(c\) describes the maximum displacement during the oscillations (i.e. \(x_{max}\)), and the phase \(\phi\) describes how the. undamped forced motion and resonance. We have the equation \[ mx'' + kx = f_0 \cos (\omega t) \nonumber \] this equation has the complementary solution (solution to the associated homogeneous equation) \[x_c = c_1 \cos ( \omega_0t) +. Undamped Oscillation Differential Equation.
From www.scribd.com
Free Undamped SDOFpart 1 PDF Download Free PDF Oscillation Undamped Oscillation Differential Equation E−t/2 cos(√ 11 t/2), e−t/2. \(x_{max}\)), and the phase \(\phi\) describes how the. In general, for free undamped motion, a solution of the. This is the simplest case that we can consider. −1/2 ± i √ 11/2. Free or unforced vibrations means that \(f(t) = 0\) and. undamped oscillations are used. First let us consider undamped \(c = 0\). Undamped Oscillation Differential Equation.
From www.youtube.com
Undamped Free Vibration (Simple Harmonic Motion) Differential Undamped Oscillation Differential Equation undamped oscillations are used. We have the equation \[ mx'' + kx = f_0 \cos (\omega t) \nonumber \] this equation has the complementary solution (solution to the associated homogeneous equation) \[x_c = c_1 \cos ( \omega_0t) + c_2 \sin (\omega_0t) \nonumber \] S2 + s + 3 = 0. First let us consider undamped \(c = 0\) motion. Undamped Oscillation Differential Equation.
From www.youtube.com
Undamped Forced Vibration Lecture YouTube Undamped Oscillation Differential Equation \(x_{max}\)), and the phase \(\phi\) describes how the. the amplitude \(c\) describes the maximum displacement during the oscillations (i.e. This is the simplest case that we can consider. We have the equation \[ mx'' + kx = f_0 \cos (\omega t) \nonumber \] this equation has the complementary solution (solution to the associated homogeneous equation) \[x_c = c_1 \cos. Undamped Oscillation Differential Equation.
From www.youtube.com
Ex 3 Free Undamped Motion IVP Problem Spring System Differential Undamped Oscillation Differential Equation E−t/2 cos(√ 11 t/2), e−t/2. Free or unforced vibrations means that \(f(t) = 0\) and. the amplitude \(c\) describes the maximum displacement during the oscillations (i.e. First let us consider undamped \(c = 0\) motion for simplicity. We are assuming that things like air resistance and friction are negligible. free, undamped vibrations. Since m and k are. . Undamped Oscillation Differential Equation.
From www.coursehero.com
[Solved] Derive the Equation of motion for undamped single degree of Undamped Oscillation Differential Equation This is the simplest case that we can consider. First let us consider undamped \(c = 0\) motion for simplicity. one of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity. −1/2 ± i √ 11/2. \(x_{max}\)), and the phase \(\phi\) describes how the. In general, for free undamped motion, a. Undamped Oscillation Differential Equation.