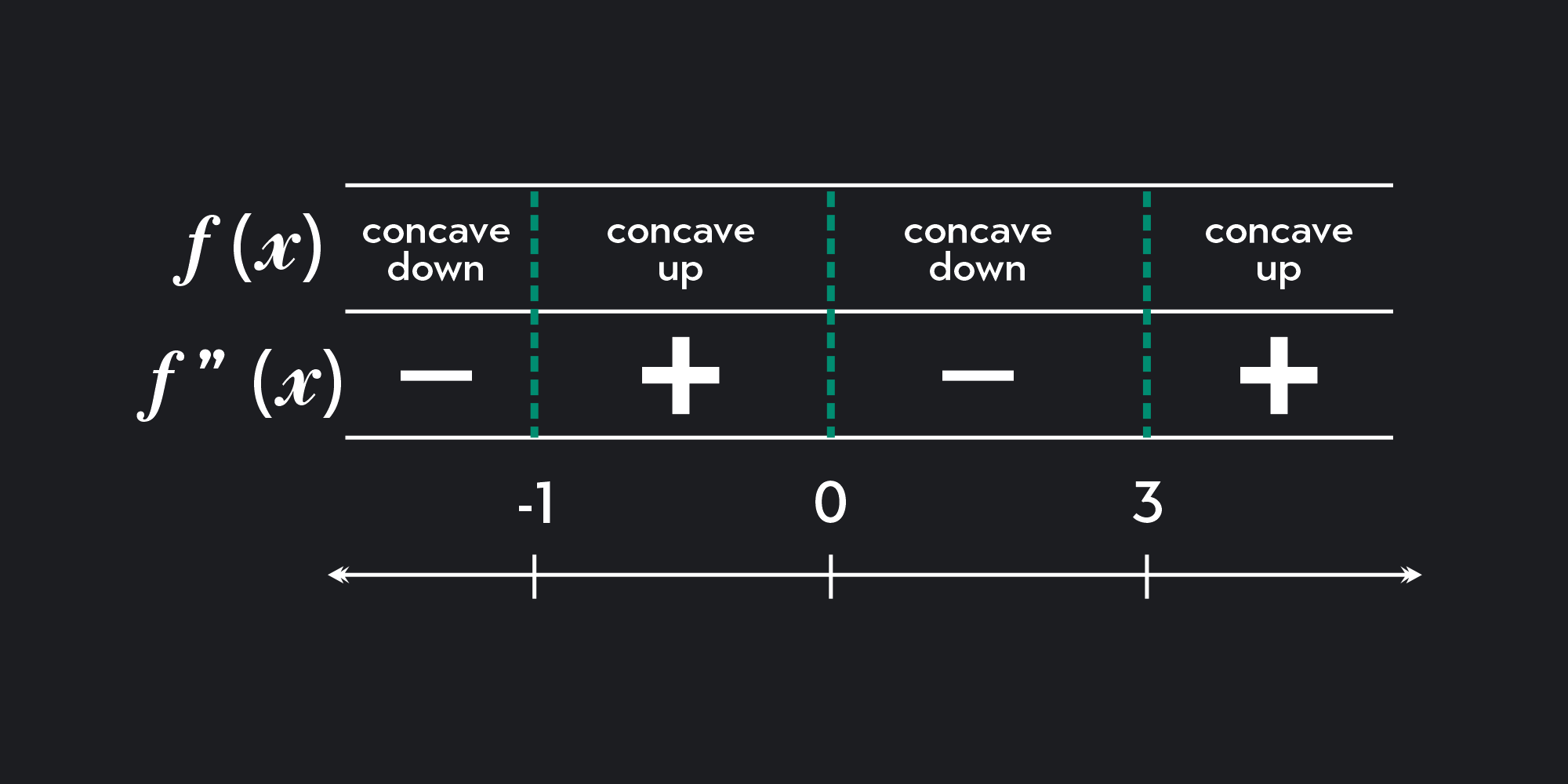
Point Of Inflection Third Derivative . Calculate the value of the function at the x value for the point of. What is a point of inflection? Decide whether you have a minimum/maximum or a point of inflection. An inflection point is where a curve changes from concave to convex or vice versa. When the second derivative is negative, the function is concave downward. There are two types of inflection points: Use concavity and inflection points to explain how the sign of the second derivative affects the shape of a function’s graph. When the sign of the first derivative (ie of the gradient) is the same on both. And the inflection point is where it goes from concave upward to concave downward (or vice versa). Explain the concavity test for a function over an open interval. Given a curve y=f(x), a point of inflection is a point at which the second derivative equals to zero, f''(x)=0, and across which the second derivative. At as level you encountered points of inflection when discussing stationary points.
from articles.outlier.org
Decide whether you have a minimum/maximum or a point of inflection. At as level you encountered points of inflection when discussing stationary points. What is a point of inflection? Use concavity and inflection points to explain how the sign of the second derivative affects the shape of a function’s graph. And the inflection point is where it goes from concave upward to concave downward (or vice versa). There are two types of inflection points: When the second derivative is negative, the function is concave downward. When the sign of the first derivative (ie of the gradient) is the same on both. An inflection point is where a curve changes from concave to convex or vice versa. Calculate the value of the function at the x value for the point of.
Inflection Point Definition and How to Find It in 5 Steps Outlier
Point Of Inflection Third Derivative And the inflection point is where it goes from concave upward to concave downward (or vice versa). There are two types of inflection points: Explain the concavity test for a function over an open interval. Use concavity and inflection points to explain how the sign of the second derivative affects the shape of a function’s graph. Decide whether you have a minimum/maximum or a point of inflection. Given a curve y=f(x), a point of inflection is a point at which the second derivative equals to zero, f''(x)=0, and across which the second derivative. And the inflection point is where it goes from concave upward to concave downward (or vice versa). Calculate the value of the function at the x value for the point of. At as level you encountered points of inflection when discussing stationary points. An inflection point is where a curve changes from concave to convex or vice versa. When the sign of the first derivative (ie of the gradient) is the same on both. When the second derivative is negative, the function is concave downward. What is a point of inflection?
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Point Of Inflection Third Derivative An inflection point is where a curve changes from concave to convex or vice versa. Given a curve y=f(x), a point of inflection is a point at which the second derivative equals to zero, f''(x)=0, and across which the second derivative. When the second derivative is negative, the function is concave downward. Calculate the value of the function at the. Point Of Inflection Third Derivative.
From www.savemyexams.com
Concavity & Points of Inflection DP IB Maths AA HL Revision Notes 2021 Point Of Inflection Third Derivative When the sign of the first derivative (ie of the gradient) is the same on both. Given a curve y=f(x), a point of inflection is a point at which the second derivative equals to zero, f''(x)=0, and across which the second derivative. What is a point of inflection? And the inflection point is where it goes from concave upward to. Point Of Inflection Third Derivative.
From www.youtube.com
Inflection points from graphs of function & derivatives AP Calculus Point Of Inflection Third Derivative And the inflection point is where it goes from concave upward to concave downward (or vice versa). Calculate the value of the function at the x value for the point of. Explain the concavity test for a function over an open interval. An inflection point is where a curve changes from concave to convex or vice versa. Given a curve. Point Of Inflection Third Derivative.
From www.chegg.com
Solved Find the equation of the curve whose third derivative Point Of Inflection Third Derivative Calculate the value of the function at the x value for the point of. What is a point of inflection? An inflection point is where a curve changes from concave to convex or vice versa. Use concavity and inflection points to explain how the sign of the second derivative affects the shape of a function’s graph. There are two types. Point Of Inflection Third Derivative.
From en.wikipedia.org
Inflection point Wikipedia Point Of Inflection Third Derivative Calculate the value of the function at the x value for the point of. Decide whether you have a minimum/maximum or a point of inflection. Explain the concavity test for a function over an open interval. Given a curve y=f(x), a point of inflection is a point at which the second derivative equals to zero, f''(x)=0, and across which the. Point Of Inflection Third Derivative.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Point Of Inflection Third Derivative An inflection point is where a curve changes from concave to convex or vice versa. Calculate the value of the function at the x value for the point of. There are two types of inflection points: Explain the concavity test for a function over an open interval. Given a curve y=f(x), a point of inflection is a point at which. Point Of Inflection Third Derivative.
From www.wikihow.com
5 Ways to Find Inflection Points wikiHow Point Of Inflection Third Derivative Decide whether you have a minimum/maximum or a point of inflection. At as level you encountered points of inflection when discussing stationary points. Use concavity and inflection points to explain how the sign of the second derivative affects the shape of a function’s graph. When the second derivative is negative, the function is concave downward. Explain the concavity test for. Point Of Inflection Third Derivative.
From www.nagwa.com
Question Video Finding the Inflection Point of a Function Using the Point Of Inflection Third Derivative Decide whether you have a minimum/maximum or a point of inflection. An inflection point is where a curve changes from concave to convex or vice versa. And the inflection point is where it goes from concave upward to concave downward (or vice versa). At as level you encountered points of inflection when discussing stationary points. What is a point of. Point Of Inflection Third Derivative.
From mathemerize.com
What is the Point of Inflection ? Mathemerize Point Of Inflection Third Derivative And the inflection point is where it goes from concave upward to concave downward (or vice versa). Given a curve y=f(x), a point of inflection is a point at which the second derivative equals to zero, f''(x)=0, and across which the second derivative. Decide whether you have a minimum/maximum or a point of inflection. An inflection point is where a. Point Of Inflection Third Derivative.
From mungfali.com
Question Video Finding The 푥coordinates Of The Inflection Points Of A 168 Point Of Inflection Third Derivative And the inflection point is where it goes from concave upward to concave downward (or vice versa). What is a point of inflection? When the second derivative is negative, the function is concave downward. Explain the concavity test for a function over an open interval. An inflection point is where a curve changes from concave to convex or vice versa.. Point Of Inflection Third Derivative.
From www.showme.com
Points of inflection Math, Calculus, Derivatives and Differentiation Point Of Inflection Third Derivative Use concavity and inflection points to explain how the sign of the second derivative affects the shape of a function’s graph. Decide whether you have a minimum/maximum or a point of inflection. At as level you encountered points of inflection when discussing stationary points. Explain the concavity test for a function over an open interval. When the sign of the. Point Of Inflection Third Derivative.
From www.youtube.com
Find inflection point of 3rd degree polynomial function by using the Point Of Inflection Third Derivative Given a curve y=f(x), a point of inflection is a point at which the second derivative equals to zero, f''(x)=0, and across which the second derivative. And the inflection point is where it goes from concave upward to concave downward (or vice versa). Decide whether you have a minimum/maximum or a point of inflection. At as level you encountered points. Point Of Inflection Third Derivative.
From www.savemyexams.com
Points of Inflection OCR A Level Maths Pure Revision Notes 2018 Point Of Inflection Third Derivative When the second derivative is negative, the function is concave downward. Decide whether you have a minimum/maximum or a point of inflection. Calculate the value of the function at the x value for the point of. When the sign of the first derivative (ie of the gradient) is the same on both. At as level you encountered points of inflection. Point Of Inflection Third Derivative.
From www.youtube.com
finding third derivative YouTube Point Of Inflection Third Derivative Explain the concavity test for a function over an open interval. Given a curve y=f(x), a point of inflection is a point at which the second derivative equals to zero, f''(x)=0, and across which the second derivative. At as level you encountered points of inflection when discussing stationary points. There are two types of inflection points: When the second derivative. Point Of Inflection Third Derivative.
From www.nagwa.com
Question Video Finding the Inflection Points of a Polynomial Function Point Of Inflection Third Derivative At as level you encountered points of inflection when discussing stationary points. When the sign of the first derivative (ie of the gradient) is the same on both. And the inflection point is where it goes from concave upward to concave downward (or vice versa). An inflection point is where a curve changes from concave to convex or vice versa.. Point Of Inflection Third Derivative.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Point Of Inflection Third Derivative When the sign of the first derivative (ie of the gradient) is the same on both. Use concavity and inflection points to explain how the sign of the second derivative affects the shape of a function’s graph. Decide whether you have a minimum/maximum or a point of inflection. There are two types of inflection points: What is a point of. Point Of Inflection Third Derivative.
From www.youtube.com
Differentiation of Parametric Curves Finding The Third Derivative Point Of Inflection Third Derivative When the second derivative is negative, the function is concave downward. There are two types of inflection points: What is a point of inflection? At as level you encountered points of inflection when discussing stationary points. Explain the concavity test for a function over an open interval. Use concavity and inflection points to explain how the sign of the second. Point Of Inflection Third Derivative.
From www.nagwa.com
Question Video Finding the Inflection Point of the Curve of a Point Of Inflection Third Derivative Calculate the value of the function at the x value for the point of. At as level you encountered points of inflection when discussing stationary points. What is a point of inflection? There are two types of inflection points: When the sign of the first derivative (ie of the gradient) is the same on both. Decide whether you have a. Point Of Inflection Third Derivative.
From slideplayer.com
Derivatives in Action Chapter ppt download Point Of Inflection Third Derivative And the inflection point is where it goes from concave upward to concave downward (or vice versa). Given a curve y=f(x), a point of inflection is a point at which the second derivative equals to zero, f''(x)=0, and across which the second derivative. When the second derivative is negative, the function is concave downward. Decide whether you have a minimum/maximum. Point Of Inflection Third Derivative.
From www.vrogue.co
Inflection Point Definition And How To Find It In 5 S vrogue.co Point Of Inflection Third Derivative Given a curve y=f(x), a point of inflection is a point at which the second derivative equals to zero, f''(x)=0, and across which the second derivative. There are two types of inflection points: Explain the concavity test for a function over an open interval. And the inflection point is where it goes from concave upward to concave downward (or vice. Point Of Inflection Third Derivative.
From www.radfordmathematics.com
Point of Inflection Calculus Point Of Inflection Third Derivative At as level you encountered points of inflection when discussing stationary points. What is a point of inflection? An inflection point is where a curve changes from concave to convex or vice versa. Calculate the value of the function at the x value for the point of. When the second derivative is negative, the function is concave downward. And the. Point Of Inflection Third Derivative.
From en.neurochispas.com
Points of inflection of a function Formulas and Exercises Neurochispas Point Of Inflection Third Derivative Given a curve y=f(x), a point of inflection is a point at which the second derivative equals to zero, f''(x)=0, and across which the second derivative. Use concavity and inflection points to explain how the sign of the second derivative affects the shape of a function’s graph. There are two types of inflection points: When the second derivative is negative,. Point Of Inflection Third Derivative.
From www.wikihow.com
How to Find Inflection Points 6 Simple & Easy to Follow Steps Point Of Inflection Third Derivative When the sign of the first derivative (ie of the gradient) is the same on both. At as level you encountered points of inflection when discussing stationary points. An inflection point is where a curve changes from concave to convex or vice versa. And the inflection point is where it goes from concave upward to concave downward (or vice versa).. Point Of Inflection Third Derivative.
From www.radfordmathematics.com
Point of Inflection Calculus Point Of Inflection Third Derivative When the sign of the first derivative (ie of the gradient) is the same on both. There are two types of inflection points: And the inflection point is where it goes from concave upward to concave downward (or vice versa). What is a point of inflection? Calculate the value of the function at the x value for the point of.. Point Of Inflection Third Derivative.
From study.com
Finding Inflection Points and Concavity Overview & Examples Lesson Point Of Inflection Third Derivative When the sign of the first derivative (ie of the gradient) is the same on both. And the inflection point is where it goes from concave upward to concave downward (or vice versa). At as level you encountered points of inflection when discussing stationary points. Use concavity and inflection points to explain how the sign of the second derivative affects. Point Of Inflection Third Derivative.
From www.nagwa.com
Question Video Finding the Inflection Point of a Function Nagwa Point Of Inflection Third Derivative Explain the concavity test for a function over an open interval. Calculate the value of the function at the x value for the point of. When the second derivative is negative, the function is concave downward. At as level you encountered points of inflection when discussing stationary points. Given a curve y=f(x), a point of inflection is a point at. Point Of Inflection Third Derivative.
From www.storyofmathematics.com
Inflection Points Calculator + Online Solver With Free Steps Point Of Inflection Third Derivative Decide whether you have a minimum/maximum or a point of inflection. At as level you encountered points of inflection when discussing stationary points. What is a point of inflection? Explain the concavity test for a function over an open interval. There are two types of inflection points: Calculate the value of the function at the x value for the point. Point Of Inflection Third Derivative.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Point Of Inflection Third Derivative What is a point of inflection? Given a curve y=f(x), a point of inflection is a point at which the second derivative equals to zero, f''(x)=0, and across which the second derivative. When the sign of the first derivative (ie of the gradient) is the same on both. When the second derivative is negative, the function is concave downward. Decide. Point Of Inflection Third Derivative.
From copyprogramming.com
Inflection point, understanding problem Point Of Inflection Third Derivative Given a curve y=f(x), a point of inflection is a point at which the second derivative equals to zero, f''(x)=0, and across which the second derivative. When the sign of the first derivative (ie of the gradient) is the same on both. At as level you encountered points of inflection when discussing stationary points. What is a point of inflection?. Point Of Inflection Third Derivative.
From www.radfordmathematics.com
Point of Inflection Calculus Point Of Inflection Third Derivative Decide whether you have a minimum/maximum or a point of inflection. When the second derivative is negative, the function is concave downward. And the inflection point is where it goes from concave upward to concave downward (or vice versa). Explain the concavity test for a function over an open interval. When the sign of the first derivative (ie of the. Point Of Inflection Third Derivative.
From lakschool.com
Inflection point Math examples Point Of Inflection Third Derivative There are two types of inflection points: When the second derivative is negative, the function is concave downward. What is a point of inflection? Use concavity and inflection points to explain how the sign of the second derivative affects the shape of a function’s graph. When the sign of the first derivative (ie of the gradient) is the same on. Point Of Inflection Third Derivative.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Point Of Inflection Third Derivative Use concavity and inflection points to explain how the sign of the second derivative affects the shape of a function’s graph. When the sign of the first derivative (ie of the gradient) is the same on both. Given a curve y=f(x), a point of inflection is a point at which the second derivative equals to zero, f''(x)=0, and across which. Point Of Inflection Third Derivative.
From www.nagwa.com
Question Video Finding the Inflection Points of a Function from the Point Of Inflection Third Derivative Explain the concavity test for a function over an open interval. Calculate the value of the function at the x value for the point of. And the inflection point is where it goes from concave upward to concave downward (or vice versa). When the sign of the first derivative (ie of the gradient) is the same on both. Given a. Point Of Inflection Third Derivative.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Point Of Inflection Third Derivative Explain the concavity test for a function over an open interval. What is a point of inflection? Decide whether you have a minimum/maximum or a point of inflection. There are two types of inflection points: Calculate the value of the function at the x value for the point of. When the sign of the first derivative (ie of the gradient). Point Of Inflection Third Derivative.
From www.easysevens.com
Derivatives Local Maximum, Minimum and Point of Inflection Point Of Inflection Third Derivative Use concavity and inflection points to explain how the sign of the second derivative affects the shape of a function’s graph. And the inflection point is where it goes from concave upward to concave downward (or vice versa). Calculate the value of the function at the x value for the point of. When the sign of the first derivative (ie. Point Of Inflection Third Derivative.