Dimensional Numbers . 75 rows dimensionless numbers (or characteristic numbers) have an important role in analyzing the behavior of fluids and their flow. The dimensionless numbers since many of them have formulated in a certain field tend to be duplicated. Dimensionless numbers and scaling laws provide elegant insights into the characteristic properties of physical systems. In fact, in the study of the physical situations often people refers to local \ (re\) number and the global \ (re\) number. Some important dimensionless numbers used in fluid mechanics and their importance is explained below. Where, µ = viscosity of fluid (kg/m.s) d = diameter of pipe (m) Dimensional analysis provides a powerful and unambiguous way of querying (and ultimately answering) someone who blithely. It describes the predominance of inertia forces to the viscous forces occurring in the flow systems. Explore the world of dimensionless numbers in process engineering, including reynolds, prandtl, fourier, euler, and more. Reynolds number is the ratio of inertia force to the viscous force.
from dmr-physicsnotes.blogspot.com
The dimensionless numbers since many of them have formulated in a certain field tend to be duplicated. Dimensionless numbers and scaling laws provide elegant insights into the characteristic properties of physical systems. Explore the world of dimensionless numbers in process engineering, including reynolds, prandtl, fourier, euler, and more. It describes the predominance of inertia forces to the viscous forces occurring in the flow systems. Dimensional analysis provides a powerful and unambiguous way of querying (and ultimately answering) someone who blithely. In fact, in the study of the physical situations often people refers to local \ (re\) number and the global \ (re\) number. Reynolds number is the ratio of inertia force to the viscous force. Some important dimensionless numbers used in fluid mechanics and their importance is explained below. 75 rows dimensionless numbers (or characteristic numbers) have an important role in analyzing the behavior of fluids and their flow. Where, µ = viscosity of fluid (kg/m.s) d = diameter of pipe (m)
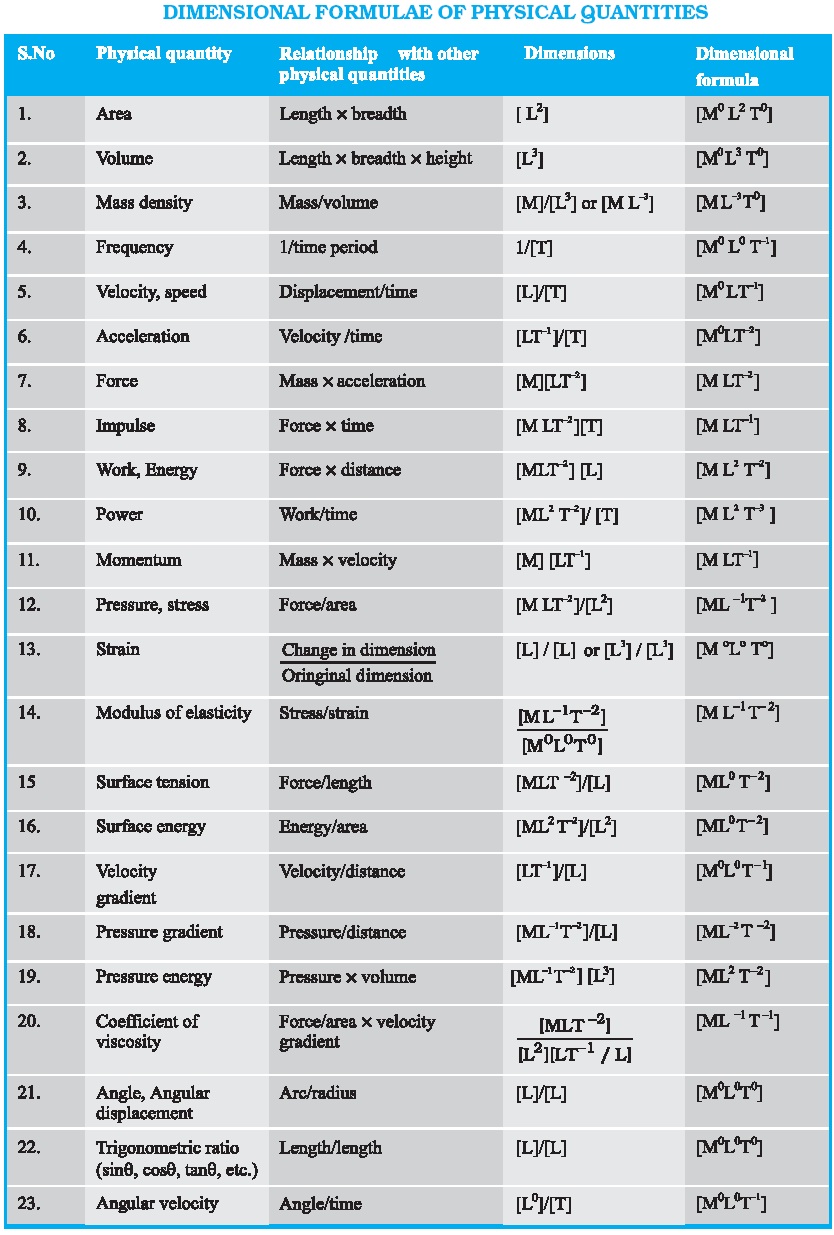
DMR'S PHYSICS NOTES Dimensional Formulae
Dimensional Numbers Where, µ = viscosity of fluid (kg/m.s) d = diameter of pipe (m) It describes the predominance of inertia forces to the viscous forces occurring in the flow systems. Explore the world of dimensionless numbers in process engineering, including reynolds, prandtl, fourier, euler, and more. Some important dimensionless numbers used in fluid mechanics and their importance is explained below. The dimensionless numbers since many of them have formulated in a certain field tend to be duplicated. Dimensional analysis provides a powerful and unambiguous way of querying (and ultimately answering) someone who blithely. In fact, in the study of the physical situations often people refers to local \ (re\) number and the global \ (re\) number. 75 rows dimensionless numbers (or characteristic numbers) have an important role in analyzing the behavior of fluids and their flow. Where, µ = viscosity of fluid (kg/m.s) d = diameter of pipe (m) Reynolds number is the ratio of inertia force to the viscous force. Dimensionless numbers and scaling laws provide elegant insights into the characteristic properties of physical systems.
From www.dreamstime.com
Threedimensional Numbers. 3d Rendering. Set Numbers. Isometric Dimensional Numbers In fact, in the study of the physical situations often people refers to local \ (re\) number and the global \ (re\) number. It describes the predominance of inertia forces to the viscous forces occurring in the flow systems. Explore the world of dimensionless numbers in process engineering, including reynolds, prandtl, fourier, euler, and more. Reynolds number is the ratio. Dimensional Numbers.
From www.askiitians.com
IIT JEE Dimensional Formulae and Dimensional Equations JEE Physics Dimensional Numbers In fact, in the study of the physical situations often people refers to local \ (re\) number and the global \ (re\) number. Some important dimensionless numbers used in fluid mechanics and their importance is explained below. Where, µ = viscosity of fluid (kg/m.s) d = diameter of pipe (m) Reynolds number is the ratio of inertia force to the. Dimensional Numbers.
From www.alamy.com
Three dimensional numbers hires stock photography and images Alamy Dimensional Numbers It describes the predominance of inertia forces to the viscous forces occurring in the flow systems. 75 rows dimensionless numbers (or characteristic numbers) have an important role in analyzing the behavior of fluids and their flow. Dimensionless numbers and scaling laws provide elegant insights into the characteristic properties of physical systems. Where, µ = viscosity of fluid (kg/m.s) d =. Dimensional Numbers.
From www.alamy.com
Composite image of three dimensional numbers with red arrow Stock Photo Dimensional Numbers Reynolds number is the ratio of inertia force to the viscous force. Explore the world of dimensionless numbers in process engineering, including reynolds, prandtl, fourier, euler, and more. In fact, in the study of the physical situations often people refers to local \ (re\) number and the global \ (re\) number. Dimensionless numbers and scaling laws provide elegant insights into. Dimensional Numbers.
From www.dreamstime.com
Three dimensional numbers stock vector. Illustration of creative Dimensional Numbers In fact, in the study of the physical situations often people refers to local \ (re\) number and the global \ (re\) number. Reynolds number is the ratio of inertia force to the viscous force. The dimensionless numbers since many of them have formulated in a certain field tend to be duplicated. Some important dimensionless numbers used in fluid mechanics. Dimensional Numbers.
From www.shutterstock.com
Collection Of 10 Colorful ThreeDimensional Numbers. Stock Vector Dimensional Numbers Reynolds number is the ratio of inertia force to the viscous force. Some important dimensionless numbers used in fluid mechanics and their importance is explained below. Dimensional analysis provides a powerful and unambiguous way of querying (and ultimately answering) someone who blithely. Where, µ = viscosity of fluid (kg/m.s) d = diameter of pipe (m) Dimensionless numbers and scaling laws. Dimensional Numbers.
From www.vectorstock.com
3D numbers and symbols Threedimensional Vector Image Dimensional Numbers The dimensionless numbers since many of them have formulated in a certain field tend to be duplicated. In fact, in the study of the physical situations often people refers to local \ (re\) number and the global \ (re\) number. 75 rows dimensionless numbers (or characteristic numbers) have an important role in analyzing the behavior of fluids and their flow.. Dimensional Numbers.
From www.dreamstime.com
Three dimensional numbers stock illustration. Illustration of chrome Dimensional Numbers 75 rows dimensionless numbers (or characteristic numbers) have an important role in analyzing the behavior of fluids and their flow. The dimensionless numbers since many of them have formulated in a certain field tend to be duplicated. Some important dimensionless numbers used in fluid mechanics and their importance is explained below. In fact, in the study of the physical situations. Dimensional Numbers.
From pngtree.com
Realistic Three Dimensional Number Set PNG, Vector, PSD, and Clipart Dimensional Numbers Dimensionless numbers and scaling laws provide elegant insights into the characteristic properties of physical systems. Some important dimensionless numbers used in fluid mechanics and their importance is explained below. In fact, in the study of the physical situations often people refers to local \ (re\) number and the global \ (re\) number. Reynolds number is the ratio of inertia force. Dimensional Numbers.
From www.colourbox.com
Collection of 10 threedimensional numbers on white background Stock Dimensional Numbers The dimensionless numbers since many of them have formulated in a certain field tend to be duplicated. Explore the world of dimensionless numbers in process engineering, including reynolds, prandtl, fourier, euler, and more. It describes the predominance of inertia forces to the viscous forces occurring in the flow systems. Dimensionless numbers and scaling laws provide elegant insights into the characteristic. Dimensional Numbers.
From www.alamy.com
Three Dimensional Numbers High Resolution Stock Photography and Images Dimensional Numbers Reynolds number is the ratio of inertia force to the viscous force. The dimensionless numbers since many of them have formulated in a certain field tend to be duplicated. It describes the predominance of inertia forces to the viscous forces occurring in the flow systems. 75 rows dimensionless numbers (or characteristic numbers) have an important role in analyzing the behavior. Dimensional Numbers.
From www.vectorstock.com
Set threedimensional numbers with winter decor Vector Image Dimensional Numbers Explore the world of dimensionless numbers in process engineering, including reynolds, prandtl, fourier, euler, and more. In fact, in the study of the physical situations often people refers to local \ (re\) number and the global \ (re\) number. Dimensional analysis provides a powerful and unambiguous way of querying (and ultimately answering) someone who blithely. 75 rows dimensionless numbers (or. Dimensional Numbers.
From dmr-physicsnotes.blogspot.com
DMR'S PHYSICS NOTES Dimensional Formulae Dimensional Numbers It describes the predominance of inertia forces to the viscous forces occurring in the flow systems. In fact, in the study of the physical situations often people refers to local \ (re\) number and the global \ (re\) number. Reynolds number is the ratio of inertia force to the viscous force. Explore the world of dimensionless numbers in process engineering,. Dimensional Numbers.
From www.scribd.com
Dimensional Numbers in Fluid Mechanics PDF Fluid Dynamics Viscosity Dimensional Numbers Explore the world of dimensionless numbers in process engineering, including reynolds, prandtl, fourier, euler, and more. Dimensionless numbers and scaling laws provide elegant insights into the characteristic properties of physical systems. In fact, in the study of the physical situations often people refers to local \ (re\) number and the global \ (re\) number. The dimensionless numbers since many of. Dimensional Numbers.
From www.chegg.com
Consider an Ndimensional space of real numbers An Dimensional Numbers The dimensionless numbers since many of them have formulated in a certain field tend to be duplicated. Explore the world of dimensionless numbers in process engineering, including reynolds, prandtl, fourier, euler, and more. Reynolds number is the ratio of inertia force to the viscous force. Where, µ = viscosity of fluid (kg/m.s) d = diameter of pipe (m) It describes. Dimensional Numbers.
From www.vectorstock.com
Rotated striped dimensional numbers geometric Vector Image Dimensional Numbers In fact, in the study of the physical situations often people refers to local \ (re\) number and the global \ (re\) number. Explore the world of dimensionless numbers in process engineering, including reynolds, prandtl, fourier, euler, and more. 75 rows dimensionless numbers (or characteristic numbers) have an important role in analyzing the behavior of fluids and their flow. Where,. Dimensional Numbers.
From www.dreamstime.com
Three dimensional numbers stock illustration. Illustration of three Dimensional Numbers In fact, in the study of the physical situations often people refers to local \ (re\) number and the global \ (re\) number. Dimensional analysis provides a powerful and unambiguous way of querying (and ultimately answering) someone who blithely. The dimensionless numbers since many of them have formulated in a certain field tend to be duplicated. It describes the predominance. Dimensional Numbers.
From artprojectsforkids.org
Easy How to Draw 3D Numbers Tutorial and 3D Numbers Coloring Page Dimensional Numbers Where, µ = viscosity of fluid (kg/m.s) d = diameter of pipe (m) In fact, in the study of the physical situations often people refers to local \ (re\) number and the global \ (re\) number. Explore the world of dimensionless numbers in process engineering, including reynolds, prandtl, fourier, euler, and more. Some important dimensionless numbers used in fluid mechanics. Dimensional Numbers.
From www.dreamstime.com
Realistic Three Dimensional Set of Numbers. Isometric Numbers Vector Dimensional Numbers Where, µ = viscosity of fluid (kg/m.s) d = diameter of pipe (m) It describes the predominance of inertia forces to the viscous forces occurring in the flow systems. Dimensional analysis provides a powerful and unambiguous way of querying (and ultimately answering) someone who blithely. Dimensionless numbers and scaling laws provide elegant insights into the characteristic properties of physical systems.. Dimensional Numbers.
From www.dreamstime.com
Three dimensional numbers stock illustration. Illustration of design Dimensional Numbers The dimensionless numbers since many of them have formulated in a certain field tend to be duplicated. 75 rows dimensionless numbers (or characteristic numbers) have an important role in analyzing the behavior of fluids and their flow. In fact, in the study of the physical situations often people refers to local \ (re\) number and the global \ (re\) number.. Dimensional Numbers.
From www.researchgate.net
1 Important dimensionless numbers in multiphase flows Download Table Dimensional Numbers Dimensionless numbers and scaling laws provide elegant insights into the characteristic properties of physical systems. 75 rows dimensionless numbers (or characteristic numbers) have an important role in analyzing the behavior of fluids and their flow. Where, µ = viscosity of fluid (kg/m.s) d = diameter of pipe (m) Reynolds number is the ratio of inertia force to the viscous force.. Dimensional Numbers.
From www.cuemath.com
Learn about Geometric shapes and their properties Cuemath Dimensional Numbers Explore the world of dimensionless numbers in process engineering, including reynolds, prandtl, fourier, euler, and more. It describes the predominance of inertia forces to the viscous forces occurring in the flow systems. The dimensionless numbers since many of them have formulated in a certain field tend to be duplicated. Dimensional analysis provides a powerful and unambiguous way of querying (and. Dimensional Numbers.
From www.dreamstime.com
Threedimensional Numbers. 3d Rendering. Set Numbers. Isometric Dimensional Numbers Explore the world of dimensionless numbers in process engineering, including reynolds, prandtl, fourier, euler, and more. It describes the predominance of inertia forces to the viscous forces occurring in the flow systems. Dimensionless numbers and scaling laws provide elegant insights into the characteristic properties of physical systems. The dimensionless numbers since many of them have formulated in a certain field. Dimensional Numbers.
From www.dreamstime.com
Dimensional Numbers with Rotation Effect, 3d Digits. Stock Vector Dimensional Numbers The dimensionless numbers since many of them have formulated in a certain field tend to be duplicated. Explore the world of dimensionless numbers in process engineering, including reynolds, prandtl, fourier, euler, and more. It describes the predominance of inertia forces to the viscous forces occurring in the flow systems. In fact, in the study of the physical situations often people. Dimensional Numbers.
From www.dreamstime.com
Composite Image of Digital Image of Three Dimensional Numbers Stock Dimensional Numbers Where, µ = viscosity of fluid (kg/m.s) d = diameter of pipe (m) 75 rows dimensionless numbers (or characteristic numbers) have an important role in analyzing the behavior of fluids and their flow. Explore the world of dimensionless numbers in process engineering, including reynolds, prandtl, fourier, euler, and more. Dimensionless numbers and scaling laws provide elegant insights into the characteristic. Dimensional Numbers.
From www.alamy.com
Abstract background from set of threedimensional numbers Stock Photo Dimensional Numbers Explore the world of dimensionless numbers in process engineering, including reynolds, prandtl, fourier, euler, and more. Where, µ = viscosity of fluid (kg/m.s) d = diameter of pipe (m) 75 rows dimensionless numbers (or characteristic numbers) have an important role in analyzing the behavior of fluids and their flow. Some important dimensionless numbers used in fluid mechanics and their importance. Dimensional Numbers.
From stock.adobe.com
Rotated smooth dimensional numbers, vector geometric numeration. Stock Dimensional Numbers Explore the world of dimensionless numbers in process engineering, including reynolds, prandtl, fourier, euler, and more. Where, µ = viscosity of fluid (kg/m.s) d = diameter of pipe (m) In fact, in the study of the physical situations often people refers to local \ (re\) number and the global \ (re\) number. Some important dimensionless numbers used in fluid mechanics. Dimensional Numbers.
From www.alamy.com
Concrete digits three dimensional numbers on white background 3d Dimensional Numbers The dimensionless numbers since many of them have formulated in a certain field tend to be duplicated. Dimensional analysis provides a powerful and unambiguous way of querying (and ultimately answering) someone who blithely. Where, µ = viscosity of fluid (kg/m.s) d = diameter of pipe (m) It describes the predominance of inertia forces to the viscous forces occurring in the. Dimensional Numbers.
From www.dreamstime.com
Threedimensional numbers. stock vector. Illustration of banner 46640769 Dimensional Numbers It describes the predominance of inertia forces to the viscous forces occurring in the flow systems. Some important dimensionless numbers used in fluid mechanics and their importance is explained below. The dimensionless numbers since many of them have formulated in a certain field tend to be duplicated. Reynolds number is the ratio of inertia force to the viscous force. 75. Dimensional Numbers.
From www.alamy.com
Dimensional Life of Numbers Stock Photo Alamy Dimensional Numbers Where, µ = viscosity of fluid (kg/m.s) d = diameter of pipe (m) It describes the predominance of inertia forces to the viscous forces occurring in the flow systems. Dimensionless numbers and scaling laws provide elegant insights into the characteristic properties of physical systems. Dimensional analysis provides a powerful and unambiguous way of querying (and ultimately answering) someone who blithely.. Dimensional Numbers.
From www.freepik.com
Premium Vector Threedimensional number set 09 with percent off Dimensional Numbers The dimensionless numbers since many of them have formulated in a certain field tend to be duplicated. Reynolds number is the ratio of inertia force to the viscous force. Where, µ = viscosity of fluid (kg/m.s) d = diameter of pipe (m) In fact, in the study of the physical situations often people refers to local \ (re\) number and. Dimensional Numbers.
From www.dreamstime.com
Realistic Three Dimensional Number Typeset Stock Illustration Dimensional Numbers Dimensional analysis provides a powerful and unambiguous way of querying (and ultimately answering) someone who blithely. Dimensionless numbers and scaling laws provide elegant insights into the characteristic properties of physical systems. Explore the world of dimensionless numbers in process engineering, including reynolds, prandtl, fourier, euler, and more. In fact, in the study of the physical situations often people refers to. Dimensional Numbers.
From www.dreamstime.com
3D Numbers Set stock vector. Illustration of graphic 20411555 Dimensional Numbers Explore the world of dimensionless numbers in process engineering, including reynolds, prandtl, fourier, euler, and more. Reynolds number is the ratio of inertia force to the viscous force. It describes the predominance of inertia forces to the viscous forces occurring in the flow systems. Where, µ = viscosity of fluid (kg/m.s) d = diameter of pipe (m) In fact, in. Dimensional Numbers.
From depositphotos.com
Dimensional numbers with rotation effect, perspective unusual nu Stock Dimensional Numbers 75 rows dimensionless numbers (or characteristic numbers) have an important role in analyzing the behavior of fluids and their flow. Dimensionless numbers and scaling laws provide elegant insights into the characteristic properties of physical systems. It describes the predominance of inertia forces to the viscous forces occurring in the flow systems. Where, µ = viscosity of fluid (kg/m.s) d =. Dimensional Numbers.
From www.alamy.com
Three dimensional numbers hires stock photography and images Alamy Dimensional Numbers In fact, in the study of the physical situations often people refers to local \ (re\) number and the global \ (re\) number. It describes the predominance of inertia forces to the viscous forces occurring in the flow systems. Some important dimensionless numbers used in fluid mechanics and their importance is explained below. Dimensional analysis provides a powerful and unambiguous. Dimensional Numbers.