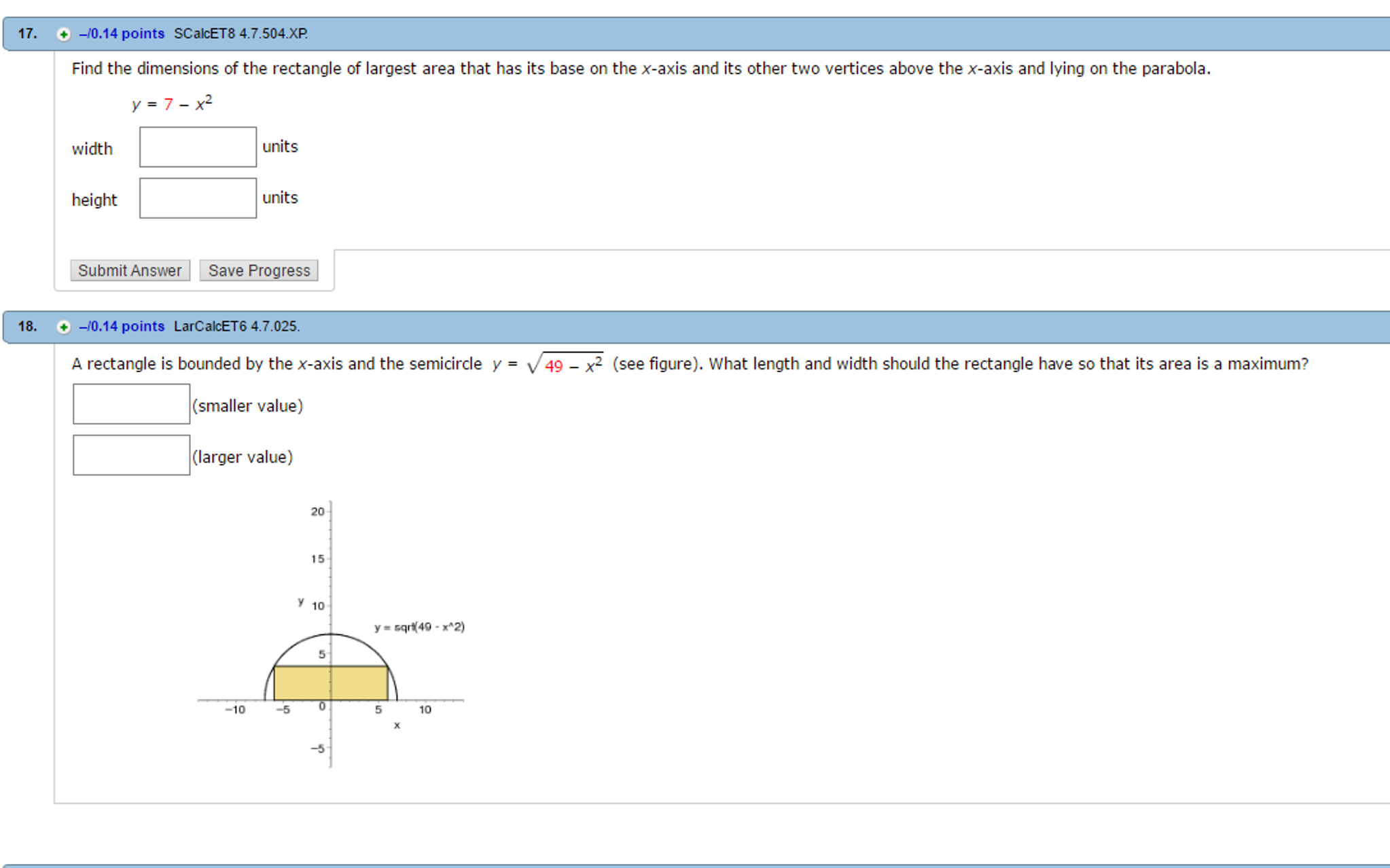
What Are The Dimensions Of The Largest Rectangular . Find the largest possible rectangular area you can enclose, assuming you have 128 meters of fencing. The value of y will be given by y = √r2 −(1 √2 r)2 = √1 2 r2 = 1 √2 r. You should take the dimensions of the rectangle as $2x,2y$ and $2z$ instead of $x,y$ and $z$. The perimeter (p) of a rectangle is the sum of all the individual sides of a rectangle, i.e., p = 2x(a+b). X = 1 √2 r. What is the (geometric) significance of. Find the dimensions of the largest rectangle that can be inscribed in a semicircle of radius r. Our dimensions of a rectangle. The result you need is that for a rectangle with a given perimeter the square has the largest area. So with a perimeter of 28 feet,. Thus the shape will be a square of dimensions 1 √2 r by 1 √2 r, giving a maximum area of 1 2. Use the method of lagrange multipliers to find the dimensions of the rectangle of greatest area that can be inscribed in the.
from www.chegg.com
X = 1 √2 r. Our dimensions of a rectangle. Thus the shape will be a square of dimensions 1 √2 r by 1 √2 r, giving a maximum area of 1 2. The value of y will be given by y = √r2 −(1 √2 r)2 = √1 2 r2 = 1 √2 r. Use the method of lagrange multipliers to find the dimensions of the rectangle of greatest area that can be inscribed in the. The result you need is that for a rectangle with a given perimeter the square has the largest area. So with a perimeter of 28 feet,. You should take the dimensions of the rectangle as $2x,2y$ and $2z$ instead of $x,y$ and $z$. Find the largest possible rectangular area you can enclose, assuming you have 128 meters of fencing. What is the (geometric) significance of.
Solved Find the dimensions of the rectangle of largest area
What Are The Dimensions Of The Largest Rectangular Find the largest possible rectangular area you can enclose, assuming you have 128 meters of fencing. You should take the dimensions of the rectangle as $2x,2y$ and $2z$ instead of $x,y$ and $z$. Find the dimensions of the largest rectangle that can be inscribed in a semicircle of radius r. Thus the shape will be a square of dimensions 1 √2 r by 1 √2 r, giving a maximum area of 1 2. X = 1 √2 r. Use the method of lagrange multipliers to find the dimensions of the rectangle of greatest area that can be inscribed in the. Our dimensions of a rectangle. Find the largest possible rectangular area you can enclose, assuming you have 128 meters of fencing. The value of y will be given by y = √r2 −(1 √2 r)2 = √1 2 r2 = 1 √2 r. The perimeter (p) of a rectangle is the sum of all the individual sides of a rectangle, i.e., p = 2x(a+b). What is the (geometric) significance of. So with a perimeter of 28 feet,. The result you need is that for a rectangle with a given perimeter the square has the largest area.
From www.coursehero.com
[Solved] What are the dimensions of the largest rectangular piece that What Are The Dimensions Of The Largest Rectangular X = 1 √2 r. Find the dimensions of the largest rectangle that can be inscribed in a semicircle of radius r. Find the largest possible rectangular area you can enclose, assuming you have 128 meters of fencing. You should take the dimensions of the rectangle as $2x,2y$ and $2z$ instead of $x,y$ and $z$. The perimeter (p) of a. What Are The Dimensions Of The Largest Rectangular.
From www.chegg.com
Solved Find the dimensions of the largest rectangle that can What Are The Dimensions Of The Largest Rectangular The result you need is that for a rectangle with a given perimeter the square has the largest area. You should take the dimensions of the rectangle as $2x,2y$ and $2z$ instead of $x,y$ and $z$. Find the dimensions of the largest rectangle that can be inscribed in a semicircle of radius r. X = 1 √2 r. The value. What Are The Dimensions Of The Largest Rectangular.
From www.chegg.com
Solved Find the dimensions of the rectangle of largest area What Are The Dimensions Of The Largest Rectangular Find the dimensions of the largest rectangle that can be inscribed in a semicircle of radius r. X = 1 √2 r. Use the method of lagrange multipliers to find the dimensions of the rectangle of greatest area that can be inscribed in the. Find the largest possible rectangular area you can enclose, assuming you have 128 meters of fencing.. What Are The Dimensions Of The Largest Rectangular.
From www.chegg.com
Solved Find the dimensions and the area of the largest What Are The Dimensions Of The Largest Rectangular You should take the dimensions of the rectangle as $2x,2y$ and $2z$ instead of $x,y$ and $z$. Find the dimensions of the largest rectangle that can be inscribed in a semicircle of radius r. Thus the shape will be a square of dimensions 1 √2 r by 1 √2 r, giving a maximum area of 1 2. So with a. What Are The Dimensions Of The Largest Rectangular.
From www.chegg.com
Solved Question 2 (a) What are the dimensions of the largest What Are The Dimensions Of The Largest Rectangular So with a perimeter of 28 feet,. You should take the dimensions of the rectangle as $2x,2y$ and $2z$ instead of $x,y$ and $z$. Use the method of lagrange multipliers to find the dimensions of the rectangle of greatest area that can be inscribed in the. The perimeter (p) of a rectangle is the sum of all the individual sides. What Are The Dimensions Of The Largest Rectangular.
From www.coursehero.com
[Solved] . What are the dimensions of the largest rectangular piece What Are The Dimensions Of The Largest Rectangular Find the dimensions of the largest rectangle that can be inscribed in a semicircle of radius r. You should take the dimensions of the rectangle as $2x,2y$ and $2z$ instead of $x,y$ and $z$. The result you need is that for a rectangle with a given perimeter the square has the largest area. Find the largest possible rectangular area you. What Are The Dimensions Of The Largest Rectangular.
From www.chegg.com
Solved Find the dimensions of the rectangle of largest area What Are The Dimensions Of The Largest Rectangular The result you need is that for a rectangle with a given perimeter the square has the largest area. So with a perimeter of 28 feet,. Thus the shape will be a square of dimensions 1 √2 r by 1 √2 r, giving a maximum area of 1 2. Find the largest possible rectangular area you can enclose, assuming you. What Are The Dimensions Of The Largest Rectangular.
From www.coursehero.com
[Solved] What are the dimensions of the largest rectangular piece that What Are The Dimensions Of The Largest Rectangular You should take the dimensions of the rectangle as $2x,2y$ and $2z$ instead of $x,y$ and $z$. So with a perimeter of 28 feet,. X = 1 √2 r. What is the (geometric) significance of. Thus the shape will be a square of dimensions 1 √2 r by 1 √2 r, giving a maximum area of 1 2. The value. What Are The Dimensions Of The Largest Rectangular.
From www.youtube.com
Dimensions of a Rectangle Visualizing Algebra YouTube What Are The Dimensions Of The Largest Rectangular The value of y will be given by y = √r2 −(1 √2 r)2 = √1 2 r2 = 1 √2 r. Find the dimensions of the largest rectangle that can be inscribed in a semicircle of radius r. The result you need is that for a rectangle with a given perimeter the square has the largest area. So with. What Are The Dimensions Of The Largest Rectangular.
From quizlet.com
***Area*** Find the dimensions of the largest rectangle that Quizlet What Are The Dimensions Of The Largest Rectangular Use the method of lagrange multipliers to find the dimensions of the rectangle of greatest area that can be inscribed in the. You should take the dimensions of the rectangle as $2x,2y$ and $2z$ instead of $x,y$ and $z$. Thus the shape will be a square of dimensions 1 √2 r by 1 √2 r, giving a maximum area of. What Are The Dimensions Of The Largest Rectangular.
From www.coursehero.com
[Solved] 13. Find the dimensions of the rectangle of largest area that What Are The Dimensions Of The Largest Rectangular So with a perimeter of 28 feet,. The value of y will be given by y = √r2 −(1 √2 r)2 = √1 2 r2 = 1 √2 r. You should take the dimensions of the rectangle as $2x,2y$ and $2z$ instead of $x,y$ and $z$. Find the dimensions of the largest rectangle that can be inscribed in a semicircle. What Are The Dimensions Of The Largest Rectangular.
From www.chegg.com
Solved Determine the dimensions of the rectangle of largest What Are The Dimensions Of The Largest Rectangular The value of y will be given by y = √r2 −(1 √2 r)2 = √1 2 r2 = 1 √2 r. So with a perimeter of 28 feet,. The result you need is that for a rectangle with a given perimeter the square has the largest area. You should take the dimensions of the rectangle as $2x,2y$ and $2z$. What Are The Dimensions Of The Largest Rectangular.
From www.chegg.com
Solved Find the dimensions of the rectangle of largest area What Are The Dimensions Of The Largest Rectangular The perimeter (p) of a rectangle is the sum of all the individual sides of a rectangle, i.e., p = 2x(a+b). Thus the shape will be a square of dimensions 1 √2 r by 1 √2 r, giving a maximum area of 1 2. The value of y will be given by y = √r2 −(1 √2 r)2 = √1. What Are The Dimensions Of The Largest Rectangular.
From oneclass.com
OneClass 1. Find the dimensions of the largest rectangle that can be What Are The Dimensions Of The Largest Rectangular Use the method of lagrange multipliers to find the dimensions of the rectangle of greatest area that can be inscribed in the. X = 1 √2 r. Find the dimensions of the largest rectangle that can be inscribed in a semicircle of radius r. You should take the dimensions of the rectangle as $2x,2y$ and $2z$ instead of $x,y$ and. What Are The Dimensions Of The Largest Rectangular.
From www.youtube.com
Find the dimensions of the rectangle given that the area is 68 sq feet What Are The Dimensions Of The Largest Rectangular X = 1 √2 r. Thus the shape will be a square of dimensions 1 √2 r by 1 √2 r, giving a maximum area of 1 2. Find the largest possible rectangular area you can enclose, assuming you have 128 meters of fencing. Find the dimensions of the largest rectangle that can be inscribed in a semicircle of radius. What Are The Dimensions Of The Largest Rectangular.
From www.coursehero.com
[Solved] Find the dimensions of the rectangle of largest area that has What Are The Dimensions Of The Largest Rectangular Thus the shape will be a square of dimensions 1 √2 r by 1 √2 r, giving a maximum area of 1 2. Find the dimensions of the largest rectangle that can be inscribed in a semicircle of radius r. Find the largest possible rectangular area you can enclose, assuming you have 128 meters of fencing. The result you need. What Are The Dimensions Of The Largest Rectangular.
From www.chegg.com
Solved Find the dimensions and the area of the largest What Are The Dimensions Of The Largest Rectangular You should take the dimensions of the rectangle as $2x,2y$ and $2z$ instead of $x,y$ and $z$. The perimeter (p) of a rectangle is the sum of all the individual sides of a rectangle, i.e., p = 2x(a+b). Find the dimensions of the largest rectangle that can be inscribed in a semicircle of radius r. Find the largest possible rectangular. What Are The Dimensions Of The Largest Rectangular.
From www.toppr.com
Find the largest size of a rectangle that can be inscribed in a What Are The Dimensions Of The Largest Rectangular Find the dimensions of the largest rectangle that can be inscribed in a semicircle of radius r. So with a perimeter of 28 feet,. You should take the dimensions of the rectangle as $2x,2y$ and $2z$ instead of $x,y$ and $z$. Find the largest possible rectangular area you can enclose, assuming you have 128 meters of fencing. The value of. What Are The Dimensions Of The Largest Rectangular.
From www.chegg.com
Solved Determine the dimensions of the rectangle of largest What Are The Dimensions Of The Largest Rectangular What is the (geometric) significance of. The perimeter (p) of a rectangle is the sum of all the individual sides of a rectangle, i.e., p = 2x(a+b). X = 1 √2 r. Thus the shape will be a square of dimensions 1 √2 r by 1 √2 r, giving a maximum area of 1 2. You should take the dimensions. What Are The Dimensions Of The Largest Rectangular.
From www.numerade.com
SOLVED find the dimensions of the largest rectangle which can be What Are The Dimensions Of The Largest Rectangular Use the method of lagrange multipliers to find the dimensions of the rectangle of greatest area that can be inscribed in the. Our dimensions of a rectangle. You should take the dimensions of the rectangle as $2x,2y$ and $2z$ instead of $x,y$ and $z$. The perimeter (p) of a rectangle is the sum of all the individual sides of a. What Are The Dimensions Of The Largest Rectangular.
From www.mathskey.com
Find the area of the largest rectangle that fits inside a circle of What Are The Dimensions Of The Largest Rectangular The perimeter (p) of a rectangle is the sum of all the individual sides of a rectangle, i.e., p = 2x(a+b). So with a perimeter of 28 feet,. You should take the dimensions of the rectangle as $2x,2y$ and $2z$ instead of $x,y$ and $z$. Find the largest possible rectangular area you can enclose, assuming you have 128 meters of. What Are The Dimensions Of The Largest Rectangular.
From www.chegg.com
Solved Find the dimensions and the area of the largest What Are The Dimensions Of The Largest Rectangular You should take the dimensions of the rectangle as $2x,2y$ and $2z$ instead of $x,y$ and $z$. Use the method of lagrange multipliers to find the dimensions of the rectangle of greatest area that can be inscribed in the. Our dimensions of a rectangle. The perimeter (p) of a rectangle is the sum of all the individual sides of a. What Are The Dimensions Of The Largest Rectangular.
From www.chegg.com
Solved Find the dimensions of the largest rectangle that can What Are The Dimensions Of The Largest Rectangular Thus the shape will be a square of dimensions 1 √2 r by 1 √2 r, giving a maximum area of 1 2. Find the dimensions of the largest rectangle that can be inscribed in a semicircle of radius r. The perimeter (p) of a rectangle is the sum of all the individual sides of a rectangle, i.e., p =. What Are The Dimensions Of The Largest Rectangular.
From www.geeksforgeeks.org
Area of the largest Rectangle without a given point What Are The Dimensions Of The Largest Rectangular The result you need is that for a rectangle with a given perimeter the square has the largest area. Thus the shape will be a square of dimensions 1 √2 r by 1 √2 r, giving a maximum area of 1 2. What is the (geometric) significance of. You should take the dimensions of the rectangle as $2x,2y$ and $2z$. What Are The Dimensions Of The Largest Rectangular.
From www.numerade.com
SOLVEDFind the dimensions of the rectangle of largest area that can be What Are The Dimensions Of The Largest Rectangular The perimeter (p) of a rectangle is the sum of all the individual sides of a rectangle, i.e., p = 2x(a+b). The value of y will be given by y = √r2 −(1 √2 r)2 = √1 2 r2 = 1 √2 r. Use the method of lagrange multipliers to find the dimensions of the rectangle of greatest area that. What Are The Dimensions Of The Largest Rectangular.
From kunduz.com
[ANSWERED] What are the dimensions of the rectangle with largest area What Are The Dimensions Of The Largest Rectangular Use the method of lagrange multipliers to find the dimensions of the rectangle of greatest area that can be inscribed in the. Find the dimensions of the largest rectangle that can be inscribed in a semicircle of radius r. You should take the dimensions of the rectangle as $2x,2y$ and $2z$ instead of $x,y$ and $z$. The value of y. What Are The Dimensions Of The Largest Rectangular.
From www.numerade.com
SOLVED What are the dimensions of the largest rectangular piece that What Are The Dimensions Of The Largest Rectangular The value of y will be given by y = √r2 −(1 √2 r)2 = √1 2 r2 = 1 √2 r. You should take the dimensions of the rectangle as $2x,2y$ and $2z$ instead of $x,y$ and $z$. Our dimensions of a rectangle. Thus the shape will be a square of dimensions 1 √2 r by 1 √2 r,. What Are The Dimensions Of The Largest Rectangular.
From www.youtube.com
Find the dimensions of a rectangle. YouTube What Are The Dimensions Of The Largest Rectangular The result you need is that for a rectangle with a given perimeter the square has the largest area. Find the largest possible rectangular area you can enclose, assuming you have 128 meters of fencing. The value of y will be given by y = √r2 −(1 √2 r)2 = √1 2 r2 = 1 √2 r. Use the method. What Are The Dimensions Of The Largest Rectangular.
From www.chegg.com
Solved Find the dimensions of the largest rectangle that can What Are The Dimensions Of The Largest Rectangular X = 1 √2 r. What is the (geometric) significance of. You should take the dimensions of the rectangle as $2x,2y$ and $2z$ instead of $x,y$ and $z$. The value of y will be given by y = √r2 −(1 √2 r)2 = √1 2 r2 = 1 √2 r. Our dimensions of a rectangle. The perimeter (p) of a. What Are The Dimensions Of The Largest Rectangular.
From www.numerade.com
SOLVED "What are the dimensions of the largest rectangular piece that What Are The Dimensions Of The Largest Rectangular Find the dimensions of the largest rectangle that can be inscribed in a semicircle of radius r. Find the largest possible rectangular area you can enclose, assuming you have 128 meters of fencing. The result you need is that for a rectangle with a given perimeter the square has the largest area. Our dimensions of a rectangle. The value of. What Are The Dimensions Of The Largest Rectangular.
From www.numerade.com
SOLVED 4 What are the dimensions of the largest rectangular field that What Are The Dimensions Of The Largest Rectangular Find the dimensions of the largest rectangle that can be inscribed in a semicircle of radius r. The value of y will be given by y = √r2 −(1 √2 r)2 = √1 2 r2 = 1 √2 r. Our dimensions of a rectangle. The perimeter (p) of a rectangle is the sum of all the individual sides of a. What Are The Dimensions Of The Largest Rectangular.
From www.chegg.com
Solved What are the dimensions of the largest rectangular What Are The Dimensions Of The Largest Rectangular Our dimensions of a rectangle. What is the (geometric) significance of. You should take the dimensions of the rectangle as $2x,2y$ and $2z$ instead of $x,y$ and $z$. The value of y will be given by y = √r2 −(1 √2 r)2 = √1 2 r2 = 1 √2 r. So with a perimeter of 28 feet,. X = 1. What Are The Dimensions Of The Largest Rectangular.
From www.coursehero.com
[Solved] Determine the dimensions of the rectangle of the largest area What Are The Dimensions Of The Largest Rectangular The value of y will be given by y = √r2 −(1 √2 r)2 = √1 2 r2 = 1 √2 r. X = 1 √2 r. The perimeter (p) of a rectangle is the sum of all the individual sides of a rectangle, i.e., p = 2x(a+b). The result you need is that for a rectangle with a given. What Are The Dimensions Of The Largest Rectangular.
From www.chegg.com
Solved Find the area of the largest rectangle that can be What Are The Dimensions Of The Largest Rectangular Find the largest possible rectangular area you can enclose, assuming you have 128 meters of fencing. So with a perimeter of 28 feet,. Our dimensions of a rectangle. You should take the dimensions of the rectangle as $2x,2y$ and $2z$ instead of $x,y$ and $z$. Thus the shape will be a square of dimensions 1 √2 r by 1 √2. What Are The Dimensions Of The Largest Rectangular.
From www.youtube.com
Find Dimensions Of Largest Rectangular building that can be placed on a What Are The Dimensions Of The Largest Rectangular The result you need is that for a rectangle with a given perimeter the square has the largest area. X = 1 √2 r. Thus the shape will be a square of dimensions 1 √2 r by 1 √2 r, giving a maximum area of 1 2. The perimeter (p) of a rectangle is the sum of all the individual. What Are The Dimensions Of The Largest Rectangular.