Points Of Inflection Using First Derivative . The second derivative tells us if the slope increases or decreases. Explain the concavity test for a function. Consider a function f f that is continuous over an interval i. using the first derivative test. It's going from positive negative or negative to. so an inflection point are points where our second derivative is switching sides. if i am finding the inflection points of a function using the first derivative graph, i recognize that it exists where the first derivative changes from. Find all critical points of f f and divide the. The derivative of a function gives the slope. sal analyzes the graph of a the derivative g' of function g to find all the inflection. use concavity and inflection points to explain how the sign of the second derivative affects the shape of a function’s graph. When the second derivative is. if f ′ ′ > 0 for all x in i, then the graph of f is concave upward on i. If f ′ ′ < 0 for all x in i, then the graph of f is concave downward on i.”.
from www.easysevens.com
using the first derivative test. If f ′ ′ < 0 for all x in i, then the graph of f is concave downward on i.”. The second derivative tells us if the slope increases or decreases. The derivative of a function gives the slope. When the second derivative is. so an inflection point are points where our second derivative is switching sides. if i am finding the inflection points of a function using the first derivative graph, i recognize that it exists where the first derivative changes from. use concavity and inflection points to explain how the sign of the second derivative affects the shape of a function’s graph. Find all critical points of f f and divide the. if f ′ ′ > 0 for all x in i, then the graph of f is concave upward on i.
Derivatives Local Maximum, Minimum and Point of Inflection
Points Of Inflection Using First Derivative Consider a function f f that is continuous over an interval i. Consider a function f f that is continuous over an interval i. Find all critical points of f f and divide the. The second derivative tells us if the slope increases or decreases. Explain the concavity test for a function. The derivative of a function gives the slope. if i am finding the inflection points of a function using the first derivative graph, i recognize that it exists where the first derivative changes from. if f ′ ′ > 0 for all x in i, then the graph of f is concave upward on i. use concavity and inflection points to explain how the sign of the second derivative affects the shape of a function’s graph. so an inflection point are points where our second derivative is switching sides. sal analyzes the graph of a the derivative g' of function g to find all the inflection. If f ′ ′ < 0 for all x in i, then the graph of f is concave downward on i.”. using the first derivative test. It's going from positive negative or negative to. When the second derivative is.
From dxovkgbnl.blob.core.windows.net
Point Of Inflection And Maximum at Kathleen Rickel blog Points Of Inflection Using First Derivative using the first derivative test. If f ′ ′ < 0 for all x in i, then the graph of f is concave downward on i.”. sal analyzes the graph of a the derivative g' of function g to find all the inflection. It's going from positive negative or negative to. The second derivative tells us if the. Points Of Inflection Using First Derivative.
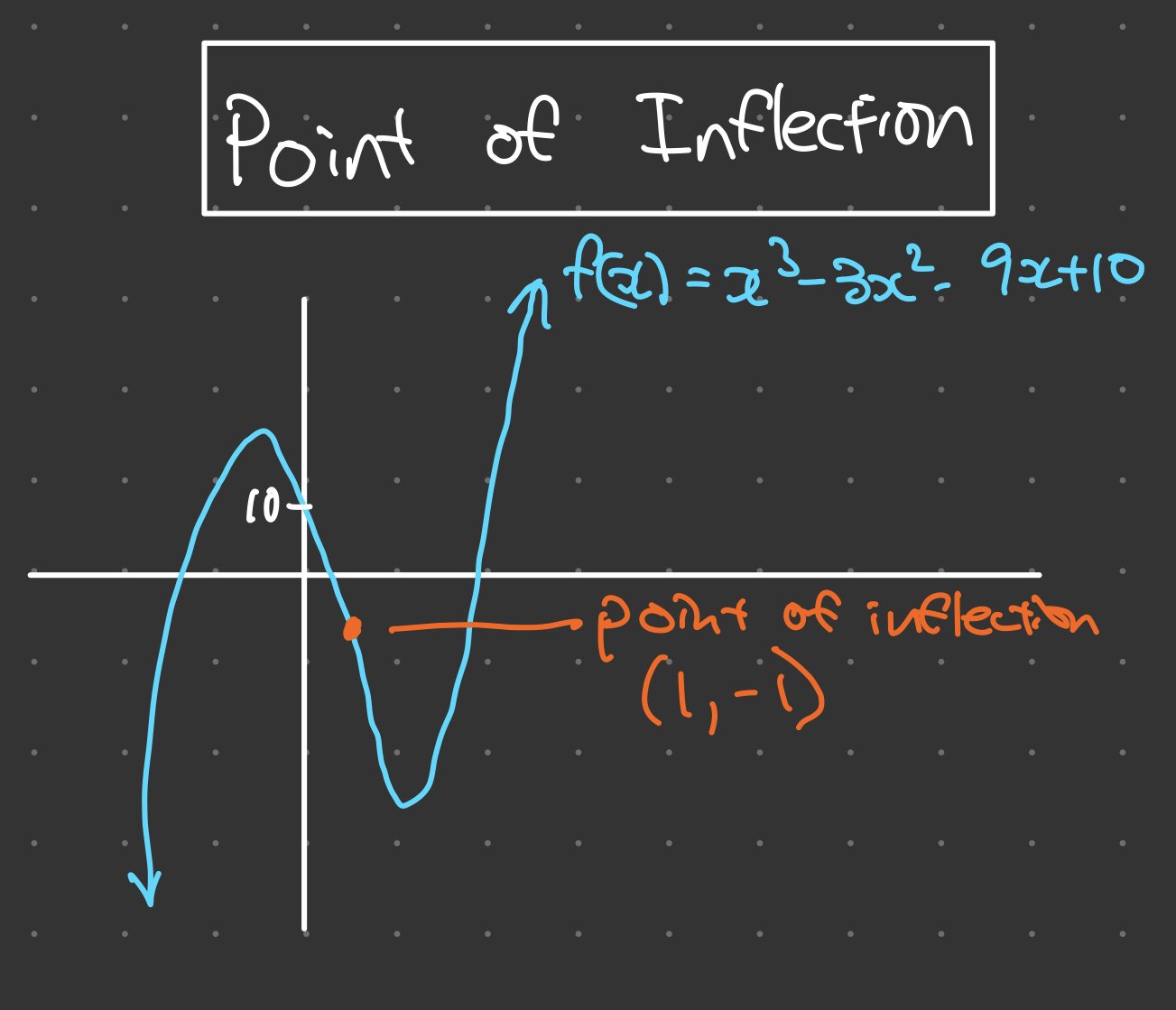
From math.stackexchange.com
calculus Find critical points and inflection points given the Points Of Inflection Using First Derivative if f ′ ′ > 0 for all x in i, then the graph of f is concave upward on i. if i am finding the inflection points of a function using the first derivative graph, i recognize that it exists where the first derivative changes from. so an inflection point are points where our second derivative. Points Of Inflection Using First Derivative.
From www.youtube.com
Inflection points from graphs of function & derivatives AP Calculus Points Of Inflection Using First Derivative so an inflection point are points where our second derivative is switching sides. Consider a function f f that is continuous over an interval i. The second derivative tells us if the slope increases or decreases. if i am finding the inflection points of a function using the first derivative graph, i recognize that it exists where the. Points Of Inflection Using First Derivative.
From www.easysevens.com
Derivatives Local Maximum, Minimum and Point of Inflection Points Of Inflection Using First Derivative The second derivative tells us if the slope increases or decreases. It's going from positive negative or negative to. When the second derivative is. sal analyzes the graph of a the derivative g' of function g to find all the inflection. Explain the concavity test for a function. if f ′ ′ > 0 for all x in. Points Of Inflection Using First Derivative.
From mungfali.com
How To Find Inflection Points Of A Function Points Of Inflection Using First Derivative If f ′ ′ < 0 for all x in i, then the graph of f is concave downward on i.”. so an inflection point are points where our second derivative is switching sides. if f ′ ′ > 0 for all x in i, then the graph of f is concave upward on i. The derivative of. Points Of Inflection Using First Derivative.
From www.slideserve.com
PPT First Derivative Test, Concavity, Points of Inflection PowerPoint Points Of Inflection Using First Derivative if i am finding the inflection points of a function using the first derivative graph, i recognize that it exists where the first derivative changes from. so an inflection point are points where our second derivative is switching sides. If f ′ ′ < 0 for all x in i, then the graph of f is concave downward. Points Of Inflection Using First Derivative.
From www.youtube.com
Determine Point of Inflection and Sketch Graph from First and Second Points Of Inflection Using First Derivative When the second derivative is. use concavity and inflection points to explain how the sign of the second derivative affects the shape of a function’s graph. The second derivative tells us if the slope increases or decreases. sal analyzes the graph of a the derivative g' of function g to find all the inflection. so an inflection. Points Of Inflection Using First Derivative.
From www.youtube.com
Given a graph of f' learn to find the points of inflection YouTube Points Of Inflection Using First Derivative The derivative of a function gives the slope. Consider a function f f that is continuous over an interval i. If f ′ ′ < 0 for all x in i, then the graph of f is concave downward on i.”. Explain the concavity test for a function. so an inflection point are points where our second derivative is. Points Of Inflection Using First Derivative.
From www.youtube.com
Why do we use first and second derivatives to find stationary points Points Of Inflection Using First Derivative Find all critical points of f f and divide the. sal analyzes the graph of a the derivative g' of function g to find all the inflection. if f ′ ′ > 0 for all x in i, then the graph of f is concave upward on i. Explain the concavity test for a function. if i. Points Of Inflection Using First Derivative.
From www.gauthmath.com
Solved Concavity and points of inflection. Answer the following Points Of Inflection Using First Derivative It's going from positive negative or negative to. sal analyzes the graph of a the derivative g' of function g to find all the inflection. using the first derivative test. if f ′ ′ > 0 for all x in i, then the graph of f is concave upward on i. If f ′ ′ < 0. Points Of Inflection Using First Derivative.
From www.slideserve.com
PPT First Derivative Test, Concavity, Points of Inflection PowerPoint Points Of Inflection Using First Derivative When the second derivative is. using the first derivative test. Consider a function f f that is continuous over an interval i. Explain the concavity test for a function. if i am finding the inflection points of a function using the first derivative graph, i recognize that it exists where the first derivative changes from. so an. Points Of Inflection Using First Derivative.
From satprep.co.in
derivative find (in general) points of inflection on the curve. Points Of Inflection Using First Derivative The second derivative tells us if the slope increases or decreases. so an inflection point are points where our second derivative is switching sides. Consider a function f f that is continuous over an interval i. It's going from positive negative or negative to. If f ′ ′ < 0 for all x in i, then the graph of. Points Of Inflection Using First Derivative.
From www.youtube.com
Calculus I Inflection points from the graph of f'' YouTube Points Of Inflection Using First Derivative if i am finding the inflection points of a function using the first derivative graph, i recognize that it exists where the first derivative changes from. if f ′ ′ > 0 for all x in i, then the graph of f is concave upward on i. so an inflection point are points where our second derivative. Points Of Inflection Using First Derivative.
From www.slideshare.net
IB Maths. Turning points. First derivative test Points Of Inflection Using First Derivative Explain the concavity test for a function. Consider a function f f that is continuous over an interval i. use concavity and inflection points to explain how the sign of the second derivative affects the shape of a function’s graph. Find all critical points of f f and divide the. When the second derivative is. so an inflection. Points Of Inflection Using First Derivative.
From www.showme.com
Points of inflection Math, Calculus, Derivatives and Differentiation Points Of Inflection Using First Derivative When the second derivative is. If f ′ ′ < 0 for all x in i, then the graph of f is concave downward on i.”. Find all critical points of f f and divide the. The derivative of a function gives the slope. sal analyzes the graph of a the derivative g' of function g to find all. Points Of Inflection Using First Derivative.
From slideplayer.com
5.3 Using Derivatives for Curve Sketching ppt download Points Of Inflection Using First Derivative When the second derivative is. sal analyzes the graph of a the derivative g' of function g to find all the inflection. Explain the concavity test for a function. The derivative of a function gives the slope. Consider a function f f that is continuous over an interval i. so an inflection point are points where our second. Points Of Inflection Using First Derivative.
From calcworkshop.com
The Second Derivative Test (HowTo w/ 15 StepbyStep Examples!) Points Of Inflection Using First Derivative The second derivative tells us if the slope increases or decreases. Find all critical points of f f and divide the. When the second derivative is. if f ′ ′ > 0 for all x in i, then the graph of f is concave upward on i. sal analyzes the graph of a the derivative g' of function. Points Of Inflection Using First Derivative.
From www.nagwa.com
Question Video Finding the Inflection Point of a Function Using the Points Of Inflection Using First Derivative It's going from positive negative or negative to. sal analyzes the graph of a the derivative g' of function g to find all the inflection. If f ′ ′ < 0 for all x in i, then the graph of f is concave downward on i.”. use concavity and inflection points to explain how the sign of the. Points Of Inflection Using First Derivative.
From www.numerade.com
SOLVEDThe graph of /' {) (FIRST DERIVATIVE) is given How many Points Of Inflection Using First Derivative The derivative of a function gives the slope. use concavity and inflection points to explain how the sign of the second derivative affects the shape of a function’s graph. if f ′ ′ > 0 for all x in i, then the graph of f is concave upward on i. If f ′ ′ < 0 for all. Points Of Inflection Using First Derivative.
From en.ppt-online.org
Using first derivative. Using second derivative online presentation Points Of Inflection Using First Derivative so an inflection point are points where our second derivative is switching sides. Find all critical points of f f and divide the. Consider a function f f that is continuous over an interval i. using the first derivative test. The derivative of a function gives the slope. If f ′ ′ < 0 for all x in. Points Of Inflection Using First Derivative.
From www.slideserve.com
PPT First Derivative Test, Concavity, Points of Inflection PowerPoint Points Of Inflection Using First Derivative The second derivative tells us if the slope increases or decreases. Explain the concavity test for a function. It's going from positive negative or negative to. The derivative of a function gives the slope. if i am finding the inflection points of a function using the first derivative graph, i recognize that it exists where the first derivative changes. Points Of Inflection Using First Derivative.
From www.youtube.com
17. Inflection Point First Derivative Test (Somali) YouTube Points Of Inflection Using First Derivative using the first derivative test. The derivative of a function gives the slope. if f ′ ′ > 0 for all x in i, then the graph of f is concave upward on i. if i am finding the inflection points of a function using the first derivative graph, i recognize that it exists where the first. Points Of Inflection Using First Derivative.
From www.researchgate.net
(PDF) Determination of an inflection point for a dosimetric analysis of Points Of Inflection Using First Derivative if f ′ ′ > 0 for all x in i, then the graph of f is concave upward on i. Explain the concavity test for a function. use concavity and inflection points to explain how the sign of the second derivative affects the shape of a function’s graph. The second derivative tells us if the slope increases. Points Of Inflection Using First Derivative.
From www.youtube.com
Concavity and point of Inflection using first and second derivative Points Of Inflection Using First Derivative so an inflection point are points where our second derivative is switching sides. using the first derivative test. sal analyzes the graph of a the derivative g' of function g to find all the inflection. When the second derivative is. use concavity and inflection points to explain how the sign of the second derivative affects the. Points Of Inflection Using First Derivative.
From www.slideserve.com
PPT First Derivative Test, Concavity, Points of Inflection PowerPoint Points Of Inflection Using First Derivative Find all critical points of f f and divide the. The second derivative tells us if the slope increases or decreases. if f ′ ′ > 0 for all x in i, then the graph of f is concave upward on i. If f ′ ′ < 0 for all x in i, then the graph of f is. Points Of Inflection Using First Derivative.
From www.wikihow.com
5 Ways to Find Inflection Points wikiHow Points Of Inflection Using First Derivative so an inflection point are points where our second derivative is switching sides. If f ′ ′ < 0 for all x in i, then the graph of f is concave downward on i.”. sal analyzes the graph of a the derivative g' of function g to find all the inflection. if f ′ ′ > 0. Points Of Inflection Using First Derivative.
From mungfali.com
Question Video Finding The 푥coordinates Of The Inflection Points Of A 168 Points Of Inflection Using First Derivative if i am finding the inflection points of a function using the first derivative graph, i recognize that it exists where the first derivative changes from. Explain the concavity test for a function. When the second derivative is. Find all critical points of f f and divide the. so an inflection point are points where our second derivative. Points Of Inflection Using First Derivative.
From www.chegg.com
Solved Use the first derivative to find all critical points Points Of Inflection Using First Derivative If f ′ ′ < 0 for all x in i, then the graph of f is concave downward on i.”. Consider a function f f that is continuous over an interval i. The second derivative tells us if the slope increases or decreases. sal analyzes the graph of a the derivative g' of function g to find all. Points Of Inflection Using First Derivative.
From www.chegg.com
Solved Use the first derivative to find all critical points Points Of Inflection Using First Derivative The second derivative tells us if the slope increases or decreases. Find all critical points of f f and divide the. so an inflection point are points where our second derivative is switching sides. The derivative of a function gives the slope. If f ′ ′ < 0 for all x in i, then the graph of f is. Points Of Inflection Using First Derivative.
From www.youtube.com
Worked example Inflection points from first derivative AP Calculus Points Of Inflection Using First Derivative if f ′ ′ > 0 for all x in i, then the graph of f is concave upward on i. Find all critical points of f f and divide the. When the second derivative is. use concavity and inflection points to explain how the sign of the second derivative affects the shape of a function’s graph. . Points Of Inflection Using First Derivative.
From www.numerade.com
SOLVED The first and second derivatives of the function f(x) have the Points Of Inflection Using First Derivative so an inflection point are points where our second derivative is switching sides. If f ′ ′ < 0 for all x in i, then the graph of f is concave downward on i.”. sal analyzes the graph of a the derivative g' of function g to find all the inflection. Explain the concavity test for a function.. Points Of Inflection Using First Derivative.
From www.chegg.com
Solved a Use the first derivative to find all critical Points Of Inflection Using First Derivative using the first derivative test. Find all critical points of f f and divide the. When the second derivative is. if f ′ ′ > 0 for all x in i, then the graph of f is concave upward on i. Explain the concavity test for a function. The derivative of a function gives the slope. The second. Points Of Inflection Using First Derivative.
From www.slideserve.com
PPT First Derivative Test, Concavity, Points of Inflection PowerPoint Points Of Inflection Using First Derivative using the first derivative test. Explain the concavity test for a function. It's going from positive negative or negative to. Find all critical points of f f and divide the. if i am finding the inflection points of a function using the first derivative graph, i recognize that it exists where the first derivative changes from. If f. Points Of Inflection Using First Derivative.
From www.reddit.com
[College Calculus] Without a given equation, how do I find the points Points Of Inflection Using First Derivative use concavity and inflection points to explain how the sign of the second derivative affects the shape of a function’s graph. if f ′ ′ > 0 for all x in i, then the graph of f is concave upward on i. It's going from positive negative or negative to. When the second derivative is. Explain the concavity. Points Of Inflection Using First Derivative.
From www.slideserve.com
PPT First Derivative Test, Concavity, Points of Inflection PowerPoint Points Of Inflection Using First Derivative If f ′ ′ < 0 for all x in i, then the graph of f is concave downward on i.”. Find all critical points of f f and divide the. if i am finding the inflection points of a function using the first derivative graph, i recognize that it exists where the first derivative changes from. if. Points Of Inflection Using First Derivative.