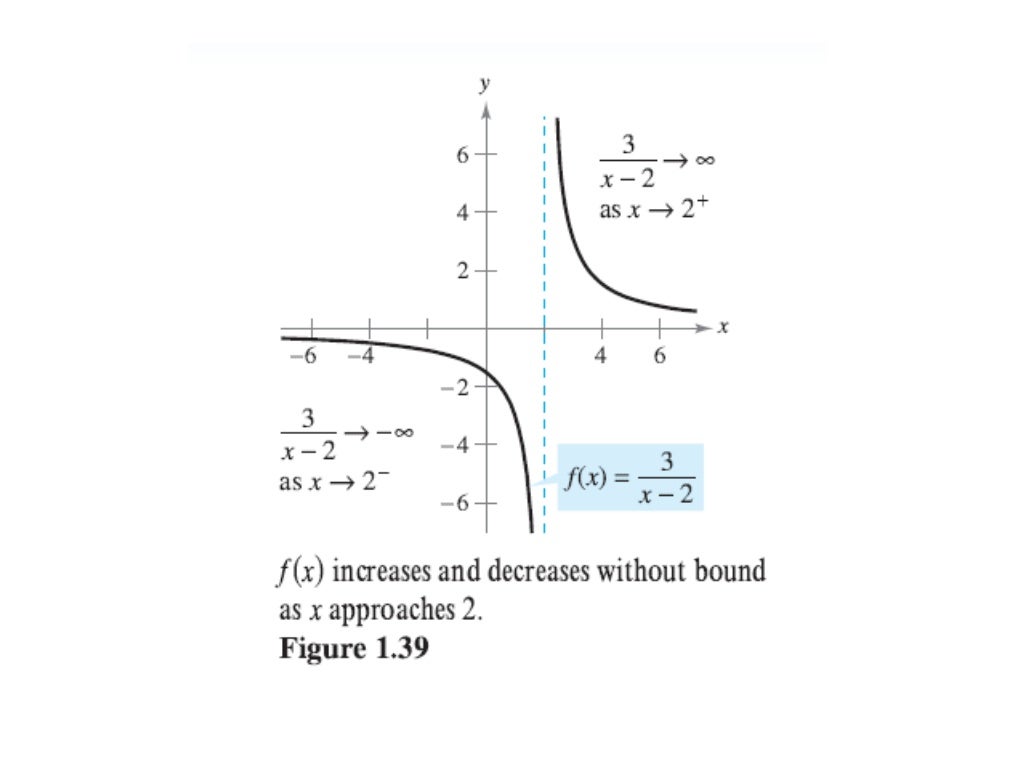
Horizontal And Vertical Asymptotes Using Limits at Alexandra Donohoe blog

Horizontal And Vertical Asymptotes Using Limits. This makes finding horizontal limits of rational functions much easier. A line \(x=a\) is a vertical asymptote if at least one of the. Calculate the limit of a function as [latex]x[/latex] increases or decreases without bound. A line \(y=l\) is a horizontal asymptote of \(f\) if the limit as \(x→∞\) or the limit as \(x→−∞\) of \(f(x)\) is \(l\). Using correct notation, describe an infinite limit. Then we study the idea of a function with an infinite limit. As the name suggests, in addition to horizontal asymptotes we can also. We begin by examining what it means for a function to have a finite limit at infinity. If the limit of a function f(x) at v is infinite, there is a vertical asymptote at x=v. This means that f(x) approaches negative or positive infinity as x approaches v. The graph of f(x) = (cosx) / x + 1 crosses its horizontal asymptote y = 1 an infinite number of times.

Calculate the limit of a function as [latex]x[/latex] increases or decreases without bound. As the name suggests, in addition to horizontal asymptotes we can also. Then we study the idea of a function with an infinite limit. We begin by examining what it means for a function to have a finite limit at infinity. This means that f(x) approaches negative or positive infinity as x approaches v. The graph of f(x) = (cosx) / x + 1 crosses its horizontal asymptote y = 1 an infinite number of times. Using correct notation, describe an infinite limit. A line \(y=l\) is a horizontal asymptote of \(f\) if the limit as \(x→∞\) or the limit as \(x→−∞\) of \(f(x)\) is \(l\). If the limit of a function f(x) at v is infinite, there is a vertical asymptote at x=v. A line \(x=a\) is a vertical asymptote if at least one of the.

Limits & infinity (horizontal & vertical asymptotes) AP Calc

Horizontal And Vertical Asymptotes Using Limits A line \(y=l\) is a horizontal asymptote of \(f\) if the limit as \(x→∞\) or the limit as \(x→−∞\) of \(f(x)\) is \(l\). The graph of f(x) = (cosx) / x + 1 crosses its horizontal asymptote y = 1 an infinite number of times. This means that f(x) approaches negative or positive infinity as x approaches v. If the limit of a function f(x) at v is infinite, there is a vertical asymptote at x=v. Calculate the limit of a function as [latex]x[/latex] increases or decreases without bound. As the name suggests, in addition to horizontal asymptotes we can also. A line \(x=a\) is a vertical asymptote if at least one of the. Using correct notation, describe an infinite limit. We begin by examining what it means for a function to have a finite limit at infinity. Then we study the idea of a function with an infinite limit. This makes finding horizontal limits of rational functions much easier. A line \(y=l\) is a horizontal asymptote of \(f\) if the limit as \(x→∞\) or the limit as \(x→−∞\) of \(f(x)\) is \(l\).