Rainbow Coloring In Graph Theory

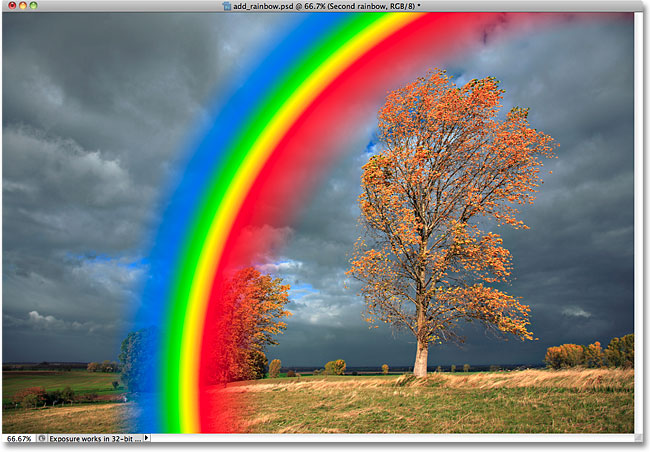
Add A Realistic Rainbow To A Photo With Photoshop

First get a rainbow coloring of the connected dominating set. Then color the remaining edges in such a way that for each vertex x outside there are two disjoint rainbow colored paths (rainbow colored using different set of colors).

Rainbow coloring of a wheel graph, with three colors. Every two non-adjacent vertices can be connected by a rainbow path, either directly through the center vertex (bottom left) or by detouring around one triangle to avoid a repeated edge color (bottom right). In graph theory, a path in an edge.

This then results in a vertex coloring of the graph, often called a rainbow coloring since all vertex colors are distinct. Here, we consider edge colorings of graphs with positive integers such that each vertex color is the average of the colors of its incident edges and all vertex colors are distinct.

The rainbow vertex connection number of a graph G is the smallest number of colors needed in one such coloring and is denoted rvc (G). More recently, Li et al. [12] defined a stronger variant of this problem by requiring that the rainbow paths connecting the pairs of vertices are also shortest paths between those pairs.

Rainbow - Wikiwand

3) Online Rainbow Coloring: In online rainbow coloring, the inputs are a non-trivial un-directed connected simple graph G and a set of colors c. The output is a rainbow colored graph, where there must be atleast one rainbow path between every distinct pair of vertices. Our goal is to use minimum colors while making G rainbow colored. We have constraints such as the edges of G are unknown at.

Abstract - Rainbow vertex coloring introduced a decade ago followed by Rainbow dominator Coloring in recent years has been at tracting the researchers in graph theory. We undertake a study on rainbow vertex coloring and in particular rainbow dominator coloring for specific connected graphs namely Bull graph, Star graph, Complete graph, Helm graph and sunlet graph, Jelly fish, Jewel graph.

An edge color graph G edge- related some two vertices linked different colors. Obviously, graph colourful edge concurrent emotionally concerned. Chapter deals discipline graph theory known diagram coloring. However, some definitions basic concepts graph hypothesis required.

First get a rainbow coloring of the connected dominating set. Then color the remaining edges in such a way that for each vertex x outside there are two disjoint rainbow colored paths (rainbow colored using different set of colors).

In this paper, we introduce three new graph classes, namely tunjung graphs, sandat graphs, and jempiring graphs. We determine the rainbow connection number of the graphs.

This then results in a vertex coloring of the graph, often called a rainbow coloring since all vertex colors are distinct. Here, we consider edge colorings of graphs with positive integers such that each vertex color is the average of the colors of its incident edges and all vertex colors are distinct.

Computing the rainbow connection number of a graph is NP- hard and it finds its applications to the secure transfer of classified information between agencies and scheduling. In this paper the rainbow coloring of double triangular snake DTn was defined and the rainbow connection numbers rc(G) and rvc(G) have been computed.

1 Introduction We will almost entirely focus on coloring edges so "coloring" will mean edge coloring. In most cases, k will be used to denote the number of colors used on the edges. Also define the color degree dc(v) to be the number of colors on edges incident to v. A colored graph is called rainbow if each edge receives a distinct color.

Rainbow ~ Dreamy Nature

In this paper, we introduce three new graph classes, namely tunjung graphs, sandat graphs, and jempiring graphs. We determine the rainbow connection number of the graphs.

An edge color graph G edge- related some two vertices linked different colors. Obviously, graph colourful edge concurrent emotionally concerned. Chapter deals discipline graph theory known diagram coloring. However, some definitions basic concepts graph hypothesis required.

The rainbow vertex connection number of a graph G is the smallest number of colors needed in one such coloring and is denoted rvc (G). More recently, Li et al. [12] defined a stronger variant of this problem by requiring that the rainbow paths connecting the pairs of vertices are also shortest paths between those pairs.

3) Online Rainbow Coloring: In online rainbow coloring, the inputs are a non-trivial un-directed connected simple graph G and a set of colors c. The output is a rainbow colored graph, where there must be atleast one rainbow path between every distinct pair of vertices. Our goal is to use minimum colors while making G rainbow colored. We have constraints such as the edges of G are unknown at.

The Meaning And Symbolism Of The Word - «Rainbow»

An edge color graph G edge- related some two vertices linked different colors. Obviously, graph colourful edge concurrent emotionally concerned. Chapter deals discipline graph theory known diagram coloring. However, some definitions basic concepts graph hypothesis required.

Abstract - Rainbow vertex coloring introduced a decade ago followed by Rainbow dominator Coloring in recent years has been at tracting the researchers in graph theory. We undertake a study on rainbow vertex coloring and in particular rainbow dominator coloring for specific connected graphs namely Bull graph, Star graph, Complete graph, Helm graph and sunlet graph, Jelly fish, Jewel graph.

First get a rainbow coloring of the connected dominating set. Then color the remaining edges in such a way that for each vertex x outside there are two disjoint rainbow colored paths (rainbow colored using different set of colors).

This then results in a vertex coloring of the graph, often called a rainbow coloring since all vertex colors are distinct. Here, we consider edge colorings of graphs with positive integers such that each vertex color is the average of the colors of its incident edges and all vertex colors are distinct.

What Is A Rainbow?

The rainbow vertex connection number of a graph G is the smallest number of colors needed in one such coloring and is denoted rvc (G). More recently, Li et al. [12] defined a stronger variant of this problem by requiring that the rainbow paths connecting the pairs of vertices are also shortest paths between those pairs.

In this paper, we introduce three new graph classes, namely tunjung graphs, sandat graphs, and jempiring graphs. We determine the rainbow connection number of the graphs.

1 Introduction We will almost entirely focus on coloring edges so "coloring" will mean edge coloring. In most cases, k will be used to denote the number of colors used on the edges. Also define the color degree dc(v) to be the number of colors on edges incident to v. A colored graph is called rainbow if each edge receives a distinct color.

This then results in a vertex coloring of the graph, often called a rainbow coloring since all vertex colors are distinct. Here, we consider edge colorings of graphs with positive integers such that each vertex color is the average of the colors of its incident edges and all vertex colors are distinct.

Rainbow - Wikiwand

Abstract - Rainbow vertex coloring introduced a decade ago followed by Rainbow dominator Coloring in recent years has been at tracting the researchers in graph theory. We undertake a study on rainbow vertex coloring and in particular rainbow dominator coloring for specific connected graphs namely Bull graph, Star graph, Complete graph, Helm graph and sunlet graph, Jelly fish, Jewel graph.

This then results in a vertex coloring of the graph, often called a rainbow coloring since all vertex colors are distinct. Here, we consider edge colorings of graphs with positive integers such that each vertex color is the average of the colors of its incident edges and all vertex colors are distinct.

An edge color graph G edge- related some two vertices linked different colors. Obviously, graph colourful edge concurrent emotionally concerned. Chapter deals discipline graph theory known diagram coloring. However, some definitions basic concepts graph hypothesis required.

3) Online Rainbow Coloring: In online rainbow coloring, the inputs are a non-trivial un-directed connected simple graph G and a set of colors c. The output is a rainbow colored graph, where there must be atleast one rainbow path between every distinct pair of vertices. Our goal is to use minimum colors while making G rainbow colored. We have constraints such as the edges of G are unknown at.

OT: Meteorologists Have Weighed Rainbows... | Texas Longhorns Fan ...

Computing the rainbow connection number of a graph is NP- hard and it finds its applications to the secure transfer of classified information between agencies and scheduling. In this paper the rainbow coloring of double triangular snake DTn was defined and the rainbow connection numbers rc(G) and rvc(G) have been computed.

This then results in a vertex coloring of the graph, often called a rainbow coloring since all vertex colors are distinct. Here, we consider edge colorings of graphs with positive integers such that each vertex color is the average of the colors of its incident edges and all vertex colors are distinct.

Rainbow coloring of a wheel graph, with three colors. Every two non-adjacent vertices can be connected by a rainbow path, either directly through the center vertex (bottom left) or by detouring around one triangle to avoid a repeated edge color (bottom right). In graph theory, a path in an edge.

1 Introduction We will almost entirely focus on coloring edges so "coloring" will mean edge coloring. In most cases, k will be used to denote the number of colors used on the edges. Also define the color degree dc(v) to be the number of colors on edges incident to v. A colored graph is called rainbow if each edge receives a distinct color.

The Rainbow Ladies: Rainbow - This Is So Glitter!

An edge color graph G edge- related some two vertices linked different colors. Obviously, graph colourful edge concurrent emotionally concerned. Chapter deals discipline graph theory known diagram coloring. However, some definitions basic concepts graph hypothesis required.

In this paper, we introduce three new graph classes, namely tunjung graphs, sandat graphs, and jempiring graphs. We determine the rainbow connection number of the graphs.

Computing the rainbow connection number of a graph is NP- hard and it finds its applications to the secure transfer of classified information between agencies and scheduling. In this paper the rainbow coloring of double triangular snake DTn was defined and the rainbow connection numbers rc(G) and rvc(G) have been computed.

1 Introduction We will almost entirely focus on coloring edges so "coloring" will mean edge coloring. In most cases, k will be used to denote the number of colors used on the edges. Also define the color degree dc(v) to be the number of colors on edges incident to v. A colored graph is called rainbow if each edge receives a distinct color.

Rainbow Serpent - Mythologica Encyclopedia

First get a rainbow coloring of the connected dominating set. Then color the remaining edges in such a way that for each vertex x outside there are two disjoint rainbow colored paths (rainbow colored using different set of colors).

Abstract - Rainbow vertex coloring introduced a decade ago followed by Rainbow dominator Coloring in recent years has been at tracting the researchers in graph theory. We undertake a study on rainbow vertex coloring and in particular rainbow dominator coloring for specific connected graphs namely Bull graph, Star graph, Complete graph, Helm graph and sunlet graph, Jelly fish, Jewel graph.

Computing the rainbow connection number of a graph is NP- hard and it finds its applications to the secure transfer of classified information between agencies and scheduling. In this paper the rainbow coloring of double triangular snake DTn was defined and the rainbow connection numbers rc(G) and rvc(G) have been computed.

3) Online Rainbow Coloring: In online rainbow coloring, the inputs are a non-trivial un-directed connected simple graph G and a set of colors c. The output is a rainbow colored graph, where there must be atleast one rainbow path between every distinct pair of vertices. Our goal is to use minimum colors while making G rainbow colored. We have constraints such as the edges of G are unknown at.

Building A Colourful Communications Strategy With ALE Rainbow - UC Today

The rainbow vertex connection number of a graph G is the smallest number of colors needed in one such coloring and is denoted rvc (G). More recently, Li et al. [12] defined a stronger variant of this problem by requiring that the rainbow paths connecting the pairs of vertices are also shortest paths between those pairs.

3) Online Rainbow Coloring: In online rainbow coloring, the inputs are a non-trivial un-directed connected simple graph G and a set of colors c. The output is a rainbow colored graph, where there must be atleast one rainbow path between every distinct pair of vertices. Our goal is to use minimum colors while making G rainbow colored. We have constraints such as the edges of G are unknown at.

In this paper, we introduce three new graph classes, namely tunjung graphs, sandat graphs, and jempiring graphs. We determine the rainbow connection number of the graphs.

Rainbow coloring of a wheel graph, with three colors. Every two non-adjacent vertices can be connected by a rainbow path, either directly through the center vertex (bottom left) or by detouring around one triangle to avoid a repeated edge color (bottom right). In graph theory, a path in an edge.

Python Data Types: From Palette Of Rainbow | By Pradnya Bahulekar | Jan ...

Computing the rainbow connection number of a graph is NP- hard and it finds its applications to the secure transfer of classified information between agencies and scheduling. In this paper the rainbow coloring of double triangular snake DTn was defined and the rainbow connection numbers rc(G) and rvc(G) have been computed.

Abstract - Rainbow vertex coloring introduced a decade ago followed by Rainbow dominator Coloring in recent years has been at tracting the researchers in graph theory. We undertake a study on rainbow vertex coloring and in particular rainbow dominator coloring for specific connected graphs namely Bull graph, Star graph, Complete graph, Helm graph and sunlet graph, Jelly fish, Jewel graph.

3) Online Rainbow Coloring: In online rainbow coloring, the inputs are a non-trivial un-directed connected simple graph G and a set of colors c. The output is a rainbow colored graph, where there must be atleast one rainbow path between every distinct pair of vertices. Our goal is to use minimum colors while making G rainbow colored. We have constraints such as the edges of G are unknown at.

1 Introduction We will almost entirely focus on coloring edges so "coloring" will mean edge coloring. In most cases, k will be used to denote the number of colors used on the edges. Also define the color degree dc(v) to be the number of colors on edges incident to v. A colored graph is called rainbow if each edge receives a distinct color.

What Is A Rainbow?

Computing the rainbow connection number of a graph is NP- hard and it finds its applications to the secure transfer of classified information between agencies and scheduling. In this paper the rainbow coloring of double triangular snake DTn was defined and the rainbow connection numbers rc(G) and rvc(G) have been computed.

3) Online Rainbow Coloring: In online rainbow coloring, the inputs are a non-trivial un-directed connected simple graph G and a set of colors c. The output is a rainbow colored graph, where there must be atleast one rainbow path between every distinct pair of vertices. Our goal is to use minimum colors while making G rainbow colored. We have constraints such as the edges of G are unknown at.

An edge color graph G edge- related some two vertices linked different colors. Obviously, graph colourful edge concurrent emotionally concerned. Chapter deals discipline graph theory known diagram coloring. However, some definitions basic concepts graph hypothesis required.

The rainbow vertex connection number of a graph G is the smallest number of colors needed in one such coloring and is denoted rvc (G). More recently, Li et al. [12] defined a stronger variant of this problem by requiring that the rainbow paths connecting the pairs of vertices are also shortest paths between those pairs.

What Is A Rainbow?

Rainbow coloring of a wheel graph, with three colors. Every two non-adjacent vertices can be connected by a rainbow path, either directly through the center vertex (bottom left) or by detouring around one triangle to avoid a repeated edge color (bottom right). In graph theory, a path in an edge.

This then results in a vertex coloring of the graph, often called a rainbow coloring since all vertex colors are distinct. Here, we consider edge colorings of graphs with positive integers such that each vertex color is the average of the colors of its incident edges and all vertex colors are distinct.

An edge color graph G edge- related some two vertices linked different colors. Obviously, graph colourful edge concurrent emotionally concerned. Chapter deals discipline graph theory known diagram coloring. However, some definitions basic concepts graph hypothesis required.

In this paper, we introduce three new graph classes, namely tunjung graphs, sandat graphs, and jempiring graphs. We determine the rainbow connection number of the graphs.

The Myths Of The Rainbow - Faculty Of Science

Abstract - Rainbow vertex coloring introduced a decade ago followed by Rainbow dominator Coloring in recent years has been at tracting the researchers in graph theory. We undertake a study on rainbow vertex coloring and in particular rainbow dominator coloring for specific connected graphs namely Bull graph, Star graph, Complete graph, Helm graph and sunlet graph, Jelly fish, Jewel graph.

1 Introduction We will almost entirely focus on coloring edges so "coloring" will mean edge coloring. In most cases, k will be used to denote the number of colors used on the edges. Also define the color degree dc(v) to be the number of colors on edges incident to v. A colored graph is called rainbow if each edge receives a distinct color.

3) Online Rainbow Coloring: In online rainbow coloring, the inputs are a non-trivial un-directed connected simple graph G and a set of colors c. The output is a rainbow colored graph, where there must be atleast one rainbow path between every distinct pair of vertices. Our goal is to use minimum colors while making G rainbow colored. We have constraints such as the edges of G are unknown at.

First get a rainbow coloring of the connected dominating set. Then color the remaining edges in such a way that for each vertex x outside there are two disjoint rainbow colored paths (rainbow colored using different set of colors).