Kite Formula

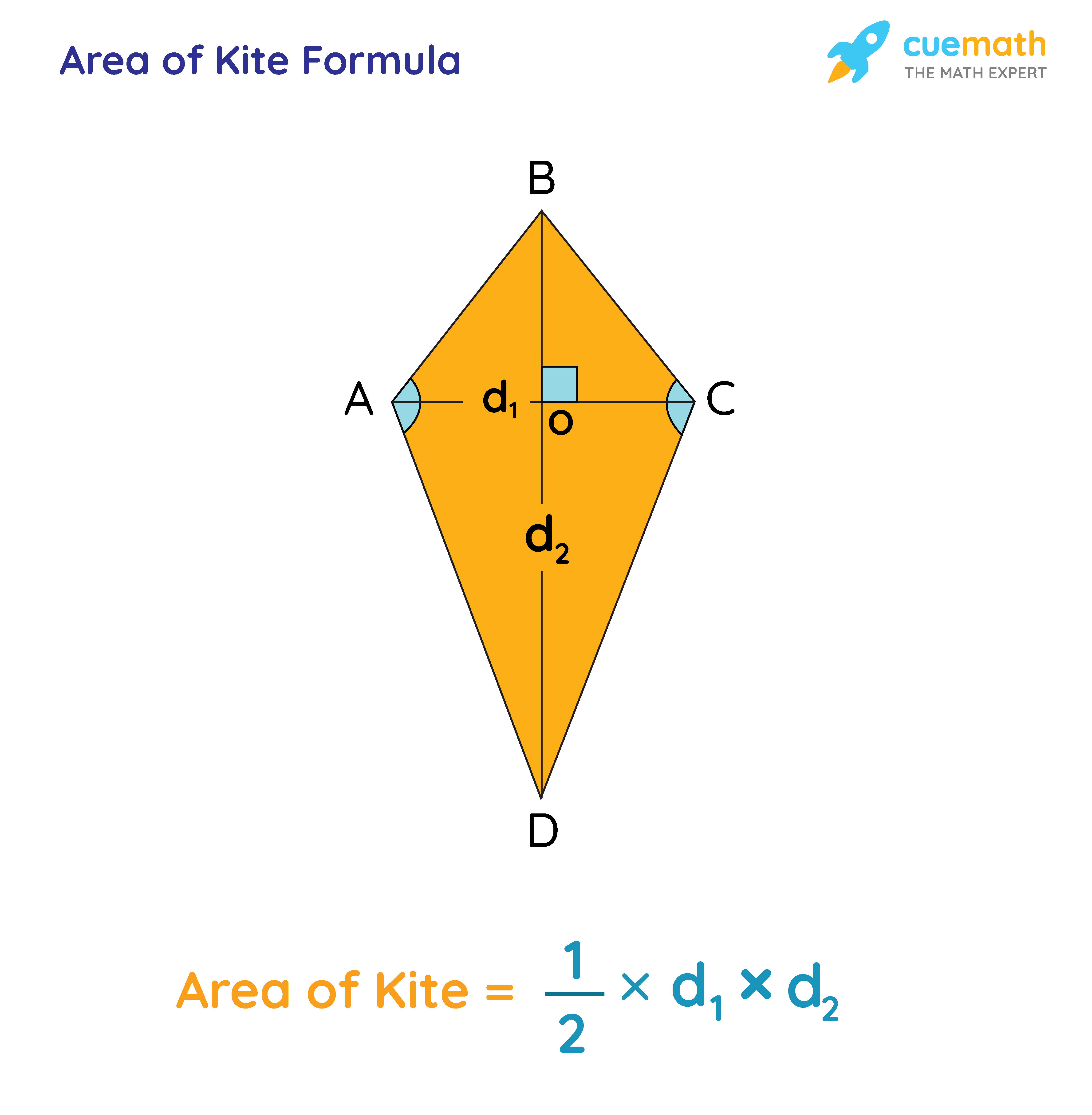
Learn how to find the area of a kite using two formulas: one with diagonals and one with trigonometry. See the definitions, notations, and examples of each formula with Voovers.

The kite area calculator finds the area of a kite if you enter diagonals or two sides and the angle between them. Additionally, it can calculate the kite's perimeter.

Learn how to calculate the area and perimeter of a kite, a flat shape with two pairs of equal-length adjacent sides. See examples, diagrams, and related geometry concepts such as rhombus, square, and dart.

Here is the formula for the area of a kite using the diagonals. Once you know the lengths of the diagonals, you can just multiply them and divide the result by 2. Example #1 Find the area of a kite with diagonals that are 6 inches and 18 inches long. Area = (6 × 18) / 2 = 108 / 2 = 54 square inches. Example #2.

Area Of A Kite - Formula With Examples - Cuemath

A kite is symmetrical about its main diagonal. The shorter diagonal divides the kite into two isosceles triangles. Formula for Area of a Quadrilateral The diagonals of a kite are perpendicular. Area of a kite is given as half of the product of the diagonals which is same as that of a rhombus. Area of a kite can be expressed by the formula: Area.

Learn how to calculate the area of a kite using two methods: the diagonals method and the trigonometry method. See the formula, examples, interactive diagram and other polygon topics.

Learn how to find the area of a kite using two formulas: one with diagonals and one with trigonometry. See the definitions, notations, and examples of each formula with Voovers.

A kite is a type of a quadrilateral that has two pairs of equal, adjacent sides. [1] Kites can take the traditional look of a flying kite, but a kite can also be a rhombus or a square. [2] No matter what a kite looks like, the methods for finding the area will be the same. If you know the length of the diagonals, you can find the area through simple algebra. You can also use trigonometry to.

Area Of A Kite - Formula, Definition, Examples

Learn how to calculate the area of a kite using two methods: the diagonals method and the trigonometry method. See the formula, examples, interactive diagram and other polygon topics.

Question 1. Find the area of a kite whose length of diagonals is 5 cm and 6 cm. Solution: We know the area of a kite is equal to half of the product of both the diagonals. Given, d1 = 5cm and d2 = 6cm Thus, we can write, Area of the kite = 1/2 × 5 × 6 = 5 × 3 = 15 cm2 Question 2. Rahul wants to buy a kite.

Learn what a kite is, its types, and how to calculate its area and perimeter using formulas. See examples of kites with diagrams and solutions.

Learn how to find the area of a kite using two formulas: one with diagonals and one with trigonometry. See the definitions, notations, and examples of each formula with Voovers.

Area Of A Kite Formula

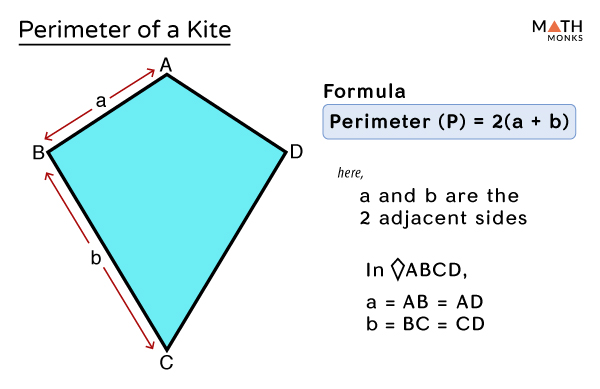
Learn how to calculate the area and perimeter of a kite, a flat shape with two pairs of equal-length adjacent sides. See examples, diagrams, and related geometry concepts such as rhombus, square, and dart.

A kite is a type of a quadrilateral that has two pairs of equal, adjacent sides. [1] Kites can take the traditional look of a flying kite, but a kite can also be a rhombus or a square. [2] No matter what a kite looks like, the methods for finding the area will be the same. If you know the length of the diagonals, you can find the area through simple algebra. You can also use trigonometry to.

Learn what a kite is, its types, and how to calculate its area and perimeter using formulas. See examples of kites with diagrams and solutions.

The diagonals of a kite intersect at 90 $$ ^ {\circ} $$ The formula for the area of a kite is Area = $$ \frac 1 2 $$ (diagonal 1) (diagonal 2).

Perimeter Of A Kite

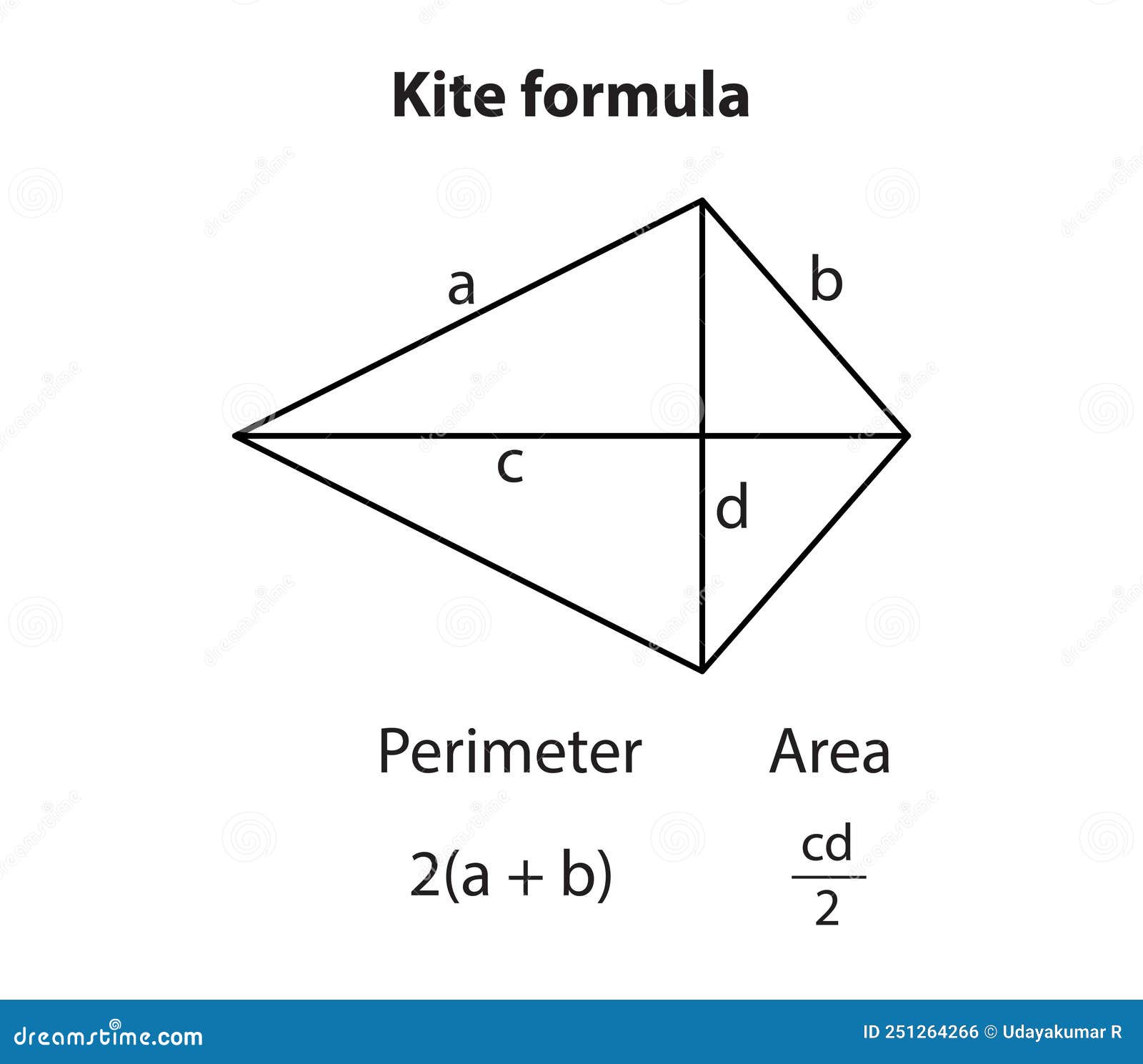
The kite area calculator finds the area of a kite if you enter diagonals or two sides and the angle between them. Additionally, it can calculate the kite's perimeter.

Learn how to calculate the area and perimeter of a kite, a flat shape with two pairs of equal-length adjacent sides. See examples, diagrams, and related geometry concepts such as rhombus, square, and dart.

Learn how to find the area of a kite using two formulas: one with diagonals and one with trigonometry. See the definitions, notations, and examples of each formula with Voovers.

Here is the formula for the area of a kite using the diagonals. Once you know the lengths of the diagonals, you can just multiply them and divide the result by 2. Example #1 Find the area of a kite with diagonals that are 6 inches and 18 inches long. Area = (6 × 18) / 2 = 108 / 2 = 54 square inches. Example #2.

Area Of A Kite - Formulas, Examples And Diagrams

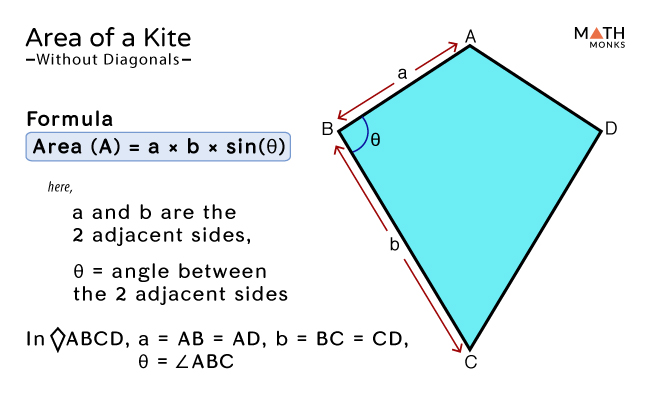
A kite is a type of a quadrilateral that has two pairs of equal, adjacent sides. [1] Kites can take the traditional look of a flying kite, but a kite can also be a rhombus or a square. [2] No matter what a kite looks like, the methods for finding the area will be the same. If you know the length of the diagonals, you can find the area through simple algebra. You can also use trigonometry to.

Learn what a kite is, its types, and how to calculate its area and perimeter using formulas. See examples of kites with diagrams and solutions.

The kite area calculator finds the area of a kite if you enter diagonals or two sides and the angle between them. Additionally, it can calculate the kite's perimeter.

Here is the formula for the area of a kite using the diagonals. Once you know the lengths of the diagonals, you can just multiply them and divide the result by 2. Example #1 Find the area of a kite with diagonals that are 6 inches and 18 inches long. Area = (6 × 18) / 2 = 108 / 2 = 54 square inches. Example #2.

Area Of A Kite (Formulas & Examples) | Free Lesson

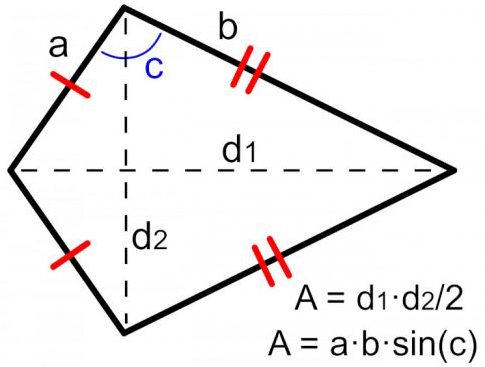
Learn what a kite is, its types, and how to calculate its area and perimeter using formulas. See examples of kites with diagrams and solutions.

Learn how to calculate the area of a kite using two methods: the diagonals method and the trigonometry method. See the formula, examples, interactive diagram and other polygon topics.

Question 1. Find the area of a kite whose length of diagonals is 5 cm and 6 cm. Solution: We know the area of a kite is equal to half of the product of both the diagonals. Given, d1 = 5cm and d2 = 6cm Thus, we can write, Area of the kite = 1/2 × 5 × 6 = 5 × 3 = 15 cm2 Question 2. Rahul wants to buy a kite.

The kite area calculator finds the area of a kite if you enter diagonals or two sides and the angle between them. Additionally, it can calculate the kite's perimeter.

Area Of A Kite - Formulas, Examples And Diagrams

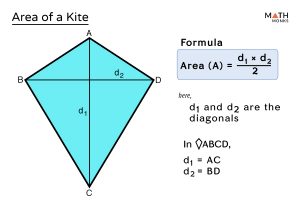
Question 1. Find the area of a kite whose length of diagonals is 5 cm and 6 cm. Solution: We know the area of a kite is equal to half of the product of both the diagonals. Given, d1 = 5cm and d2 = 6cm Thus, we can write, Area of the kite = 1/2 × 5 × 6 = 5 × 3 = 15 cm2 Question 2. Rahul wants to buy a kite.

The kite area calculator finds the area of a kite if you enter diagonals or two sides and the angle between them. Additionally, it can calculate the kite's perimeter.

Learn what a kite is, its types, and how to calculate its area and perimeter using formulas. See examples of kites with diagrams and solutions.

The diagonals of a kite intersect at 90 $$ ^ {\circ} $$ The formula for the area of a kite is Area = $$ \frac 1 2 $$ (diagonal 1) (diagonal 2).

The diagonals of a kite intersect at 90 $$ ^ {\circ} $$ The formula for the area of a kite is Area = $$ \frac 1 2 $$ (diagonal 1) (diagonal 2).

Learn how to calculate the area and perimeter of a kite, a flat shape with two pairs of equal-length adjacent sides. See examples, diagrams, and related geometry concepts such as rhombus, square, and dart.

Learn how to calculate the area of a kite using two methods: the diagonals method and the trigonometry method. See the formula, examples, interactive diagram and other polygon topics.

A kite is a type of a quadrilateral that has two pairs of equal, adjacent sides. [1] Kites can take the traditional look of a flying kite, but a kite can also be a rhombus or a square. [2] No matter what a kite looks like, the methods for finding the area will be the same. If you know the length of the diagonals, you can find the area through simple algebra. You can also use trigonometry to.

Area Of A Kite - YouTube

A kite is symmetrical about its main diagonal. The shorter diagonal divides the kite into two isosceles triangles. Formula for Area of a Quadrilateral The diagonals of a kite are perpendicular. Area of a kite is given as half of the product of the diagonals which is same as that of a rhombus. Area of a kite can be expressed by the formula: Area.

Here is the formula for the area of a kite using the diagonals. Once you know the lengths of the diagonals, you can just multiply them and divide the result by 2. Example #1 Find the area of a kite with diagonals that are 6 inches and 18 inches long. Area = (6 × 18) / 2 = 108 / 2 = 54 square inches. Example #2.

Learn what a kite is, its types, and how to calculate its area and perimeter using formulas. See examples of kites with diagrams and solutions.

Learn how to calculate the area and perimeter of a kite, a flat shape with two pairs of equal-length adjacent sides. See examples, diagrams, and related geometry concepts such as rhombus, square, and dart.

Area And Perimeter Of Kite Formula

Here is the formula for the area of a kite using the diagonals. Once you know the lengths of the diagonals, you can just multiply them and divide the result by 2. Example #1 Find the area of a kite with diagonals that are 6 inches and 18 inches long. Area = (6 × 18) / 2 = 108 / 2 = 54 square inches. Example #2.

A kite is a type of a quadrilateral that has two pairs of equal, adjacent sides. [1] Kites can take the traditional look of a flying kite, but a kite can also be a rhombus or a square. [2] No matter what a kite looks like, the methods for finding the area will be the same. If you know the length of the diagonals, you can find the area through simple algebra. You can also use trigonometry to.

The diagonals of a kite intersect at 90 $$ ^ {\circ} $$ The formula for the area of a kite is Area = $$ \frac 1 2 $$ (diagonal 1) (diagonal 2).

Learn what a kite is, its types, and how to calculate its area and perimeter using formulas. See examples of kites with diagrams and solutions.

Area Of A Kite - Formula With Examples - Cuemath

Learn how to find the area of a kite using two formulas: one with diagonals and one with trigonometry. See the definitions, notations, and examples of each formula with Voovers.

A kite is symmetrical about its main diagonal. The shorter diagonal divides the kite into two isosceles triangles. Formula for Area of a Quadrilateral The diagonals of a kite are perpendicular. Area of a kite is given as half of the product of the diagonals which is same as that of a rhombus. Area of a kite can be expressed by the formula: Area.

A kite is a type of a quadrilateral that has two pairs of equal, adjacent sides. [1] Kites can take the traditional look of a flying kite, but a kite can also be a rhombus or a square. [2] No matter what a kite looks like, the methods for finding the area will be the same. If you know the length of the diagonals, you can find the area through simple algebra. You can also use trigonometry to.

Learn how to calculate the area and perimeter of a kite, a flat shape with two pairs of equal-length adjacent sides. See examples, diagrams, and related geometry concepts such as rhombus, square, and dart.

Kite Formula Area. Geometric Shapes. Isolated On White Background ...

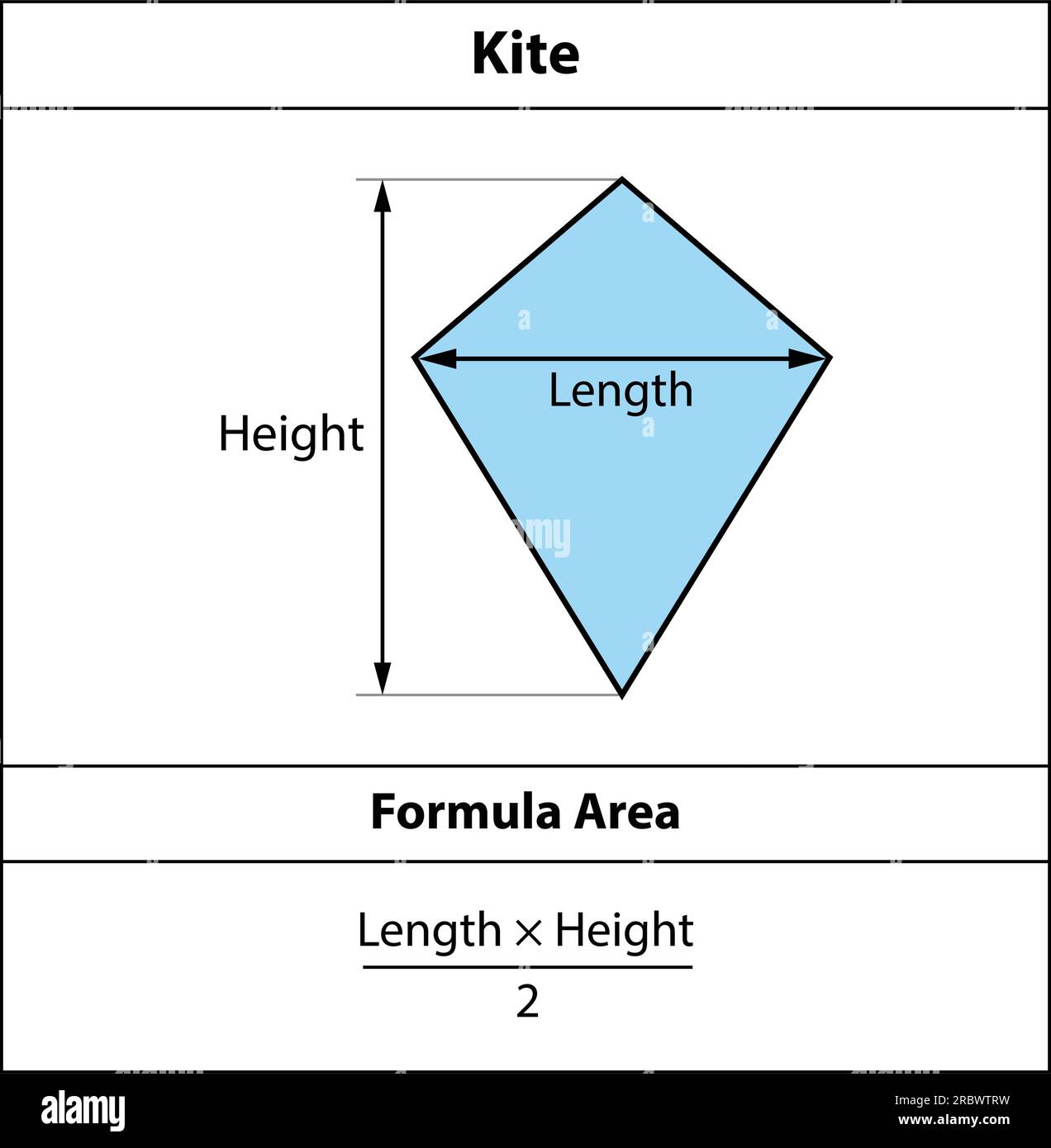
Learn how to find the area of a kite using two formulas: one with diagonals and one with trigonometry. See the definitions, notations, and examples of each formula with Voovers.

The diagonals of a kite intersect at 90 $$ ^ {\circ} $$ The formula for the area of a kite is Area = $$ \frac 1 2 $$ (diagonal 1) (diagonal 2).

Learn how to calculate the area of a kite using two methods: the diagonals method and the trigonometry method. See the formula, examples, interactive diagram and other polygon topics.

The kite area calculator finds the area of a kite if you enter diagonals or two sides and the angle between them. Additionally, it can calculate the kite's perimeter.

Area Of A Kite Formula

The kite area calculator finds the area of a kite if you enter diagonals or two sides and the angle between them. Additionally, it can calculate the kite's perimeter.

The diagonals of a kite intersect at 90 $$ ^ {\circ} $$ The formula for the area of a kite is Area = $$ \frac 1 2 $$ (diagonal 1) (diagonal 2).

Here is the formula for the area of a kite using the diagonals. Once you know the lengths of the diagonals, you can just multiply them and divide the result by 2. Example #1 Find the area of a kite with diagonals that are 6 inches and 18 inches long. Area = (6 × 18) / 2 = 108 / 2 = 54 square inches. Example #2.

Question 1. Find the area of a kite whose length of diagonals is 5 cm and 6 cm. Solution: We know the area of a kite is equal to half of the product of both the diagonals. Given, d1 = 5cm and d2 = 6cm Thus, we can write, Area of the kite = 1/2 × 5 × 6 = 5 × 3 = 15 cm2 Question 2. Rahul wants to buy a kite.

Area Of A Kite Calculator

A kite is a type of a quadrilateral that has two pairs of equal, adjacent sides. [1] Kites can take the traditional look of a flying kite, but a kite can also be a rhombus or a square. [2] No matter what a kite looks like, the methods for finding the area will be the same. If you know the length of the diagonals, you can find the area through simple algebra. You can also use trigonometry to.

Here is the formula for the area of a kite using the diagonals. Once you know the lengths of the diagonals, you can just multiply them and divide the result by 2. Example #1 Find the area of a kite with diagonals that are 6 inches and 18 inches long. Area = (6 × 18) / 2 = 108 / 2 = 54 square inches. Example #2.

Learn how to find the area of a kite using two formulas: one with diagonals and one with trigonometry. See the definitions, notations, and examples of each formula with Voovers.

Learn how to calculate the area of a kite using two methods: the diagonals method and the trigonometry method. See the formula, examples, interactive diagram and other polygon topics.