Fractals Simple Explanation
Fractals represent complex mathematical objects that have been extensively studied as well as depicted by mathematicians, artists, and scientists because of their repetitive features. Referring to the shapes that are different from the simple geometric forms, fractals possess one unique feature that is called self-similarity, and what this means is that each and every part of it is in some way.
What are Fractals? A fractal is a never-ending pattern. Fractals are infinitely complex patterns that are self-similar across different scales. They are created by repeating a simple process over and over in an ongoing feedback loop. Driven by recursion, fractals are images of dynamic systems.
Fractal, in mathematics, any of a class of complex geometric shapes that commonly have "fractional dimension," a concept first introduced by the mathematician Felix Hausdorff in 1918. Fractals are distinct from the simple figures of classical, or Euclidean, geometry-the square, the circle, the.
Or, try a web search for fractal music and you will find music people have created using fractals. Instead of creating images, they create self-similar, repeating patterns with musical notes. Just like when looking at fractal images, when listening to fractal music, it's often easy to forget it was made from a set of mathematical equations!
What Is A Fractal?

Fractals represent complex mathematical objects that have been extensively studied as well as depicted by mathematicians, artists, and scientists because of their repetitive features. Referring to the shapes that are different from the simple geometric forms, fractals possess one unique feature that is called self-similarity, and what this means is that each and every part of it is in some way.
Fractal, in mathematics, any of a class of complex geometric shapes that commonly have "fractional dimension," a concept first introduced by the mathematician Felix Hausdorff in 1918. Fractals are distinct from the simple figures of classical, or Euclidean, geometry-the square, the circle, the.
Or, try a web search for fractal music and you will find music people have created using fractals. Instead of creating images, they create self-similar, repeating patterns with musical notes. Just like when looking at fractal images, when listening to fractal music, it's often easy to forget it was made from a set of mathematical equations!
Fractals have been around forever but were only defined in the last quarter of the 20th century. Think you can wrap your brain around how fractals work?
What Is A Fractal? - The Ultimate Guide To Understanding Fractals
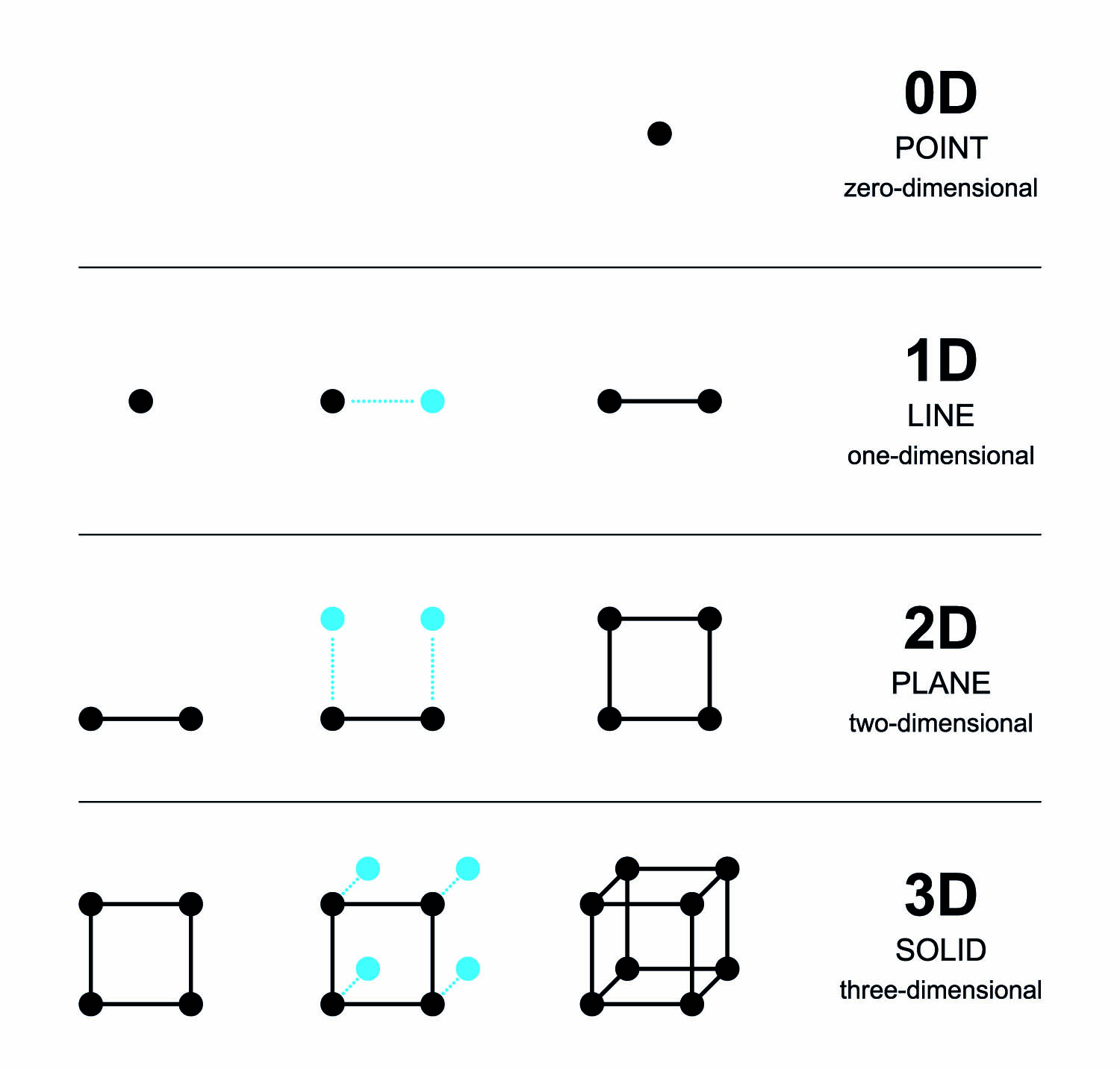
Or, try a web search for fractal music and you will find music people have created using fractals. Instead of creating images, they create self-similar, repeating patterns with musical notes. Just like when looking at fractal images, when listening to fractal music, it's often easy to forget it was made from a set of mathematical equations!
Fractals have been around forever but were only defined in the last quarter of the 20th century. Think you can wrap your brain around how fractals work?
Fractal, in mathematics, any of a class of complex geometric shapes that commonly have "fractional dimension," a concept first introduced by the mathematician Felix Hausdorff in 1918. Fractals are distinct from the simple figures of classical, or Euclidean, geometry-the square, the circle, the.
The definition of fractal goes beyond self-similarity per se to exclude trivial self-similarity and include the idea of a detailed pattern repeating itself. Widely studied fractal sets are the Mandelbrot, Julia, and Newton sets.
Fractals In Math - Definition, Types, & Examples
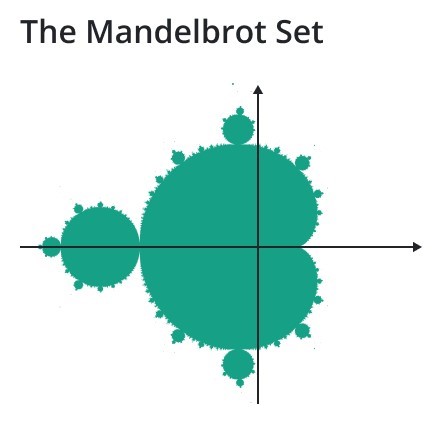
The definition of fractal goes beyond self-similarity per se to exclude trivial self-similarity and include the idea of a detailed pattern repeating itself. Widely studied fractal sets are the Mandelbrot, Julia, and Newton sets.
Fractals represent complex mathematical objects that have been extensively studied as well as depicted by mathematicians, artists, and scientists because of their repetitive features. Referring to the shapes that are different from the simple geometric forms, fractals possess one unique feature that is called self-similarity, and what this means is that each and every part of it is in some way.
What are Fractals? A fractal is a never-ending pattern. Fractals are infinitely complex patterns that are self-similar across different scales. They are created by repeating a simple process over and over in an ongoing feedback loop. Driven by recursion, fractals are images of dynamic systems.
Fractals have been around forever but were only defined in the last quarter of the 20th century. Think you can wrap your brain around how fractals work?

Fractals represent complex mathematical objects that have been extensively studied as well as depicted by mathematicians, artists, and scientists because of their repetitive features. Referring to the shapes that are different from the simple geometric forms, fractals possess one unique feature that is called self-similarity, and what this means is that each and every part of it is in some way.
What are Fractals? A fractal is a never-ending pattern. Fractals are infinitely complex patterns that are self-similar across different scales. They are created by repeating a simple process over and over in an ongoing feedback loop. Driven by recursion, fractals are images of dynamic systems.
It contains a few difficult terminologies, so let's understand it in a simple way. Basically, fractals are shapes which no matter how much you zoom in or zoom out, look similar to the original.
Fractal geometry deals with complexity and irregularity. While on the other hand, traditional Euclidean geometry, deals primarily with simple shapes such as circles, squares, and triangles.
Simple Fractal Concept | Fractals, Art, Fun Math

A simple fractal tree A fractal "tree" to eleven iterations The word "fractal" often has different connotations for mathematicians and the general public, where the public is more likely to be familiar with fractal art than the mathematical concept. The mathematical concept is difficult to define formally, even for mathematicians, but key features can be understood with a little mathematical.
Fractals have been around forever but were only defined in the last quarter of the 20th century. Think you can wrap your brain around how fractals work?
It contains a few difficult terminologies, so let's understand it in a simple way. Basically, fractals are shapes which no matter how much you zoom in or zoom out, look similar to the original.
Fractals represent complex mathematical objects that have been extensively studied as well as depicted by mathematicians, artists, and scientists because of their repetitive features. Referring to the shapes that are different from the simple geometric forms, fractals possess one unique feature that is called self-similarity, and what this means is that each and every part of it is in some way.
How To Draw Fractals By Hand: A Beginner's Guide
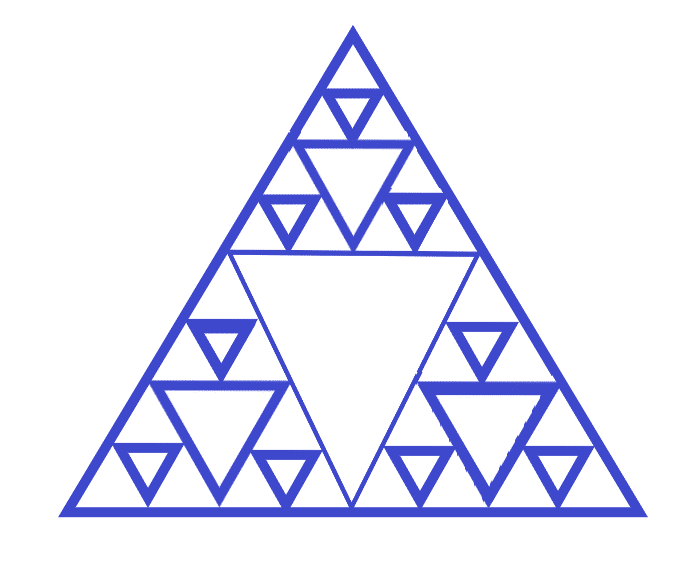
Many things in the real world are like fractals: trees, shorelines, broccoli, lungs, ocean surface, etc. (Note: the name "fractal" comes from the more technical definition involving "fractional dimensions"!).
It contains a few difficult terminologies, so let's understand it in a simple way. Basically, fractals are shapes which no matter how much you zoom in or zoom out, look similar to the original.
Fractals have been around forever but were only defined in the last quarter of the 20th century. Think you can wrap your brain around how fractals work?
Fractals represent complex mathematical objects that have been extensively studied as well as depicted by mathematicians, artists, and scientists because of their repetitive features. Referring to the shapes that are different from the simple geometric forms, fractals possess one unique feature that is called self-similarity, and what this means is that each and every part of it is in some way.
Fractals In Math - Definition, Types, & Examples
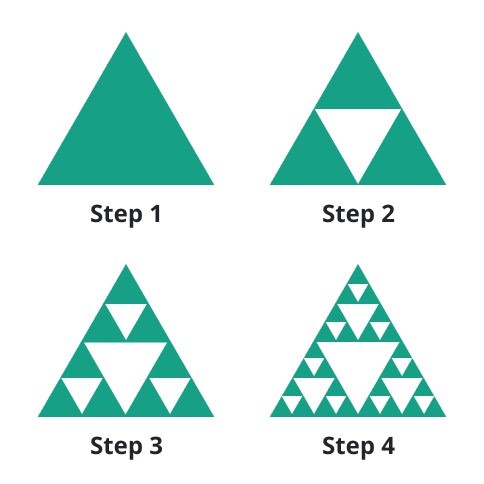
Many things in the real world are like fractals: trees, shorelines, broccoli, lungs, ocean surface, etc. (Note: the name "fractal" comes from the more technical definition involving "fractional dimensions"!).
Or, try a web search for fractal music and you will find music people have created using fractals. Instead of creating images, they create self-similar, repeating patterns with musical notes. Just like when looking at fractal images, when listening to fractal music, it's often easy to forget it was made from a set of mathematical equations!
Fractals have been around forever but were only defined in the last quarter of the 20th century. Think you can wrap your brain around how fractals work?
Fractal geometry deals with complexity and irregularity. While on the other hand, traditional Euclidean geometry, deals primarily with simple shapes such as circles, squares, and triangles.
What Is A Fractal? - The Ultimate Guide To Understanding Fractals

Fractals represent complex mathematical objects that have been extensively studied as well as depicted by mathematicians, artists, and scientists because of their repetitive features. Referring to the shapes that are different from the simple geometric forms, fractals possess one unique feature that is called self-similarity, and what this means is that each and every part of it is in some way.
Or, try a web search for fractal music and you will find music people have created using fractals. Instead of creating images, they create self-similar, repeating patterns with musical notes. Just like when looking at fractal images, when listening to fractal music, it's often easy to forget it was made from a set of mathematical equations!
It contains a few difficult terminologies, so let's understand it in a simple way. Basically, fractals are shapes which no matter how much you zoom in or zoom out, look similar to the original.
What are Fractals? A fractal is a never-ending pattern. Fractals are infinitely complex patterns that are self-similar across different scales. They are created by repeating a simple process over and over in an ongoing feedback loop. Driven by recursion, fractals are images of dynamic systems.
Fractals In Math - Definition, Types, & Examples
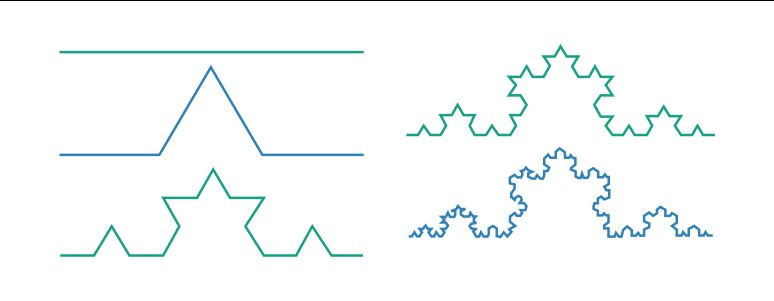
Or, try a web search for fractal music and you will find music people have created using fractals. Instead of creating images, they create self-similar, repeating patterns with musical notes. Just like when looking at fractal images, when listening to fractal music, it's often easy to forget it was made from a set of mathematical equations!
Fractal geometry deals with complexity and irregularity. While on the other hand, traditional Euclidean geometry, deals primarily with simple shapes such as circles, squares, and triangles.
Fractals have been around forever but were only defined in the last quarter of the 20th century. Think you can wrap your brain around how fractals work?
Many things in the real world are like fractals: trees, shorelines, broccoli, lungs, ocean surface, etc. (Note: the name "fractal" comes from the more technical definition involving "fractional dimensions"!).
How To Create A Fractal - Lesson | Study.com

A simple fractal tree A fractal "tree" to eleven iterations The word "fractal" often has different connotations for mathematicians and the general public, where the public is more likely to be familiar with fractal art than the mathematical concept. The mathematical concept is difficult to define formally, even for mathematicians, but key features can be understood with a little mathematical.
Fractal, in mathematics, any of a class of complex geometric shapes that commonly have "fractional dimension," a concept first introduced by the mathematician Felix Hausdorff in 1918. Fractals are distinct from the simple figures of classical, or Euclidean, geometry-the square, the circle, the.
Fractals represent complex mathematical objects that have been extensively studied as well as depicted by mathematicians, artists, and scientists because of their repetitive features. Referring to the shapes that are different from the simple geometric forms, fractals possess one unique feature that is called self-similarity, and what this means is that each and every part of it is in some way.
Many things in the real world are like fractals: trees, shorelines, broccoli, lungs, ocean surface, etc. (Note: the name "fractal" comes from the more technical definition involving "fractional dimensions"!).
Fractals In Math - Definition, Types, & Examples

Or, try a web search for fractal music and you will find music people have created using fractals. Instead of creating images, they create self-similar, repeating patterns with musical notes. Just like when looking at fractal images, when listening to fractal music, it's often easy to forget it was made from a set of mathematical equations!
Fractal geometry deals with complexity and irregularity. While on the other hand, traditional Euclidean geometry, deals primarily with simple shapes such as circles, squares, and triangles.
The definition of fractal goes beyond self-similarity per se to exclude trivial self-similarity and include the idea of a detailed pattern repeating itself. Widely studied fractal sets are the Mandelbrot, Julia, and Newton sets.
What are Fractals? A fractal is a never-ending pattern. Fractals are infinitely complex patterns that are self-similar across different scales. They are created by repeating a simple process over and over in an ongoing feedback loop. Driven by recursion, fractals are images of dynamic systems.
How Fractals Work | HowStuffWorks

A simple fractal tree A fractal "tree" to eleven iterations The word "fractal" often has different connotations for mathematicians and the general public, where the public is more likely to be familiar with fractal art than the mathematical concept. The mathematical concept is difficult to define formally, even for mathematicians, but key features can be understood with a little mathematical.
The definition of fractal goes beyond self-similarity per se to exclude trivial self-similarity and include the idea of a detailed pattern repeating itself. Widely studied fractal sets are the Mandelbrot, Julia, and Newton sets.
Fractals represent complex mathematical objects that have been extensively studied as well as depicted by mathematicians, artists, and scientists because of their repetitive features. Referring to the shapes that are different from the simple geometric forms, fractals possess one unique feature that is called self-similarity, and what this means is that each and every part of it is in some way.
Or, try a web search for fractal music and you will find music people have created using fractals. Instead of creating images, they create self-similar, repeating patterns with musical notes. Just like when looking at fractal images, when listening to fractal music, it's often easy to forget it was made from a set of mathematical equations!

The definition of fractal goes beyond self-similarity per se to exclude trivial self-similarity and include the idea of a detailed pattern repeating itself. Widely studied fractal sets are the Mandelbrot, Julia, and Newton sets.
Fractal, in mathematics, any of a class of complex geometric shapes that commonly have "fractional dimension," a concept first introduced by the mathematician Felix Hausdorff in 1918. Fractals are distinct from the simple figures of classical, or Euclidean, geometry-the square, the circle, the.
Or, try a web search for fractal music and you will find music people have created using fractals. Instead of creating images, they create self-similar, repeating patterns with musical notes. Just like when looking at fractal images, when listening to fractal music, it's often easy to forget it was made from a set of mathematical equations!
It contains a few difficult terminologies, so let's understand it in a simple way. Basically, fractals are shapes which no matter how much you zoom in or zoom out, look similar to the original.
What Is A Fractal? - The Ultimate Guide To Understanding Fractals

Fractals have been around forever but were only defined in the last quarter of the 20th century. Think you can wrap your brain around how fractals work?
Many things in the real world are like fractals: trees, shorelines, broccoli, lungs, ocean surface, etc. (Note: the name "fractal" comes from the more technical definition involving "fractional dimensions"!).
Fractal, in mathematics, any of a class of complex geometric shapes that commonly have "fractional dimension," a concept first introduced by the mathematician Felix Hausdorff in 1918. Fractals are distinct from the simple figures of classical, or Euclidean, geometry-the square, the circle, the.
A simple fractal tree A fractal "tree" to eleven iterations The word "fractal" often has different connotations for mathematicians and the general public, where the public is more likely to be familiar with fractal art than the mathematical concept. The mathematical concept is difficult to define formally, even for mathematicians, but key features can be understood with a little mathematical.
Examples Of Fractal. A Examples Of Mathematical Fractals (Bovill 1996 ...

What are Fractals? A fractal is a never-ending pattern. Fractals are infinitely complex patterns that are self-similar across different scales. They are created by repeating a simple process over and over in an ongoing feedback loop. Driven by recursion, fractals are images of dynamic systems.
It contains a few difficult terminologies, so let's understand it in a simple way. Basically, fractals are shapes which no matter how much you zoom in or zoom out, look similar to the original.
The definition of fractal goes beyond self-similarity per se to exclude trivial self-similarity and include the idea of a detailed pattern repeating itself. Widely studied fractal sets are the Mandelbrot, Julia, and Newton sets.
Many things in the real world are like fractals: trees, shorelines, broccoli, lungs, ocean surface, etc. (Note: the name "fractal" comes from the more technical definition involving "fractional dimensions"!).
Fractal geometry deals with complexity and irregularity. While on the other hand, traditional Euclidean geometry, deals primarily with simple shapes such as circles, squares, and triangles.
A simple fractal tree A fractal "tree" to eleven iterations The word "fractal" often has different connotations for mathematicians and the general public, where the public is more likely to be familiar with fractal art than the mathematical concept. The mathematical concept is difficult to define formally, even for mathematicians, but key features can be understood with a little mathematical.
It contains a few difficult terminologies, so let's understand it in a simple way. Basically, fractals are shapes which no matter how much you zoom in or zoom out, look similar to the original.
Fractal, in mathematics, any of a class of complex geometric shapes that commonly have "fractional dimension," a concept first introduced by the mathematician Felix Hausdorff in 1918. Fractals are distinct from the simple figures of classical, or Euclidean, geometry-the square, the circle, the.
What are Fractals? A fractal is a never-ending pattern. Fractals are infinitely complex patterns that are self-similar across different scales. They are created by repeating a simple process over and over in an ongoing feedback loop. Driven by recursion, fractals are images of dynamic systems.
Many things in the real world are like fractals: trees, shorelines, broccoli, lungs, ocean surface, etc. (Note: the name "fractal" comes from the more technical definition involving "fractional dimensions"!).
Fractals represent complex mathematical objects that have been extensively studied as well as depicted by mathematicians, artists, and scientists because of their repetitive features. Referring to the shapes that are different from the simple geometric forms, fractals possess one unique feature that is called self-similarity, and what this means is that each and every part of it is in some way.
The definition of fractal goes beyond self-similarity per se to exclude trivial self-similarity and include the idea of a detailed pattern repeating itself. Widely studied fractal sets are the Mandelbrot, Julia, and Newton sets.
Or, try a web search for fractal music and you will find music people have created using fractals. Instead of creating images, they create self-similar, repeating patterns with musical notes. Just like when looking at fractal images, when listening to fractal music, it's often easy to forget it was made from a set of mathematical equations!
Fractals have been around forever but were only defined in the last quarter of the 20th century. Think you can wrap your brain around how fractals work?