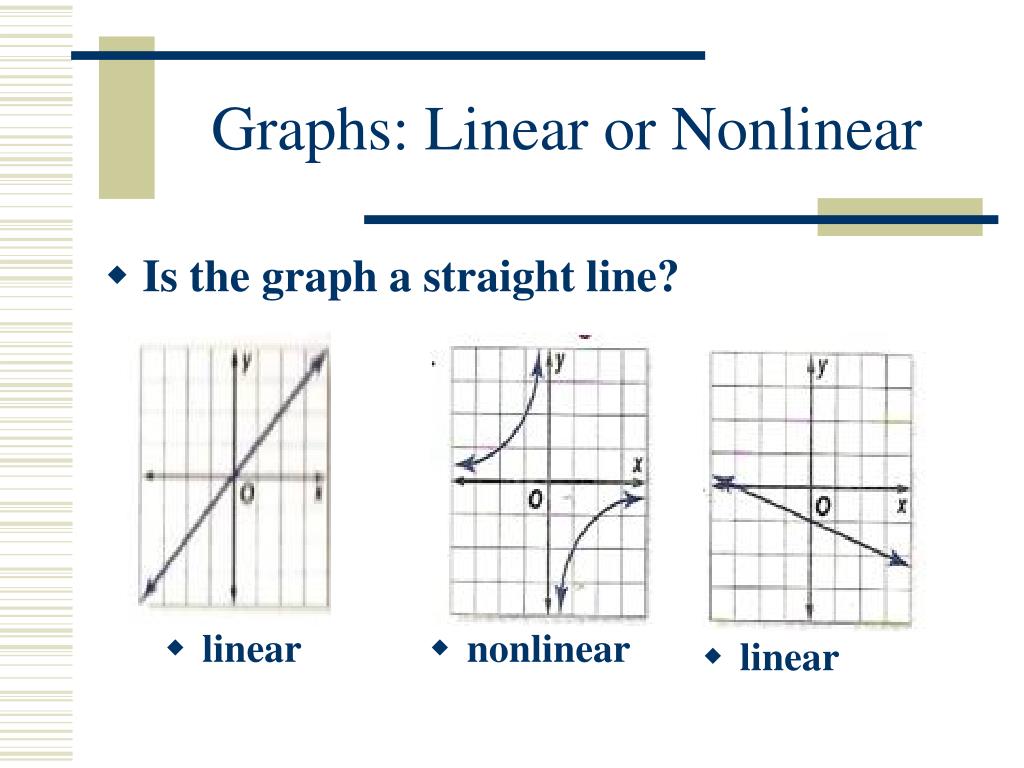
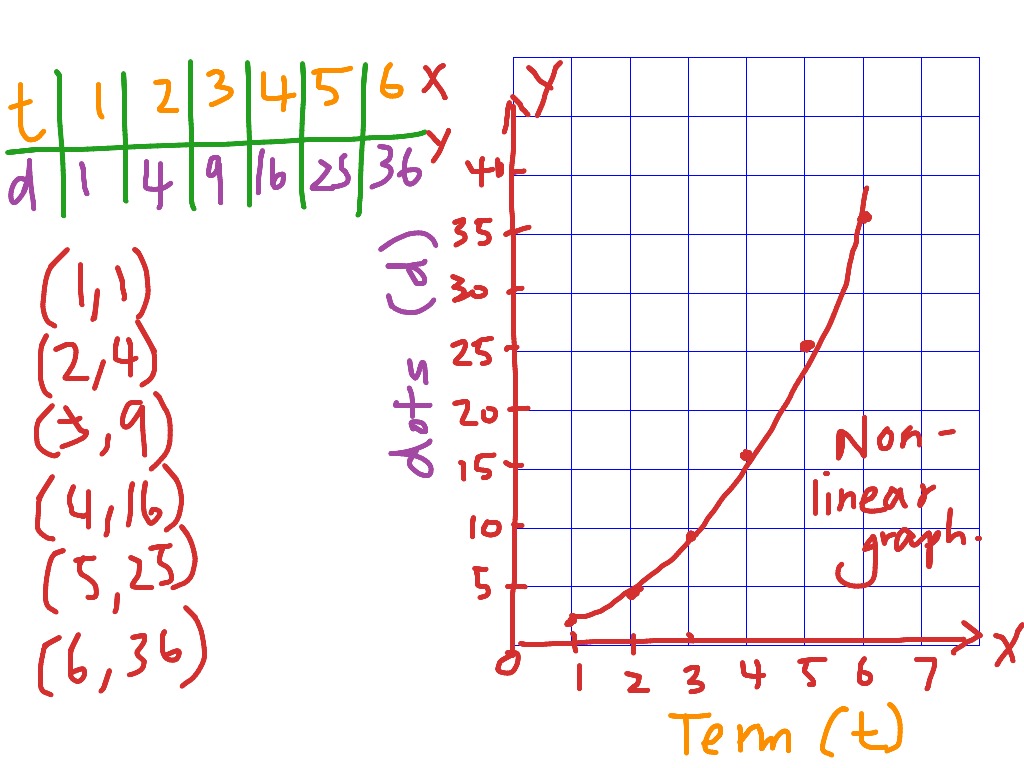
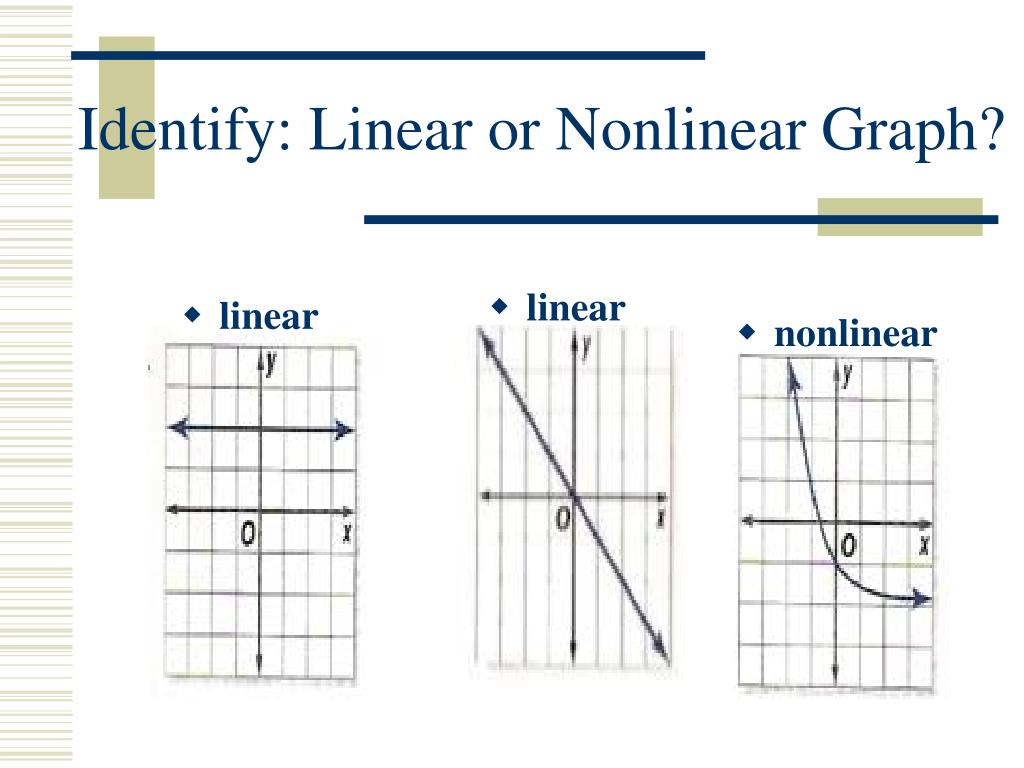
Define Non Linear Graph
A nonlinear function is a function whose graph is not a straight line. i.e., its equation can be anything except of the form f(x) = ax + b. about non linear functions along with non linear graphs.

Learn about non linear functions with simple definitions, key equations, and graph explanations. Explore solved examples to understand how non. Linear vs nonlinear functions is a standard comparison you will encounter while studying mathematics.
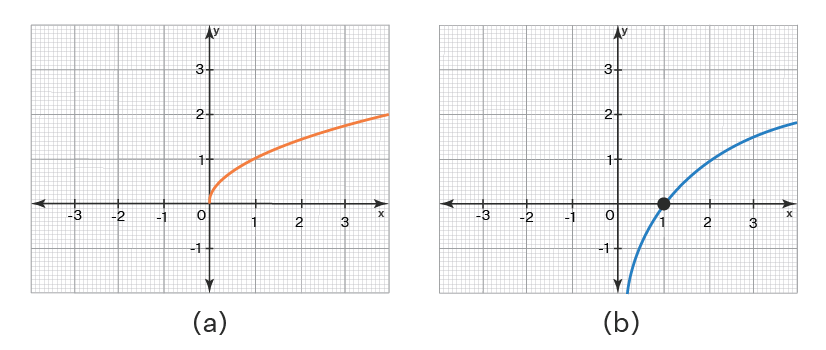
Linear And Non Linear Graphs
Any given function can be represented as a graph. The graph can be linear or nonlinear, depending upon the characteristics of the function. This guide will help you better understand linear and nonlinear functions and how they differ from each other by using many examples and practice questions.
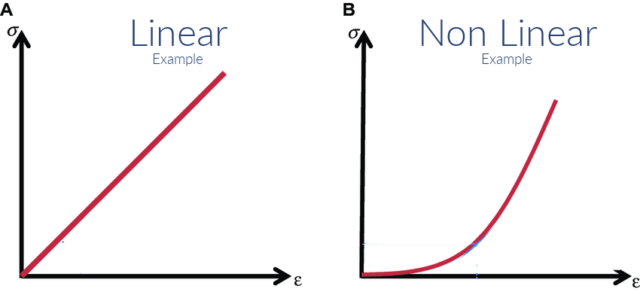
To properly define a nonlinear function, the definition of a linear function is needed. The definition of a linear function is any function that produces a straight line when graphed. A non linear graph shows variable relationships with curves, unlike linear graphs' straight lines.

Introduction to Graphing - ppt download
Learn why non linear graphs are vital for complex analysis. Learn Nonlinear Function at Bytelearn. Know the definitions, see the examples, and practice problems of Nonlinear Function.

Your one. The graph of a linear function is a straight line. The graph of a nonlinear function is a curved line.
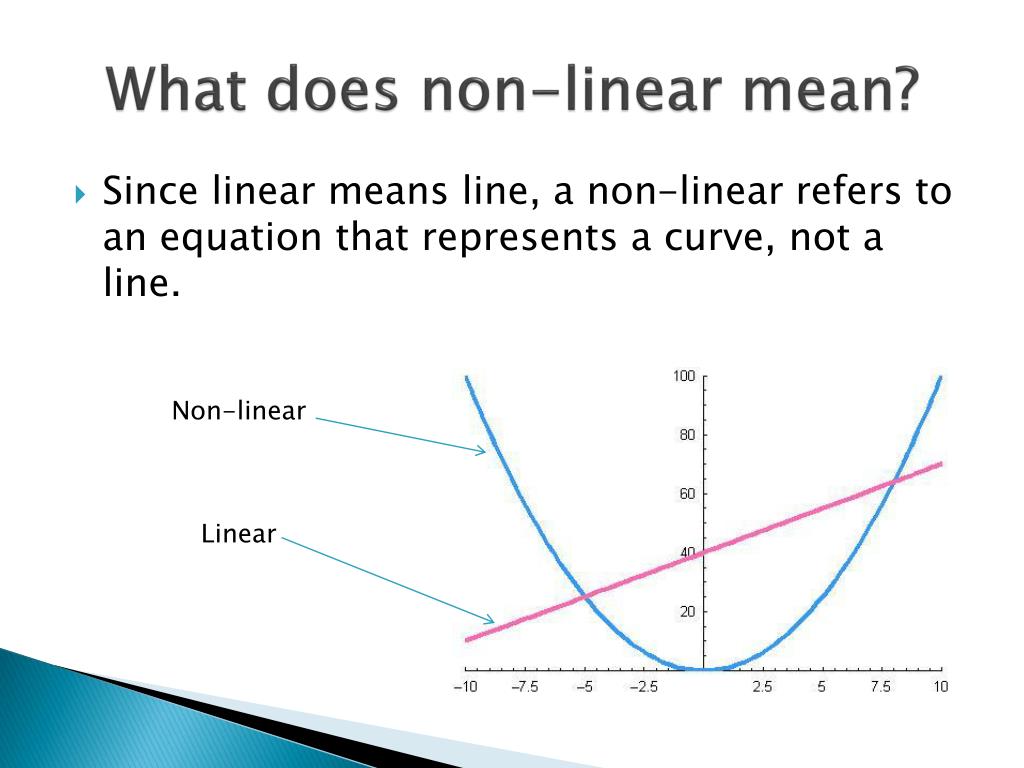
Nonlinear Function
There are many different types of nonlinear functions. Statistics Definitions > Nonlinearity A nonlinearity is a relation between data points that can't be condensed into a neat linear graph. Models of systems such as biochemical reactions in living organisms, combustion and fluid turbulence all show examples of nonlinearities.
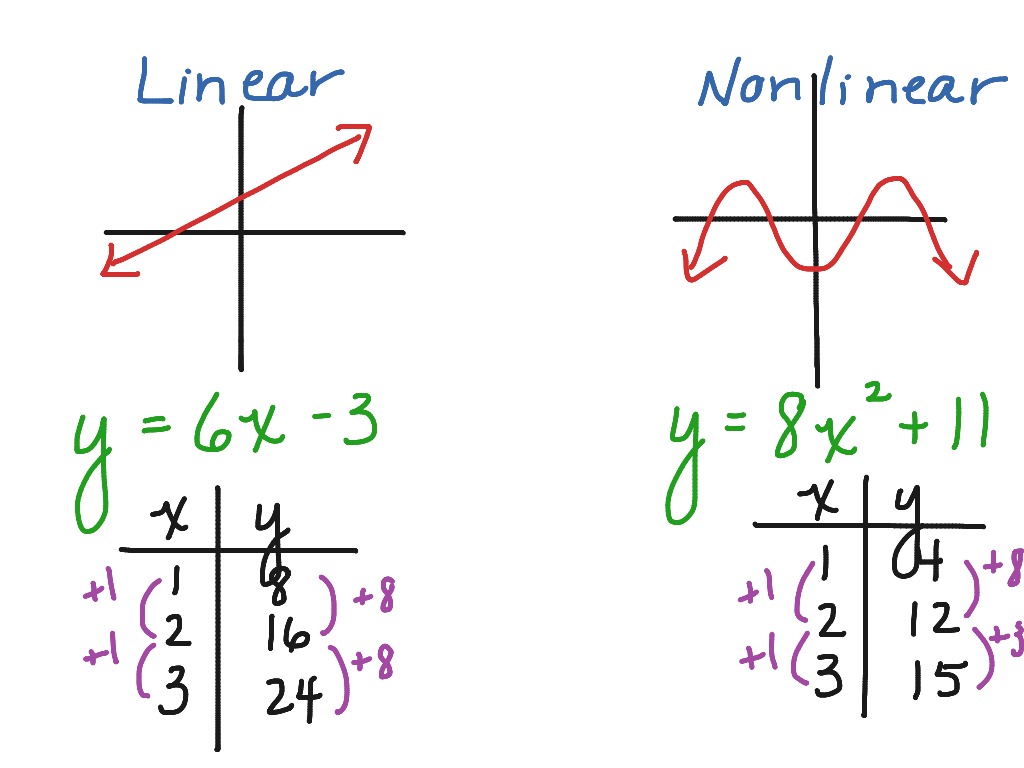
Examples of nonlinear relationships: increasing gradually then rising steeply (red); Decreasing gradually, then. Often in economics a linear function cannot explain the relationship between variables. In such cases a non.

Explore non-linear functions, functions whose graphs are not straight lines. This guide contrasts non-linear functions with linear functions, provides examples of various non-linear functions (quadratic, exponential, etc.), and illustrates their characteristics.