
Lesson: Number Systems
EXERCISE: 1.1
Question: 1
Is zero a rational number? Can you write it in the
form , where P and Q are integers and ?
P
Q
Q 0
Solution:
Yes, zero is a rational number. It is a rational
number as it can be represented as or ect.
0
1
0
2
Question: 2
Find six rational numbers between 3 and 4.
Solution:
There are infinite rational numbers between 3 and 4.
3 and 4 can be represented as and
24
8
32
8
respectively. Therefore, six rational numbers 3 and 4
are:
and
25 26 27 28 29
, , , ,
8 8 8 8 8
30
8

Question: 3
Find five rational numbers between and
3
5
4
5
Solution:
We can find infinite rational numbers between
and
3
5
4
5
3 3 6 18
5 5 6 30
4 4 6 24
5 5 6 30
Therefore, five rational numbers between and
3
5
4
5
are:
are
19 20 21 22
, , ,
30 30 30 30
23
30
Question: 4
State whether the following statements are true or
false. Give reasons for your answers.
(i) Every natural number is a whole number.
(ii) Every integer is a whole number.
(iii) Every rational number is a whole number.

Solution:
(i) True, because natural numbers are part of whole
numbers.
(ii) False, because integers consist of negative
numbers as well as positive numbers while whole
numbers are 0 and positive integers.
As negative integers are not part of whole
numbers, the statement is false.
(iii) False, because rational numbers are of the
form where q is not equal to. So, every
p
q
whole number is a rational numbers but not
vice versa.
EXERCISE: 1.2
Question: 1
State whether the following statements are true or
false. Justify your answers.
(i) Every irrational number is a real number.
(ii) Every point on the number line is of the form √m,
where m is a natural number.
(iii) Every real number is an irrational number.

Solution:
(i) True, because irrational numbers are part of real
numbers.
(ii) False, because points like 0, 0.2, 0.3 etc. and
negative integers, are not of the form √m,
where
m is a natural number.
(iii) False, because real numbers includes rational
numbers and irrational numbers.
Question: 2
Are the square roots of all positive integers
irrational? If not, give an example of the square root
of a number that is a rational number.
Solution:
No, the square roots of all positive integers are not
irrational. For example,
4 2
Question: 3
Show how can be represented on the number line.
5
Solution:
We draw a number line and mark the origin as O.
Assuming OA as 1 unit, we mark the point A on the
right hand side of O.

We draw a right angle OAB such that AB = 2 units.
By Pythagoras theorem,
2 2
OB = OA AB = 1 4 units 5 units. =
We draw a circle with centre O and radius OB. The
circle intersects the number line at C.
units (Radius of the circle)
OB OC 5
The point C represents on the number line
5
EXERCISE: 1.3
Question: 1
Write the following in decimal form and say what
kind of decimal expansion each has:

(i)
36
100
(ii)
1
11
(iii)
1
4
8
(iv)
3
13
(v)
2
11
(vi)
329
400
Solution:
(i) 0.36 (Terminating)
(ii) 0.09090909... (Non-terminating and repeating)
(iii) (Terminating)
1 33
4 4.125
8 8
...0.23076923076
3
13
9iv
(Non - terminating and repeating)
(v) 0.181818181818...
(Non-terminating and repeating)
(vi) (Terminating)
329
0.8225
400

Question: 2
You know that . Can you predict what
0.1 7
1
7
4285
the decimal expansion of are without
2 3 4 5 6
, , , ,
7 7 7 7 7
actually doing the long division? If so, how?
[Hint: Study the remainders while finding the value
of carefully.]
1
7
Solution:
Yes. This can be done by:
2 1
2 2 0.142857 0.285714
7 7
3 1
3 3 0.142857 0.428571
7 7
×
4 1
4 4 0.142857 0.571428
7 7
×
5 1
5 5 0.142857 0.714285
7 7
×
6 1
6 6 0.142857 0.857142
7 7
×

Question: 3
Express the following in the form where and are
p
q
integers and .
0q
(i)
0.6
(ii)
0.47
(iii)
0.001
Solution:
(i)
0.6 0.666...
Let 0.666...x
10 = 6.666... x
10 6 x x
9x = 6
2
=
3
x
(ii)
0.47 0.4777...
=
4 .777...
10 10
Let x = 0.777…
10 = 7.777… x
10 = 7 x x

7
=
9
x
Therefore,
4 .777... 4 7
10 10 10 90
36 7 43
=
90 90
(iii)
0.00100.001 01...
Let
= 0.001001...x
1000 = 1.001001… x
1000 = 1 + x x
999 = 1x
1
=
999
x
Question: 4
Express in the form .
…0.99999
p
q
Are you surprised by your answer? With your
teacher and classmates discuss why the answer
makes sense.
Solution:
Let:
= 0.9999…x
10 = 9.9999…x
10 = 9 + xx

9 = 9x
= 1x
is understood to mean the infinite sum
0.9999... 1
is equal to1”.
...
9 9 9
10 100 1 000
This in turn is shorthand for "the limit of the
sequence of numbers
,
9
10
,
9 9
10 100
....",
9 9 9
10 100 1000
Question: 5
What can the maximum number of digits be in the
repeating block of digits in the decimal expansion
of ?
1
17
Perform the division to check your answer.
Solution:
1
0.0588235294117647
17
There are 16 digits in the repeating block of the
decimal expansion of .
1
17

Division Check:
1
0.0588235294117647
17
Question: 6
Look at several examples of rational numbers in the
from where p and q are integers with no
p
q
q 0

common factors other than 1 and having terminating
decimal representations (expansions).
Can you guess what property q must satisfy?
Solution:
We observe that when q is 2, 4, 5, 8, 10… then the
decimal expansion is terminating.
For example:
, the denominator
0.5
1
2
1
q 2
the denominator
0.875,
7
8
3
q 2
, the denominator
0.8
4
5
1
q 5
We can observe that terminating decimal may be
obtained in the situation where prime factorisation
of the denominator of the given rational number has
the power of 2 only or 5 only or both.
Question: 7
Write three numbers whose decimal expansions are
non-terminating non-recurring.
Solution:
Three numbers whose decimal expansions are non-
terminating non-recurring are:
√2, √3 and √5 or

0.303003000300003...,0.505005000500005...
and0.7207200720007200007200000…
Question: 8
Find three different irrational numbers between the
rational numbers and .
5
7
9
11
Solution:
0 4
5
7
.71
0
1
8
9
1
.81
Three different irrational numbers between the
rational numbers and are:
5
7
9
11
0.72072007200072000072…
0.74074007400074000074…
0.75075007500075000075…
Question: 9
Classify the following numbers as rational or
irrational:
(i) √23
(ii) √225

(iii) 0.3796
(iv) 7.478478…
(v) 1.101001000100001…
Solution:
(i)
..23 4.79583152331.
The number is non-terminating non-recurring. It is
an irrational number.
(ii)
15
1
225 15
The number can be represented in the form ,
p
q
P and q are integers and q ≠ 0. It is a rational
number.
(iii) 0.3796
The decimal is terminating. It is a rational number.
(iv) 7.478478…
This number is non-terminating but recurring. It is a
rational number.
(v) 1.101001000100001…

The number is non-terminating and non-repeating. It
is an irrational number.
EXERCISE: 1.4
Question: 1
Visualise 3.765 on the number line using successive
magnification.
Solution
Question: 2
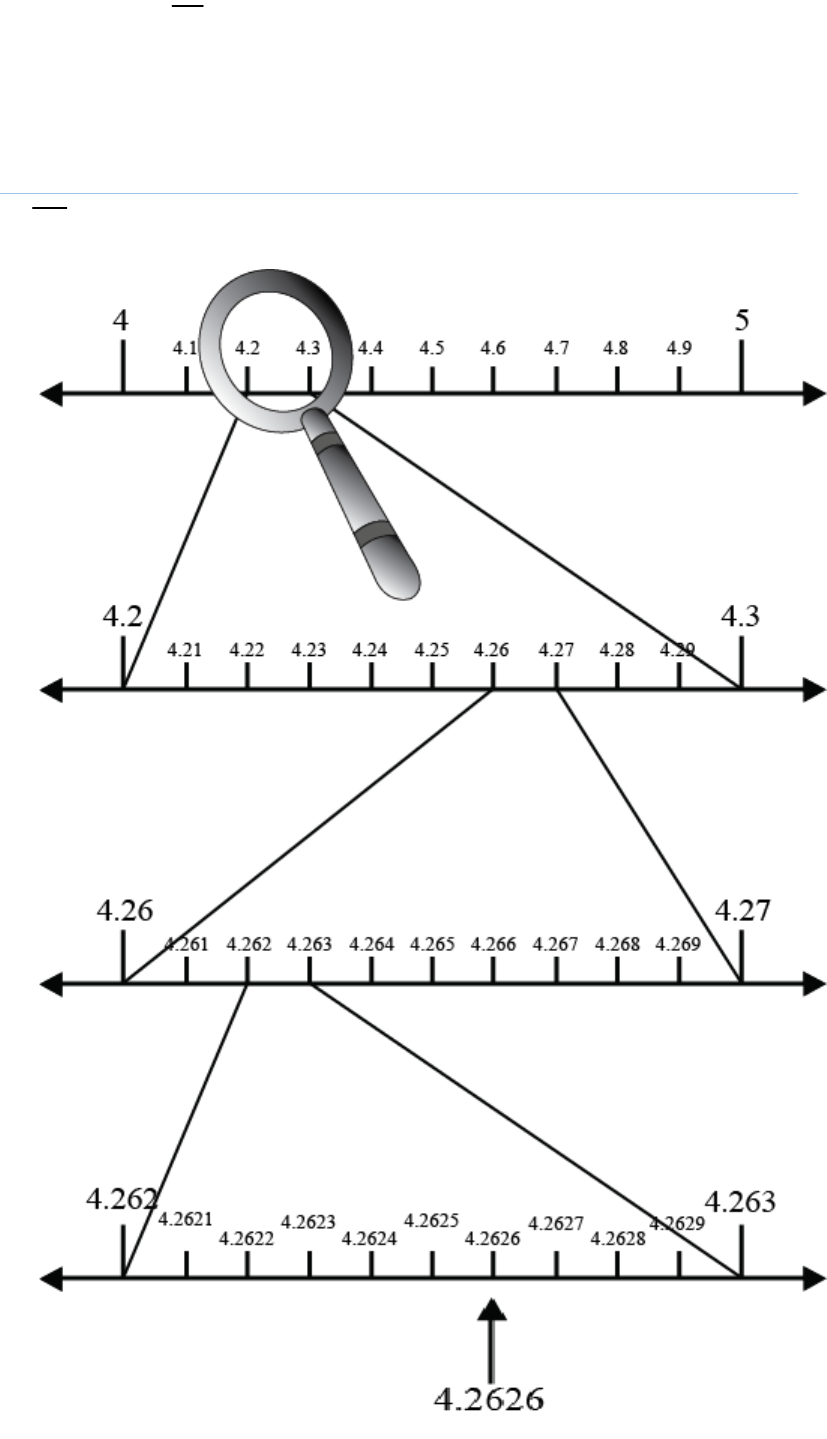
Visualise on the number line, up to 4 decimal
4.26
places.
Solution:
4.26 4.2626...

EXERCISE: 1.5
Question: 1
Classify the following numbers as rational or
irrational:
(i)
2 5
(ii)
3 23 23
(iii)
2 7
7 7
(iv)
1
2
(v)
2π
Solution:
(i)
2 5
The sum of a rational number and an irrational
number is always irrational. Here, 2 is rational and
is irrational. If we put the value of in the
5
5
expression, we find 2−2.236079 or -0.236079.
As, the decimal expansion of this expression is non-
recurring. Therefore, it is an irrational number.

(ii)
3 23 23 = 3 23 23 = 3
3 is a natural number and can be written as
3
1
Therefore, it is a rational number.
(iii)
2 7 2
7
7 7
The number is in the form of ,
p
q
where p and q are integers and q ≠ 0.
Therefore, it is a rational number.
(iv)
1
2
The quotient of a nonzero rational number and an
irrational number is always irrational. Therefore, it is
an irrational number.
(v)
2π
The product of a nonzero rational number and an
irrational number is always irrational.
is an irrational number. Therefore, is an
π
2π
irrational number.

Question: 2
Simplify each of the following expressions:
(i)
3 23 2
(ii)
3 33 3
(iii)
5 2
2
(iv)
5 2 5 2
Solution:
(i)
3 23 2
2 3 23 2 2
2 3 66 3 2
3 2 6 6 2 3
(ii)
3 33 3
[Using the formula, ]
2 2
a b a b = a b
3
2
2
3

9 3 6
(iii) [Using the formula,
5 2
2
2
a + b
]
2 2
a b 2ab
2 2
= 5 2 2 5 2
= 5 + 2 2 5 2 2
7 2 10
(iv) [Using the formula,
5 2 5 2
]
2 2
a b a b = a b
Question: 3
Recall, π is defined as the ratio of the circumference
(say c) of a circle to its diameter (say d).
That is, .
c
π
d
This seems to contradict the fact that is irrational.
How will you resolve this contradiction?
Solution:

There is no contradiction. There do not exist two
integers a and b such that It is a proven fact
a c
b d
that is a constant and turns out to be a non -
c
d
terminating and non - repeating decimal. The value
of is approximately equal to or 3.142857…
π
22
7
Question: 4
Represent on the number line.
9.3
Solution:
Let’s draw a line and mark a point say A on it. Mark
a point on the number such that units.
AB 9.3
Let’s mark a point C such that BC is 1 unit as
shown. Mark the point on the midpoint of AC as D.
Let’s draw a circle with centre D and radius DC.

Let’s draw a line perpendicular to AC passing
through B and intersecting the semi-circle at E.
As units and unit,
9.3AB
BC 1
units
9.3 1AC
units
9.3+1
DA DC
2
units
9.3 1
DE
2
+
As DA DC DE
Now,
9.3 1 9.3 1
DB AB DA 9.3
2 2
+
Using Pythagoras theorem in ∆DBE, we have
2 2 2
DE DB BE
2 2 2
BE DE DB

2 2
2
9.3 1 9.3 1
BE
2 2
2 2
9.3 2(9.3) 1 9.3 2(9.3) 1
BE
4
+ +
4(9.3)
9.3
4
2 2 2
BE DE DB
2 2
2
9.3 1 9.3 1
BE
2 2
2 2
9.3 2(9.3) 1 9.3 2(9.3) 1
BE
4
+ +
4(9.3)
9.3
4
With B as centre and radius BE; draw an arc
intersecting the number line at F.
So, BE = BF represents
9.3
Question: 5

Rationalise the denominators of the following:
(i)
1
7
(ii)
1
7 6
(iii)
1
5 2
(iv)
1
7 2
Solution:
(i)
1 1 7 7
7
7 1 7 7
×
×
(ii)
1 1( 7 6)
7 6 ( 7 6)( 7 6)
+ +
+
2 2
7 6 7 6
7 6
1
( 7) ( 6)
(iii)
1 1( 5 2)
5 2 ( 5 2)( 5 2)
+ +
2 2
5 2 1( 5 2)
3
( 5) ( 2)

(iv)
1 1( 7 2)
7 2 ( 7 2)( 7 2)
+
+
+
2 2
7 2 7 2 7 2
7 4 3
( 7) (2)
EXERCISE: 1.6
Question: 1
Find:
(i)
1
2
64
(ii)
1
5
32
(iii)
1
3
125
Solution:
(i)
1 1 1
2 2 2
6
6 3
64 = (2 ) = 2 = 2 = 8
(ii)
1 1 1
5 5 5
5
5
32 = (2 ) = (2) = 2
(iii)
1 1
3 3
3
(125) = (5 ) = 5
Question: 2
Find:
(i)
3
2
9

(ii)
2
5
32
(iii)
3
4
16
(vi)
1
-
3
125
Solution:
(i)
2
2 3
3 3 3
2 2 2
9 (3 ) 3 3 27
(ii)
5
2
2 2 2
5 5 5
5
32 (2 ) (2) = 2 = 4
(iii)
4 3
3 3
4 4
(16) (2 ) 2 8
(iv)
-1
3
1 1
3 3
1 1 1
(125)
5
3
(125) (5 )
Question: 3
Simplify:
(i)
2 1
3 5
2 .2
(ii)
7
3
1
3

(iii)
1
2
1
4
11
11
(iv)
1 1
2 2
7 .8
Solution:
(i)
2 1 2 1 10 3 13
3 5 3 5 15 15
2 .2 2 2 2
(ii)
7
21
3 3 7 21
1 1 1
= = 3
3 3 3
(iii)
1
1 1 2 1 1
2
2 4 4 4
1
4
11
=11 =11 =11
11
(iv)
1 1 1 1
2
2 2 2 2
7 .8 = (7 2 2) = 2 14