
Lesson: Polynomials
EXERCISE: 2.1
Question: 1
Which one of the following is a polynomial?
(a)
2
2
2
2
x
x
(b)
2 1x
(c)
3
2
2
3
x
x
x
(d)
1
1
x
x
Solution:
(a)
2 2
2
2
2 1
2 2 2
x x
x
x
The exponent of the variable after simplification is
not a whole number.
So, it is not a polynomial.
(b)
1 1 1
2 2 2
2 1 (2 ) 1 2 1 x x x
The exponent of the variable after simplification is
not a whole number.
So, it is not a polynomial.
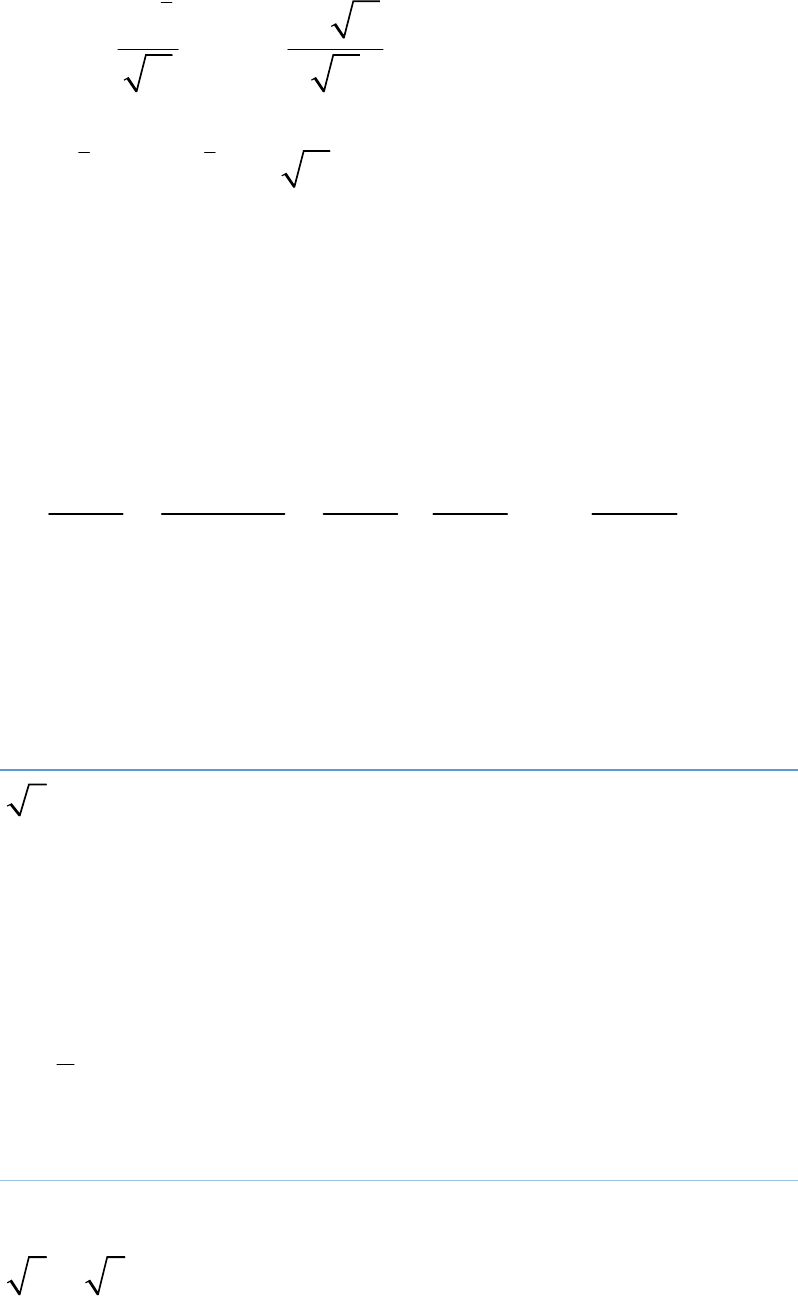
(c)
3
2
2 2 2
3 3
3
x x x
x x x x
x x
[ = ]
3 1
2 2
1
x x x x x
The exponent of the variable after simplification is a
whole number.
So it is a polynomial.
Hence, option (c) is correct.
(d)
1 1 2 1 2
2
1
( 1)
1 1 1 1
x x x
x
x x x x
The exponent of the variable after simplification is
not a whole number. So, it is not a polynomial.
Question: 2
is a polynomial of degree:
2
(a) 2
(b) 0
(c) 1
(d)
1
2
Solution:
b
0
2 2. x
The exponent of the variable after simplification is 0.
So, it is a polynomial of degree 0. Hence, the option
(b) is correct.

Question: 3
Degree of the polynomial
is:
4 3 5
4 0 0 5 7 x x x x
(a) 4
(b) 5
(c) 3
(d) 7
Solution:
a
The highest exponent of the variable is 4, so it is a
polynomial of degree 4. Hence, the option (a) is
correct.
Question: 4
Degree of the zero polynomial is:
(a) 0
(b) 1
(c) Any natural number
(d) Not defined
Solution:
d
The highest exponent of the variable can be any
whole number in zero polynomial, so its degree can’t
be defined. Hence, the option (d) is correct
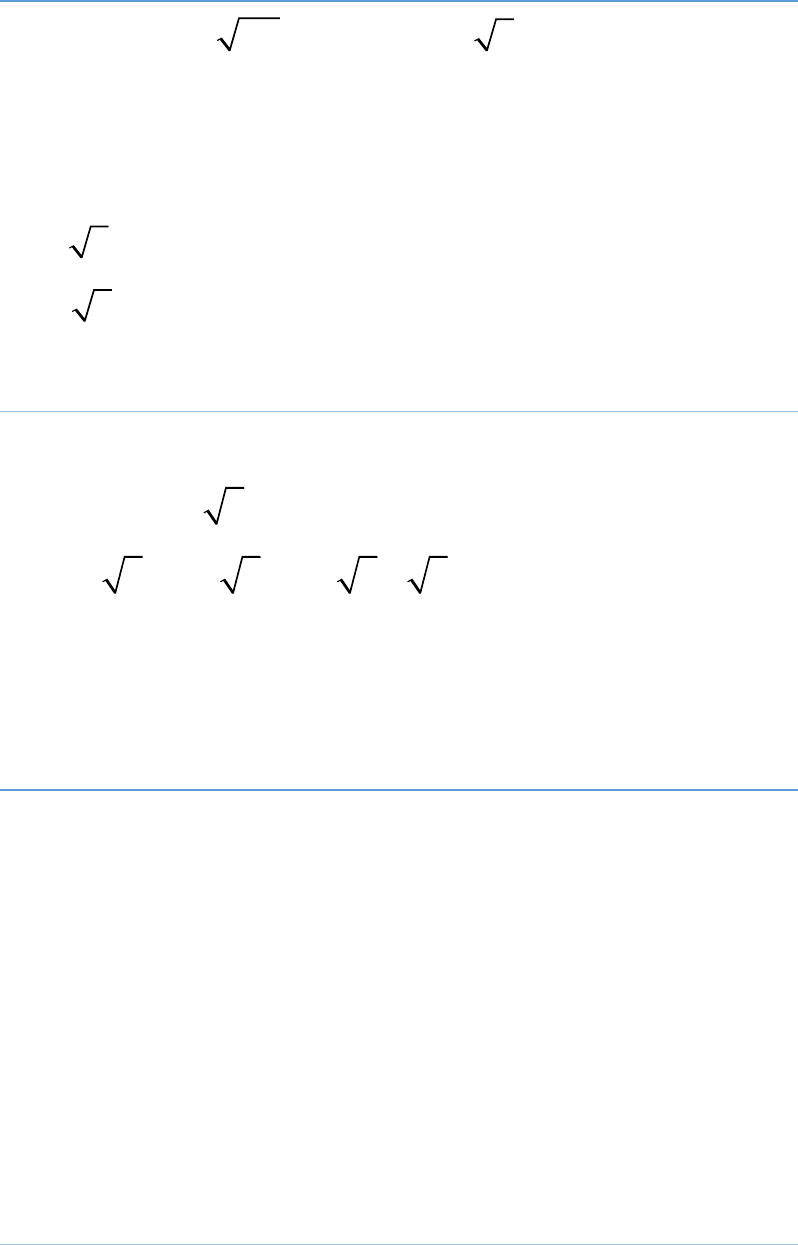
Question: 5
If then is equal to:
2
2 2 1, p x x x
2 2p
(a) 0
(b) 1
(c)
4 2
(d)
8 2 1
Solution:
b
2
( ) 2 2 1 p x x x
So,
2
(2 2) (2 2) 2 2(2 2) 1 p
8 8 1 1
Hence, option (b) is correct
Question: 6
The value of the polynomial when
2
5 4 3, x x
x = − 1is:
(a) −6
(b) 6
(c) 2
(d) −2
Solution:
a
Given polynomial:
2
( ) 5 4 3 p x x x
So,
2
( 1) 5( 1) 4( 1) 3 p
5 4 3 6

Hence, option (b) is correct
Question: 7
If then is equal to:
3,p x x
p x p x
(a) 3
(b) 2x
(c)
0
(d) 6
Solution:
d
Given polynomial:
( ) 3 p x x
So,
( ) ( ) 3 ( ) 3 p x p x x x
6 6 x x
Hence, option (d) is correct
Question: 8
Zero of the zero polynomial is:
(a) 0
(b) 1
(c) Any real number
(d) Not defined
Solution:
c
Every real number is a zero of a zero polynomial.
Hence, option (c) is correct.

Question: 9
Zero of the polynomial is:
2 5p x x
(a)
2
5
(b)
5
2
(c)
2
5
(d)
5
2
Solution:
b
Given polynomial:
( ) 2 5 p x x
For zeroes,
( ) 0p x
2 5 0 x
5
2
x
Hence, option (b) is correct
Question: 10
One of the zeroes of the polynomial
is:
2
( ) 2 7 4 p x x x
(a)
2
(b)
1
2
(c)
1
2
(d) −2

Solution:
b
Given polynomial:
2
( ) 2 7 4 p x x x
For zeroes, p(x) = 0
2
2 7 4 0 x x
2
2
8 4 0 x x x
2 ( 4) 1( 4) 0 x x x
( )( )4 2 1 0 x x
or 24 0 1 0 x x
or
1
4
2
x x
Hence, option (b) is correct
Question: 11
If is divided by x + 1, remainder is:
51
51x
(a) 0
(b) 1
(c) 49
(d) 50
Solution:
d
Given polynomial:
51
( ) 51 p x x
Using remainder theorem; if is
51
( ) 51 p x x
divided by x + 1, remainder is given by p(−1).

51
( 1) ( 1) 51 1 51 50 p
Hence, option (b) is correct
Question: 12
If x + 1 is a factor of the polynomial , then
2
2 x kx
the value of k is:
(a) −3
(b)
4
(c)
2
(d) −2
Solution:
c
Given polynomial:
2
( ) 2 p x x kx
According to factor theorem, if
2
( ) 2 p x x kx
is divided by x + 1, then p(−1)=0.
( 1) 0 p
2
2( 1) ( 1) 0 k
2 0 k
k 2
Hence, option (c) is correct

Question: 13
x + 1 is a factor of the polynomial.
(a)
3 2
1 x x x
(b)
3 2
1 x x x
(c)
4 3 2
1 x x x
(d)
4 3 2
3 3 1 x x x x
Solution:
b
According to Factor Theorem, if the polynomial is
divided by x + 1, the remainder is 0.
In case (a),
+ -
3 2
( ) 1 p x x x x
3 2
( 1) ( 1) ( 1) ( 1) 1 p
1 1 1 1 2 0
So, x + 1 is not a factor of this polynomial.
In case (b),
+
3 2
( ) 1 p x x x x
3 2
( 1) ( 1) ( 1) 1 1 p
1 1 1 1 0
So, x + 1 is not a factor of this polynomial.
In case (c),
+
4 3 2
( ) 1 p x x x x
4 3 2
( 1) ( 1) ( 1) ( 1) 1 p

1 1 1 1 2 0
So, x + 1 is not a factor of this polynomial.
In case (d),
+3
4 3 2
( ) 3 1 p x x x x x
4 3 2
( 1) ( 1) 3( 1) 3( 1) 1 1 p
1 3 3 1 1 1 0
So, x + 1 is not a factor of this polynomial.
Hence, option (b) is correct.
Question: 14
One of the factors of is:
2
2
25 1 1 5 x x
(a)
5 x
(b)
5 x
(c)
5 1x
(d) 10x
Solution:
d
Given polynomial: .
2 2
( ) (25 1) (1 5 ) p x x x
2 2
( ) (25 1) (1 25 10 ) p x x x x
2
50 10 x x
10 (5 1) x x
and 5x + 1 are the factors of the given
10 x
polynomial.
Hence, option (d) is correct.
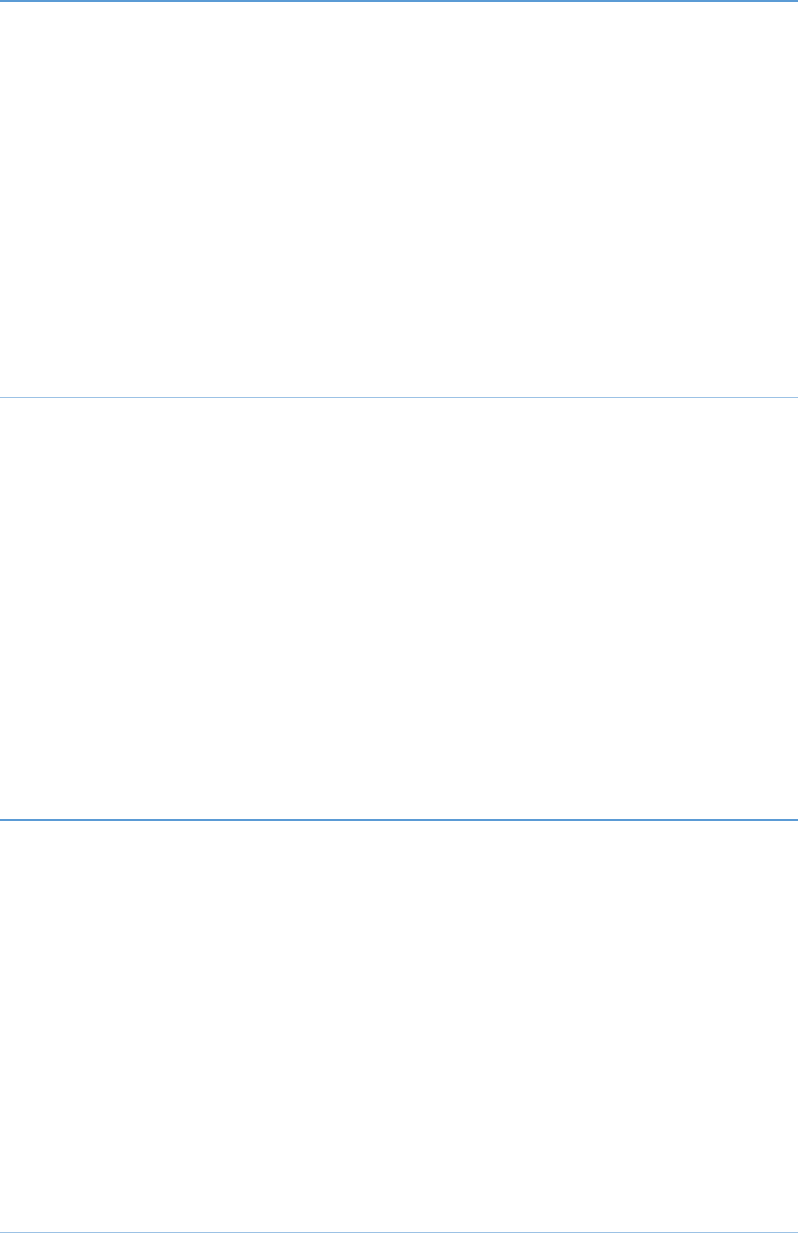
Question: 15
The value of is:
2 2
249 248
(a)
2
1
(b) 477
(c) 487
(d) 497
Solution:
d
2 2
249 248
2 2
(249 248) (249 248) [ ( )( )] a b a b a b
1 497
497
Hence, option (d) is correct.
Question: 16
The factorisation of
is :
2
4 8 3 x x
(a)
1 3x x
(b)
2 1 2 3x x
(c)
2 2 2 5x x
(d)
2 1 2 3x x
Solution:
b
2
4 8 3 x x
2
4 6 2 3 x x x
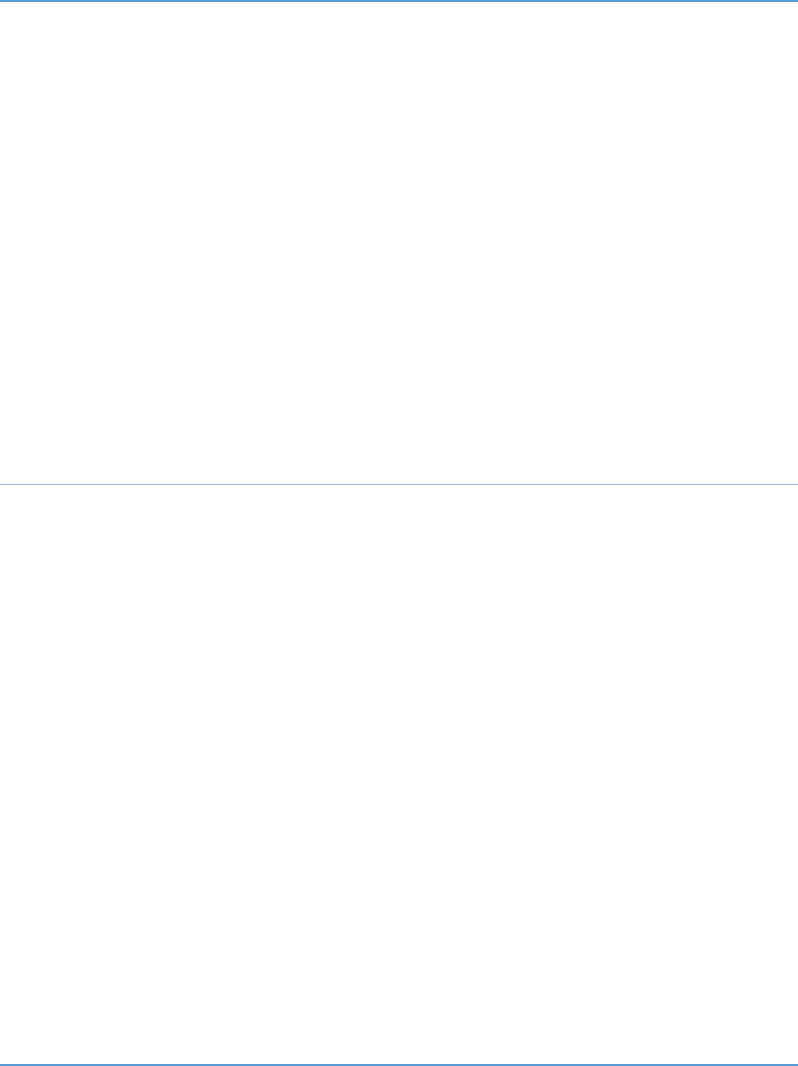
2 (2 3) 1(2 3) x x x
(2 1)(2 3) x x
Hence, option (b) is correct.
Question: 17
Which of the following is a factor of
?
( )
3 3 3
( ) x y x y
(a)
2 2
2 x y xy
(b)
2 2
x y xy
(c)
2
xy
(d)
3xy
Solution:
d
( )
3 3 3
( ) x y x y
3 3 2 2 3 3
( 3 3 ) ( ) x y x y xy x y
2 2
3 3 x y xy
3 ( ) xy x y
and (x + y) are the factors of the given
3 xy
polynomial
Hence, option (d) is correct.
Question: 18
The coefficient of x in the expansion of
is:
3
3x
(a)
1
(b) 9

(c)
18
(d)
27
Solution:
d
Given polynomial:
( )
3
3x
3 3 2 2
3 3 3 3 3 x x x
3 2
27 9 27 x x x
The coefficient of x in the expansion is 27:
( )
3
3x
Hence, the option (d) is correct
Question: 19
If (where x, y ≠ 0), the value of
1
x y
y x
3 3
x y
is:
(a)
1
(b) −1
(c) 0
(d)
1
2
Solution:
c
1
x y
y x
2 2
1
x y
xy

2 2
x y xy
2 2
0 x y xy
Now,
3 3
x y
2 2
( )( ) x y x y xy
( )(0) x y
0
Hence, the option (c) is correct
Question: 20
If then the value of
2
1 1
49 7 7 ,
2 2
x b x x
b is:
(a) 0
(b)
1
2
(c)
1
4
(d)
1
2
Solution:
c
2
1 1
49 (7 )(7 )
2 2
x b x x
2
2 2
1
49 (7 )
2
x b x

2 2
1
49 49
4
x b x
1
4
b
Hence, the option (c) is correct.
Question: 21
If a + b + c = 0, then is equal to:
3 3 3
a b c
(a) 0
(b) abc
(c) 3abc
(d) 2abc
Solution:
c
We know that:
3 3 3
3 ( ) a b c abc a b c
2 2 2
( ) a b c ab bc ca
If a + b + c = 0, then we have
3 3 3 2 2 2
3 (0)( ) a b c abc a b c ab bc ca
3 3 3
3 0 a b c abc
3 3 3
3 a b c abc
Hence, the option (c) is correct.

EXERCISE: 2.2
Question: 1
Which of the following expressions are polynomials?
Justify your answer:
(i) 8
(ii)
2
3 2x x
(iii)
1 5x
(iv)
2
1
5 7
5
x
x
(v)
2 4x x
x
(vi)
1
1x
(vii)
3 2
1 2
4 7
7
3
a a a
(viii)
1
2x
Solution:
i
0 0
8 8 ] 1[ x a
The exponent of the variable after simplification is a
whole number. So it is a polynomial.
(ii)
1 1 1
2
2 2
2 2 2
3 2 (3 ) 2 3 2
x x x x x x

3 2 ( 3 2) x x x
The exponent of the variable after simplification is a
whole number. So it is a polynomial.
(iii)
1
2
1 1
2 2
1 5 1 (5 ) 1 5 x x x
The exponent of the variable after simplification is
not a whole number. Therefore, it is not a
polynomial.
(iv)
2
2
1 1 1
5 7 5 7 [ ]
5 5
x x x a
x a
n
n
The exponent of the variable after simplification is a
whole number. Therefore, it is a polynomial.
(v)
2
1
2 4
6 8
6 8
x x
x x
x x
x x
The exponent of the variable after simplification is
not a whole number. Therefore, it is not a
polynomial.
(vi)
1
1
( 1)
1
x
x

The exponent of the variable after simplification is
not a whole number. Therefore, it is not a
polynomial.
(vii)
3 2
1 2
4 7
7
3
a a a
The exponent of the variable after simplification is a
whole number. Therefore, it is a polynomial.
(viii)
1
1 1
2 2
x
x
The exponent of the variable after simplification is
not a whole number.
Therefore, it is not a polynomial.
Question: 2
Write whether the following statements are True or
False. Justify your answer.
(i) A binomial can have at most two terms.
(ii) Every polynomial is a binomial.
(iii) A binomial may have degree 5.
(iv) Zero of a polynomial is always 0.
(v) A polynomial cannot have more than one zero.
(vi) The degree of the sum of two polynomials each
of degree 5 is always 5.
Solution:

(i) False, because the binomial has two terms only.
(ii) False, is a polynomial but not a
3
1 x x
binomial.
(iii) True, because a binomial is a polynomial whose
degree is a whole number 1.
So, the degree can be 5 also.
(iv) False, because zero of a polynomial can be any
real number.
(v) False, a polynomial can have any number of
zeroes. It depends upon the degree of the
polynomial.
(vi) False, and are two
5
1x
5
2 3 x x
polynomials of degree 5 but the degree of the
sum of the two polynomials is 1.
EXERCISE: 2.3
Question: 1
Classify the following polynomials as polynomials in
one variable, two variables etc.

(i)
2
1 x x
(ii)
3
5y y
(iii)
xy yz zx
(iv)
2 2
2 1 x xy y
Solution:
i
2
1 x x
It is a polynomial in one variable
(x is the only variable).
ii
3
5y y
It is a polynomial in one variable
(y is the only variable).
iii xy yz zx
It is a polynomial in three variables
(x, y and z are the variables).
iv
2 2
2 1 x xy y
It is a polynomial in two variables
(x and y are the variables).
Question: 2
Determine the degree of each of the following
polynomials:
(i)
2 1x

(ii) −10
(iii)
3 5
9 3 x x x
(iv)
3 4
1y y
Solution:
i 2 1x
The greatest exponent of the variable is 1. So, the
degree is 1.
ii
0
10 10 x
The greatest exponent of the variable is 0. So, the
degree is 0.
iii
3 5
9 3 x x x
The greatest exponent of the variable is 5. So, the
degree is 5.
iv
3 4 3 7
1 y y y y
The greatest exponent of the variable is 7. So, the
degree is 7.
Question: 3
For the polynomial:

Write
3
2 6
2 1 7
,
5 2
x x
x x
(i) the degree of the polynomial.
(ii) the coefficient of x
3
.
(iii) the coefficient of x
6
.
(iv) the constant term.
Solution:
(i)
3
2 6
2 1 7
5 2
x x
x x
The greatest exponent of the variable is 6. So, the
degree is 6.
(ii)
3
2 6
2 1 7
5 2
x x
x x
3 2 6
1 2 1 7
5 5 5 2
x x x x
The coefficient of is .
3
x
1
5
(iii)
3
2 6
2 1 7
5 2
x x
x x
3
2 6
2 1 7
1
5 2
x x
x x
The coefficient of is
6
x
.1

(iv)
3
2 6 3 2 6
2 1 7 1 2 1 7
5 2 5 5 5 2
x x
x x x x x x
The constant term is .
1
5
Question: 4
Write the coefficient of in each of the following:
2
x
(i)
2
π
1
6
x x
(ii)
3 5x
(iii)
x 1 3 4x
(iv)
2
2 5 2 3 1 x x x
Solution:
(i)
2 2
π π
1 1 1
6 6
x x x x
The coefficient of is 1.
2
x
(ii)
2
3 5 0 3 5 x x x
The coefficient of is 0.
2
x
(iii)
2
1 3 4 3 7 4 x x x x

The coefficient of is 3.
2
x
(iv)
2
2 5 2 3 1 x x x
3 2 2
4 6 2 10 15 5 x x x x x
3 2
4 16 17 5 x x x
The coefficient of is −16.
2
x
Question: 5
Classify the following as constant, linear, quadratic
and cubic polynomials:
(i)
2 3
2 x x
(ii)
3
3x
(iii)
5 7t
(iv)
2
4 5 y
(v)
3
(vi)
2 x
(vii)
3
y y
(viii)
2
1 x x
(ix)
2
t
(x)
2 1x
Solution:
(i)
2 3
2 x x
Here, the given polynomial has degree 3.

Therefore, this polynomial is a cubic polynomial.
(ii)
3
3x
Here, the given polynomial has degree 3.
Therefore, this polynomial is a cubic polynomial.
(iii)
5 7t
Here, the given polynomial has degree 1.
Therefore, this polynomial is a linear polynomial.
(iv)
2
4 5 y
Here, the given polynomial has degree 2.
Therefore, this polynomial is a quadratic
polynomial
(v)
0
3 3 x
Here the given polynomial has degree 0.
Therefore, this polynomial is a constant
polynomial
(vi)
2 x
Here, the given polynomial has degree 1.
Therefore, this polynomial is a linear polynomial.

(vii)
3
y y
Here, the given polynomial has degree 3.
Therefore, this polynomial is a cubic polynomial.
(viii)
2
1 x x
Here, the given polynomial has degree 2.
Therefore, this is a quadratic polynomial.
(ix)
2
t
Here, the given polynomial has degree
2.Therefore, this is a quadratic polynomial.
(x)
2 1x
This polynomial has degree 1. Therefore, it is a
linear polynomial.
Question: 6
Give an example of a polynomial, which is:
(i) Monomial of degree 1
(ii) Binomial of degree 20
(iii) Trinomial of degree 2
Solution:
(i) Monomials have only one term.
Therefore, 10x is a monomial of degree 1.

(ii) Binomials have only two terms.
Therefore, is a binomial of degree 20.
20
16x 1
(iii) Trinomials have only three terms.
Therefore, is a trinomial of degree
2
8x – x 1
2.
Question: 7
Find the value of the polynomial ,
3 2
3 4 7 5 x x x
when x = 3 and also when
x = –3.
Solution:
Given polynomial,
.
3 2
3 4 7 5 x x x
When x = 3
3 2
3 3 4 3 7 3 5
81 36 21 5
102 41
61
When x = –3
3 2
3 3 4 3 7 3 5

81 36 21 5
143
Question: 8
If evaluate:
2
4 3, p x x x
1
2 1
2
p p p
Solution:
2
4 3, p x x x
1
2 1
2
p p p
2
2 2
1 1
2 4 2 3 1 4 1 3 4 3
2 2
1
4 8 3 1 4 3 2 3
4
1 8 12
1 8
4
5
9
4
36 5 31
4 4
Question: 9
Find for the following polynomials:
0 , 1 , 2p p p
(i)
2
10 4 3 p x x x
(ii)
2 2 p y y y

Solution:
i
2
10 4 3 p x x x
2
0 10 0 4 0 3 p
3
2
1 10 1 4 1 3 p
10 7 3
2
1 10 1 4 1 3 p
10 7 3
2
2 10 2 4 2 3 p
20 16 3 39
(ii)
2 y 2p y y
0 0 2 0 2 p
4
1 1 2 1 2 p
3 1
3
2 2 2 2 2 p
0 4
0
Question: 10
Verify whether the following are True or False:
(i) –3 is a zero of x – 3

(ii)
is zero of
1
3
3 1x
(iii) is zero of
4
5
4 5y
(iv) 0 and 2 are the zeroes of – 2t
2
t
(v) –3 is a zero of y
2
+ y – 6
Solution:
(i) False,
( ) 3 p x x
( 3) 3 3 6¹0 p
is a not a zero of 3 3 x
(ii) True
( ) 3 1 p x x
1
1
( ) 3 1 1 1 0
3
3
p
1
is a zero of 3 1
3
x
(iii) False
( ) 4 5 p x y
4
4
( ) 4 5 4 4 8 0
5
5
p

is a not a zero of
4
4 5
5
y
(iv) True
2
( ) 2 p x t t
2
(0) 0 2(0) 0 p
0 is a zero of
2
2 t t
And
2
( ) 2 p x t t
2
(2) 2 2(2) 4 4 0 p
2 is a zero of
2
2 t t
(v) True
2
( ) 6 p x y y
2
( 3) ( 3) ( 3) 6 9 9 0 p
is a zero of
3
2
6 y y
Question: 11
Find the zeroes of the polynomial in each of the
following:
(i)
4 p x x
(ii)
3 6 g x x
(iii)
2 7 q x x
(iv)
2h y y
Solution:

i 4p x x
4 0 x
4 x
ii 3– 6g x x
3 6 0 x
6 3 x
3 1
6 2
x
(iii) q(x) = 2x –7
2 7 0 x
7
2
x
(iv) h(y) = 2y
2 0y
0
0
2
y
Question: 12
Find the zeroes of the polynomial:
2 2
2 2 p x x x
Solution:
2 2
2 2 p x x x
2 2
2 2 0 x x

2 2 2 2
2 2. .2 2 2. .2 0 x x x x
2 2
4 4 4 4 0 x x x x
8 0 x
0 x
Question: 13
By actual division, find the quotient and the
remainder when the first polynomial is divided by
the second polynomial:
4
1; – 1x x
Solution:
Question: 14
By remainder theorem find the remainder, when p(x)
is divided by g(x), where
(i)
3 2
2 4 1, 1p x x x x g x x

(ii)
3 2
3 4 50 3, p x x x x g x x
(iii)
3 2
4 12 14 3, 2 1 p x x x x g x x
(iv)
3 2
3
6 2 4, 1
2
p x x x x g x x
Solution:
(i)
3 2
2 4 1 p x x x x
1 1 2 4 1 p
1 0 p
The remainder is 0.
(ii)
3 3
3 4 50 p x x x x
3 27 27 12 50 p
62
The remainder is 62.
(iii)
3 2
4 12 14 3 p x x x x
3 2
1 1 1 1
4 12 14 3
2 2 2 2
p
1
3 7 3
2
1 6 14 6
2
3
2

(iv)
3 2
6 2 4 p x x x x
3
1 0
2
g x x
2
3
x
3 2
2 2 2 2
6 2 4
3 3 3 3
p
8 24 4
4
27 9 3
8 72 36 108
27
44 180
27
136
27
Question: 15
Check whether p(x) is a multiple of g(x) or not:
(i)
3 2
5 4 3, 2 p x x x x g x x
(ii)
3 2
2 11 4 5, 2 1 p x x x x g x x
Solution:
(i)
3 2
5 4 3, p x x x x
2 g x x
3
2 2 5 4 4 2 3 p
8 20 8 3

7
0
is not a multiple of g(x)
p x
(ii)
3 2
2 11 4 5 p x x x x
2 1 g x x
3 2
1 1 1 1
2 11 4 5
2 2 2 2
p
1 11 4
5
4 4 2
1 11 8 20
4
16
4
4
0
is not a multiple of g(x)
p x
Question: 16
Show that:
(i) x + 3 is a factor of .
2 3
69 11 x x x
(ii) 2x – 3 is a factor of .
3 2
2 9 12 x x x
Solution:

(i) Let
3 2
( ) 11 69 p x x x x
3 g x x
3 2
3 3 3 11 3 69 p
27 9 33 69
0
is a factor of p(x)
3 x
(ii) Let
3 2
2 9 12 p x x x x
2 3 g x x
3 2
3 3 3 3
2 9 12
2 2 2 2
p
27 9 3
2 9 12
8 4 2
27 81 3
12
4 4 2
27 81 6 48
4
81 81
4
0
is a factor of p(x)
2 3 x
Question: 17
Determine which of the following polynomials has x
– 2 a factor:

(i)
2
3x 6x – 24
(ii)
2
4x x – 2
Solution:
(i)Let
2
3 6 24 p x x x
2
2 3 2 6 2 24 p
12 12 24
0
is a factor of p(x)
2 x
(ii)
2
4 2 p x x x
2
2 4 2 2 2 p
16
is not a factor of p(x)
2 x
Question: 18
Show that is a factor of and also of
1p
10
1p
.
11
1p
Solution:
(i) Let
10
1 g x p
10
(1) 1 1 g
0
is a factor of g(x)
1 x

(ii) Let
11
1 g x p
11
(1) 1 1 g
1 1
0
is a factor of g(x)
1x
Question: 19
For what value of m is divisible by
3 2
2 16 x mx
?
2x
Solution:
Let
3 2
2 16 p x x mx
2 g x x
is divisible by
p x
g x
2 0 p
3 2
2 2 2 16 0 m
8 8 16 0 m
8 8 m
1 m
Question: 20
If is a factor of , find .
2x a
5 2 3
4 2 2 3 x a x x a
a
Solution:
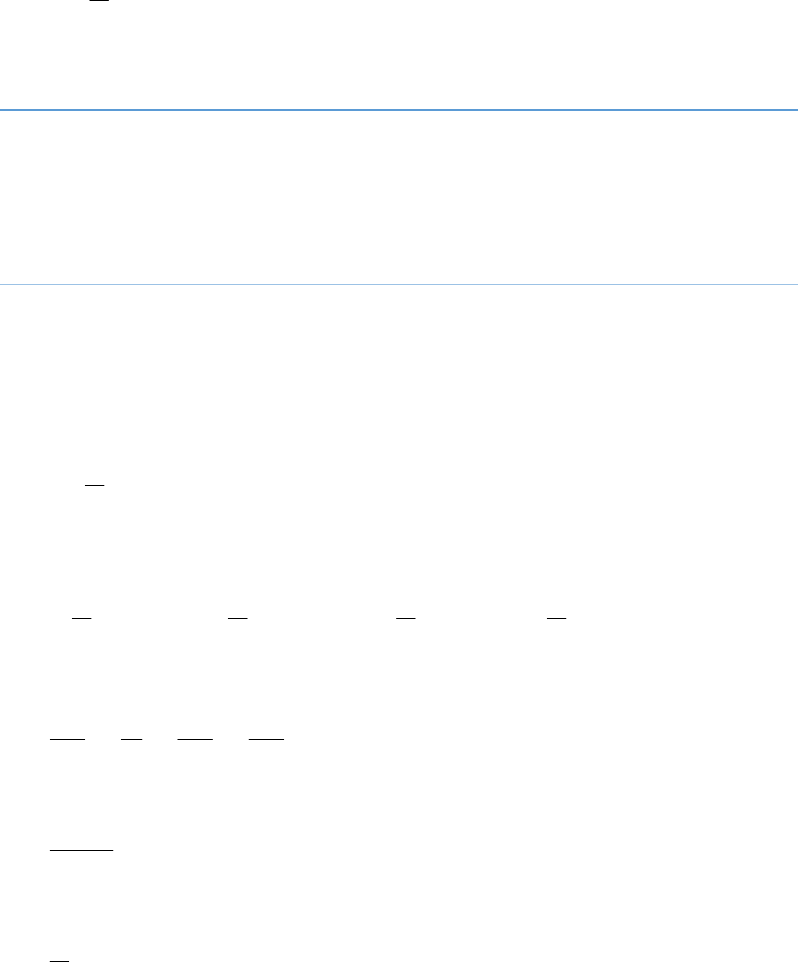
Let
5 2 3
4 2 2 3 p x x a x x a
is a factor of p(x)
2x a
2 0 p a
5 3
2
2 4 2 2 2 2 3 0 a a a a a
5 5
32 32 4 2 3 0 a a a a
2 3 a
3
2
a
Question: 21
Find the value of so that be a factor of
m
2 1x
4 3 2
8 4 16 10 x x x x m
Solution:
Let
4 3 2
8 4 16 10 p x x x x x m
is a factor of p(x)
2 1x
1
0
2
p
4 3 2
1 1 1 1
8 4 16 10 0
2 2 2 2
m
8 4 16 10
0
16 8 4 2
m
1 1
4 5 0
2
m
2
1 0
2
m
2 m

Question: 22
If is a factor of , then find
1x
3 2
2 4 9 ax x x a
the value of .
a
Solution:
Let
3 2
2 4 9 ax xp x ax
is a factor of so,
1x
p x
1 0 p
3 2
( 1) ( 1) 2( 1) 4 9 0 a a
1 2 4 9 0 a a
3 6 0 a
6
2
3
a
Question: 23
Factorise:
(i)
2
9 18 x x
(ii)
2
6 7 3 x x
(iii)
2
2 7 15 x x
(iv)
2
84 2 2 r r
Solution:
(i) Given that
2
( ) 9 18 p x x x
2
( 6 3 18) x x x
{ ( 6) 3( 6)} x x x
( 6)( 3) x x

(ii) Given that
2
( ) = 6 7 3 p x x x
2
= 6 9 2 3 x x x
3 (2 3) 1(2 3) x x x
(2 3)(3 1) x x
(iii) Given that
2
( ) 2 7 15 p x x x
2
= 2 10 3 15 x x x
2 ( 5) 3( 5) x x x
( 5)(2 3) x x
(iv) Given that
2
( ) 84 2 2 p x r r
2
2( 42) r r
2
2( 7 6 42) r r r
2{ ( 7) 6( 7)} r r r
2( 7)( 6) r r
2(7 )(6 ) [( 6) (6 )] r r r r
Question: 24
Factorise:
(i)
3 2
2 3 17 30 x x x
(ii)
3 2
6 11 6 x x x
(iii)
3 2
4 4 x x x

(iv)
3 2
3 3 1 x x x
Solution:
(i) Given that
3 2
( ) 2 3 17 30 p x x x x
3 2
(2) 2 2 3 2 17 2 30 p
16 12 34 30 0
is a factor of p(x)
( 2) x
Now,
2
( ) ( 2)(2 + - 15) p x x x x
2
= ( - 2)(2 + 6 - 5 -15)x x x x
= ( - 1){2 ( + 3) - 5( + 3)}x x x x
= ( - 1)( + 3)(2 - 5)x x x
(ii) Given that
3 2
( ) 6 11 6 p x x x x
3 2
(1) 1 6 (1) 11 1 6 p
1 6 11 6 0

is a factor of p(x)
( 1) x
Now,
2
( ) ( 1)( 5 6) p x x x x
2
( 1)( 3 2 6) x x x x
( 1){ ( 3) 2( 3)} x x x x
( 1)( 2)( 3) x x x
(iii) Given that
3 2
( ) 4 4 p x x x x
3 2
( 1) ( 1) ( 1) 4( 1) 4 p
1 1 4 4 0
is a factor of p(x)
( 1) x

Now,
2
( ) ( 1)( 4) p x x x
2 2
( 1)( 2 ) x x
( 1){( 2)( 2)} x x x
( 1)( 2)( 2) x x x
(iv) Given that
3 2
( ) 3 3 1 p x x x x
3 2
(1) 3(1) (1) 3(1) 1 p
3 1 3 1 0
is a factor of p(x)
( 1) x
(iv) Given that
2
( ) ( 1)(3 2 1) p x x x x

2
( 1)(3 3 1) x x x x
( 1){3 ( 1) 1( 1)} x x x x
( 1)( 1)(3 1) x x x
Question: 25
Using suitable identity, evaluate the following:
(i)
3
103
(ii)
101 102
(iii)
2
999
Solution:
(i)
3
103
3
100 3
3 3
100 3 3 100 3(100 3)
1000000 27 90000 2700
1092727
(ii)
101 102
100 1 100 2
10000 200 100 2
10302
(iii)
2
999

2
1000 1
2
1000 1 2000
1000000 1 2000
1000001 2000
998001
Question: 26
Factorise the following:
(i)
2
4 20 25 x x
(ii)
2 2
9 – 66 121y yz z
(iii)
2 2
1 1
2
3 2
x x
Solution:
(i)
2
4 20 25 x x
2
2
2 2.5.2 5 x x
2
2 5 x
(ii)
2 2
9 – 66 121y yz z
2 2
3 11 2.3 .11 y z y z
2
3 11 y z
(iii)
2 2
1 1
2
3 2
x x

1 1 1 1
2 2
3 2 3 2
x x x x
1 1 1
3 2
6 3 2
x x x
1 5
3
6 6
x x
Question: 27
Factorise the following:
(i)
2
9 – 12 3x x
(ii)
2
9 – 12 4x x
Solution:
(i)
2
9 – 12 3x x
2
3 3 4 1 x x
2
3 3 3 1 x x x
3 – 1 3 – 1 x x
(ii)
2
9 – 12 4x x
2
2
3 2.2.3 2 x x
2
3 2 x
3 2 3 2 x x
Question: 28

Expand the following:
(i)
2
4 – 2a b c
(ii)
2
3 – 5 –a b c
(iii)
2
– 2 – 3x y z
Solution:
(i)
2
4 – 2a b c
2 2
2
4 2 2.4 2. .2 2.2 .4 a b c ab b c c a
2 2 2
16 4 8 4 16 a b c ab bc ca
(ii)
2
3 – 5 –a b c
2 2
2
3 5 ( ) 2.3 .5 2.5 . 2.3 . a b c a b b c a c
2 2 2
9 25 – 30 10 6 a b c ab bc ac
(iii)
2
– 2 – 3x y z
2 2 2
2 3 2. .2 2.2 .3 2.3 . x y z x y y z z x
2 2 2
4 9 – 4 – 12 6 x y z xy yz xz
Question: 29
Factorise the following:
(i)
2 2 2
9 4 16 12 16 24 x y z xy yz xz
(ii)
2 2 2
25 16 4 40 16 20 x y z xy yz xz

(iii)
2 2 2
16 4 9 16 12 24 x y z xy yz xz
Solution:
(i)
2 2 2
9 4 16 12 16 24 x y z xy yz xz
2 2 2
3 2 4 2.3 .2 2.2 .4 2.4 .3 x y z x y y z z x
2
3 2 4 x y z
3 2 4 3 2 4 x y z x y z
(ii)
2 2 2
25 16 4 40 16 20 x y z xy yz xz
2 2 2
5 4 2 2.5 .4 2.4 .2 2.5 .2 x y z x y y z x z
2
5 4 2 x y z
5 4 2 5 4 2 x y z x y z
(iii)
2 2 2
16 4 9 16 12 24 x y z xy yz xz
2 2 2
4 2 3 2.4 .2 2.2 .3 2.3 .4 x y z x y y z z x
2
4 2 3 x y z
4 2 3 4 2 3 x y z x y z
Question: 30
If and , find
9 a b c
26 ab bc ca
2 2 2
a b c
.
Solution:
Given,
9 a b c
26 ab bc ca

We know that,
2 2 2
2
2 a 2 a b c a b c ab bc ca
2
2 a b c ab bc ca
2
9 2 26
81 52
29
Question: 31
Expand the following:
(i)
3
3 2a b
(ii)
3
1
3
y
x
(iii)
3
1
4
3
x
Solution:
(i)
3
3 2a b
3 3
3 2 3.3 .2 . 3 2 a b a b a b
3 3
27 8 18 3 2 a b ab a b
3 3 2 2
27 8 54 36 a b a b ab
(ii)
3
1
3
y
x

3 3
1 1 1
.
3 3
3.
3
y y y
x x x
3 2
3 2 2
1 3 3
27 3 9
y y y
x x x
3 2
3 2
1
27 3
y y y
x x x
(iii)
3
1
4
3
x
3
3
1 1 1
4 3.4. 4
3 3 3
x x x
3 2
1 48 12
64
27 3 9
x x x
3 2
1 16 4
64
27 3
x x x
Question: 32
Factorise the following:
(i)
3 2
1 64 12 48 a a a
(ii)
3 2
12 6 1
8
5 25 125
p p p
Solution:
(i)
3 2
1 64 12 48 a a a
3 3
1 4 3.1.4 1 4 a a a
3
1 4a
1 4a 1 4a 1 4a

(ii)
3 2
12 6 1
8
5 25 125
p p p
3
3
1 1 1
2 3 2 (2 )
5 5 5
p p p
3
3 3 3
1
2 [( ) 3 ( )]
5
p a b a b ab a b
1 1 1
2 2 2
5 5 5
p p p
Question: 33
Find the following products:
(i)
2
2
2 4
2 4
x x
y xy y
(ii)
2 4 2
1 1 xx x
Solution:
(i)
2
2
2 4
2 4
x x
y xy y
3
2 2 2
2 3
4 2
2 8
2 2 2 4
x x y xy x y
xy y
3
3
2
2
x
y
3
3
8
8
x
y
(ii)
2 4 2
1 1 x x x

6 2 2 4 2
1 x x x x x
6
1 x
Question: 34
Factorise:
(i)
3
1 64 x
(ii)
3 3
2 2a b
Solution:
(i)
3
1 64 x
3
3
1 4 x
2
2
1 4 1 1.4 4
x x x
2
1 4 1 4 16 x x x
(ii)
3 3
( 2 )a b
2
2
2 2 2
a b a ab b
2 2
2 2 2 a b a ab b
Question: 35
Find the following product:
2 2 2
2 3 4 9 2 3 6 x y z x y z xy yz xz
Solution:
2 2 2
2 – + 3 4 + + 9 + 2 + 3 – 6x y z x y z xy yz xz

3 2 2 2 2
8 2 18 4 6 12 x xy xz x y xyz x z
2 3 2 2 2
4 9 2 3 6 x y y yz xy y z xyz
2 2 3 2 2
12 3 27 6 9 18 x z y z z xyz yz xz
3 3
8 18 27 x xyz y z
Question: 36
Factorise:
(i)
3 3 3
8 64 24 a b c abc
(ii)
3 3 3
2 2 8 27 18 2 a b c abc
Solution:
(i)
3 3 3
8 64 24 a b c abc
3 3 3
8 64 24 a b c abc
3 3
3
2 4 3. .2 .4 a b c a b c
2 2 2
2 4 4 16 2 8 4 a b c a b c ab bc ac
(ii)
3 3 3
2 2 8 27 18 2 a b c abc
3
3 3
2 2 3 3. 2 .2 .3 a b c a b c
2 2 2
2 2 3 2 4 9 2 2 6 3 2 a b c a b c ab bc ac
Question: 37

Without actually calculating the cubes, find the
value of:
(i)
3 3 3
1 1 5
2 3 6
(ii)
3 3 3
0.2 – 0.3 + 0.1
Solution:
(i) Give that:
3 3 3
1 1 5
2 3 6
Let and
1 1
,
2 3
ba
c=
5
6
1 1 5 3 2 5 0
0
2 3 6 6 6
a+b +c =
3 3 3 2 2 2
a +b +c - 3abc = (a+b +c)(a +b +c - ab - bc - ca)
3 3 3 2 2 2
a +b +c - 3abc = (0).(a +b +c - ab - bc - ca)
3 3 3
a +b +c - 3abc = 0
3 3 3
a +b +c = 3abc
3 3 3
1 1 5 1 1 5 5
3
2 3 6 2 3 6 12
(ii) Give that,
(0.2)
3 3 3
(0.3) (0.1)
Let and
0.2, 0.3 ba
c= 0.1

0.3 0.1 0.3 0.3 0 a+b +c = 0.2
3 3 3 2 2 2
a +b +c - 3abc = (a+b +c)(a +b +c - ab - bc - ca)
3 3 3 2 2 2
a +b +c - 3abc = (0).(a +b +c - ab - bc - ca)
3 3 3
a +b +c - 3abc = 0
3 3 3
a +b +c = 3abc
(0.2)
3 3 3
(0.3) (0.1) 3(0.2)(0.3)(0.1) 0.018
Question: 38
Without finding the cubes, factorise:
3 3 3
– 2 2 – 3 3 – x y y z z x
Solution:
3 3 3
– 2 2 – 3 3 – x y y z z x
Let
2 a x y
2 3 b y z
3 c z x
2 2 3 3 0 x y y z z x
0 a b c
then,
3 3 3
3 a b c abc
thus,
3 3 3
2 2 3 3 x y y z z x
2 2 3 33 x y y z z x
Question: 39
Find the value of:

(i) , when
3 3
– 12 64 x y xy
– 4 x y
(ii) ,when
3 3
– 8 – 36 – 216x y xy
2 6 x y
Solution:
3 3
– 12 64 . i x y xy
Given:
4 x y
We know that
3
3 3
3 x y x y xy x y
therefoureq (i) can be written as
3
3 12 64 x y xy x y xy
Putting the value of as , we get
x y
4
3
4 3 4 12 64 xy xy
=0
3 3
ii – 8 – 36 – 216 . ix y xy
Given:
2 6 x y
Therefoureq (i) can be written as
3
3
2 36 216 x y xy
2
2
2 2 2 36 216 x y x x y y xy
2 2
6 2 4 36 216 x xy y xy
2 2
6 12 24 36 216 x xy y xy

2 2
6 4 4 216 x xy y
2
6 2 216 x y
2
6 6 216
216 216
=0
Question: 40
Give possible expressions for the length and breadth
of the rectangle whose area is given by .
–
2
4 4 3a a
Solution:
Area of rectangle
–
2
4 4 3 a a
2
4 6 2 3 a a a
2 2 3 1 2 3 a a a
2 1 2 3 a a
The length and the breadth
–2 1 a
2 3 a
EXERCISE: 2.4
Question: 1
If the polynomials and
–
3 2
4 3 4 az z z
–
3
4 z z a
leave the same remainder when divided by
, find the value of a.
– 3z
Solution:

Let and
3 2
4 3 4 p z az z z
3
4 q z z z a
when p(z) and q(z) are divided by (z − 3)
then their remainders are equal i.e., p(3) = q(3).
By remainder theorem,
3 2 3
3 4 3 3 3 4 3 4 3 a a
27 36 9 4 27 12 a a
27 41 15 a a
26 26 a
1 a
Question: 2
The polynomial
4 3 2
– 2 3 p x x x x
We divided by leaves the remainder 19.
1x
Find the value of a.
Also find the remainder when p(x) is divided by
.
2x
Solution:
4 3 2
– 2 3 – 3 – 7 p x x x x ax a
When p(x) is divided by , the remainder is 19.
1x
∴ By remainder theorem
1 19 p
4 3 2
1 2 1 3 1 1 3 7 19 a a
1 2 3 3 7 19 a a
6 4 7 19 a
4 19 1 a

20
5
4
a
4 3 2
2 3 5 8 p x x x x x
When p(x) is divided by then the remainder by
2x
remainder theorem is
4 3 2
2 2 2 2 3 2 5 2 8 p
16 16 12 10 8
62
Hence, the value of a is 5 and remainder is 62.
Question: 3
If both and are factors of
– 2x
-
1
2
x
, show that .
2
5 px x r
p r
Solution:
Let
2
5 p x px x r
is factor of p(x)
2x
By factor theorem,
2 0p
2
2 5 2 0 p r
4 10 ...... r p i
is a factor of p(x)
1
2
x
2
1 1
5 0
2 2
p r

5
0
4 2
p
r
10 4
0
4
p r
10 4 0 p r
4 10 r p
10
......
4
p
r ii
From eqn. (i) and (ii)
10
4 10
4
p
p
16 40 10 p p
15 10 40 p
30
15
p
2 p
Substituting the value of p in (i)
4 2 10 r
2 r
Hence,
p r
Question: 4
Without actual division, prove that
is divisible by
4 3 2
2 5 2 2 x x x x
2
3 2 x x
Solution:
Let
4 3 2
2 5 2 2– – p x xx x x

2
3 2– g x x x
1 2 x x
4 3 2
1 2 1 5 1 2 1 1 2 p
2 5 2 1 2
0
is a factor of p(x)
1 x
By factor theorem,
4 3 2
2 2 2 5 2 2 2 2 2 p
32 40 8
0
are factor of p(x)
1 2, x x
or is a factor of p(x)
1 2 x x
2
3 2 x x
Question: 5
Simplify
3 3
2 5 2 5 x y x y
Solution:
3 3
2 5 – 2 + 5x y x y
2
=[(2 5 ) (2 + 5 )][(2 5 ) + x y x y x y
2
(2 5 )(2 + 5 )+ (2 + 5 ) ]x y x y x y
3 3 2 2 2 2 2
[ = ( )( + b + ),( + ) = ( + 2 + ), a b a b a a b a b a ab b
and
2 2 2
( ) = ( 2 )] a b a ab b
2 2
( 10 )[(4 + 25 20 )+ x y xyy

2 2 2 2
(4 25 ) + (4 + 25 + 20 )]x y x y xy
2 2
( 10 )[12 + 25 ] y x y
2 3
120 250 x y y
Question: 6
Multiply
by
2 2 2
+ 4 + + 2 + – 2 2 x y z xy xz yz z x y
Solution:
2 2 2
4 2 2 2 x y z xy xz yz z x y
2 2
2
2 2
2
2
x y z x y
x y z
y z z x
3 3
3
2 3 2 x y z x y z
3 3 3
8 6 x y z xyz
Question: 7
If a, b, and c are all non-zero and prove
0 a b c
that .
2 2 2
3
a b c
bc ca ab
Solution:
LHS
2 2 2
a b c
ca
bc ab
3 3 3
a b c
abc

2 2 2
( )( ) 3
a b c a b c ab bc ca abc
abc
[
3 3 3
a b c 3abc (a b c)
]
2 2 2
(a b c ab bc ca)
0.( )+3
2 2 2
a b +c ab bc ca abc
abc
[ a + b + c = 0]
3
3
abc
= =
abc
= RHS
Question: 8
If and , then prove that
5 a b c
10 ab bc ca
3 3 3
– 3 – 25 a b c abc
Solution:
Give,
a+b +c = 5,ab +bc +ca = 10
2 2 2 2
2( ) (a+b +c) a b c ab bc ca
2 2 2 2
(5) 2(10) a b c
2 2 2
25 2(10) a b c
2 2 2
25 20 a b c
2 2 2
5 a b c
Now,
LHS,
3 3 3
3 a b c abc
( )( +b +c )
2 2 2
a+b +c a ab bc ca

(5)[5 ( )] ab +bc +ca
(5)(5 10)=5( 5)= 25
Hence, LHS=RHS
Question: 9
Prove that
3
3 3 3
– – – a b c a b c
3 a b b c c a
Solution:
LHS
3 3 3 3
(a b c) a b c
[
3 3 3 3
] ( ) (a b c) a b c
( )[( ) + + ]
2 2
( ) a b c a a b c a a a b c
[( )( +c )]
2 2
b c b bc
[Using the identity, and
=( )( )
3 3 2 2
a b a b a b ab
]
=( )( )
3 3 2 2
a b a b a b ab
( )[ + + +
2 2 2 2 2
2 2 2 b +c a b c ab bc ca a a ab +ac]
( )( +c )
2 2
b c b bc
( )[ +3 +3
2 2 2 2 2
3 3 ] b +c b c a ab ac b c bc
( )[3( +
2
)] b +c a ab ac bc
3( )[ ( + ( )] b +c a a b) c a b
3( )[( + )( )] b +c a c a b
= RHS
3 ( )( +a)( ) a b b +c c