
Lesson: Polynomials
Exercise: 2.1 (5)
Question: 1
Which of the following expressions are polynomials in
one variable and which are not? State reasons for your
answer.
2
x x
y
t
y
y
x y t
2
i 4 3 7
2
ii
iii 3 2
2
iv
10 3 50
v +
t
Solution:
2
x - x +
i 4 3 7
There is only one variable x with whole number
power. So, this is a polynomial in one variable.
y
2
ii 2
There is only one variable y with whole number
power. So, this is a polynomial in one variable.
t t
iii 3 2

There is only one variable, t. The power of t in 3 t is
1
. is not a whole number.
2
So, is not a polynomial.
1
2
3 2
t t
2
iv
2
There is only one variable . .
2
The power is not a whole number. Therefore, is not
a polynomial.
-1
2
y
y
y y
y
y
y
10 3 50
There are three variable; , and and their powers
are whole numbers. So, this is a polynomial in three
variables.
v x y t
x y t
10 3 50
There are three variable; , and and their powers
are whole numbers. So, this is a polynomial in three
variables.
v
x y t
x y t

Question: 2
Write the coefficients of in each of the following :
x
x x
x x
x
x x
2
2
i 2 +
2 3
ii 2
iii
i
π
2 3
2
v 2 1
Solution:
We can write as So,
the coefficient of is .
We can write as . So,
2
the coefficient of is .
Here, we see that the coefficient
x x x x
x
x x x x
x
2 2
i 2 2 1 .
2
1
2 3 2 3
ii 2 2 1
1
iii
2
of is
We can rewrite as .
Therefore, the coefficient of
.
is
x
x x x
x
2
iv 2 1 0 2
π
2
– 1
2
0.
Question: 3
Give one example each of a binomial of degree ,
and of a monomial of degree .
35
100

Solution:
and
x x
35 100
7 7 16
Question: 4
Write the degree of each of the following polynomials:
x x x
t
3 2
i 5 4 7
2
ii 4 – y
iii 5 7
iv 3
Solution:
i has the highest power in the given polynomial
which is .
Therefore, the degree of the polynomial is .
ii – has the highest power in the given polynomial
which is . Therefore, the degree of
x
y
3
5
3
3
2
2
the polynomial is .
iii 5 has the highest power in the given polynomial
which is . Therefore, the degree of the polynomial is .
iv There is no variable in the given polynomial.
Therefore, the degre
t
2
1 1
e of the polynomial is .0

Question: 5
Classify the following as linear, quadratic and cubic
polynomial:
x x
x x
y y
x
t
r
x
2
i
3
ii
2
iii + 4
iv 1
v 3
2
vi
3
vii 7
Solution:

has the highest power in the given polynomial
which is . Therefore, it is a quadratic polynomial.
has the highest power in the given polynomial
which is . Therefore, it is a cubic polynomi
x
x
i
3
i
3
2
2
i
al.
has the highest power in the given polynomial
which is . Therefore, it is a quadratic polynomial.
has the highest power in the given polynomial
which is . Therefore, it is a linear pol
y
x
2
iii
iv
2
1
ynomial.
has the highest power in the given polynomial
which is . Therefore, it is a linear polynom l.ia
t
v
1
has the highest power in the given polynomial
which is . Therefore, it is a quadratic polynomial.
has the highest power in the given polynomial
which is . Therefore, it is a cubic polyno
r
x
2
vi
2
3
vii
3 mial.
Exercise 2.2 (4)
Question: 1
Find the value of the polynomial at
x x
x
x
x
2
5 4 3
i 0
ii 1
iii 2
Solution:

(i) =
p(x)
x x
2
5 4 3
p(0) = 5(0) + 4(0)
2
+ 3
= 3
(ii) =
p(x)
x x
2
5 4 3
p(-1) = 5(-1) + 4(-1)
2
+ 3
= -5 + 4(1) + 3 = 2
(iii) =
p(x)
x x
2
5 4 3
p(2) = 5(2) + 4(2)
2
+ 3
= 10 +16 + 3 = 29
Question: 2
Find , and for each of the following
polynomials:
p p p
p y y y
p t t t
p x x
p x x x
0 1 2
2
i = 1
2 3
ii 2 t 2
3
iii
iv 1 1
Solution:

p y y y
p
p
p
2
i 1
2
0 0 0 1 = 1
2
1 1 1 1 1
2
2 2 2 + 1 3
p t t t
p
p
p
2 3
ii t 2 2
2 3
0 2 0 2 0 0 2
2 3
1 2 1 2 1 1
= 2 + 1 2 1 = 4
2 3
2 2 2 2 2 2
= 2 2 8 8 = 4
p x x
p
p
p
3
iii
3
0 0 0
3
1 1 1
3
2 2 8
p x x x
p
p
p
iv = 1 1
0 = 0 1 0 + 1 = - 1 1 = 1
1 = 1 1 1 + 1 = 0 2 = 0
2 = 2 1 2 + 1 = 1 3 = 3
Question: 3
Verify whether the following are zeroes of the
polynomial, indicated against them.
5
p x x x
p x x x
p x x x
p x x x
p x x x
p
p
x x x
m
x x m x
x x x
1
i 3 + 1,
3
4
ii 5 π,
2
iii 1, = 1, -1
iv = 1 2 , x = 1,
( ) l ,
l
1 2
2
( ) 3 -1, ,
3 3
2
2
v , 0
vi
vii
1
viii p = 2 + 1, =
2
Solution:

If is a zero of the polynomial
then should be
3
x p x x
p
p
x
p x x
-1
i = = 3 + 1
3
1
0.
1 1
= 3 1
3 3
= 1 + 1 = 0
1
Therefore, = is a zero of the polynomial
3
3 1.
If
5
5
5
x p x x
p
p
x
p x x
4
ii = is a zero of the polynomial = 5 - π
4
then , should be 0.
5
4 4
= 5 π = 4 - π
5
4
Therefore, is not a zero of the polynomial
5 π.
If and are zeros of polynomial
0
x x
p x x p p
p
p
x
p x x
iii = 1 = 1
2
= 1, then 1 and 1 should be .
2
At, 1 = 1 1 = 0.
2
At, 1 = 1 1 = 0.
Hence, = 1 and 1 are zeros of the
2
polynomial = 1.

If and are zeros of the polynomial
then and should be
Therefore and
are zeros of the poly
x x
p x x x p
p
p
x x
iv = 1 = 2
+1 2 , 1 2 0.
1 1 + 1 1 2 = 0 3 = 0.
2 = 2 1 2 2 3 0 0.
, = 1 2
nomial
p x x x
= 1 2 .
If is a zero of the polynomial
then should be zero
Here
Hence is a zero of the polynomial
x p x x
p
p
x p x x
2
2
2
v 0 = ,
0 .
, 0 = 0 = 0
, = 0 = .
then
Therefore is a zero of the po
If is a zero of the polynom
lynomi
l
a
a
l
i
m
x
m
x x m
m m
m
x
x x m
p
p
p
=
l
( ) = l p should be 0.
l
= l +m m m 0
l l
,
l
vi
( ) l
and are zeros of the
polynomial th
If
ne
x x
x xp
1 2
3 3
2
( = 3 1
ii
)
v

0.and should be
p p
p
p
1 2
3 3
2
1 1 1
3 1= 3 1 1 1 0 .
3
3 3
2
2 2
3 1 4 1 3.
3 3
Therefore, is a zero of the polynomial
but is not a zero of the
polynomial.
p
x
2
x x x
1
3
2
( ) 3 1,
3
1
If is a zero of the polynomial
2
then should be .
=
x p x x
p
p
viii 2 + 1
1
0
2
1 1
2 1 1 + 1 2.
2 2
Therefore, is not a zero of the polynomial
.
x
p x x
1
2
= 2 1

Question: 4
Find the zero of the polynomial in each of the
following cases:
p x x
p x x
p x x
p x x
p x x
p x x
p x x
i 5
ii 5
iii 2 5
iv 3 2
v 3
vi a , a 0
vii = c + d, c 0, c, are real numbers.
Solution:
p x x
p x
x
x
i 5
0
+ 5 0
5
Therefore, 5 is a zero of the polynomial
x
p x x
5.
p x x
p x
x
x
ii = 5
= 0
5 = 0
= 5
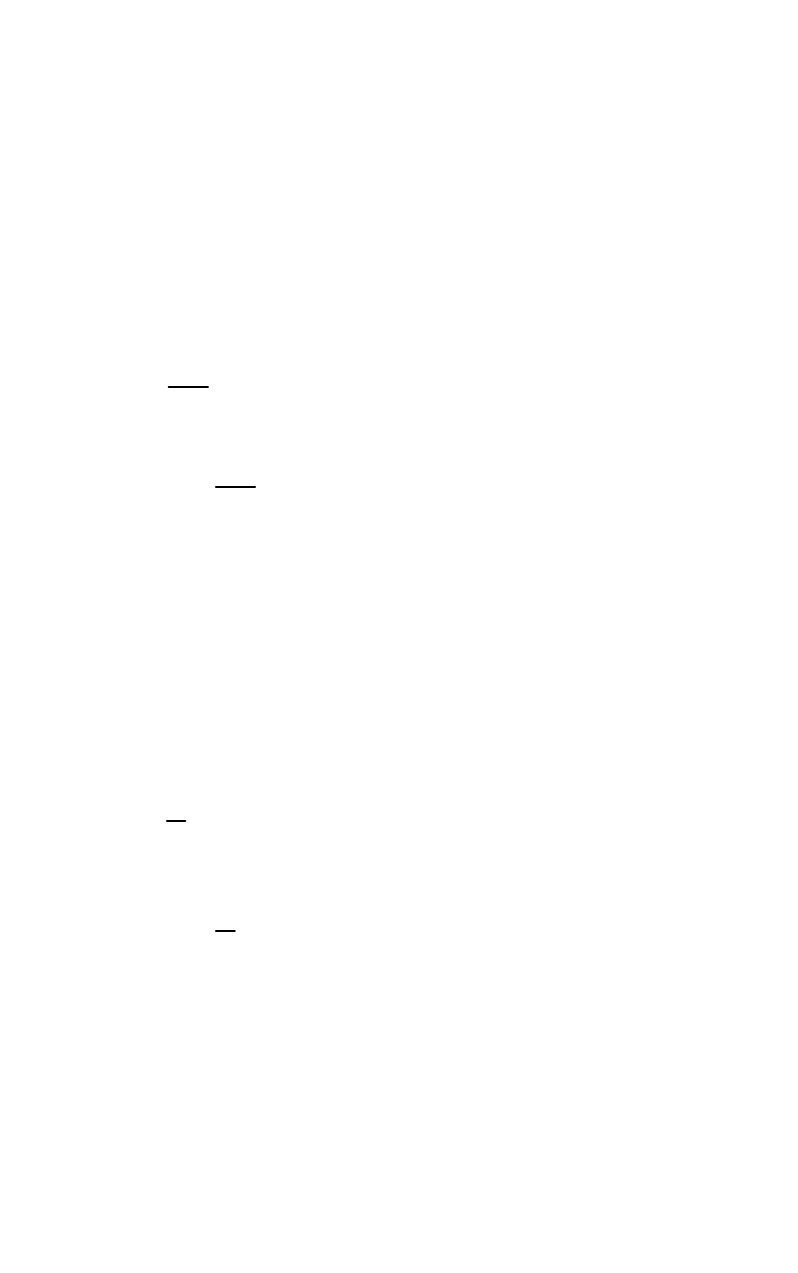
Therefore, 5 is a zero of the polynomial
5.
x
p x x
2 5
0
2 5 0
2 5
p x x
p x
x
x
x
iii
5
2
Therefore, is a zero of the polynomial
2 5.
x
p x x
5
2
p x x
p x
x
x
iv 3 2
= 0
3 2 0
2
3
2
Therefore, is a zero of the polynomial
3
x
p x x
= 3 2.
p x x
p x
x
x
v 3
0
3 0
0

Therefore, is a zero of the polynomial
x p x x
= 0 = 3 .
p x ax
p x
ax
x
vi =
= 0
= 0
= 0
Therefore, is a zero of the polynomial
.
x
p x ax
= 0
p x x
p x
x
-d
x
c
vii = c d
= 0
c + d = 0
Therefore, is a zero of the polynomial
.
x
p x cx d
d
c

Exercises 2.3 (3)
Question: 1
Find the remainder when
is divided by
x x x
x
x
x
x
x
3 2
3 3 1
i 1
1
ii
2
iii
iv π
v 5 2
Solution:
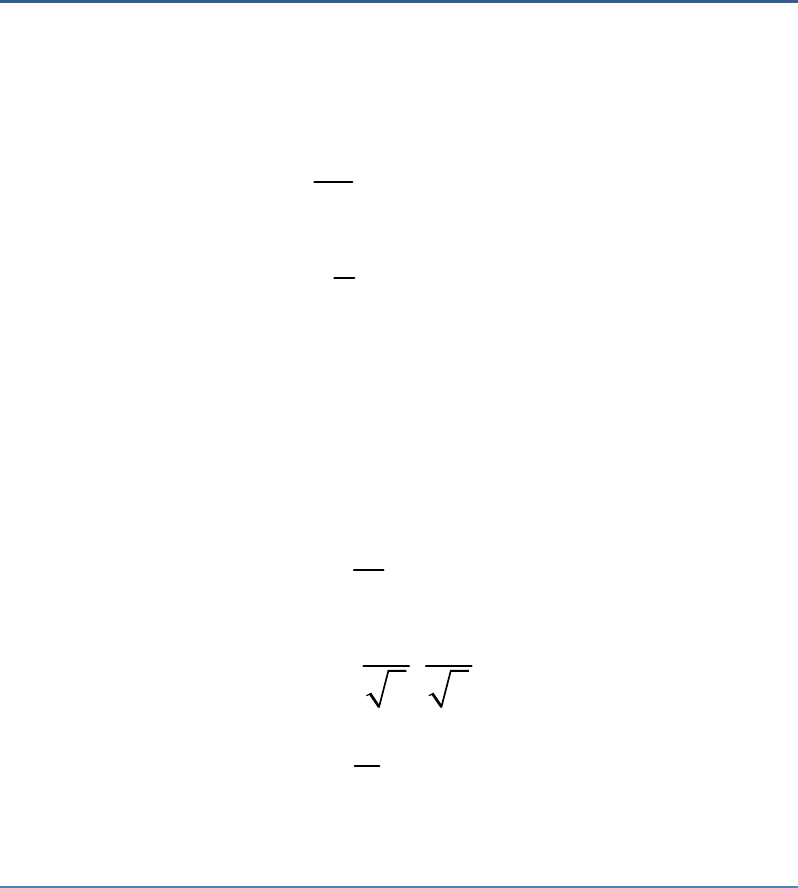
x
i + 1
By long division,
Therefore, the remainder is 0.
By long division,
x
1
ii
2
Therefore, the remainder is
27
.
8
x
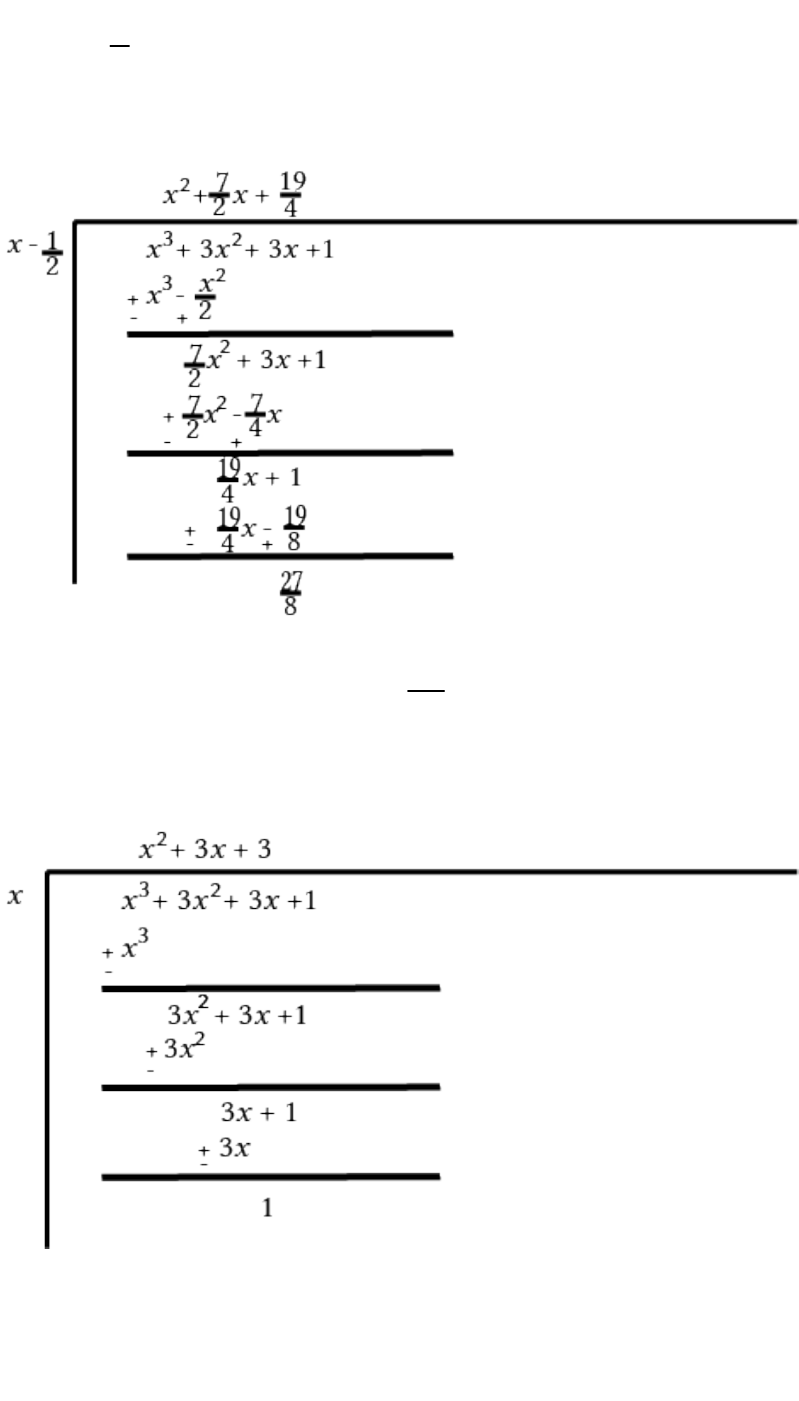
iii
Therefore, the remainder is 1.
x
iv π
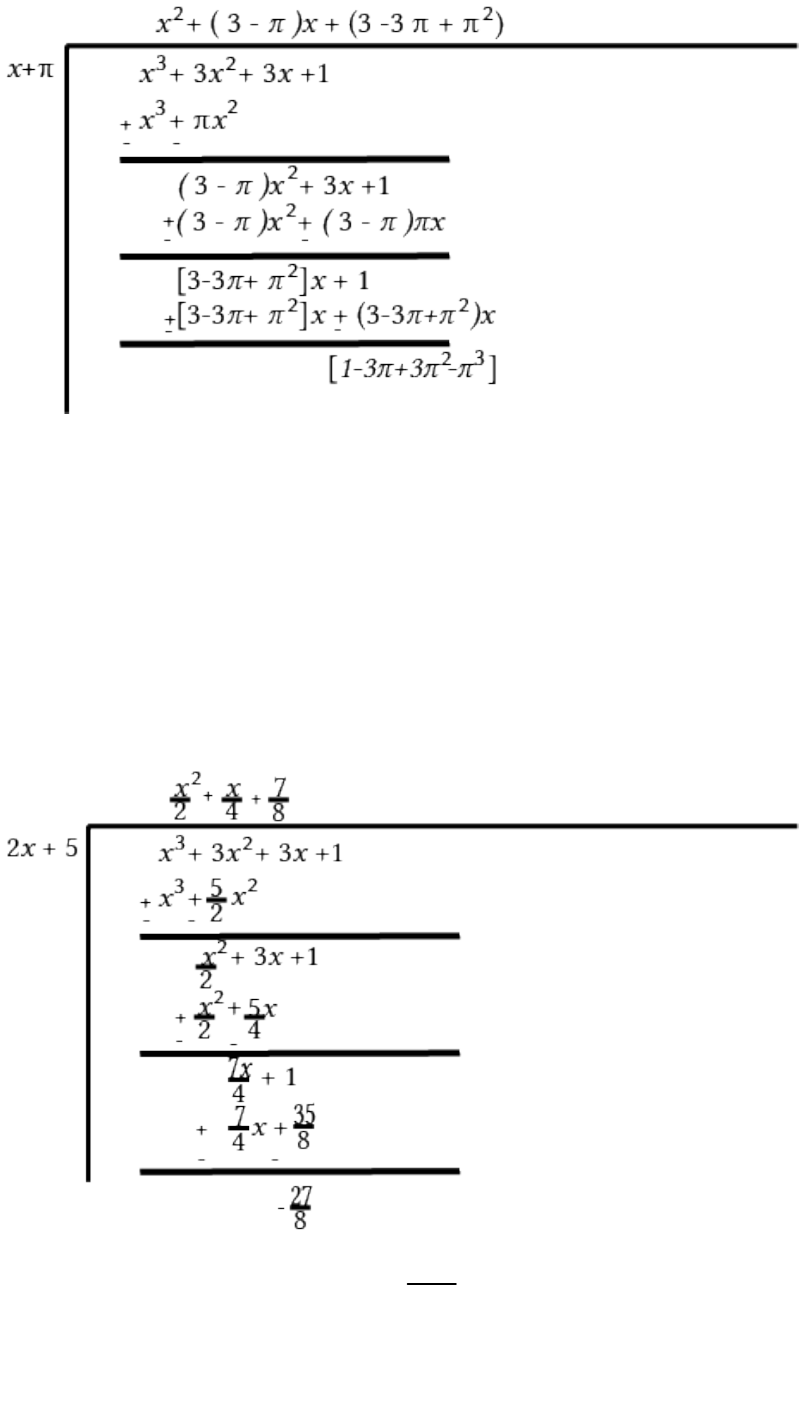
Therefore, the remainder is .
2 3
1 3π 3π π
x
v 5 2
Therefore, the remainder is
-27
.
8

Question: 2
Find the remainder when is divided
by .
x ax x a
x a
3 2
6
Solution:
By long division,
Therefore, the remainder obtained is
when is divided by .
a
x ax x x a
5
3 2
6 a

Question: 3
Check whether is a factor of .
x x x
3
7 3 3 7
Solution:
We have to divide If remainder
comes out to be 0 then 7 + 3x will be a factor
of
x x x
x x
3
3 + 7 by 7 + 3 .
3
3 + 7 .
By long division,
As the remainder is not zero, so is not a factor of
.
3
7 3
3 + 7
x
x x
Exercise 2.4
Question: 1

Determine which of the following polynomials has
a factor :
x
x x x
x x x x
x x
x x x
1
3 2
i 1
4 3 2
ii 1
4 3 2
iii + 3x + 3x + 1
3 2
iv 2 2 + 2
Solution:
If is a factor of
Therefore, is a factor of this polynomial.
x x x x x
x x x x
x
3 2
i 1 p = 1,
p 1 must be zero.
3 2
Here, p = + + + 1
3 2
p 1 1 + 1 1 1
1 1 1 1 0
+ 1

If is a factor of
must be zero.
Here
As, is not a facto
ii + 1
4 3 2
= 1,
1
,
4 3 2
= 1
4 3 2
1 1 1 1 1 + 1
1 1 1 1 1 1
1 0, 1
x
p x x x x x
p
p x x x x x
p
p x
r of
this polynomial
Therefore, is not a factor of this polynomial.
.
1
x
is a factor of polynomial
Ther
x
p x x x x x
p
p
p
x
iii If 1
4 3 2
= 3 3 1,
1 must be 0.
4 3 2
1 = 1 + 3 1 + 3 1 + 1 1
= 1 3 3 1 1 = 1
1 0.
Therefore, 1 is not a factor of this
polynomial.
efore, is not a factor of this polynomial.
x
1

If is a factor of polynomial
must be0
Therefore, is not a factor of this polynomial.
x
p x x x x
p
p
x
iv 1
3 2
= 2 2 2, p 1 .
3 2
-1 = 1 1 2 + 2 -1 2
= 1 1 2 2 2 2 2
1 0.
+ 1
Question: 2
Use the Factor Theorem to determine whether
is a factor of in each of the following cases
x
x
p x x x x x x
p x x x x x x
p x x x x x x
g
p :
3 2
i 2 2 1, g 1
3 2
ii 3 3 1, g 2
3 2
iii 4 6, g 3
Solution:

If is a factor of
the polynomial must be zero
p x p
p x x x x
p
x x
x
i
g x = x + 1
, 1 .
3 2
2 2 1
3 2
1 2 1 1 2 1 1
= 2 1 1 2 1 0
Hence,
g 1 is a factor of the given polynomial.
i If g
polynomial
x p x
p
p x x x x
p
x x
1 is a factor of ,
1 must be zero.
3 2
= 2 2 1
3 2
1 2 1 1 2 1 1
2 1 1 2 1 0
Hence,
g 1 is a factor of the given polynomial.
If is a factor of the given polynomial
must be
x x
p x p
p x x x x
p
p
x x
ii g = + 2
, 2 0.
3 2
+3 + 3 1
3 2
2 -2 + 3 - 2 + 3 - 2 + 1
8 + 12 6 1= 1
2 0
Hence,
g 2 is not a factor of the given polynomial.

If factor of given polynomial
must be
Therefore is a factor of the given
polynomial.
x x
p x p
p x x x x
p
x x
iii g = 3 is a
, 3 0.
3 2
= 4 6
3 2
3 = 3 4 3 3 6 27 36 9 0
, g 3
Question: 3
Find the value of , if is a factor of
in each of the following cases:
k x p x
p x x x k
p x 2x kx
p x kx x
p x kx x k
1
2
i
2
ii 2
2
iii 2 1
2
iv 3
Solution:
is a factor of the polynomial
Therefore, the value of is
x
p x x x k
p
k
k
k
k
i If 1
2
,
then,
1 0
2
1 1 0
2 0
= 2
2.

is a factor of the polynomial
then
Therefore, value of is
x
p x x kx
p
k
k
ii If - 1
2
2 2,
1 0
2
2 1 k 1 2 0
2 k 2 0
2 2 2 2
2 2 .
Therefore, the value of is
x
p x kx x
p
k
k
k
k
iii If - 1 is a factor of polynomial
2
2 1,
then,
1 0
2
1 2 1 1 = 0
2 1 0
2 1
2 1.

If is a factor of the polynomial
then,
Therefore, the value of is
x
p x kx x k
p
k k
k k
k
k
k
iv 1
2
3
1 0
1 3 1 = 0
3 0
2 3 0
3
2
3
.
2
Question: 4
Factorise:
x x
x x
x x
x x
2
i 12 7 1
2
ii 2 7 3
2
iii 6 5 6
2
iv 3 4
Solution:
x x
x x x
x x x
2
2
i 12 7 1
= 12 4 3 1
= 4 3 1 1 3 1
= 3x 1 4x 1

x x
x x x
x x x
x x
2
ii 2 7 3
2
2 6 3
2 3 1 3
3 2 1
x x
x x x
x
x x
2
iii 6 5 6
2
6 9 4 6
3x 2 3 2 2x + 3
2 3 3 2
x x
x x x
x x x
x x
2
iv 3 4
2
3 4 3 4
3 4 1 3 4
3 4 1
Question: 5
x x x
x x x
x x x
y y y
Factorise:
3 2
i 2 2
3 2
ii 3 9 5
3 2
iii 13 32 20
3 2
iv 2 2 1

Solution:
Let
Factors of are ± and ± .
By trial method,
we find that is the factor of .
Now,
Therefore, is the
p x x x x
x p x
p x x x x
p
x
3 2
i = 2 2
2 1 2
+1
3 2
= 2 2
3 2
1 1 2 1 1 2
1 2 1 2
0
+1
factor of .
p x
(i) Let p(x) = x
3
- 2x
2
- x + 2
Factors of 2 are ±1 and ± 2.
By trial method, we find that (x+1) is the factor
of p(x).
Now,
p(x) = x
3
- 2x
2
- x + 2
p(-1) = (-1)
3
- 2(-1)
2
- (-1) + 2 = -1 -2 + 1 + 2 = 0
Therefore, (x+1) is the factor of p(x).
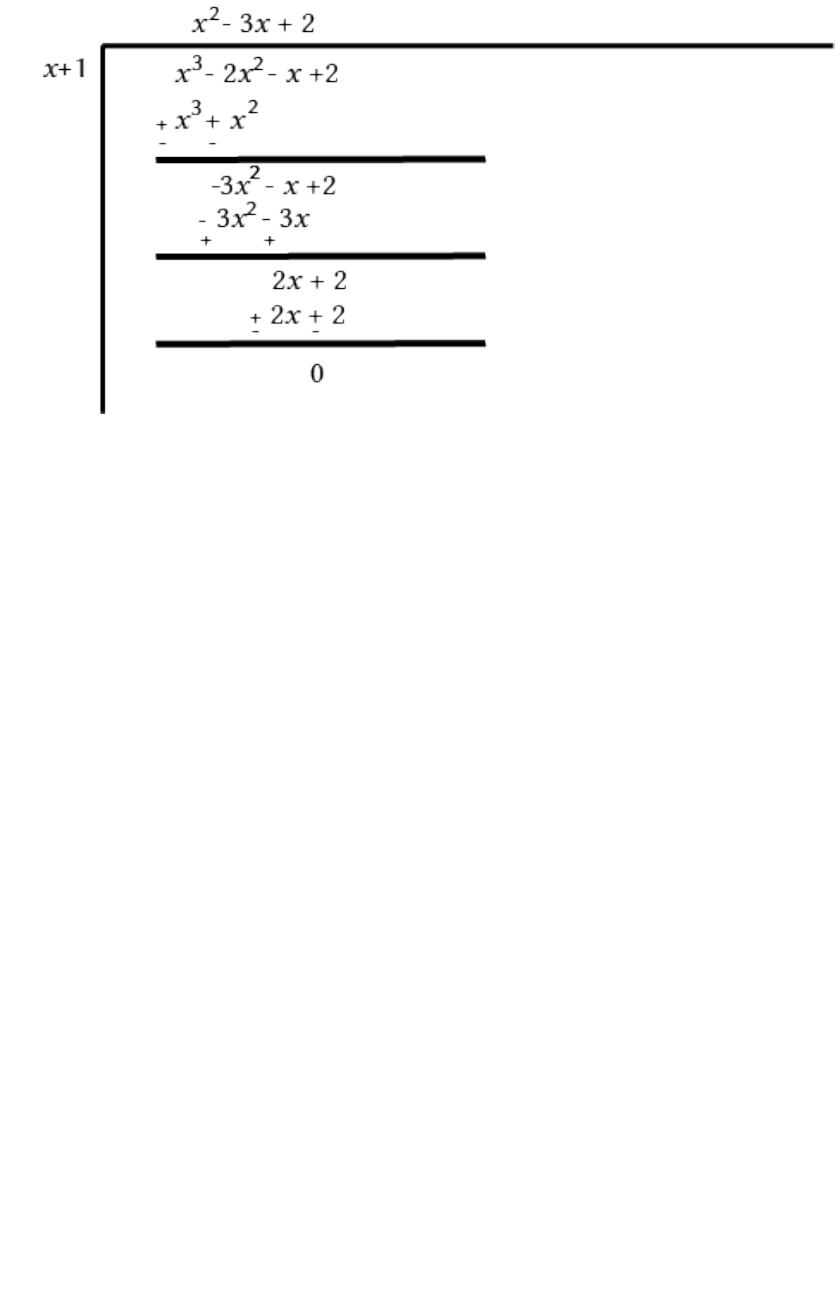
x x x
x x x x
x x x x
x x
Now, Dividend Divisor Quotient Remainder
2
1 3 2
2
+1 2 2
+1 1 2 1
x 1 1 2
Factors of are and
By trial method,
we find that is a factor of
p x x x x
x p x
p x x x x
p
x
3 2
ii Let = 3 9 5
5 ±1 ±5.
5 .
3 2
3 9 5
3 2
5 5 3 5 9 5 5
= 125 75 45 5 0
Therefore, 5 is a facto
( )
r of
p x
.
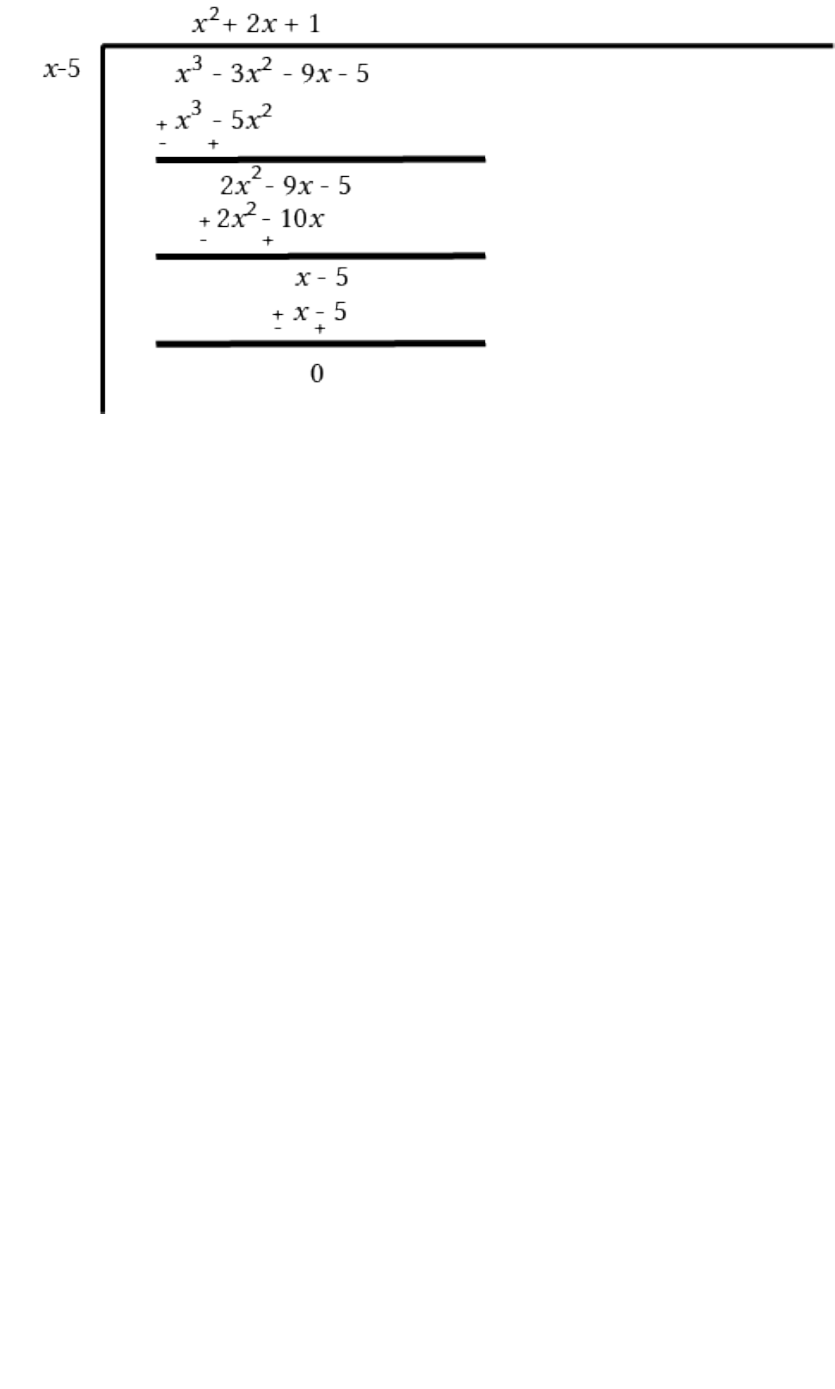
Now, Dividend Divisor Quotient Remainder
x x x
x x x x
x x x x
x x x
2
5 2 1
2
= 5 1
= 5 1 1 1
= 5 1 1
Factors of are and
By trial method,
we find that
So is factor of
Now,
p x x x x
p
x p x
p x x x x
p
3 2
iii Let 13 32 20.
20 ±1, ±2, ±4, ±5, ±10 ±20.
-1 0
, +1
3 2
= 13 32 20
3 2
-1 1 13 1 3
( )
2
)
1
(
Therefore, is a factor of
x p x
20
1 13 32 20 0
1 .

Now, Dividend Divisor Quotient Remainder
x x x
x x x x
x x x x
x x x
2
1 12 20
2
1 2 10 20
5 2 10 2
5 2 10
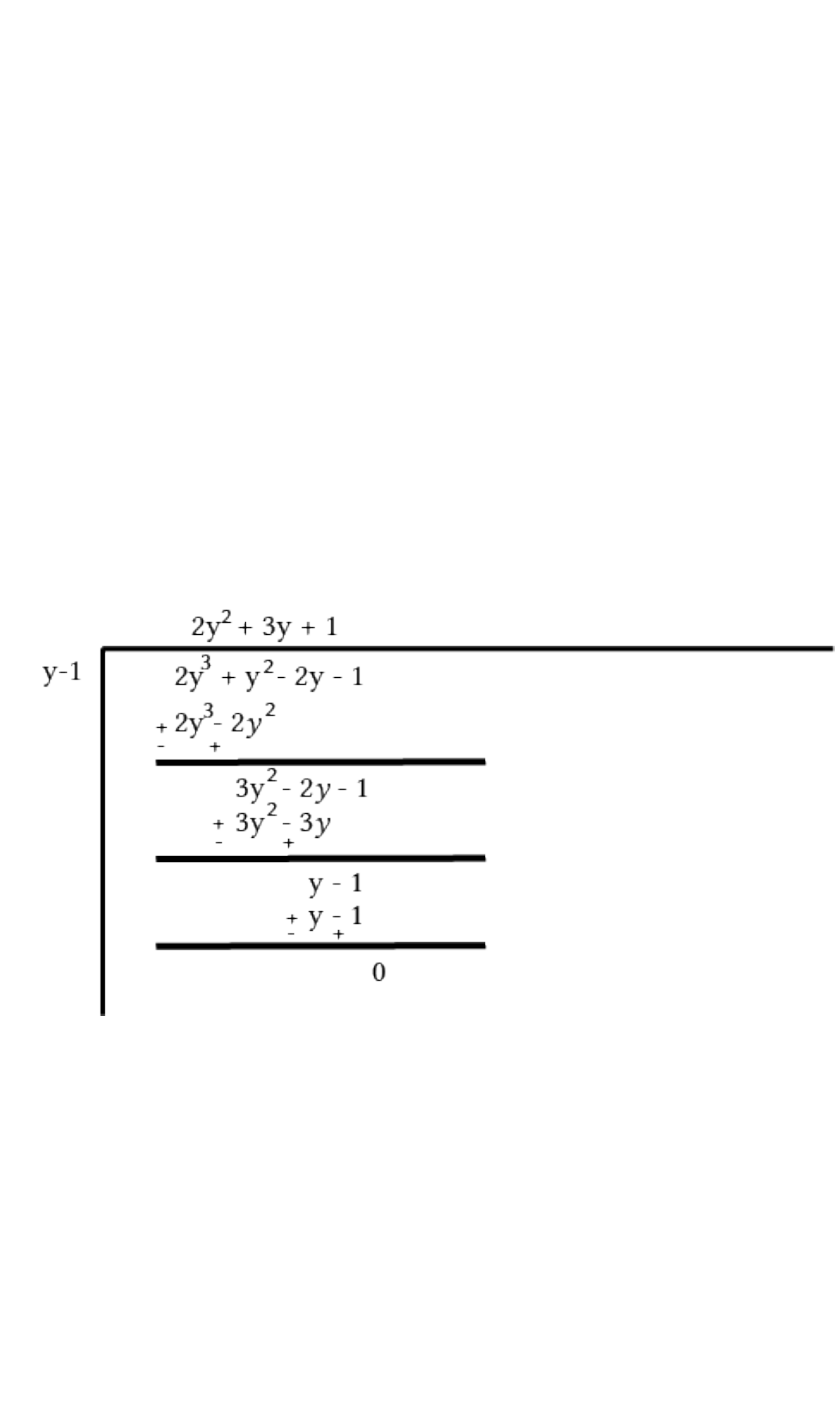
Let
Factors of are ± and ± .
By trial method, we find that
So, is factor of .
Now,
Therefore, is
p y y y y
p
y p y
p y y y y
y
3 2
iv 2 + 2 1
2 1 2
1 0
1
3 2
2 2 1
3 2
p 1 = 2 1 1 2 1 1
= 2 1 2
( )
(
1 0
1
)
a factor of .
y
p
Now, Dividend Divisor Quotient Remainder
y y y
y y y y
y y y y
y y y
2
1 2 3 1
2
= 1 2 2 1
= 1 2 1 1 1
= 1 2 1 1

Exercise 2.5
Question: 1
Use suitable identities to find the following products:
x x
x x
x x
y y
x x
2 2
i 4 10
ii 8 – 10
iii 3 4 3 – 5
3 3
iv
2 2
v 3 2 3 2
Solution:
dentity to be used:
.
x a x b x a b x ab
x x
x x x x
x x
i I
2
=
In 4 10 , a = 4 and b = 10.
Now,
2
4 10 = 4 10 4 10
2
= 14 40
dentity to be used:
Here and
x x
x x x x
a b
x x
x x
x x
x
ii 8 – 10
I
2
a b = a b ab.
, 8 – 10
8 – 10
2
= 8 – 10 8 – 10
2
= 8 – 10 – 80
2
=
x
2 – 80

dentity to be used:
.
Here,
is and
x x
x a x x a b x ab
x x a b
x x x x
x x
iii 3 4 3 – 5
I
2
b =
3 , = 4 5
2
3 4 3 – 5 3 4 5 3 4 5
2
9 3 4 5 20
x x
2
9 3 20
dentity to be used
.
:
y y
x x y x y
x y y
y
y
3 3
2 2
iv
2 2
I
2 2
y =
3
2
Here, and
2
3 3
2 2
y
2 2
2
2
3
2
=
2
9
4
= y
4

dentity to be u
.
.sed:
x x
x y x y x y
x y x
x x
x
x
v 3 2 3 2
2 2
I =
Here, 3 and 2
3 - 2 3 2
2
2
= 3 2
2
= 9 4
Question: 2
Evaluate the following products without multiplying
directly :
i 103 107
ii 95 96
iii 104 96
Solution:
Here,
Identitity to be used: .
.
x a b
x a x b x a b x ab
i 103 × 107 = 100 + 3 100 + 7
100, 3 and 7.
2
103 107 100 3 100 7
2
100 + 3 + 7 10 3 7
10000 100 2
1
11021

Identitity to be used:
x x b x b x b
x a b
ii 95 96 = 90 5 90 6
2
a = a a .
Here,
= 90, = 5 and = 4.
2
95 96 = 90 5 90 6 = 90 + 90 5 6 5 6
= 8100 11 90 + 30
= 8100 990 30
= 9120
Identitity to be used
.
:
x y x y x y
x y
iii 104 96 = 100 4 100 4
2 2
Here, = 100 and = 4.
104 96 100 4 100 4
2 2
= 100 4 10000 16 9984

Question: 3
Factorise the following using appropriate identities:
x xy y
y y
x y
2 2
2
2 2
i 9 6
ii 4 4 1
iii
100
Solution:
Using the identity,
,
x xy y x x y y
a b a ab b
a x b y
x xy y
x x y
x y y x y
2 2 2 2
i 9 + 6 = 3 + 2 3 +
2
2 2
2
3 and =
2 2
9 6
2 2
= 3 2 3 y
2
3 3x 3
,
y y y y
a b a ab b
y y y
y y
y y y
2
2 2
ii 4 4 1 2 2 2 1 1
2
2 2
Using the identity, = 2
2
a = 2 and b = 14 4 1
2
2
= 2 - 2 2 1 1
2
= 2 1 2 1 2 1
Using the identity,
y y
x x
a b a b a b
y
a x b
y y
x x
y y
x x
2
2
2 2
iii =
100 10
2 2
Here, and
10
2
2
2 2
100 10
10 10
Question: 4

Expand each of the following, using suitable
identities
x y z
x y z
x y z
a b c
x y z
:
2
i + 2 + 4
2
ii 2 – +
2
iii – 2 + 3 + 2
2
iv 3 – 7 –
2
v – 2 + 5 – 3
a
2
1 1
vi b + 1
4 2
Solution:
Using the identity,
,
and .
x y z
2
2 2 2
a b c = a b c 2ab 2bc 2ca
a x b= y c z
x y z x z x y
y z z x
x y
2
i 2 4
, 2
( )
4
2 2 2
2
2 4 = 2y 4 2 2
2 2 4 2 4
2 2
= 4
z xy yz xz
2
16 4 16 + 8

,
and .
x y z
a b c a b c ab bc ca
a x b c z
x y z x y z x y
y z z x
x
2
ii 2 –
Using the identity,
2
2 2 2
2 2 2
= 2 , = y =
2 2 2
2
2 – 2 2 2
+ 2 + 2 2
2
4 +
y z xy yz xz
2 2
4 2 4
Using the identity,
,
2
x y z
a b c = a b c ab bc ca
a x b y c
z x y z x y
x y y z z x
x y z xy
iii – 2 3 2
2
2 2 2
2 2 2
2 , = 3 and 2.
2 2 2 2
– 2 3 2 -2 3 2z
+ 2 2 3 + 2 3 2 + 2 2 2
2 2 2
= 4 9 4 12
yz xz
12 8
Using the identity
,
.
a b c
a b c a b c ab bc ca
a a b b c c
a b c a b c
a b b c c a
a
2
iv 3 – 7 –
,
2
2 2 2
2 2 2
3 , 7 and
2 2 2 2
3 – 7 – = 3 + 7 + +
2 3 -7 + 2 7 + 2 3
2
9 4
b ab bc ac
2 2
9 c 42 14 6

Using the identity,
and
x y z
a b c a b c ab
bc ca
a x b y c
x y z x y z
x y z z - x
2
v – 2 + 5 – 3
2
2 2 2
= + + + 2
+ 2 + 2
= 2 , = 5 = 3z.
2 2 2 2
– 2 + 5 – 3 = 2 + 5 3
2 2 5 2 5y 3 + 2 3 2
,
x y z xy yz xz
2 2 2
= 4 25 9 20 30 12
a b
a b c a b c
ab bc ca
a b b c
a b a
2
1 1
vi 1
4 2
2
2 2 2
Using the identity,
2 2 2
1 1
a, and = 1.
4 2
2 2
1 1 1
1
4 2 4
,
2 2
b
a b b a
a b ab b a
2
1
2
+ 1
2
1 1 1 1
2 + 2 1 + 2 1
4 2 2 4
1 1 1 1
1
16 4 4 2
Question: 5

:
Factorise
x y z xy yz xz
x y z xy yz xz
2 2 2
i 4 9 16 12 24 16
2 2 2
ii 2 8 2 2 4 2 8
Solution:
Using the identity,
,
i x y z xy yz xz
a b c a b c ab bc ca
x y z xy yz xz
x y z x y
y z z x
x y
2 2 2
4 9 16 12 24 16
2
2 2 2
2 2 2
2 2 2
4 9 16 12 24 16
2 2 2
2 3 4 2 2 3
2 3 4 2 4 2
2 3
z
x y z x y z
2
4
2 3 4 2 3 4
Using the identity,
,
x y z xy yz xz
a b c a b c ab bc ca
x y z xy yz xz
x y z x y
y z z x
2 2 2
ii 2 8 2 2 4 2 8
2
2 2 2
2 2 2
2 2 2
2 8 2 2 4 2 8
2 2
2
2 2 2 2 2
2 2 2 2 2 2 2
x y z
x y z x y z
2
2 2 2
2 2 2 2 2 2

Question: 6
–
x
a b
x
x
y
Write the following cubes in expanded form :
3
i 2 1
3
ii 2 3
3
3
iii 1
2
3
2
iv
3
Solution:
Using the identity,
,
x
a b a b ab a b
x x x x
x x x
x x x
3
i 2 1
3
3 3
3
3 3
3
2 1 2 1 3 2 1 2 1
3
8 1 6 2 1
3 2
8 12 6 1

–
Using the identity,
–
,
( ) ( )
a b
a b a b ab a b
a b a b a b a b
a b ab a b
a b a b ab
3
ii 2 3
3
3 3
3
3 3
3
2 3 2 3 3 2 3 2 3
3 3
8 27 18 2 3
3 3 2 2
8 27 36 54
Using the identity,
,
x
a b a b ab a b
x x x x
x x x
x x x
x
3
3
iii 1
2
3
3 3
3
3 3
3 3 3 3
3
1 1 3 1 1
2 2 2 2
27 9 3
3
1 1
8 2 2
27 27 9
3 2
1
8 4 2
27
3
8
x x
27 9
2
1
4 2

/
Using the identity,
,
( ) ( )
x y
a b a b ab a b
x y x y x y x y
x y xy x y x y x y xy
3
iv 2 3
3
3 3
3
3 3
2 2 2 2
3
3
3 3 3 3
8 2 8 4
3 3 3 3 2 2
2 2
27 3 27 3
Question: 7
Evaluate the following using suitable identities:
3
i 99
3
ii 102
3
iii 998
Solution:
Using the identity,
( ) ( )
a b a b ab a b
3 3
i 99 100 1
3
3 3
3
3
100 1
3 3
100 1 3 100 1 100 1
1000000 1 300 100 1
1000000 1 30000 300 970299

Using the identity,
,
( ) ( )
a b a b ab a b
3 3
ii 102 100 2
3
3 3
3
3
3 3
100 2 100 2 3 100 2 100 2
1000000 8 600 100 2 1000000 8 60000 1200
1061208
,
( ) ( )
a b a b ab a b
3
iii 998
Using the identity,
3
3 3
3
3
3 3
1000 2 1000 2 3 1000 2 1000 2
1000000000 8 6000 1000 2
1000000000 8 6000000 12000
994011992
Question: 8
Factorise each of the following :
a b a b ab
a b a b ab
a a a
a b a b ab
p
3 3 2 2
i 8 12 6
3 3 2 2
ii 8 12 6
3 2
iii 27 125 135 225
3 3 2 2
iv 64 27 144 108
1 9
3
v 27
216
p p
1
2
2 4

Solution:
Using the identity,
,
( )
a b a b ab
a b a b a b ab
a b a b ab a b a b a b
a b a b a b a b
3 3 2 2
i 8 12 6
3
3 3 2 2
3 3
2 2
3 3 2 2 3 3
8 12 6 2 3 2 3 2
3
2 2 2 2
Using the identity,
,
( )
a b a b ab
a b a b a b ab
a b a b ab a b a b a b
a b a b a b a b
3 3 2 2
ii 8 12 6
3
3 3 2 2
3 3
2 2
3 3 2 2 3 3
8 12 6 2 3 2 3 2
3
2 2 2 2
Using the identity,
,
a a a
a b a b a b ab
a a a
a a a
a a a a
3 2
iii 27 125 135 225
3
3 3 2 2
3 3
3 2
27 125 135 225
3 2 2
3
3 5 3 3 5 3 3 5
3
3 5 3 5 3 5 3 5

Using the identity,
,
3 3 2 2
3
3 3 2 2
3 3 2 2
3 3 2 2
3
iv 64 27 144 108
3 3
64 27 144 108
4 3 3 4 3 3 4 3
4 3 4 3 4 3 4 3
a b a b ab
a b a b a b ab
a b a b ab
a b a b a b
a b a b a b a b
Using the identity,
p p p
a b a b a b ab
p p p
p p p
p
p p p
1 9 1
3 2
v 27
216 2 4
3
3 3 2 2
3 3
1 9 1
3 2
27
216 2 4
3 2
1 1 1
3 2
3 3 3 3 3
6 6 6
3
1
3
6
1 1
3 3 3
6 6
1
6
Question: 9
Verify :
x y x y x xy y
x y x y x xy y
3 3 2 2
i
3 3 2 2
ii
Solution:

( )
x y x y x xy y
x y x y xy x y
x y x y xy x y
x y x y x y xy
x y
x y x y x y xy xy
3 3 2 2
i
3
3 3
3
3
3 3
3
2
3 3
3
Taking common
3 3 2 2
2 3
x y x y x y xy
3 3 2 2
We know that,
Taking common
( )
x y x y x xy y
x y x y xy x y
x y x y xy x y
x y x y x y xy
x y
x y x y x
3 3 2 2
ii
3
3 3
3
3
3 3
3
2
3 3
3
3 3 2
y xy xy
x y x y x y xy
2
2 3
3 3 2 2

Question: 10
Factorise each of the following :
y z
m n
3 3
i 27 125
3 3
ii 64 343
Solution:
Using the identity,
,
( ) ( ) ( )
y z
x y x y x xy y
y z
y z y z y y z z
y z y yz z
3 3
i 27 125
3 3 2 2
3 3
27 125
3 2
3 2
3 5 3 5 3 3 5 5
2
2
3 5 9 15 25
Using the identity,
( ) ( ) ( )
m n
x y x y x xy y m n
m n m n m m n n
m n m mn n
3 3
ii 64 343
3 3 2 2 3 3
64 343
3 2
3 2
4 7 4 7 4 4 7 7
2
2
4 7 16 28 49

Question: 11
Factorise :
x y z xyz
3 3 3
27 9
Solution:
Using the identity,
(
),
x y z xyz x y z xyz
x y z xyz x y z x y z
xy yz xz
x y z xyz
x y z x y z xy yz xz
x y
3
3 3 3 3 3
27 9 3 3 3
3 3 3 2 2 2
3
3 3 3
27 9
2
2 2
3 3 3 3
3
z x y z xy yz xz
2 2 2
9 3 3
Question: 12
Verify that :
x y z xyz
x y z x y y z z x
3 3 3
3
1
2 2 2
2
Solution:

( )
( )
x y z xyz
x y z x y z xy yz xz
x y z xyz x y z
x y z xy yz xz
x y z xy
x y z
yz xz
3 3 3
3
2 2 2
1
3 3 3
3
2
2 2 2
2
2 2 2
1
2 2 2 2
2
2 2
[
( ) ( )]
x y z x y xy
y z yz x z xz
x y y z
x y z
z x
1
2 2
2
2
2 2 2 2
2 2
2 2
1
2
2
Question: 13
If , show that .
x y z x y z xyz
3 3 3
0 3
Solution:

(
Now putting ,
)
x y z xyz x y z x y z
xy yz xz
x y z
x y z xyz x y z xy yz xz
x y z
3 3 3 2 2 2
3
0
3 3 3 2 2 2
3 0
3 3
xyz
3
3 0
Question: 14
Without actually calculating the cubes,
find the value of each of the following :
–
3 3 3
i 12 7 5
3 3 3
ii 28 15 13
Solution;
Let , and .
We observed that,
.
, ,
then
x y z
x y z
if x y z
x y z xyz
3 3 3
i 12 7 5
12 7 5
12 7 5 0
0
3 3 3
3
3 12 7 5 1260

–
Let = , and
We observed that,
if, ,
then,
x y z
x y z
x y z
x y z xyz
3 3 3
ii 28 15 13
28 15 13
28 15 13 0
0
3 3 3
3
3 28 15 13 16380
Question: 15
Give possible expressions for the length and breadth
of each of the following rectangles, in which their
areas are given:
Area :
Area :
a a
y y
2
i 25 35 12
2
ii 35 13 12
Solution:
Area :
a a
2
i 25 35 12
Since, area is product of length and breadth, therefore
by factorizing the given area, we can find the length
and breadth of a rectangle.

a a
a a a
a a a
a a
2
25 35 12
2
25 15 20 12
5 5 3 4 5 3
5 4 5 3
The possible expression for length .
The possible expression for breadth .
5 4
5 3
a
a
Area :
y y
y y
y y y
y y y
y y
2
ii 35 13 12
2
35 13 12
2
35 15 28 12
5 7 3 4 7 3
5 4 7 3
The possible expression for length
The possible expression for breadth
( ).
( ).
5 4
7 3
y
y
Question: 16
What are the possible expressions for the dimensions
of the cuboids whose volumes are given below?
Volume :
Volume :
x x
ky ky k
2
i 3 12
2
ii 12 8 20
Solution:
Volume :
x x
2
i 3 12

Since volume is product of length, breadth and height,
therefore by factorizing the given volume we can find
the length, breadth and height of the
cuboid.
x x x x
2
3 12 3 4
The possible expression for length .
The possible expression for breadth .
The possible expression for height ( ).
3
4
x
x
Volume :
ky ky k
2
ii 12 8 20
Since volume is product of length, breadth and height,
therefore by factorizing the given volume, we can find
the length, breadth and height of the cuboid.
ky ky k
k y y
k y y y
k y y y
k y y
2
12 8 20
2
4 3 2 5
2
4 3 5 3 5
4 3 5 1 3 5
4 3 5 1
The possible expression for length .
The possible expression for breadth
The possible expression for height
( ).
( ).
4
3 5
1
k
y
y