
Lesson: Areas of Parallelograms and Triangles
EXERCISE 9.1
Question: 1
The median of a triangle divides it into two
(a) Triangles of equal area
(b) Congruent triangles
(c) Right triangles
(d) Isosceles triangles
Solution:
a
Median of a triangle divides it into two triangles of
equal area.
Question: 2
In Fig. 9.3, which one of the figures has two polygons
on the same base and between the same parallels?

Solution:
d
In fig (D) two polygons PARQ and BSRQ lie on same
base QR and between same parallel lines PS and QR.
Question: 3
The figure obtained by joining the mid-points of the
adjacent sides of a rectangle of sides 8 cm and 6 cm
is:
(a) A rectangle of area 48 cm
2
.
(b) A square of area 48 cm
2
.
(c) A trapezium of area 24 cm
2
.
(d) A rhombus of area 24 cm
2
.
Solution:
d

Let PQRS be a rectangle with PQ=8cm and RQ=6cm.
Let ABCD be the quadrilateral formed by joining the
midpoints of sides PQ, QR, RS and SP, respectively.
Quadrilateral formed by joining the mid-points of the
adjacent sides of a rectangle is a rhombus.
Thus, ABCD is a rhombus.
Then, diagonal of the rhombus, AC= RQ=6cm and
BD=PQ=8cm.
∴ Area of rhombus ABCD=
Product of diagonals
cm
2
8 6
24
2 2

Question: 4
In Fig. 9.4, the area of parallelogram ABCD is:
(a)
AB BM
(b)
BC BN
(c)
DC DL
(d)
AD DL
Fig. 9.4
Solution:
c
Area of a parallelogram= base × corresponding
altitude.
Hence, for base AB, the height is DL.
So, area=AB×DL
Similarly, for base AD the height is BM.

So, area=AD×BM,
For base DC ,the height is DL.
So, area=DC×DL
And for base BC, the height is not given.
Hence, option (c) is correct.
Question: 5
In Fig. 9.5, if parallelogram ABCD and rectangle ABEM
are of equal area, then:
(a) Perimeter of ABCD = Perimeter of ABEM
(b) Perimeter of ABCD < Perimeter of ABEM
(c) Perimeter of ABCD > Perimeter of ABEM
(d) Perimeter of ABCD =
1
2
(Perimeter of ABEM)
Solution:
c
It is given that ABCD is a parallelogram,
∴AB=CD ……….. (i)
ABEM is a rectangle
∴
EM=AB ……… (ii)
Adding eq. (i) and eq. (ii), we get
AB+EM=CD+AB ….…… (iii)
In ∆AMD,
AD>AM …..(iv) (Hypotenuse is the longest side in a
right angled triangle)
Similarly, in ∆BEC
vBC BE ........
(Hypotenuse is the longest side in a
right angled triangle)
Adding Eq. (v) and Eq. (vi), we get

AD BC AM BE
Adding AB+CD on both sides,
Using Eq.
AD BC AB CD AM BE AB CD
AD BC AB CD AM BE AB EM iii
⇒ Perimeter of the parallelogram ABCD > Perimeter
of the rectangle ABEM.
Question: 6
The mid-point of the sides of a triangle along with any
of the vertices as the fourth point make a
parallelogram of area equal to
(a)
ar
1
( )
2
ABC
(b)
ar ( )
1
3
ABC
(c)
ar ( )
1
4
ABC
(d)
ar ( )ABC
Solution:
a

Let ABC is a triangle and D, E and F are the midpoints
of BC, AC and AB, respectively.
Then, Area (∆AFE) =Area (∆BFD) =Area (∆DEF) = Area
(∆EDC)
∴Area (∆DEF) =
1
4
Area (∆ABC)
Let BDEF be the parallelogram with vertices B as the
fourth point.
Then area of parallelogram BDEF
= Area (∆BFD) + Area (∆DEF)
=Area (∆DEF) + Area (∆DEF)
=2 Area (∆DEF)

=
Area ( )= Area ( )ΔABC ΔABC
1 1
2
4 2
Question: 7
Two parallelograms are on equal bases and between
the same parallels. The ratio of their areas is
(a) 1 ∶ 2
(b) 1∶ 1
(c) 2 ∶ 1
(d) 3 ∶ 1
Solution:
b

If two parallelograms are on equal bases and
between the same parallels then they are equal in
area.
Question: 8
ABCD is a quadrilateral whose diagonal AC divides it
into two parts, equal in area, then ABCD
(a) Is a rectangle
(b) Is always a rhombus
(c) Is a parallelogram
(d) Need not be any of (a), (b) or (c)
Solution:
d
Two triangles with equal areas doesn’t imply that
these triangles are also congruent.
Question: 9
If a triangle and a parallelogram are on the same base
and between same parallels, then the ratio of the
area of the triangle to the area of parallelogram is
(a) 1 ∶ 3

(b) 1 ∶2
(c) 3 ∶ 1
(d) 1 ∶4
Solution:
b
If a triangle and a parallelogram are on the same base
and between same parallels then
area of the triangle =
1
2
area of the parallelogram
Area of triangle
Area of paralleogram
1
2
⇒ Area of triangle∶ Area of parallelogram=1: 2
Question: 10
ABCD is a trapezium with parallel sides AB = a cm and
DC = b cm (Fig. 9.6). E and F are the mid-points of the
non-parallel sides. The ratio of Area (ABFE) and Area
(EFCD) is
(a) a ∶b
(b) (3a + b) ∶ (a + 3b)
(c) (a + b) ∶ (3a + b)
(d) (2a + b) ∶ (3a + b)

Solution:
b
Let us join DB which intersects EF at O.
Since E and F are the mid-points of AD and CB
respectively,
therefore,
.EF AB CD
So, the distance between AB, EF and EF, CD will be
same say h.
Now, in
ABD
,

E is the midpoint of AD and EO
∥
AB,
1 1
2 2
EO AB ia
and O is the midpoint BD.
Similarly, in
BCD
,
O and F are the midpoints of BD and BC respectively.
1 1
2 2
OF CD iib
Adding (i) and (ii),
1 1 1
2 2 2
EO OF a b a b iii
Now,
Area of a trapezium=
1
2
(Sum of the parallel lines)×(distance between
parallel lines)
So,
1 1
2 2
( ) ( )Area Trapezium ABFE a a b h
(Using (iii))
=
1
(3 )
4
a b h

And
ar Trapezium using(
1 1
2 2
)EFCD b a b h iii
=
1
(3 )
4
b a h
Hence,
ar(trapeziumABFE)
ar(trapeziumEFCD)
1
4
1
4
(3 )
(3 )
(3 ) (3 )
a b h
a b
b a h b a
EXERCISE 9.2
Question: 1
ABCD is a parallelogram and X is the mid-point of AB.
If Area (AXCD) =24 cm
2
, then Area (ABC) = 24 cm
2
.
Solution:
False,
Since X is the midpoint of AB,
= a ar BXC r AXC ar ABC i
1
2

Now, ∆ABC and parallelogram ABCD lie on same base
AB and between same parallel lines AB and CD,
a
a
1
2
1
2
[ ( ) ]
[ ]
1 1
24
2 2
ar ABC ar ABCD
r ABC r AXCD ar BXC
r ABC ar ABC
a
[∵
ar cm
2
( ) 24AXCD
is given and using (i)]
a
a
2
1
12
4
1
12
4
3
12
4
12 4
16
3
]r ABC ar ABC
r ABC ar ABC
ar ABC
ar ABC cm

Question: 2
PQRS is a rectangle inscribed in a quadrant of a circle
of radius 13 cm. A is any point on PQ. If PS = 5 cm,
then Area (PAS) = 30 cm
2
.
Solution:
PQRS is a rectangle inscribed in a quadrant of a circle.
Radius of circle= 13cm and PS=5cm
In right angled triangle ∆PQS,
cm
2 2 2 2
( ) ( ) (13) (5) 12PQ SQ QR
Now, Area (∆PQS)

2
1
2
1
2
1
5 12 30
2
base height
PS PQ
cm
So, the given statement is true, if A coincides with Q.
Question: 3
PQRS is a parallelogram whose area is 180 cm
2
and A
is any point on the diagonal QS. The area of
2
90 .ASR cm
Solution:
False,
It is given that
2
180ar gm PQRS cm
.
We know that diagonal of a parallelogram divides it
into two triangles of equal area.
r
2
( ) 90a QSR cm

Also,
Area of ∆ASR<Area of ∆QRS
2
90Area of ASR cm
Question: 4
ABC and BDE are two equilateral triangles such that
D is the mid-point of BC.
Then,
1
( ( )
4
)ar BDE ar ABC
.

Solution:
True,
It is given that D is the midpoint of BC.
So,
1
2
BD BC
Area of an equilateral trinagle= side)
2
3
( .
4
So,
ar BDE
ar ABC
2
2
2 2
2 2 2
2
3( )
( )
( ) ( ) 1
4 2
( ) ( ) 4( ) 4
3( )
4
BD BC
BD BC
BC BC BC
BC

Question: 5
In Fig. 9.8, ABCD and EFGD are two parallelograms
and G is the mid-point of CD. Then
1
)
2
( ) (ar DPC ar EFGD
.
Solution:
False
Let us join PG.

Since G is the midpoint of CD, in ∆DPC, PG is a
median.
So,
1
. 1
2
ar DPG ar GPC ar DPC
Now,
∆DPG and parallelogram EFGD lie on same base DG
and between same parallel lines EF and DG.
1
.. 2
2
ar DPG ar gm EFGD
From Eq. (1) and (2),
1 1
2 2
ar DPC ar gmEFGD
ar DPC ar gmEFGD

EXERCISE 9.3
Question: 1
In Fig.9.11, PSDA is a parallelogram. Points Q and R
are taken on PS such that
PQ = QR = RS and PA || QB || RC.
Prove that Area (PQE) = Area (CFD).

Solution:
It is given that PSDA is a parallelogram,
PS AD PQ AB
Also,
||PA QB
(given)
So, PABQ is a ∥gm.
PQ AB
….. (i) (Opposite sides of ∥gm)
Similarly, QRCB is a ∥gm.
∴QR=BC….. (ii) (Opposite sides of ∥gm)
And RSDC is a ∥gm.
∴RS=CD….. (iii) (Opposite sides of ∥gm)
Now, it is given that PQ = QR = RS…… (iv)
From Eq. (i), (ii), (iii) and (iv), we have
PQ QR RS AB BC CD
……… (v)
Now, in ∆PRF
and ||PQ QR QE RF
(Given)
So, by the midpoint theorem
PE EF
………. (vi)
Similarly, in
DEB
BC CD
(As proved above) and
||CF EB
(Given)
So, by the midpoint theorem
DF EF
……… (vii)
From (vi) and (vii)
PE DF
…………… (viii)
Now,
in and PQE DFC
PQ DC
(Using (v))
QPE FDC
(Alternate interior angle)

PE FD
(Using (viii))
So, by SAS congruence rule
PQE DCF
∴Area (∆PQE) = Area (∆DFC) (∵Congruent figures have
equal area)
Question: 2
X and Y are points on the side LN of the triangle LMN
such that LX = XY =YN. Through X, a line is drawn
parallel to LM to meet MN at Z (See Fig. 9.12). Prove
that Area (LZY) = Area (MZYX).

Solution:
Since ∆LXZ and ∆MXZ lie on same base XZ and
between same parallel lines LM and XZ.
Area (∆LXZ) = Area (∆XMZ)
On adding Area (∆XYZ) to both sides, we get
Area (∆LXZ) + Area (∆XYZ) = Area (∆XMZ) + Area
(∆XYZ)
Area (∆LYZ) = Area (MZYX)
Hence it is proved.
Question: 3
The area of the parallelogram ABCD is 90 cm
2
(see
Fig.9.13). Find
(i) Area (ABEF)

(ii) Area (
∆
ABD)
(iii)Area (
∆
BEF)
Solution:
(i) Parallelogram ABCD and parallelogram ABEF lie on
the same base AB and between the same parallel
lines AB and FC.
So, Area (ABEF) = Area (ABCD) = 90cm
2

(Parallelograms that lie on the same base and
between same parallel lines have equal area.)
(ii) Parallelogram ABCD and ∆ABD lie on the same
base AB and between the same parallel lines AB and
DC.
So, Area (∆ABD) =
1
2
Area (ABCD) =
1
2
×90cm
2
=45 cm
2
(If a triangle and a parallelogram lie on the same base
and between the same parallel lines then the area of
the triangle is equal to half of the area of the
parallelogram).
(iii) Parallelogram ABEF and ∆BEF lie on the same
base BE and between the same parallel lines BE and
FA.

So, Area (∆BEF) =
1
2
Area (ABEF) =
1
2
×90cm
2
=45
cm
2
(If a triangle and a parallelogram lie on the same base
and between the same parallel lines then the area of
the triangle is equal to half of the area of the
parallelogram).
Question: 4
In
ABC
, D is the mid-point of AB and P is any point
on BC. If
||CQ PD
meets AB in Q (Fig. 9.14), then
prove that
Area (
∆
BPQ) =
1
2
Area (ABC).

Fig. 9.14
Solution:
Let us join CD.
In
ABC
, CD is the median (Since D is the mid-point
of AB).
So, it will divide
ABC
into two triangles of equal
area.
.
..
ar BCD ar ABC
ar BDP ar DPC ar A C iB
( ) ( )
( )
1
2
1
( ) ( )
2
...( )

Now, ∆DPQ and ∆DPC are on the same base DP and
between the same parallels lines PD and QC.
( ) ( ) i. i ar DPQ ar DPC
From (i) and (ii),
(
1
( ) ( )
2
1
)
)
( (
2
)
ar BDP ar DPQ ar ABC
BPQ aar r ABC
Hence, it is proved.
Question: 5
ABCD is a square. E and F are respectively the
midpoints of BC and CD. If R is the mid-point of EF
(Fig. 9.15), prove that
Area (
∆
AER) =Area (
∆
AFR).

Fig. 9.15
Solution:
Since R is the midpoint of EF, AR is the median of
∆AEF.
Then, AR will divide ∆AEF into two triangles of equal
areas.
So, Area (AER) = Area (AFR)
Hence, it is proved.

Question: 6
O is any point on the diagonal PR of a parallelogram
PQRS (Fig. 9.16). Prove that
Area (
∆
PSO)= Area (
∆
PQO).
Fig. 9.16
Solution:
Let us join SQ which intersects PR at M.
M is the midpoint of SQ (∵Diagonals of a
parallelogram bisect each other)
So, in ∆PSQ, PM is a median.
∴ Area (∆PSM) = Area (∆PQM) ……… (i) (Median of a
triangle divides it into two triangles of equal areas).
Also, in ∆OSQ, OM is a median.
∴ Area (∆OSM) = Area (∆OQM) …... (ii) (Median of a
triangle divides it into two triangles of equal areas).
On adding (i) and (ii),
Area (∆PSM) + Area (∆OSM) = Area (∆PQM) + Area
(∆OQM)

⇒Area (∆PSO) = Area (∆PQO)
Hence it is proved.
Question: 7
ABCD is a parallelogram in which BC is produced to E
such that CE = BC (Fig. 9.17). AE intersects CD at F.
If Area (DFB) =3 cm
2
, find the area of the
parallelogram ABCD.
Fig. 9.17
Solution:

In ∆EAB, C is the midpoint of BE (∵BC=CE)
And CF
∥
AB (∵ABCD is a ∥gm)
So, by the midpoint theorem,
AF=FE…….. (i) and

1 1
2 2
FC AB CD
DF FC ii
Now, in
ADF
and
CFE
AD=CE (
∵
AD=BC=CE)
DF=FC (Using (ii))
AF=FE (Using (i))
So, by SSS congruence,
ADF ECF
Area Area ADF ECF
But,
2
3Area ADF Area DFB cm
(Since ∆ADF and ∆DFB lie on same base DF and
between same parallel lines DF and AB)
So,
2
3Area ECF cm
……… (iii)
Now, in
,FEB BC CE
(given)

∴FC is a median
Thus,
Area Area FCB ECF cm
2
3
... (iv) (Using (iii))
Now, ∆DCB and parallelogram ABCD lie on same base
DC and between same parallel lines DC and AB.
So,
+
1
2
2
2
2 3 3
2 6 1
(
Area DCB Area parallelogram ABCD
Area parallelogram ABCD Area DCB
Area parallelogram ABCD
Area DFB Area FCB Using iv
Area parallelogram ABCD
2
2cm
Question: 8
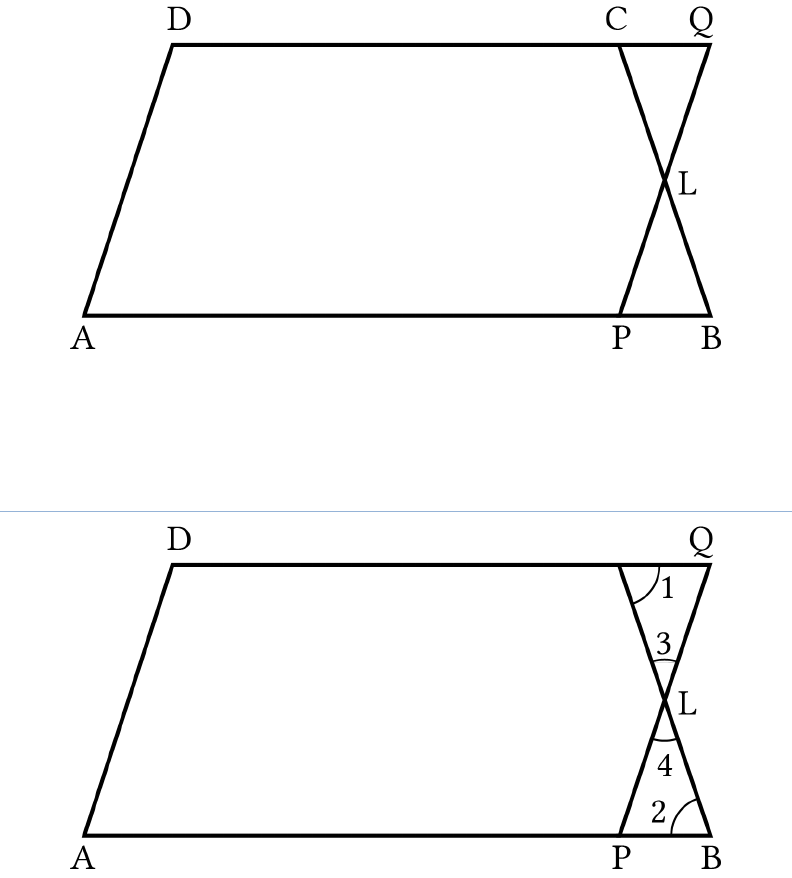
In trapezium ABCD, AB || DC and L is the mid-point of
BC. Through L, a line PQ || AD has been drawn which
meets AB in P and DC produced in Q
(Fig.9.18). Prove that
Area (ABCD) = Area (APQD).
Fig. 9.18
Solution:
In
and ,CLQ BLP
LQC LPB
(Alternate interior angles
as
AB DC AB DQ
)

LCQ LBP
(Alternate interior angles)
CL=LB (L is the midpoint of BC)
Thus,
BLPCLQ
(By AAS congruence rule)
∴ Area (∆CLQ) = Area (∆BLP) ….. (i) (Congruent
triangles have equal areas)
Now,
Area (ABCD) = Area (APLCD) + Area (BLP)
= Area (APLCD) + Area (CLQ)
(Using (i))
= Area (APQD)
Hence, it is proved.
Question: 9
If the mid-points of the sides of a quadrilateral are
joined in order, prove that the area of the
parallelogram so formed will be half of the area of the
given quadrilateral (Fig. 9.19).
[Hint: Join BD and draw perpendicular from A on BD.]

Fig. 9.19
Solution:
Let ABCD be a quadrilateral and P, F, R and S are the
midpoints of BC, CD, DA and AB, respectively.
We need to prove that
Area Area
1
2
PFRS ABCD

Let us join AP and AC.
AP divides ∆ABC into two triangles of equal area.
1
( ) ( ) ..... ( )
2
ar ABar ABP C i
Similarly, the median PS divides ∆ABP into two
triangles of equal area.
1
( ) ( ) ..... ( )
2
arar BSP ABP ii
From eq. (i) and (ii), we get

1
( ) ( ) ..... ( )
4
ar ar ABS B iP C i i
Similarly,
1
( ) ( ) ... . (
4
. )ar ar ADCF iD vR
Adding (iii) and (iv), we have
( [ar ar(
( [Area ..... (v)
1
( ) ( ) )]
4
1
( ) ( )]
)
)
4
ar ar ABC ADC
ar ar ABCD
BSP DRF
BSP DRF
Similarly,
( [ara ..... (vi)r
1
(
)
4
)) ( ]ar AASR P DF BC C
Adding eq. (v) and (vi),
( ar(
ar +a
[Area ..... ii)
r
(v
( ) ( )
1
( )]
2
) )
BSP DRF ASR PCFar
ABCD

Now, adding the Area (SPFR) on both the sides, we
get
( (
[ar +ar(PFRS)
ar(ABCD)
+a
[ar
r
+ar(PFRS)
[ar = ar(PFRS)
( ) ( )
1
( )
) ) ( )
]
2
1
( )]
2
1
( )]
2
BSP DRF ASR PCFar ar ar
ABCD
ABCD
AB
ar PFRS
CD
Hence, it is proved.
EXERCISE 9.4
Question: 1
A point E is taken on the side BC of a parallelogram
ABCD. AE and DC are produced to meet at F. Prove
that Area (∆ADF) = Area (ABFC).

Solution:
Diagonal of a parallelogram divides it into two
triangles of equal area.
∴Area (∆ABC) = Area (∆ACD)....... (i)
Also,
Area (∆ABC) = Area (∆ABF)………..... (ii)
(Triangles on the same base AB and between the
same parallels AB and CF are equal in area)
From (i) and (ii), we have
Area (∆ACD) = Area (∆ABF) ... (iii)
Now,
Area (∆ADF) = Area (∆ACF) + Area (∆ACD)
⇒Area (∆ADF) = Area (∆ACF) + Area (∆ABF) (From
(iii))
⇒Area (∆ADF) =Area (quadrilateral ABFC)
Hence, it is proved.

Question: 2
The diagonals of a parallelogram ABCD intersect at a
point O. Through O, a line is drawn to intersect AD at
P and BC at Q. Show that PQ divides the
parallelogram into two parts of equal area.
Solution:
In
APO
and
CQO
,
POA COQ
(Vertically opposite angles)
OA = OC (Diagonals of parallelogram bisect each
other)
OCQPAO
(Alternate interior angles)
So,
POA QOC
(By ASA Congruence Rule)
∴Area (∆POA) = Area (∆QOC)......... (i)
The diagonal AC of parallelogram ABCD divides it into
two triangles of equal area.
∴Area (∆ABC) = Area (∆ADC) …….. (ii)
On adding eq. (i) and (ii), we get
2×Area (∆POA) + Area (∆ABC) = 2×Area (∆COQ) +
Area (∆ADC)
⇒Area (∆ABC) +Area (∆POA) +Area (∆POA) = Area
(∆ADC) + Area (∆COQ) + Area (∆COQ)
⇒Area (∆ABC) + Area (∆POA) − Area (∆COQ)
= Area (∆ADC) + Area (∆COQ) − Area (∆POA)

⇒Area (quadrilateral ABQP) = Area (quadrilateral
DCQP)
Hence, it is proved.
Question: 3
The medians BE and CF of a triangle ABC intersect at
G. Prove that the area of ∆GBC= area of the
quadrilateral AFGE.

Solution:
We know that a median of a triangle divides it into
two triangles of equal area.
As CF is the median of ∆ABC,
Area Area Area ( ) (
1
) .
2
BCF ACF ABC i
Also,
BE is a median of ∆ABC,
Area Area Area ( )
1
2
ABE BCE ABC ii
From eq. (i) and (ii), we have
Area Area
Area Area
Area Area
Area Area
( )
ABE BCF
BFG AFGE
BFG BGC
AFGE BGC

Hence, it is proved.
Question: 4
In Fig. 9.24,
||CD AE
and
||CY BA
. Prove that
Area (∆CBX) = Area (∆AXY).
Solution:
It is given that
| .|CY BA
Now, triangles on the same base and between the
same parallels are equal in area.

∴ Area (∆AYC) = Area (∆BCY)
(As both are on the same base CY and between the
same parallel lines CY and BA)
Area Area
Area Area
Area Area
( ) ( )
( ) ( )
( ) ( )
AXY CXY
BXC CXY
AXY BXC
Hence, it is proved.
Question: 5
ABCD is a trapezium in which
| ,|AB DC
30DC cm
and
50AB cm
. If X and Y are, respectively the
mid-points of AD and BC, prove that
7
( ) ( )
9
ar DCYX ar XYBA
Solution:

It is given that ABCD is a trapezium with
| ,|AB DC
30DC cm
and
50AB cm
.
Let us join DY and produce it to meet AB produced at
M.
In ∆DCY and ∆YBM,
CYD BYM
(Vertically opposite angles)
CY = BY (Y is the midpoint of BC)
DCY MBY
(Alternate opposite angles)
Thus
CYD BYM
(By ASA congruence rule)
So, DY = YM and DC = BM=30cm (By CPCT)
Now, in ∆DAM,
X and Y is the midpoints of AD and DM.
∴Using the midpoint theorem,
||XY AM
and
cm.
1 1 1 1
( ) (50 30) 80 40
2 2 2 2
XY AM AB BM
It is given that X and Y are, respectively the
mid-points of AD and BC.

∴Trapezium DCYX and ABYX are of same height, say h
cm.
Now,
Area of a trapezium
=
1
2
(Sum of parallel sides)×(Distance between them)
So, Area of trapezium DCYX =
1
2
(30+40)
×
h
=
1
2
×
70 h
Similarly, Area of trapezium ABYX =
1
2
(50+40)
×
h

=
1
2
×
90 h
Thus,
70 7
( ) 90 9
7
( )
9
h
ar
ar DCYX
ar D
ABYX h
ar ABYXCYX
Hence, it is proved.
Question: 6
In ∆ABC, L and Mare the points on AB and AC,
respectively such that
||LM BC
. Prove that
Area (LOB) = Area (MOC).

Solution:
It is given that
||LM BC
.
So, ∆BCL and ∆CBM are on the same base BC and
between the same parallel lines LM and BC).
Therefore,
ar ar
ar ar ar ar
ar ar
( ) ( )
(( ) ( ) ( ) )
( ) ( )
BCL CBM
LOB BOC MOC BOC
LOB MOC
Hence, it is proved.

Question: 7
In Fig. 9.25, ABCDE is any pentagon. BP drawn
parallel to AC meets DC produced at P and EQ drawn
parallel to AD meets CD produced at Q. Prove that
Area (ABCDE) = Area (APQ)
Fig. 9.25
Solution:
It is given that
BP AC
and
EQ AD
.
Now,
∆ABC and ∆APC lie on the same base AC and
between the same parallel lines AC and BP.
So, Area (∆ABC) = Area (∆APC) …. (i)
Similarly,
∆ADE and ∆ADQ lie on the same base AD and
between the same parallel lines AD and EQ.
So, Area (∆ADE) = Area (∆ADQ) …. (ii)
Now, Area (ABCDE) = Area (∆ABC) + Area (∆ACD) +
Area (∆ADE)
⇒Area (ABCDE) = Area (∆APC) + Area (∆ACD)
+Area (∆ADQ) (From (i) and (ii))

⇒Area (ABCDE) = Area (∆APQ)
Hence, it is proved.
Question: 8
If the medians of a ∆ABC intersect at G, show that
Area (AGB) = Area (AGC) = Area (BGC) =
1
3
Area (ABC)
Solution:
Let say AD, BE and CF are the medians of the given
triangle ABC.
It is given that the medians of ∆ABC intersect at G.
We know that, the median of a triangle divides it into
two triangles of equal area.
In ∆ABC, BE is the median.
Area (∆ABE) = Area (∆BEC)……….... (i)
In ∆GAC, GE is the median.
Area (∆GAE) = Area (∆GCE)……...... (ii)
Subtracting (ii) from (i), we get
Area (∆ABE) - Area (∆GAE) = Area (∆BEC) - Area
(∆GCE)
Area (∆AGB) = Area (∆BGC)……..… (iii)
Similarly, Area (∆AGB) = Area (∆AGC)……..... (iv)
From (iii) and (iv), we get
Area (∆AGB) = Area (∆BGC) = Area (∆AGC)…. (v)

Now, Area (∆AGB) + Area (∆BGC) + Area (∆AGC) =
Area (∆ABC)
⇒Area (∆AGB) + Area (∆AGB) + Area (∆AGB) = Area
(
∆
ABC) (Using (v))
⇒3Area (∆AGB) = Area (∆ABC)
⇒Area (∆AGB) =
1
3
Area (∆ABC)……….... (vi)
From (v) and (vi), we get

Area (∆AGB) = Area (∆BGC) =Area (∆AGC) =
1
3
Area (∆ABC)
Hence, it is proved.
Question: 9
In Fig. 9.26, X and Y are the mid-points of AC and AB
respectively, QP || BC and CYQ and BXP are straight
lines. Prove that Area (ABP)=Area(ACQ).
Fig. 9.26
Solution:
Let us join QB and PC.

It is given that X and Y are the mid-points of AC and
AB respectively.
Therefore, in ∆ABC,
XY BC
and
1
2
XY BC
….. (i)(Midpoint theorem)
Now, in ∆ABP, Y is midpoint of AB and
( ),
1
.
2
XY AP XY BC QP
XY AP ii
(By using the midpoint theorem)
From (i) and (ii),
AP= BC
Also,
AP BC
(∵
BC QP
is given)
Hence, quadrilateral ABCP is a parallelogram.
Now, BP is a diagonal of parallelogram ABCP and
diagonal of a parallelogram divides it into two
triangles of equal area.
So, Area (∆ABP) = Area (∆BPC) …. (iii)
Similarly, we can show that quadrilateral QBCA is
parallelogram and hence,
Area (∆AQC) = Area (∆QBC) …. (iv) [As QC is the
diagonal]
Now, Area (∆QBC) = Area (∆BPC)… (v)
(∵Both the triangles lie on the same base BC and
between the same parallel lines QP and BC)
From (iii), (iv) and (v), we have
Area (∆ABP) = Area (∆ACQ)

Hence, it is proved.
Question: 10
In Fig. 9.27, ABCD and AEFD are two parallelograms.
Prove that
Area (PEA) = Area (QFD) [Hint: Join PD].
Solution:
It is given that ABCD is a parallelogram.
So,
.AB CD AP DQ
Also, AEFD is a parallelogram.
AD EF AD EQ AD PQ
Now, in quadrilateral APQD,
and ADAP DQ PQ
So, APQD is a parallelogram.
Now, APQD and AEFD are two parallelograms that lie
on the same base AD and between the same parallel
lines AD and EQ.
So, Area (∥gm APQD) = Area (∥gm AEFD)
⇒Area (∆FQD) + Area (Trapezium APFD) = Area
(∆PEA) + Area (Trapezium APFD)
⇒Area (∆FQD) =Area (∆PEA)
Hence, it is proved.