Lesson: Circles
Exercise 10.1 (10 Multiple Choice Questions and
Answers)
Question: 1
AD is a diameter of a circle and
AB
is a chord. If
34 cm, 30 cmAD AB
, the distance of
AB
from
the centre of the circle is:
(a) 17 cm
(b) 15 cm
(c) 4 cm
(d) 8 cm
Solution:
d
Given,
34 cm, 30 cm,AD AB
Let us draw the figure.

Now,
diameter
cm
34
17
2 2 2
AD
OA
and
1
2
AM AB
(
Perpendicular from the center of circle to the
chord bisects it)
Now, in right
AMO
,
(
2 2 2
) ( ) ( )OM OA AM
(By Pythagoras theorem)
cm
2 2
(17) (15)
289 225
64
64
8
OM
Hence, the distance of
AB
from the center of circle is
8 cm.
Question: 2
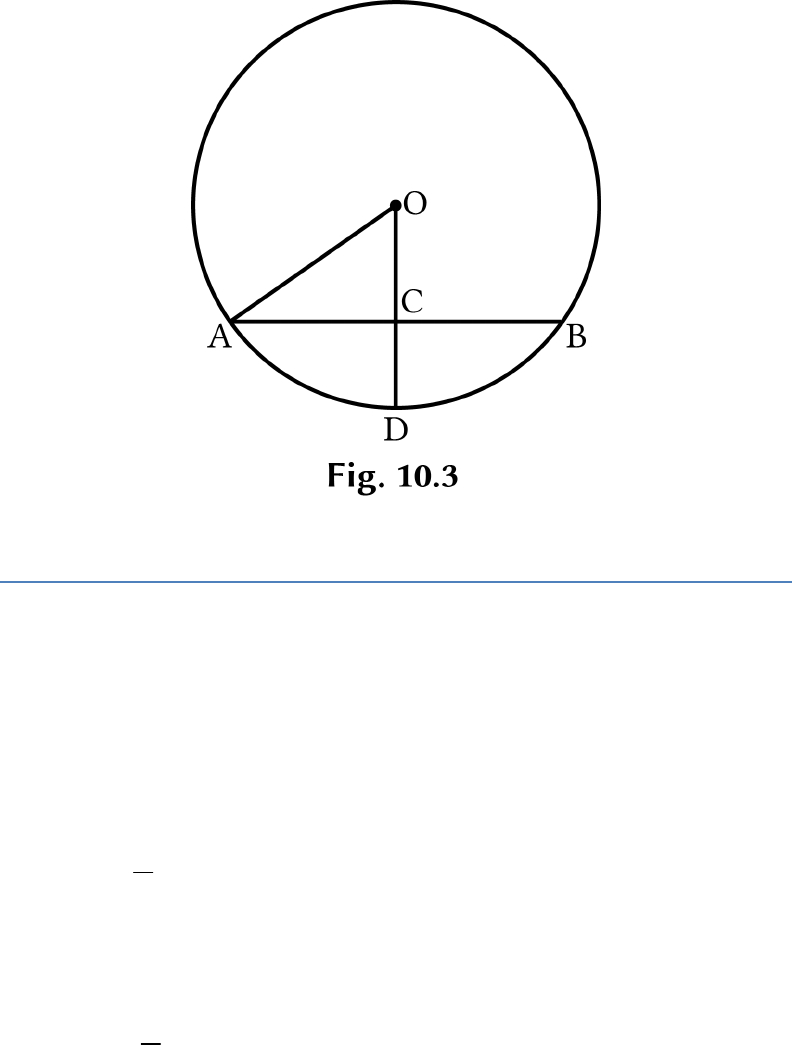
In Fig. 10.3, if
5 cm, 8 cmOA AB
and
OD
is
perpendicular to
AB
, then CD is equal to:
a cm
cm
c cm
d cm
b
2
3
4
5
Solution:
a
Given,
cm cm5 , 8OA AB
and
OD AB
,
Let us draw a figure,
OD AB
1
2
AC AB
(
Perpendicular from the centre of
circle to the chord bisects it)
cm
1
8
2
4
AC
AC
Now in right
ACO
,
(
2 2 2
) ( ) ( )OC OA AC
(By Pythagoras theorem)

cm
2 2
(5) (4)
25 16
9
9
3
OC
Then,
cm
5 3
2
CD OD OC
Question: 3
If
12 cm, 16 cmAB BC
and
AB
is perpendicular to
BC
, then the radius of the circle passing through the
points
A
,
B
and
C
is:
(a) 6 cm
(b) 8 cm
(c) 10 cm
(d) 12 cm
Solution:
c
Given,
12 cm, 16 cmAB BC
and
AB BC
,

AB BC
AC
is diameter
Now, in right
CBA
,
2
2 2
( ) ( )AC AB BC
(By Pythagoras theorem)
2 2
(12) (16)
144 256
=400
400AC
= 20 cm
Then, radius
2
AC
cm
20
10
2
Hence, required radius is 10 cm.

Question: 4
In Fig.10.4, if
20ABC
, then
AOC
is equal to:
(a) 20°
(b) 40°
(c) 60°
(d) 10°

Solution:
b
Given,
20ABC
,
Now,
2AOC ABC
(
By inscribed angle
1
2
central
angle)
2
2 20
40
AOC ABC
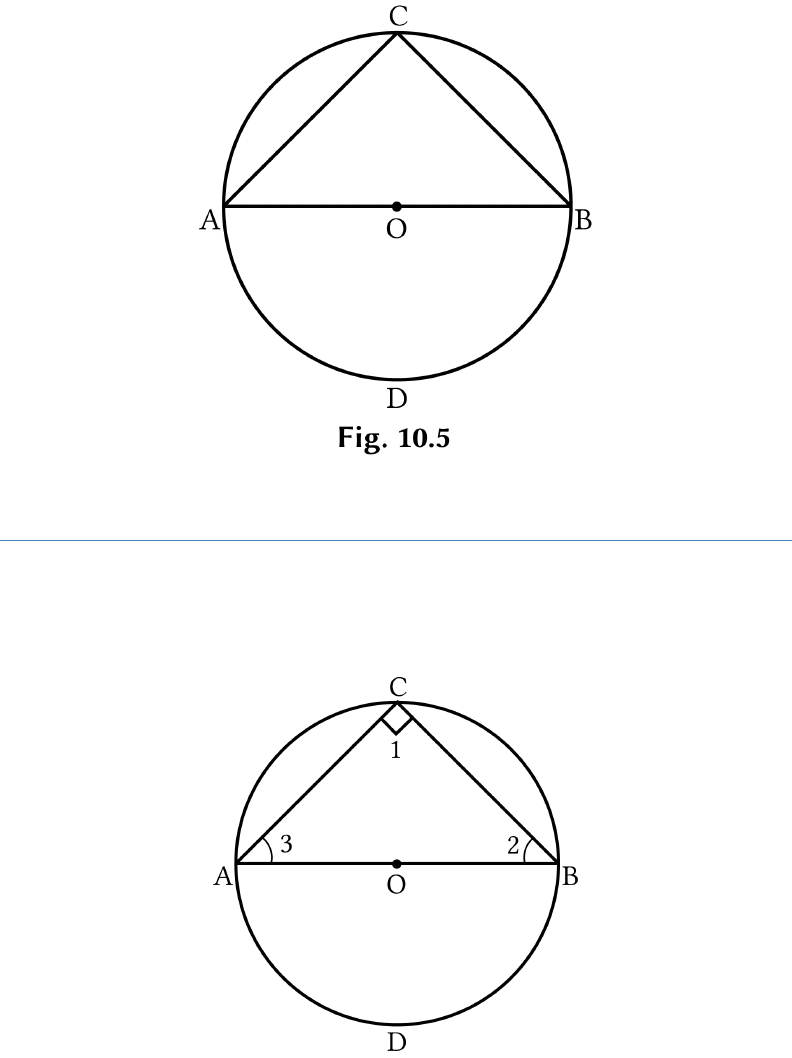
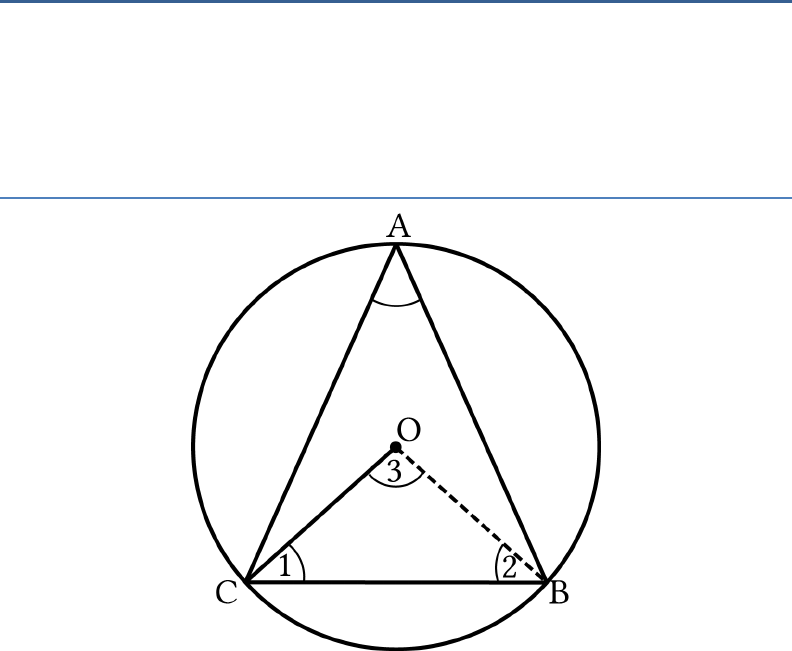
Question: 5
In Fig.10.5, if
AOB
is a diameter of the circle
and
AC BC
, then
CAB
is equal to:
(a) 30°
(b) 60°
(c) 90°
(d) 45°
Solution:
d
Given,
AC BC
and
AOB
is a diameter,
1 90
(Angle in semicircle)
In right
,ACB AC BC
(Given)
2 3
(By triangle isosceles property)
Now,
1 2 3 180
(By Angle sum property of a
triangle)

[ ]90 3 3 180 1 90 , 2 3
2 3 180 90
2 3 90
45CAB
Question: 6
In Fig. 10.6, if
40OAB
, then
ACB
is equal to:
(a) 50°
(b) 40°
(c) 60°
(d) 70°
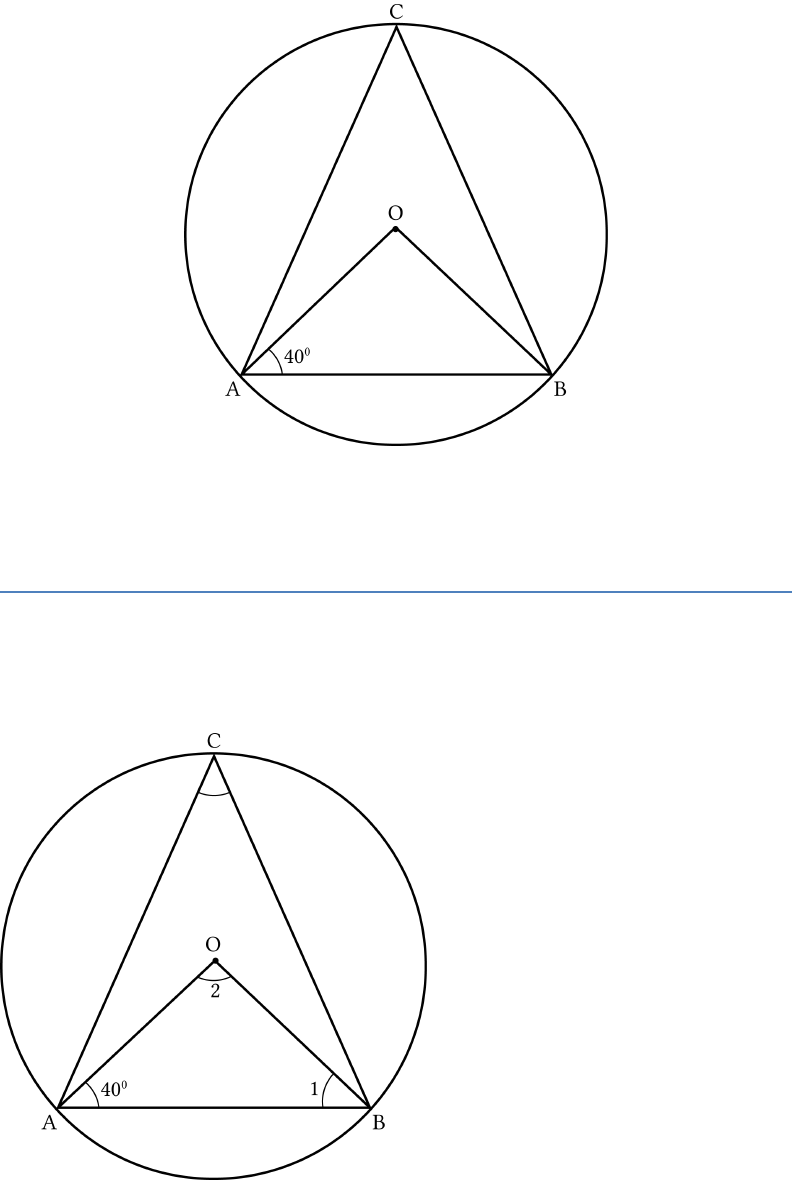
Fig. 10.6
Solution:
a
Given,
40OAB
,
In
,AOB OA OB
(
Both are radius of the given
circle)
1 40OAB
(By triangle isosceles
property)
Now,

1 2 180OAB
(By Angle sum property of
)
40 2 40 180
2 180 80
2 100
Then,
1
2
ACB AOB
(
By inscribed angle
1
2
central
angle)
1
100
2
50
Question: 7
In Fig. 10.7, if
60 , 50 DAB ABD
, then
ACB
is equal to:
(a) 60°
(b) 50°

(c) 70°
(d) 80°
Solution:
c
Given,
60DAB
,
50ABD
In
ADB
180ADB DAB DBA
(By Angle sum
property of a
triangle
)

60 50 180
180 110
70
ADB
ADB
ADB
Therefore,
70ACB ADB
(As angles on the
same segment are equal)
Question: 8
ABCD is a cyclic quadrilateral such that AB is a
diameter of the circle circumscribing it and
140 ADC
, then
BAC
is equal to:
(a) 80°
(b) 50°
(c) 40°
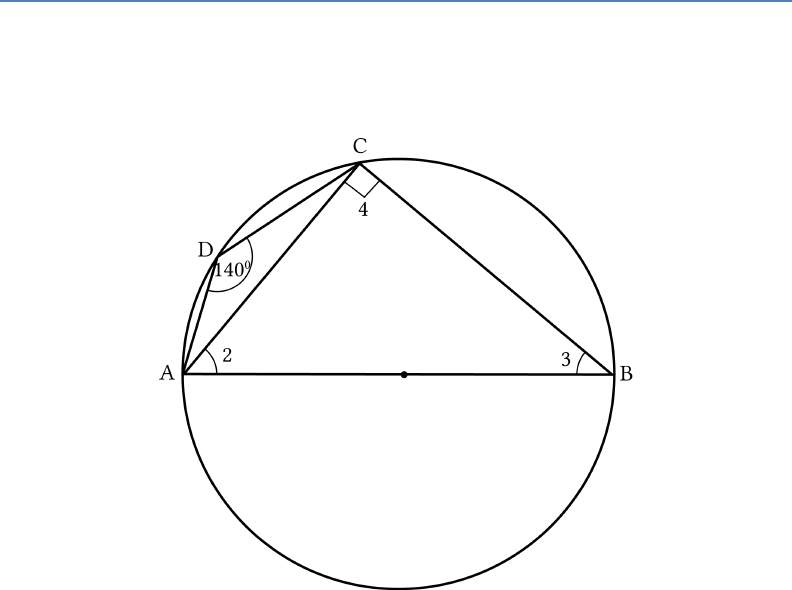
(d) 30°
Solution:
b
Given,
140 , ADC
4 90
(Angle in semicircle)
3 180 ADC
(
Opposite angles of cyclic
quadrilateral)
140 3 180
3 180 140
3 40
Now,
In
,ACB

4 3 2 180
90 40 2 180
2 180 130
2 50
Hence,
2 50BAC
Question: 9
In Fig. 10.8,
BC
is a diameter of a circle and
60BAO
. Then
ADC
is equal to
(a) 30°
(b) 45°
(c) 60°

(d) 120°
Solution:
c
Given,
60 BAO
and
BC
is a diameter of a circle.

In
,BAO OA OB
(
Both are radius of the given
circle)
1 60OAB
(By triangle isosceles
property)
2 1 OAB
(By exterior angle property of ∆)
60 60
120
Now,
2 2 3
(
The angle at the centre is twice the
angle at the circumference)
120 2 3
3 60
Therefore,
60ADC
Question 10
In Fig. 10.9,
90AOB
and
30ABC
, then
CAO
is equal to:
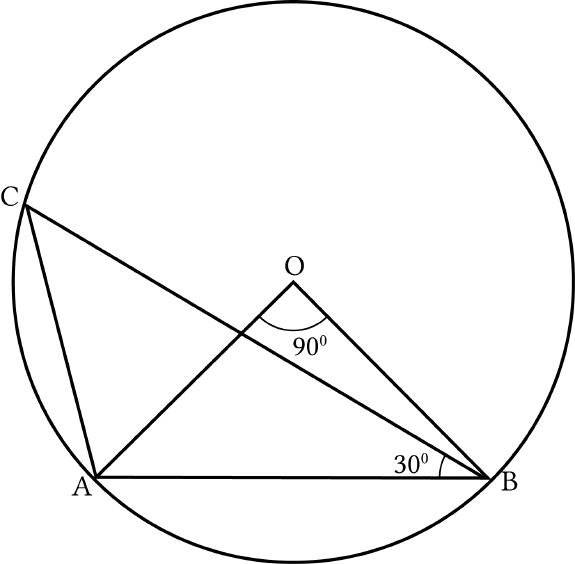
Fig 10.9
(a) 30°
(b) 45°
(c) 90°

(d) 60°
Solution:
d
Given,
90AOB
and
30ABC
In the above figure,
2AOB ACB
(
The angle at the centre is twice
the angle at the circumference)
90 2
45
ACB
ACB
In
,ACB
180ACB CAB ABC
(By Angle sum
property of
)
45
30 180
180 75
105
CAB
CAB
Now, in
,AOB OA OB
(
Both are radius of the
given circle)
... )OAB OBA (i
(By triangle isosceles
property)

(By ( ))
2
180
90 2 180
180 90 90
90
45
2
AOB OAB OBA
OAB i
OAB
OAB
Now,
105 45
60
CAO CAB OAB
Exercise 10.2
Write True or False and justify your answer in each
of the following:
Question 1
Two chords
AB
and
CD
of a circle are each at
distances 4 cm from the centre. Then
AB CD
Solution:
True

In
and ,OEB OFD
cm4OE OF
(Given)
OB OD
(
Both are radius of the circle)
And
OEB OFD
(
Each 90°)
OEB OFD
(
By RHS congruence rule
)
BE DF
(By CPCT)
2 2BE DF
(By multiplying 2 on both the sides)
AB CD
(
The perpendicular from the centre of
a circle to a chord bisects the chord
)
Question 2
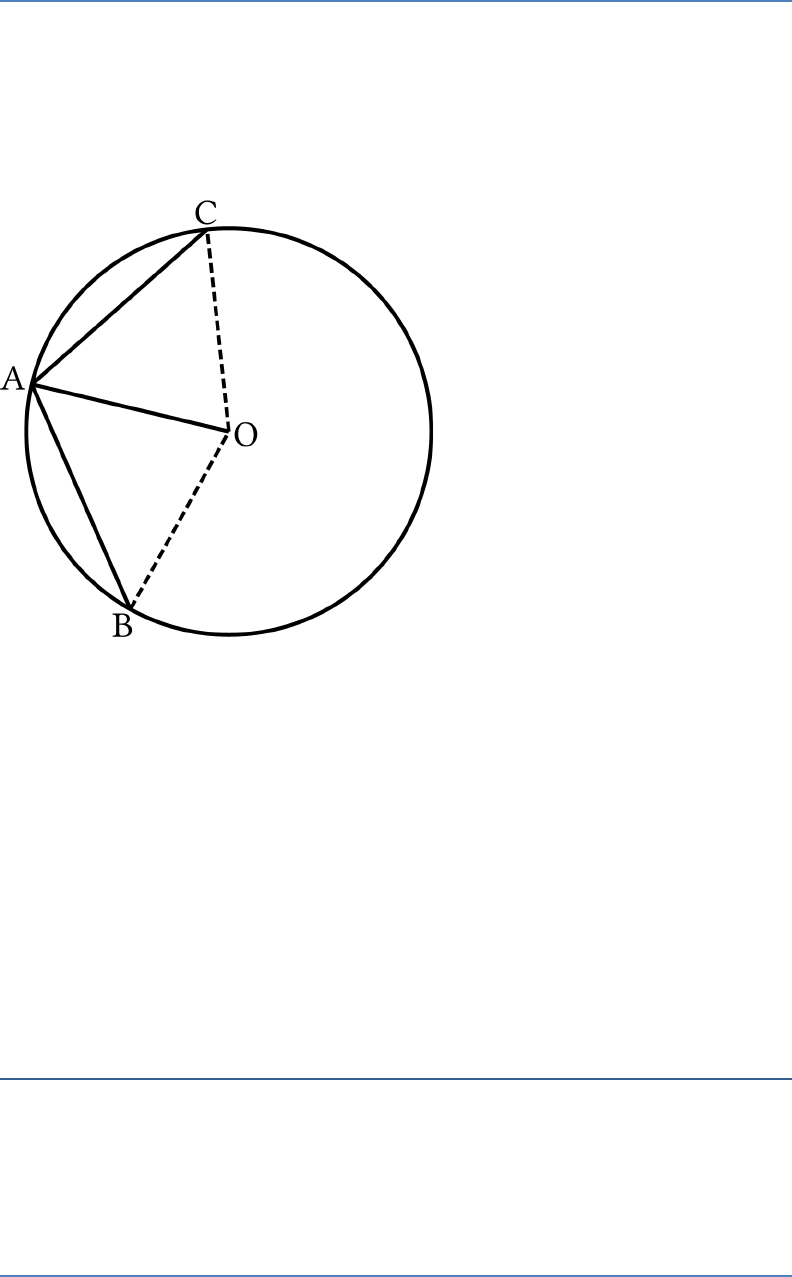
Two chords
AB
and
AC
of a circle with centre
O
are
on the opposite sides of
OA
. Then
OAB OAC
Solution:
False
Given:
AB
and
AC
are two chords of a circle.
Joining
OB
and
OC
,
In
and ,AOB AOC
OC OB
(
Both are radius of the circle)
OA OA
(Common)
Here,
OAB OAC
if
AOB AOC
or if
AB AC
Question 3
The congruent circles with centres
O
and
O
intersect
at two points
A
and
B.
Then
AOB AO B
.
Solution:
True,

Because equal chords of congruent circles subtend
equal angles at the respective centres.
Question 4
Through three collinear points, a circle can be drawn.
Solution:
False,
A circle can pass through two collinear points but
not through three collinear points.
Question 5
A circle of radius 3 cm can be drawn through two
points
A
,
B
such that
cm6AB
.
Solution:
True
If AB is diameter, then the radius
diameter
2
cm
cm
2
6
2
3
AB
Question 6
If
AOB
is a diameter of a circle and
C
is a point on
the circle, then
2 2 2
AC BC AB
.
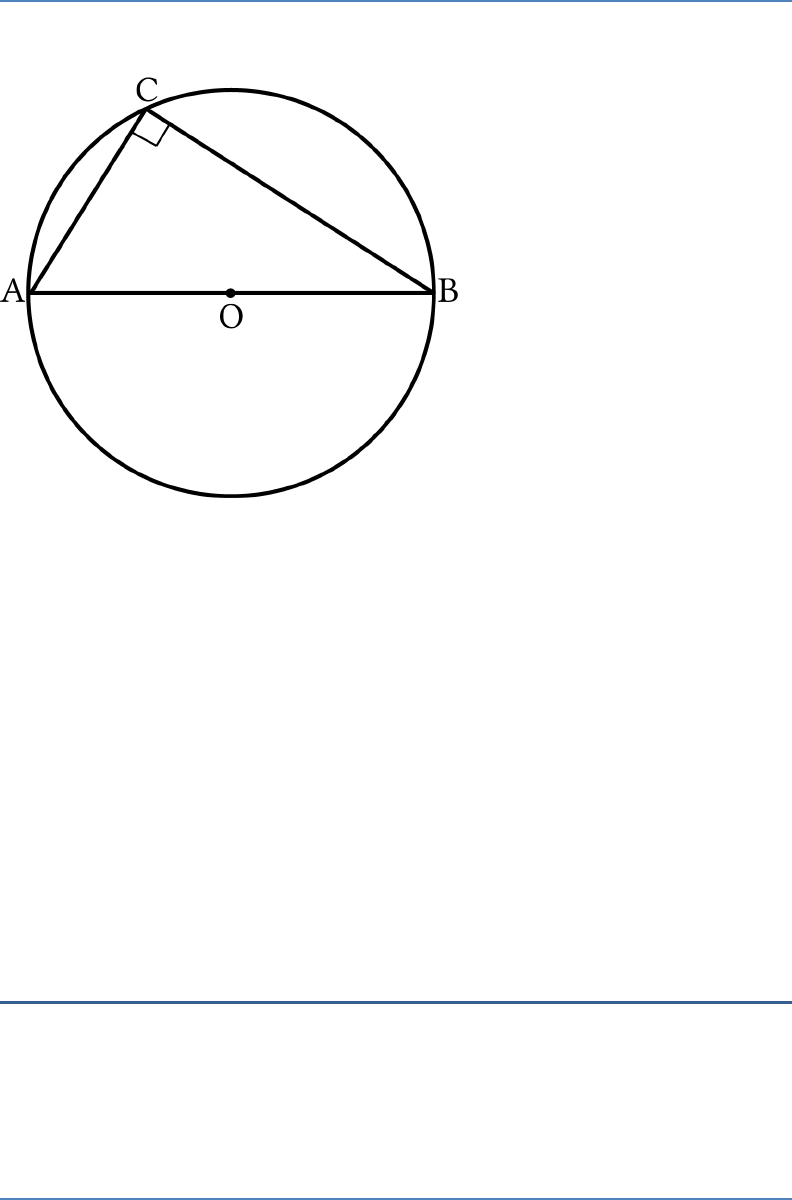
Solution:
True
90ACB
(
Angle in a semicircle is a right angle
)
In right
ACB
,
2 2 2
AC BC AB
(
By Pythagoras theorem
)
Question 7
ABCD
is a cyclic quadrilateral such that
and 90 , 70 , 95 105A B C D
Solution:
False
In a cyclic quadrilateral,
A C
180B D
But,

175 18070 105 B D
∴
ABCD
is not a cyclic quadrilateral.
Question 8
If
A
,
B
,
C
,
D
are four points such
that
and 30 60BAC BDC
, then
D
is the
centre of the circle through
A
,
B
and
C
.
Solution:
True
We know, that angle subtended by an arc at the
centre of the circle is double that of the angle
subtended by the same arc at the circumference.
So,
BDC
can be considered as angle at centre and
BAC
as the angle at circumference. Thus
D
is the
centre of the circle through
A
,
B
and
C
.
Question 9
If
A
,
B
,
C
and
D
are four points such that
45 BAC
and
45 BDC
, then
A
,
B
,
C
,
D
are
concyclic.
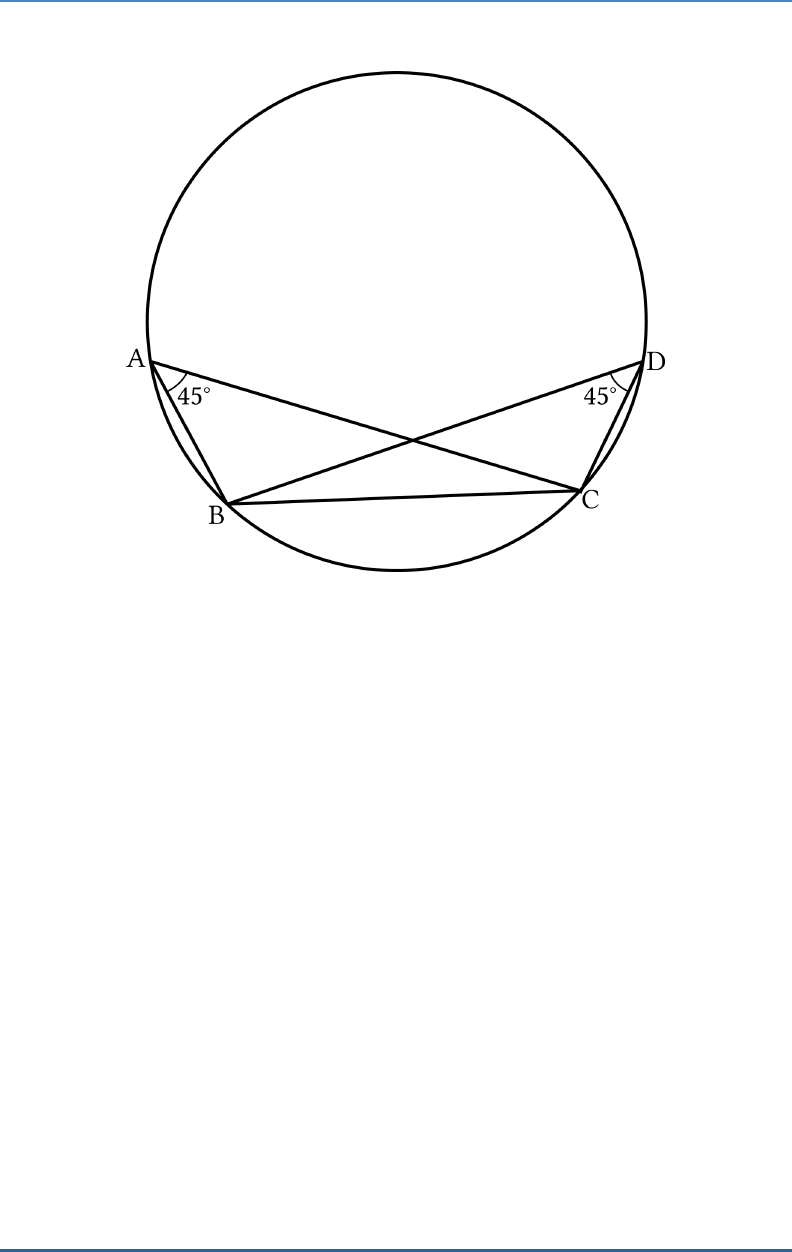
Solution:
True
As angles in the same segment are equal, therefore
A
,
B
,
C
,
D
are concyclic.
Question10
In Fig. 10.10, if
AOB
is a diameter and
120ADC
,
then
30CAB
.

Solution:
True
Let us join
AC
.
90 ACB
… (i)
(
Angle in the semi-circle is a right
angle
)
Since
ABCD
is cyclic,
180 ABC ADC
120 180 ABC
(
Opposite angle of cyclic
)
...( )
180 120
60 ii
ABC
ABC
Now, in
ABC
,
Using angle sum property we have,
(Using (i) and (ii))
180
60 90 180
180 150
30
CAB ABC ACB
CAB
CAB
CAB
Exercise 10.3
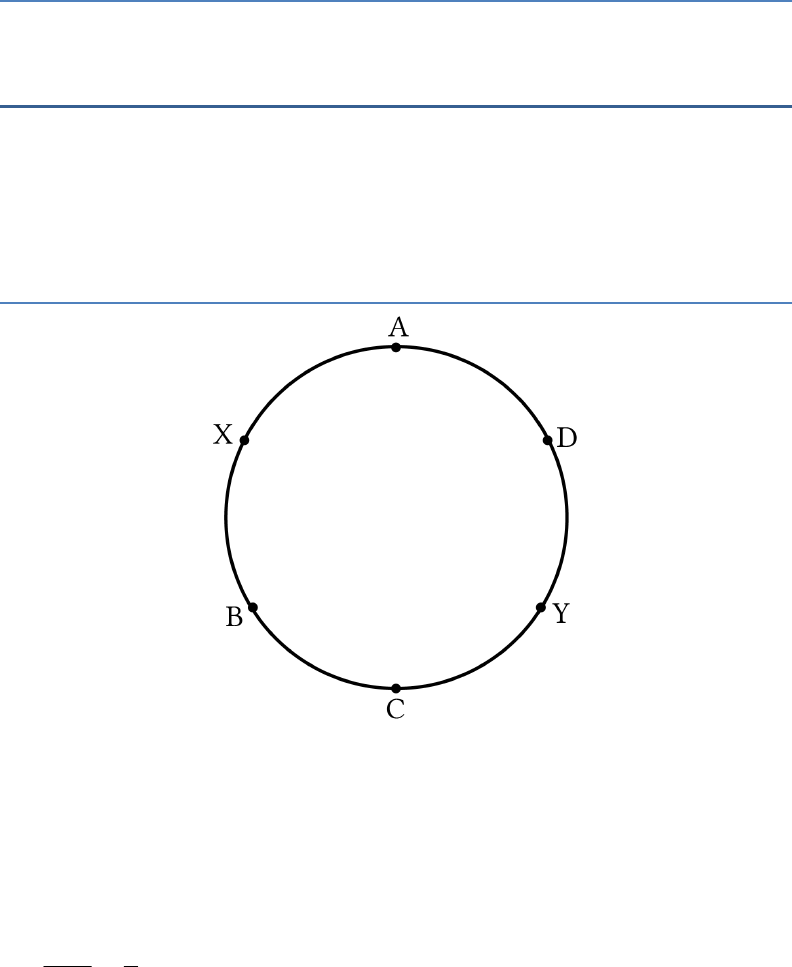
Question: 1
If arcs
AXB
and
CYD
of a circle are congruent, find
the ratio of
AB
and
CD
.
Solution:
Given,
arc arcAXB CYD
AB CD
(Equal arcs have equal corresponding
chords.)
1
1
AB
CD
: 1:1. AB CD
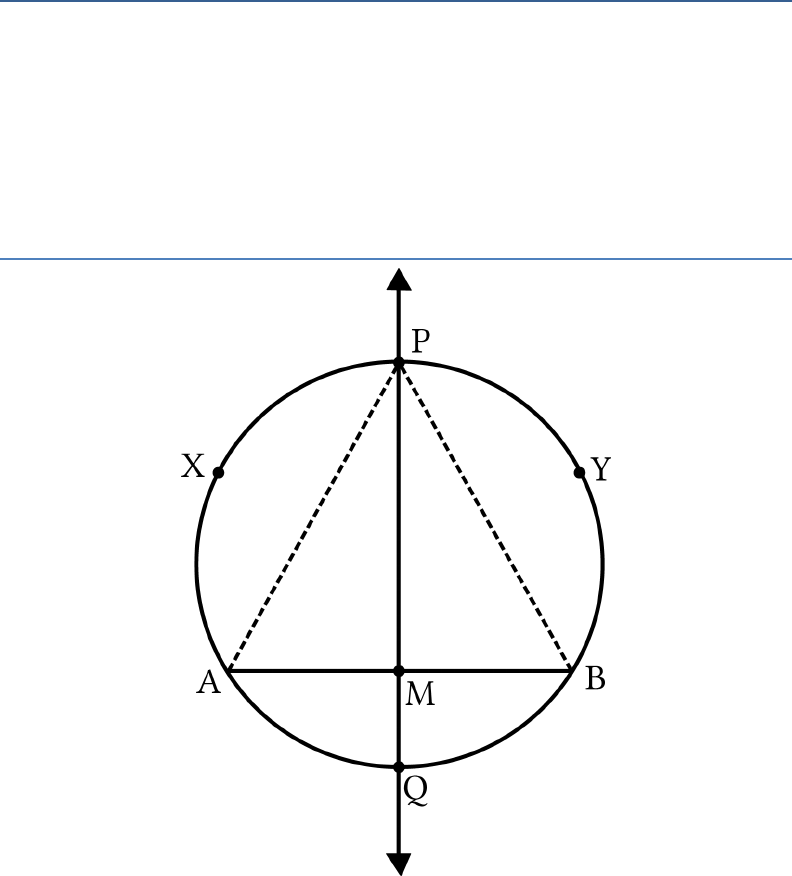
Question: 2
If the perpendicular bisector of a chord
AB
of a circle
PXAQB
Y intersects the circle at
P
and
Q
, prove that
arc
arcPXA PYB
.
Solution:
Let
AB
be a chord of the circle
PXAQB
Y and
PQ
be
the perpendicular bisector of the chord
AB
, which
intersect it at
M.
In
APM
and
BPM
,
PM PM
(Common side)
PMA PMB
(
PM AB
)
AM MB
(
PM
bisects
AB
)
Therefore,
APM BPM
(By SAS congruence
rule)
PA PB
(By CPCT)
arc arc PXA PYB
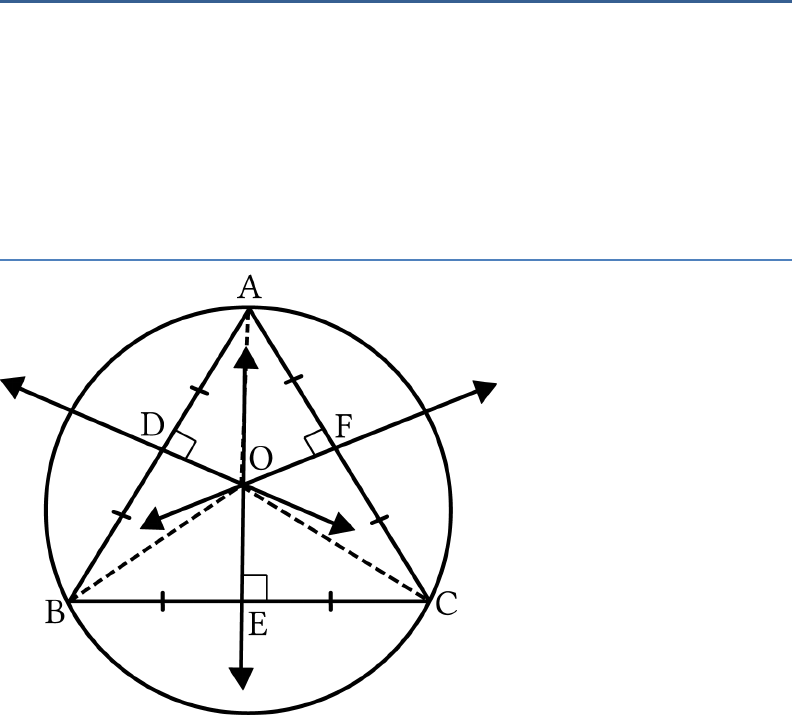
Question: 3
A
,
B
and
C
are three points on a circle. Prove that the
perpendicular bisectors of
AB
,
BC
and
CA
are
concurrent.
Solution:
Consider the perpendicular bisectors OD and OF of
lines AB and AC intersecting at the point O.
Now, draw perpendicular OE from the point O to the
line BC.
We need to show that
BE EC
In
AOD
and
BOD
,
AD BD
(OD is perpendicular bisector of AB)
ADO BDO
(Each
90
)
OD OD
(
Common)
Therefore,
AOD BOD
(By SAS congruence
rule)
OA OB
(By CPCT)
Similarly,
OFA OFC
(By SAS congruence rule)
OA OC
(By CPCT)
say( )OA OB OC r
Now, in
OEB
and
OEC
,
OB OC
(Proved above)
OE OE
(Common side)
And,
OEB OEC
(Each
90
)
Therefore,
OEB OEC
(By RHS congruence rule)
BE EC
(By CPCT)
Hence,
OE
is the perpendicular bisector of
BC
.
Hence, the perpendicular bisectors of
AB
,
BC
and
CA
are concurrent.

Question: 4
AB
and
AC
are two equal chords of a circle. Prove
that the bisector of the angle
BAC
passes through
the centre of the circle.
Solution:
Let us draw bisector of
BAC
and join
BC
and let
the intersecting point is
D
.
In
BAD
and
CAD
AB AC
(Given)
1 2
(AD is the bisector of
BAC
)
AD AD
(Common)
Therefore,
BAD CAD
(By SAS congruence
rule)
BD CD
(By CPCT)
And
BDA CDA
(By CPCT)
But,

180 BDA CDA
(Linear pair axiom)
180
2 180
90
90
BDA BDA
BDA
BDA
BDA CDA
Also,
BD CD
(As proved above)
So,
AD
is the perpendicular bisector of the
chord
.BC
Hence, bisector of
BAC
(
i.e.
AD
)
passes through
the centre
O
.
Question: 5
If a line segment joining mid-points of two chords of
a circle passes through the centre of the circle, prove
that the two chords are parallel.
Solution:
Let
P
and
Q
are the midpoints of two chords
AB
and
CD
respectively and the line segment joining
PQ
passes through centre.
Now, we need to prove that
AB CD
.

Since
P
is the midpoint of
AB
,
Therefore,
OP AB
.
(Since the line joining the centre of a circle to the
midpoint a chord is perpendicular to the chord)
90 ...( )APO i
Similarly,
OQ CD
...( )90OQD ii
From eq. (
i
) and (
ii
),
90 APO OQD
Thus, alternate interior angles are equal.
So,
AB CD
Question: 6
ABCD
is such a quadrilateral that
A
is the centre of
the circle passing through
B
,
C
and
D
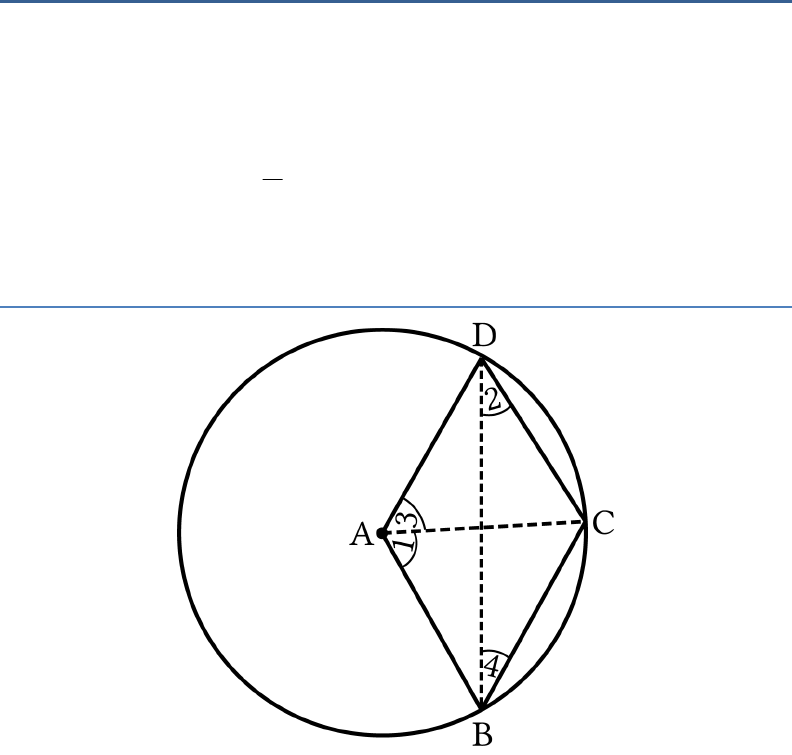
. Prove that
1
2
CBD CDB BAD
Solution:
In a circle,
...( )1 2 2 i
(The angle subtended by an arc at
the centre is twice the angle subtended by it in the
remaining part of the circle.)
Similarly,
...( )3 2 4 ii
(The angle subtended by an arc at
the centre is twice the angle subtended by it in the
remaining part of the circle.)
On adding eq. (
i
) and (
ii
), we get

1 3 2 2 2 4
2 2 4
2 2 4
1
2
BAD
BAD
CDB CBD BAD
Question: 7
O
is the circumcenter of the triangle
ABC
and
D
is
the mid-point of the base
BC
. Prove that
BOD A
.
Solution:
Let us join OB, OC and OD.
In
BOD
and
COD
,
OD OD
(Common side)
BD DC
(D is the midpoint of BC)
OB OC
(Both are radius of circle)
Therefore,
BOD COD
(By SSS congruence
rule)

BOD COD
(By CPCT)
(i)
1
...
2
BOD COD BOC
In a circle, the angle subtended by an arc at the
centre is twice the angle subtended by it in the
remaining part of the circle.
2 BAC BOC
1
2
BAC BOC
BAC BOD
(Using (i))
( )A BOD BAC A
Question: 8
On a common hypotenuse
AB
, two right triangles
ACB
and
ADB
are situated on opposite sides. Prove
that
BAC BDC
.
Solution:
Let us join
CD.

90 90 180 C D
ADBC
is a cyclic quadrilateral.
BAC BDC
(Angles in the same segment
BC
of a circle are equal.)
Question: 9
Two chords
AB
and
AC
of a circle subtend angles
equal to 90° and 150°, respectively at the centre.
Find
BAC
, if
AB
and
AC
lie on the opposite sides
of the centre.
Solution:
In
Δ , AOB OA OB
(Both are radius of the circle.)
2 1
(Angles opposite to equal sides are equal.)
1 2 3 180
(By angle sum property of
Δ
)
2 2 90° 180° ( 2 1)
2 45°
In
Δ , AOC OA OC
(Both are radius of the circle.)
5 4
(Angles opposite to equal sides are equal.)
4 5 180AOC
(By angle sum property of
Δ
)
4 4 150 180 ( 5 4)
4 15
2 4
45 15
60
BAC

Question: 10
If
BM
and
CN
are the perpendiculars drawn on the
sides
AC
and
AB
of the triangle
ABC
, prove that the
points
B
,
C
, M and
N
are concyclic.
Solution:
We need to prove that
B, C, M, N
are concyclic.
Let us suppose BC is a diameter of the circle.
Then,
BC
subtends
1
and
2
on the same side and
Each1 2 90
So, points
M
and
N
lie on circle.
∴
Points
B, C, M, N
are concyclic.
Question: 11
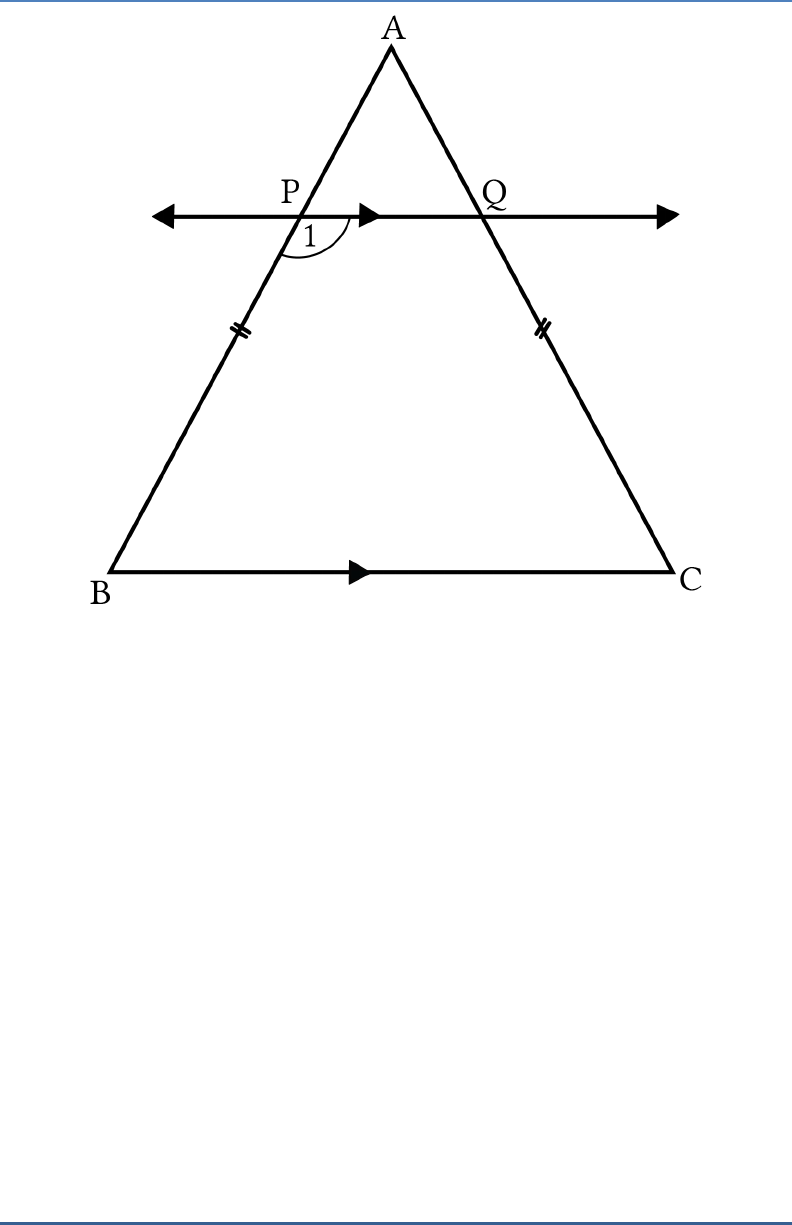
If a line is drawn parallel to the base of an isosceles
triangle to intersect its equal sides, prove that the
quadrilateral so formed is cyclic.
Solution:
Given,
PBCQ
is cyclic
Now, in
ΔABC
AB AC
(Given)
C B
(Isosceles
property)
1 180
1 180
PQ BC
B
C B C
PBCQ
is cyclic
Question: 12
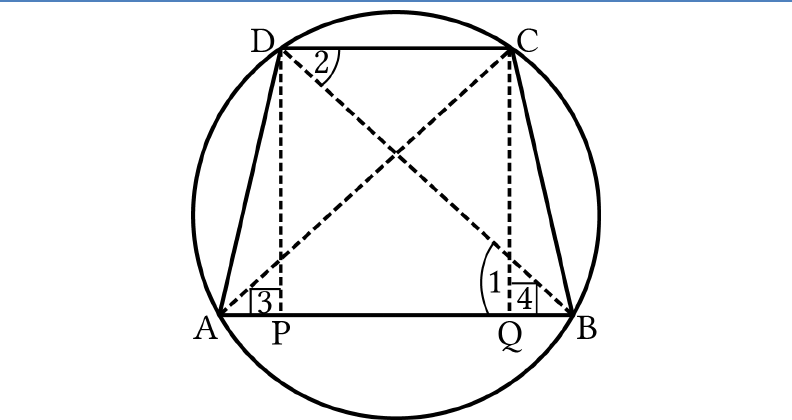
If a pair of opposite sides of a cyclic quadrilateral is
equal, prove that its diagonals are also equal.
Solution:
Let us suppose
ABCD
is a cyclic quadrilateral in
which
AD BC
.
We need to prove that
AC BD
.
Let us join
AC
and
BD
and draw
,DP AB CQ AB
Since
AD BC
,
arc arc AD BC
1 2
(Equal chords of a circle subtends equal
angles at the centre and also, the angle subtended by
a chord at the centre is twice the angle subtended by
it at the remaining part of the circle)
But these are alternate interior angles.
DC AB
DP CQ
…(i) (Distance between parallel lines)
Now, in
DAP
and
CBQ
3 4
(Each
90
)
DP CQ
(Using (i))
AD BC
(Given)
DAP CBQ
(By R.H.S. property)
A B
(CPCT)
In
DAB
and
CBA
,
DA CB
(Given)
A B
(Proved above)
AB BA
(Common)
DAB CBA
by SAS property
BD AC
Question: 13
The circumcenter of the triangle
ABC
is
O
. Prove
that
90 OBC BAC
.
Solution:
In
OBC
,
OB OC
(Radii of a triangle)

2 1
(Isosceles triangle property)
Now,
1 2 3 180
(Angle sum property of
triangle)
2 1 3 180 1 2
But
3 2 A
2 1 2 180 A
1 90A
90OBC BAC
Question: 14
A chord of a circle is equal to its radius. Find the
angle subtended by this chord at a point in major
segment.
Solution:
Let
AB
is the chord of a circle with centre
O
such
that
AB OA OB
We need to find
D
in the figure.

Now, in
OAB
,
OA OB AB
(Given)
∴
OAB
is an equilateral triangle
.
Hence,
60 AOB
(Each angle of equilateral triangle)
But,
2AOB D
60
2
30
D
D
Question: 15
In Fig. 10. 13,
130ADC
and chord
BC
chord
BE
. Find
CBE
.

Solution:
Let
M
be the centre of the circle.
Let us join
CM
,
EM
and
CE
.
ADCB
is cyclic

1 180
1 130 180
1 180 130
1 50
ADC
Now,
CM EM
(Radius of a circle) and
BC BE
(Given)
BCME
is a kite
MB CE
(Diagonals of a kite are perpendicular
to each other)
BCE
is an isosceles triangle (
BC BE
)
And
BO CE
Thus,
BO
bisects
CBE
2 1 50
Now,
1 2
50 50
100
CBE
CBE
CBE
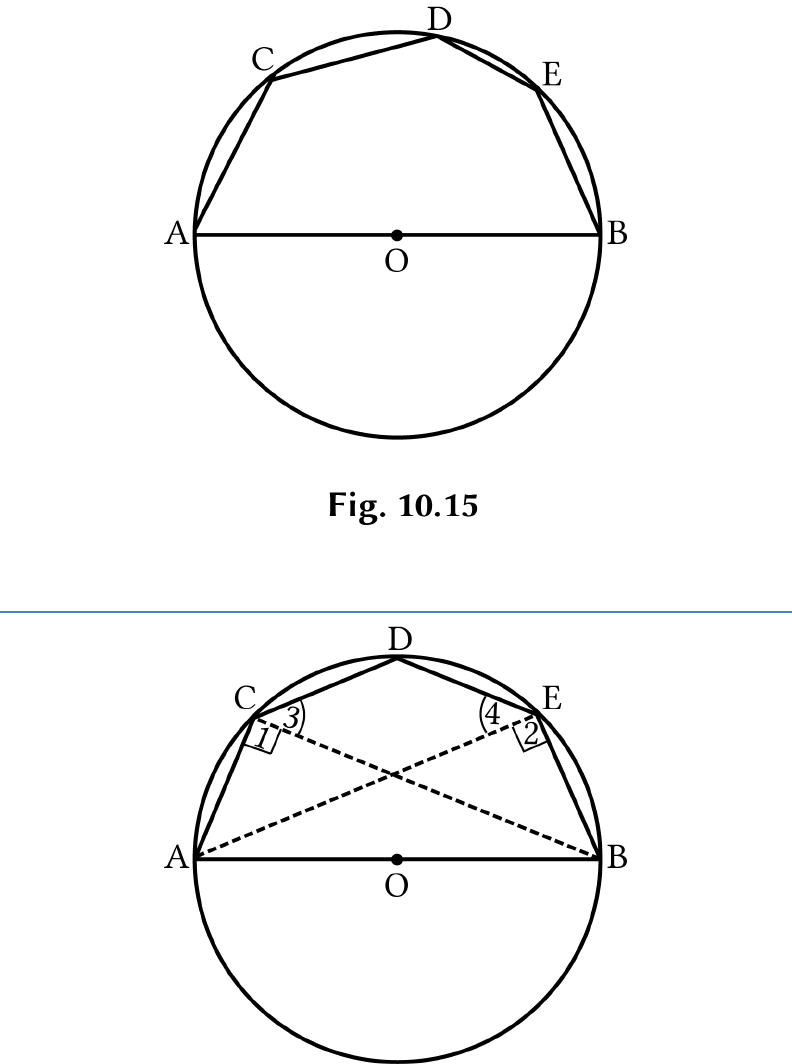
Question: 16
In Fig.10.14,Find
OAB
.
Solution:
It is given that
40 ACB
Now,
2 2 1
(∵ Angle subtended by a segment to
the circle is half the angle subtended to the centre)
2 2 40

2 80
In
OAB
,
OA OB
(Radius of a circle)
4 3
(Isosceles triangle property)
Now,
2 3 4 180
(Angle sum property of∆)
80 3 3 180
2 3 180 80
2 3 100
3 50
50OAB
Question: 17
A quadrilateral
ABCD
is inscribed in a circle such
that
AB
is a diameter and
130ADC
. Find
BAC
.
Solution:

Since
ABCD
is inscribed in a circle,
ABCD
is a cyclic
quadrilateral.
1 2 180
(The sum of opposite angles of a
cyclic quadrilateral is supplementary)
130 2 180
2 180 130
2 50
Now,
3=90
(Angle in the semi-circle is 90
o
)
In
Δ ACB
2 3 4 180
(Angle sum property of a triangle)
50 90 4 180
4 180 140
40 BAC
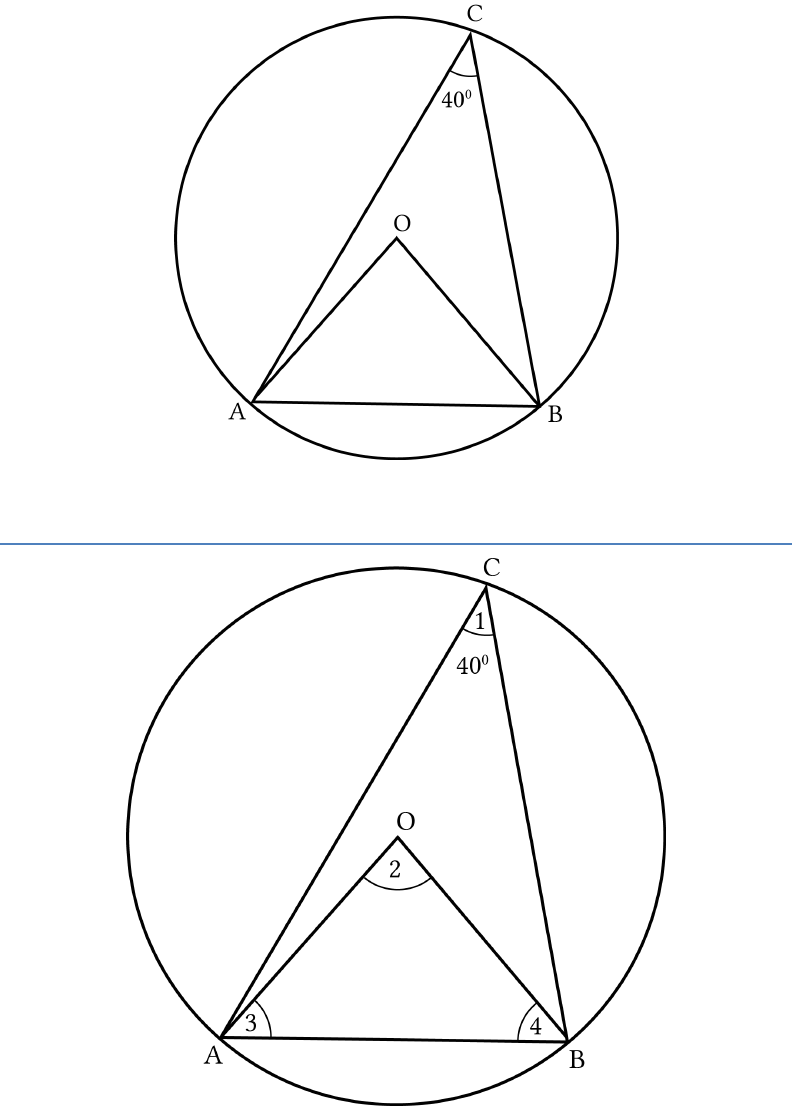
Question: 18
Two circles with centres
O
and
O
intersect at two
points
A
and
B
. A line
PQ
is drawn parallel to
OO
through
A
(or
B
) intersecting the circles at
P
and
Q
.
Prove that
2 .PQ OO
Solution:
First, let us draw
OM PQ
and
'O N PQ
Since
OM
chord
PA
(∵
OM PQ
),
(i)
1
2
PM AM PA....
(Perpendicular drawn from
the centre of a circle to a chord, bisects it)
Similarly,
' chordO N AQ
(ii)
1
2
A N QN QA...

2 2PQ PA AQ AM AN
(Using (i) and (ii))
( )
2( )
2 ..... iii
PQ AM AN
PQ MN
Now,
'PQ OO
(Given)
'OM O N
(Both are the perpendicular distance
between the parallel lines
PQ
and
'OO
)
Therefore
'OMNO
is a parallelogram.
Hence,
(iv)' .....OO MN
(Opposite sides of a
parallelogram)
Using (iii) and (iv), we get
2 'PQ OO
Question: 19
In Fig.10.15,
AOB
is the diameter of a circle and
C
,
D
,
E
are any three points on the semi-circle. Find the
value of
.ACD BED
Solution:
Let us join
AE
and
BC
.
Now,
Angle 2 = 90
o
... (i) (Angle subtended by a diameter
of a circle)
Since
AEDC
is inscribed in a circle,
AEDC
is a cyclic
quadrilateral.
4 180 ACD
.... (ii) (
The sum of opposite angles
of a cyclic quadrilateral)
Adding (i) and (ii)
4 2 180 90
180 90
ACD
ACD BED
270
Question: 20
In Fig. 10.16,
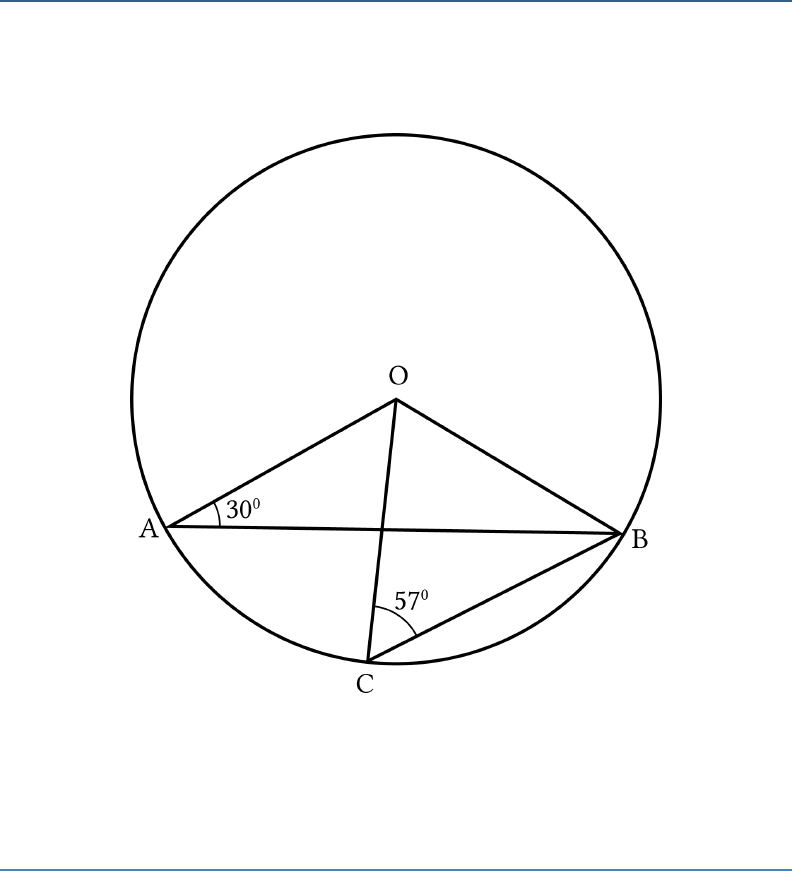
30OAB
and
57OCB
. Find
BOC
and
.AOC
Fig. 10.16
Solution:
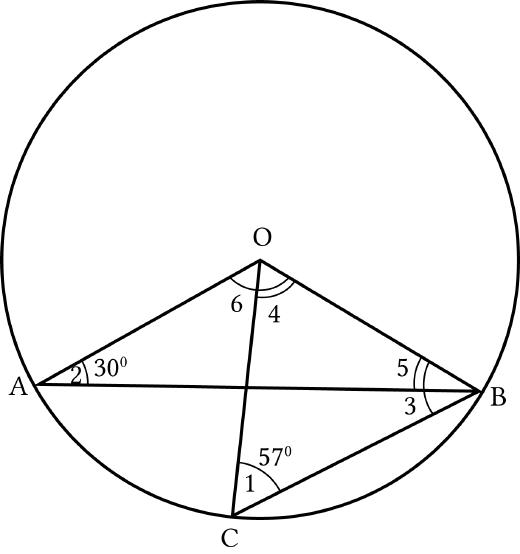
In ∆
OCB,
OB OC
(Both are the radius of a circle)
1 3 57
(Isosceles ∆ Property)
Also,
1 3 4 180
(Angle sum property of a ∆)

57 57 4 180
4 180 114
( )66 .... iBOC
In
OAB
OA OB
(Both are the radius of a circle)
5 2 30
(Isosceles ∆ Property)
Also,
2 5 6 180
(Angle sum property of ∆)
30 30 6 180
6 180 60
( )6 120 .... ii
Now,
6 4
120 66 54
AOC AOB BOC
AOC
Exercise 10.4
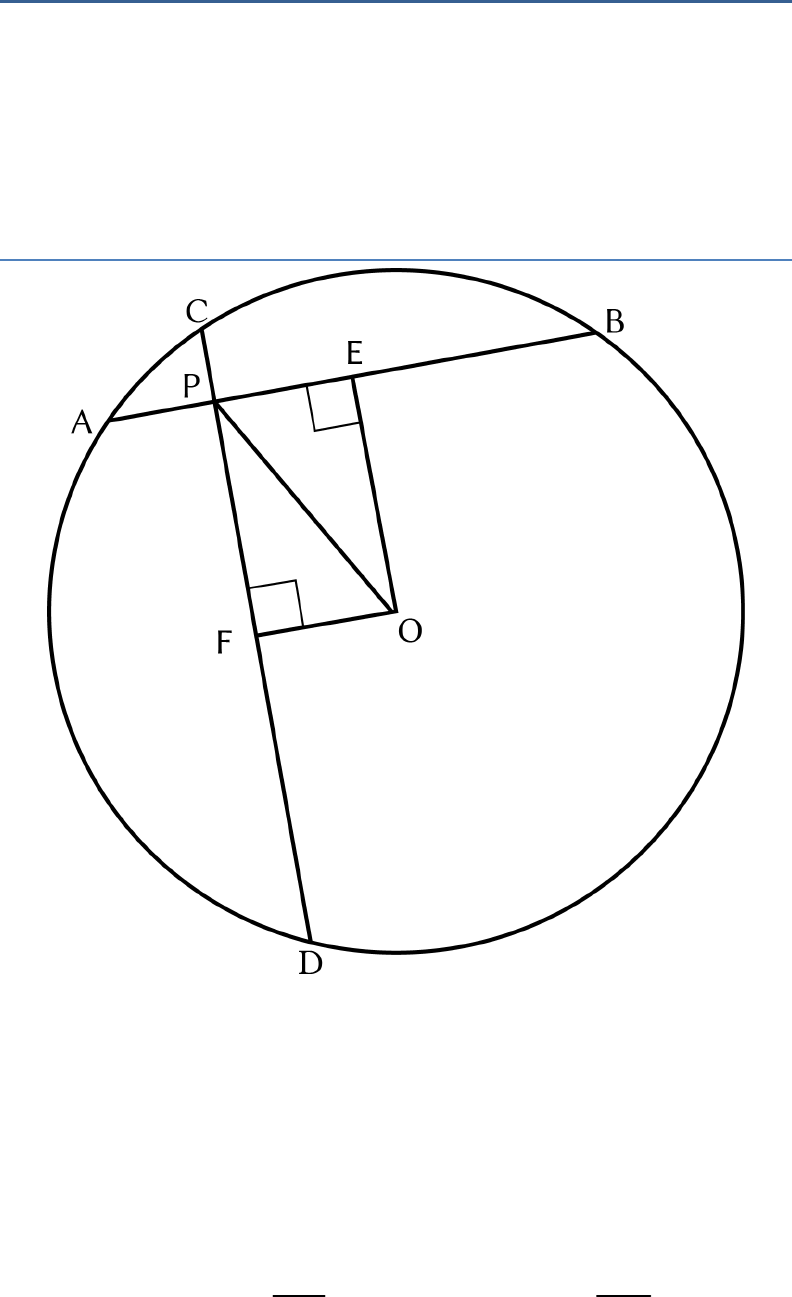
Question: 1
If two equal chords of a circle intersect, prove that
the parts of one chord are separately equal to the
parts of the other chord.
Solution:
Let us consider
AB
and
CD
are two equal chords of a
circle, meet at point
P
.
We need to show that
AP CP
and
BP DP
.
Let us draw
OE AB
and
OF CD
.
Then,
2
AB
AE EB
and
2
CD
CF FD
(Perpendicular drawn from the centre of a circle to a
chord bisects the chord)

Now,
AB CD
(Given)
∴
..(i)
2 2
..
AB CD
EB FD
(Using above result)
In
OPE
and
OPF
,
OEP OFP
(Both are right angles)
OE OF
(Equal chords are equidistant from the
centre)
OP OP
(Common)
OPE POF
by RHS property
Hence,
PE PF
.... (ii)
(By CPCT)
Adding (i) and (ii), we get
(iii)
EB+PE DF+PF
PB=PD....
Now,
AP AB PB CD PD
(
AB CD
(Given)
and using (iii))
( )AP CP CD PD CP
Hence, it is proved.
Question: 2
If non-parallel sides of a trapezium are equal, prove
that it is cyclic.
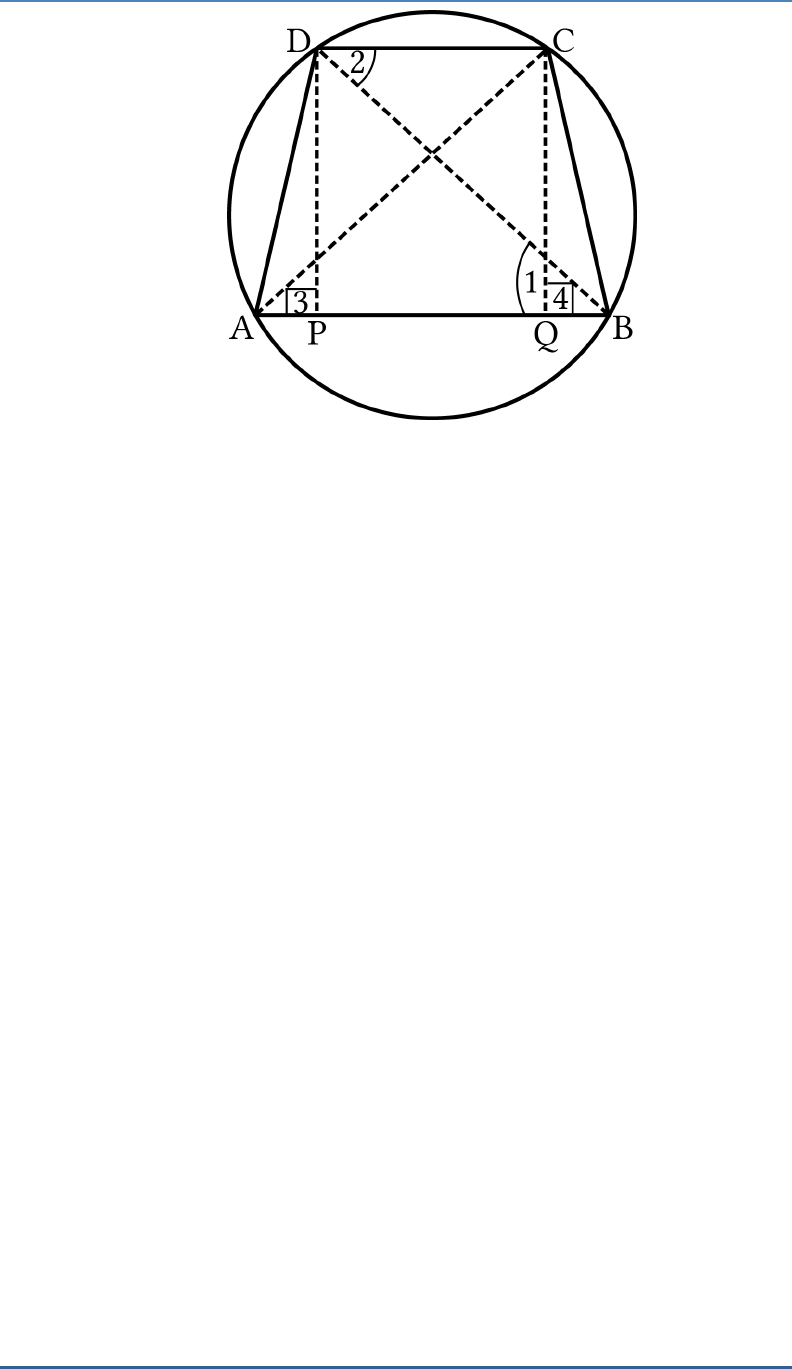
Solution:
Let ABCD be a trapezium in which
AB DC
and
.AD BC
Let us draw
DP AB
and
CQ AB
Now, in
DPA
and
CQB
3 1 90
DA CB
(Given)
DP CQ
(Distance between parallel lines)
DPA CQB
(By R.H.S property))
Thus,
A B
(By CPCT)
But,
180B C
(
AB CD
and BC is a transversal)
180A C
ABCD
is cyclic
Question: 3
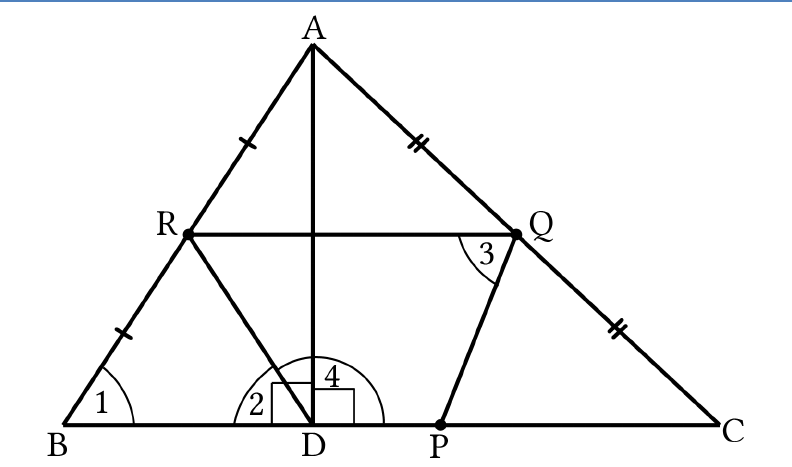
If
P
,
Q
and
R
are the mid-points of the sides
BC
,
CA
and
AB
of a triangle and
AD
is the perpendicular
from
A
on
BC
, prove that
P
,
Q, R
and
D
are concyclic.
Solution:
Let us join
RQ, QP
and
RD
.
R
is the midpoint of hypotenuse
AB
of right angle
ADB
(
AD BC
)
RB RD
(
Midpoint of the hypotenuse is
equidistant from all 3 vertices in a right angles
triangle)
Therefore, in
DBR
........ i2 1
(Isosceles triangle property)
Now,
RQ
joins midpoint of sides
AB
and
AC
respectively in
ABC
.
RQ BC
(Midpoint theorem)
RQ BP

Similarly,
QP RB
is BPQR gm
So,
...(ii)1 3
(Opposite angles of a
gm
)
From (i) and (ii), we have
2 3
But
2 4 180
(linear pair axiom)
3 4 180
PQRD
is cyclic
Thus, the points
P
,
Q
,
R
,
D
are concyclic.
Question: 4
ABCD
is a parallelogram. A circle through
A
,
B
is so
drawn that it intersects
AD
at
P
and
BC
at
Q
. Prove
that
P, Q
,
C
and
D
are concyclic.
Solution:
Let us join
PQ
.
1 A
(Exterior angle property of cyclic
quadrilateral)

But
A C
(Opposite angles of a
gm
)
1 C
But,
180 C D
(Adjacent angles of a parallelogram)
1 180D
QCDP
is cyclic
Thus, points
P, Q, C, D
are concylic.
Question: 5
Prove that if the angle bisector of any angle of a
triangle and perpendicular bisector of the opposite
side intersect, they will intersect on the circumcircle
of the triangle.
Solution:
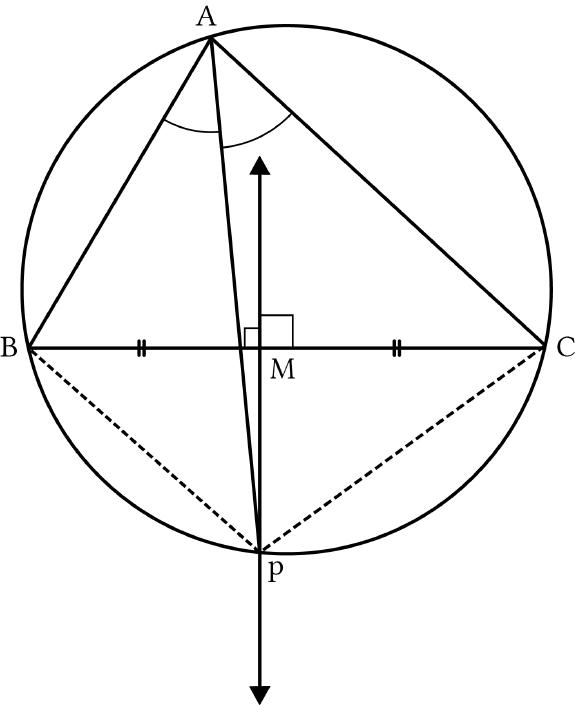
Let ABC be a triangle inscribed in a circle.
Let angle bisector of
A
and perpendicular bisector
of
BC
intersect at point
P
.
We need to prove that
A, B, P
and
C
are concyclic.
Let us join
BP
and
CP
.
We know that any 3 points are concyclic.
Therefore,
A, B, C
are concyclic.
Let us assume that P lies outside the circle.
Now, in
BMP
and
CMP
,
MP=MP
(Common)
BMP CMP
(Each right angle)
BM=CM (MP
is perpendicular bisector of
BC
)
Thus,
BMP CMP
(By SAS Rule)

So,
BP=CP
(By CPCT)…..(i)
Also,
BAP CAP
(Given).... (ii)
From (i) and (ii), we can say that P lies on the circle
as equal chords of a circle subtend equal angle at the
at the centre and also, the angle subtended by a
chord at the centre is twice the angle subtended by it
at the remaining part of the circle. Thus, equal
chords subtend equal angle at the circle.)
Hence,
A, B, C
and
P
are concyclic.
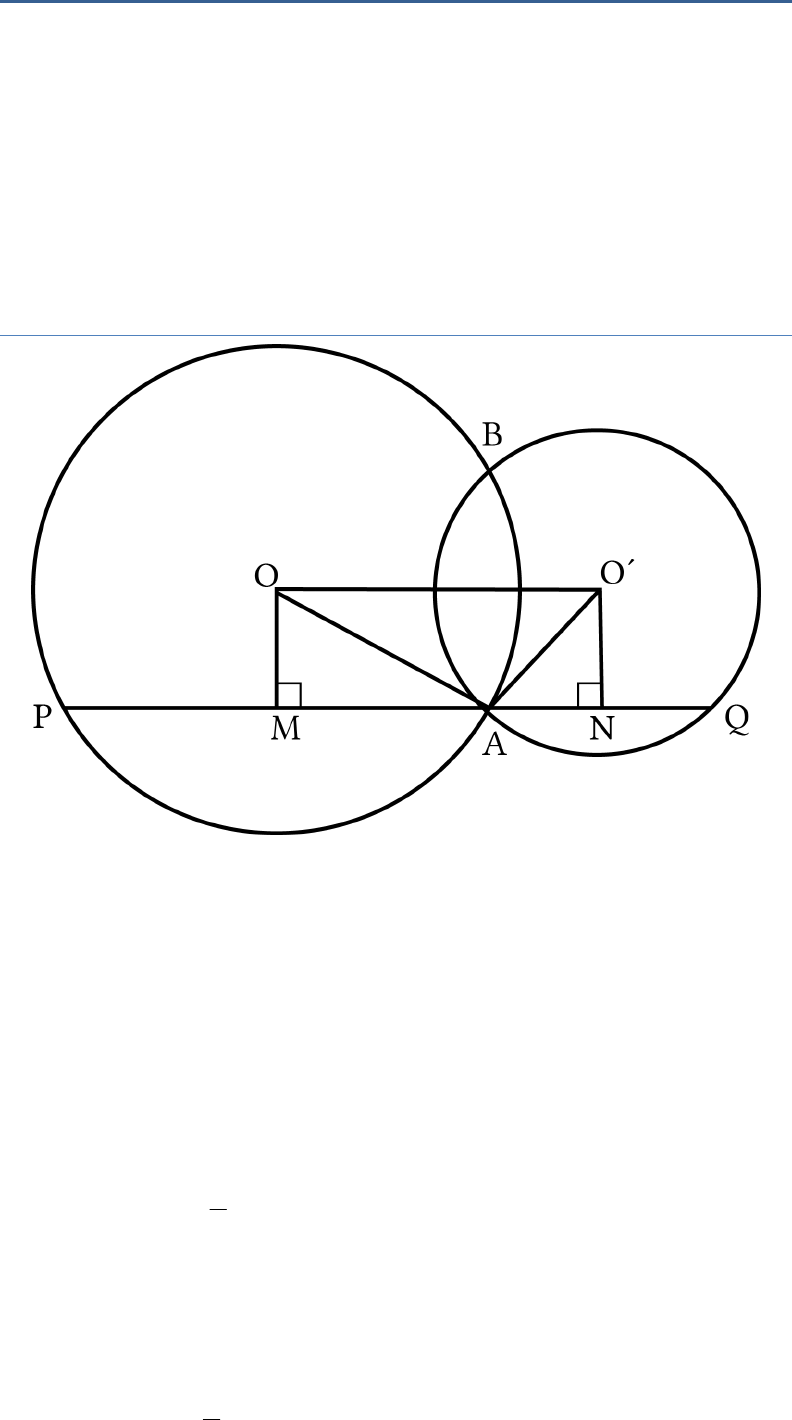
Question: 6
If two chords
AB
and
CD
of a circle
AYDZBWCX
intersect at right angles (See Fig.10.18), prove that
arc
CXA
arc
DZB
arc
AYD
arc
BWC
semicircle.

Fig.10.18
Solution:
Let the chords
AB
and
CD
of a circle
AYDZBWCX
intersect at
T
.
Let us draw a diameter
MN CD
.
Let the centre be
O
.
Since
MN CD
, arc
CM
=arc
DN.
....(i)
Also, arc
MCXA
= arc
MWB
(Symmetrical about
diameter of a circle)
And arc
AN
= are
NB
.... (ii)
Now,
MN i
s a diameter.
So, arc
MCXAYDN
= arc
MWBZN
= semicircle..... (iii)
Now,
arc arc arc MCXAYDN MC CXA arc AN
arc arc arc DN CXA NB
arc arc CXA DNB
arc arc ....CXA DZB iv
arc = arc arc MWBZN MWB NB
arc arc MWB AN
(Using (i) and (ii))
arc arc arc arc ( ) ( )CWB CM AYD DN
arc arc arc arc CWB CM AYD CM
arc arc ....CWB AYD v
Using (iii), (iv) and (v), we get
arc
CXA
arc
DZB
arc
AYD
arc
BWC
semicircle
Hence, it is proved.

Question: 7
If
ABC
is an equilateral triangle inscribed in a circle
and
P
be any point on the minor arc
BC
which does
not coincide with
B
or
C
, prove that
PA
is an angle
bisector of
BPC
.
Solution:
Since ABC is an equilateral triangle.
So,
( ).... i ABC ACB
Now,
ABC
and
APC
are the angles in the same
segment
AC
( ).... ii ABC APC
Similarly,
( ).... iii ACB APB

Using (i), (ii) and (iii), we get
APC APB
Thus,
PA
is an angle bisector of
BPC
.
Question: 8
In Fig. 10.19,
AB
and
CD
are two chords of a circle
intersecting each other at point
E
.
Prove that
1
2
AEC
(Angle subtended by arc
CXA
at centre + angle subtended by arc
DYB
at the
centre).
Solution:

We need to show that
1
( )
2
AEC AOC DOB
Let us join
AC, BC
and
BD
.
In
CEB
,
AEC ECB CBE
(Exterior angle property)
AEC DCB ABC
.....(i)
Since AC is a chord,
2 AOC ABC
..... (ii) (Angle subtended by the
chord AC )
Similarly,
2 DOB DCB
....(iii) (Angles subtended
by the chord BD)
Adding (ii) and (iii)
2( ) AOC DOB ABC DCB
.... (iv)
Now, using (i) in (iv),
)
2
1
(
2
AOC DOB AEC
AOC DOB AEC
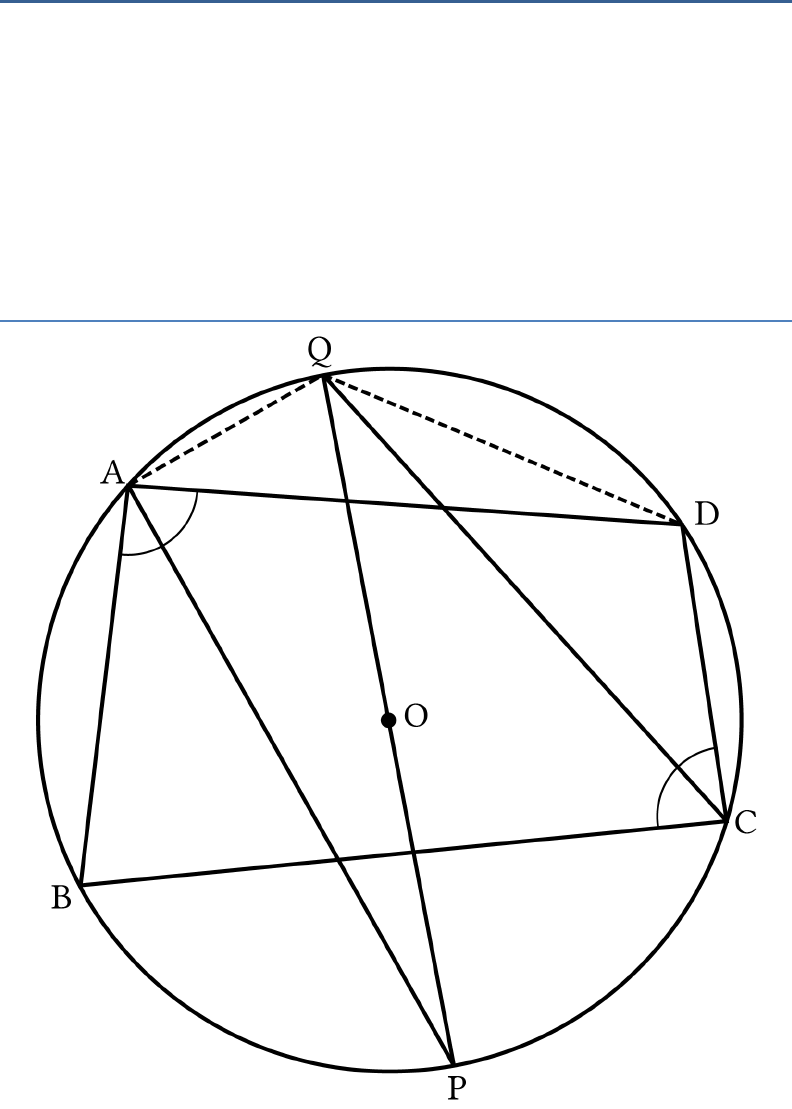
Question: 9
If bisectors of opposite angles of a cyclic
quadrilateral
ABCD
intersect the circle,
Circumscribing it at the points
P
and
Q
, prove that
PQ
is a diameter of the circle.
Solution:

To prove that
PQ
is the diameter of the circle, we
need to prove that
90 PAQ
.
Let us join
AQ
and
QD
.
Since
ABCD
is a cyclic quadrilateral,
180A C
(Opposite angles of a cyclic
quadrilateral are supplementary)
90
2 2
A C
...(i)
It is given that
AP
bisects
A
and
CQ
bisects
C
.
So,
90PAD DCQ
....(i)
Also,
DCQ DAQ
...(ii) (Angles in the same segment
DF)
On comparing (i) and (ii), we have
90
90
PAD DAQ
PAQ
PAQ
is the angle in a semi-circle.
PQ
is the diameter of the circle.

Question: 10
A circle has radius
2
cm. It is divided into two
segments by a chord of length 2cm.
Prove that the angle subtended by the chord at a
point in major segment is 45°.
Solution:

Let us consider a circle with centre O and
radius
2
cm.
Let
2BC
cm be the chord and let
A
be the point in major segment.
We need to show that
45BAC
In
OBC
2 2
2 2
2 2 OB OC
2
2 2 4 (2)
2 2 2
OB OC BC
Thus, by reverse of Pythagoras theorem,
OBC
is a right angle triangle,
So,
90BOC
Now,
1
2
BAC BOC
(Angle subtended by a chord on
the centre is double of the angle subtended by same
chord on circumference)
90
45
2
BAC
Question: 11
Two equal chords
AB
and
CD
of a circle when
produced intersect at a point
P
.
Prove that
.PB PD
Solution:

Let us draw
OM AB
and
ON CD
Since
OM AB
,
2
AB
AM MB
…. (i) (Perpendicular from the
centre to a chord bisects it.)
Similarly,
2
CD
CN ND
… (ii)
Now,
AB CD
(Given)
2 2
AB CD
...(iii) MB ND
(Using (
i
) and (
ii
))
In
OMP
and
,ONP
1 2 90
OP OP
(Common)
OM ON
(Equal chords are equidistant from the centre)
OMP ONP
(By RHS property)
...(iv) MP NP
(By CPCT)
Subtracting (iii) from (iv), we get
MP MB NP ND

PB PD
Question: 12
AB
and
AC
are two chords of a circle of radius
r
such
that
2AB AC
. If
p
and q are the distances of
AB
and
AC from the centre, prove that
2 2 2
4 3 .q p r
Solution:
Let
2AC a
then
4AB a
.
Since
,ON AC
2
2
a
AN a
(Perpendicular from the centre to a
chord bisects it)
Similarly,
,OM AB

4
2
22
a
a
AB
AM
In
ANO
,
90ANO
2 2 2
r q a
(By Pythagoras theorem)
...(i)
2 2 2
a r q
In
AMO
,
90AMO
(ii)
2 2 2
(2 ) .....r p a
(By Pythagoras theorem)
2 2 2
4 r p a
2 2 2 2
4( ) r p r q
(Using (i))
2 2 2 2
4 4 r p r q
2 2 2 2
4 4 q r p r
2 2 2
4 3q r p
Hence proved.
Question: 13
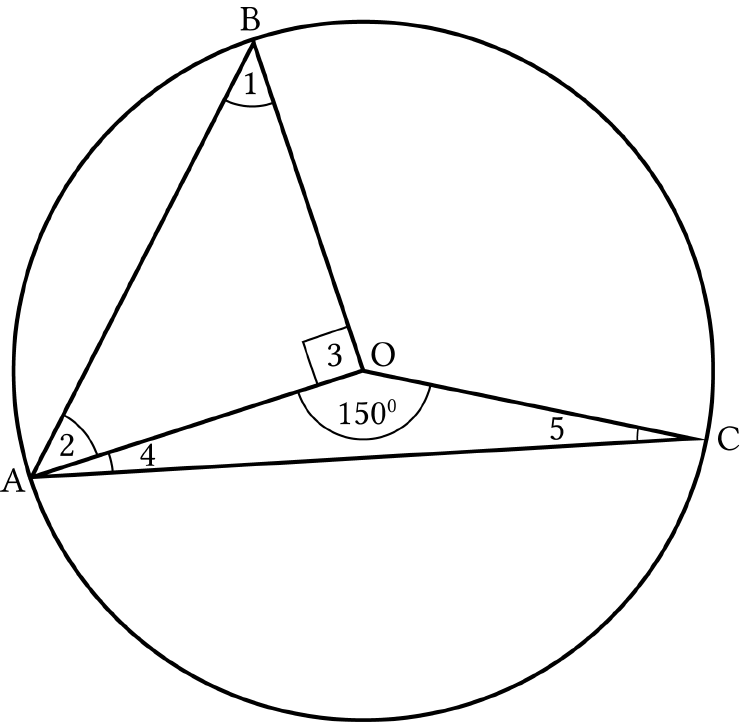
In Fig. 10.20, O is the centre of the circle,
30 .BCO
Find
x
and
y
.
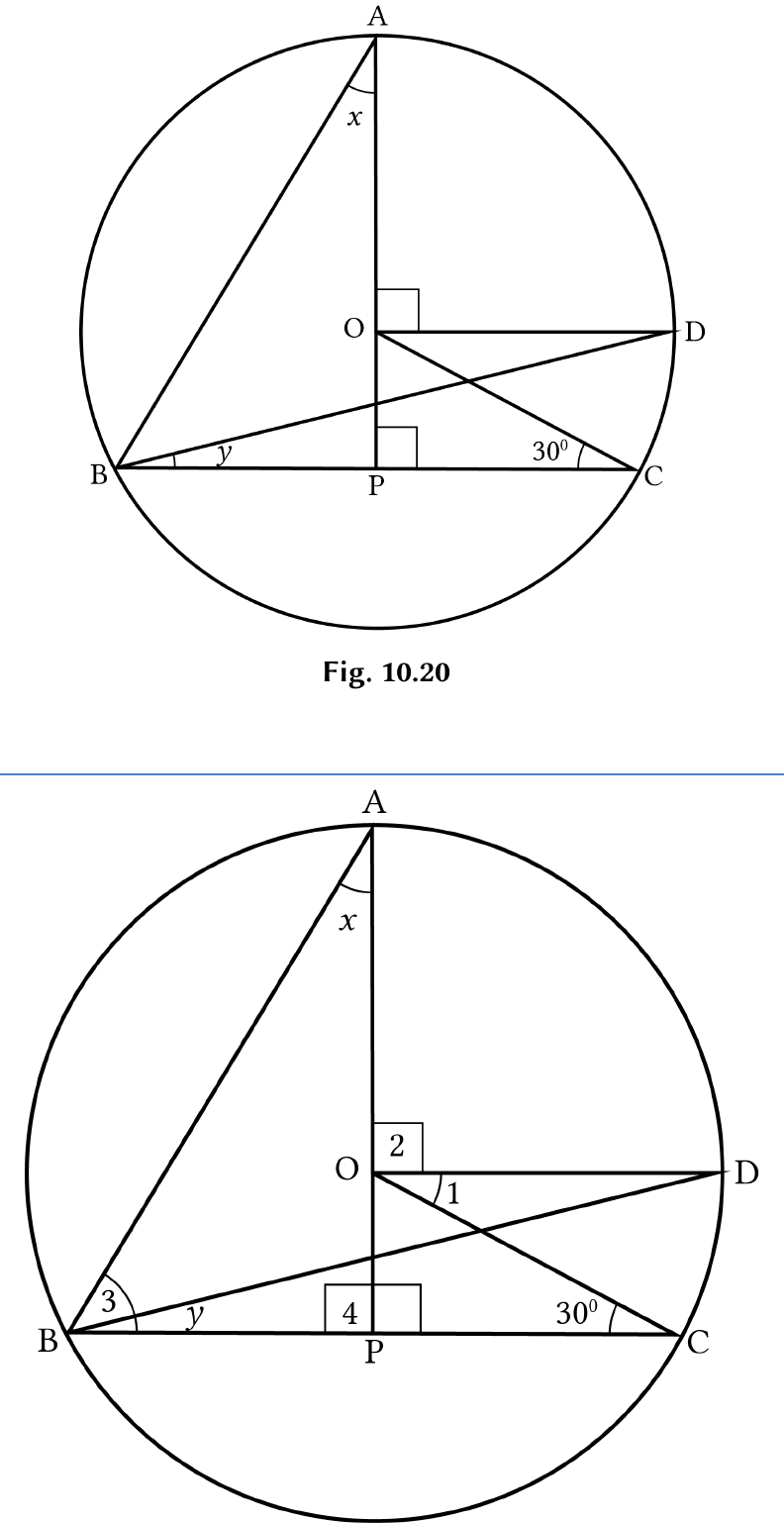
Solution:
In
OPC
,
180OPC PCO POC
(Angle sum property)
90 30 180
180 120 60
POC
POC
Now,
1 POD POC
90 60
30
…(i)
CD
subtends
1
at the centre and
y
on
circumference.
1 2y
30 2 y
(Using (i))
15 y
arc
AD
subtends
2
at the centre and
3
on
circumference.
2 2 3
But
2 90
3 45
…(ii)
In the right angle
APB
,
4 180 x ABP
(Angle sum property of ∆)
( 3 ) 90 180 x y
45 15 90 180 x
(Using (ii))
180 150 x
30 x
Question: 14
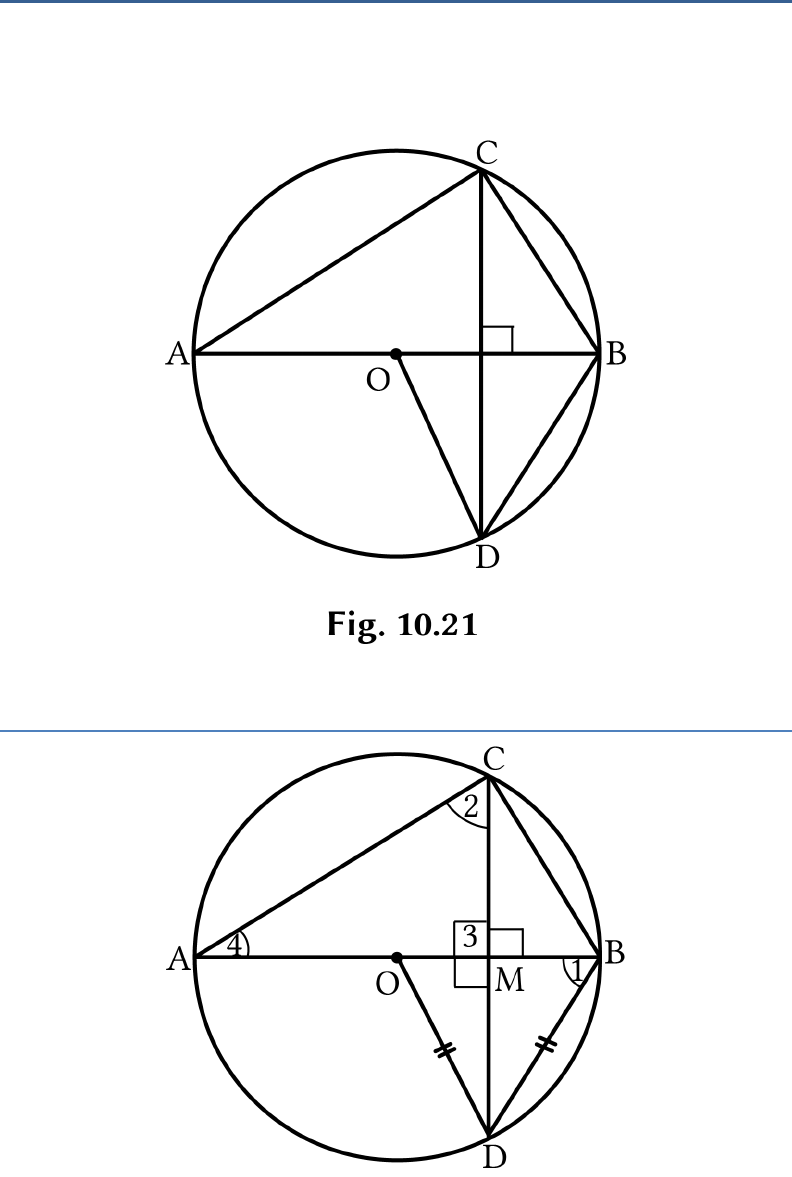
In Fig. 10.21, O is the centre of the circle,
BD OD
and
CD AB
. Find
.CAB
Solution:
It is given that
BD OD
But
OD OB
(Both are radius)
So, in
OBD
BD OD OB
is an equilateral triangle. OBD
1 60
(Angle of an equilateral triangle)
But
2 1
(Angle in same segment)
2 1 60
In
CAM
,
2 3 4 180
(Angle sum property of a
triangle)
60 90 4 180
1504 180
30 CAB