
Lesson: Constructions
Exercise 11.1 (5)
Question: 1
Construct an angle of 90° at the initial point of a
given ray and justify the construction.
Solution:
Steps of construction:
1. Let us draw a ray
OX
.
2. With
O
as a centre and any radius, let us draw an
arc ABC cutting
OX
at
A
.
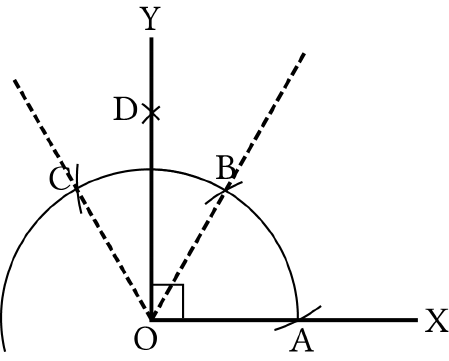
3. With B as a centre and the same radius, let us
mark a point B on the arc
ABC
. (By construction
= 60AOB
)
4. With B as a centre and the same radius, let us
mark a point
C
on the arc
ABC
. (By construction
= 60BOC
)
5. With B and C as centres, let us draw two arcs
intersecting each other with the same radius at
D.(By construction
=BOD COD
)
6. Let us join
O
and
D
to form a ray
OD
.
7.
AOD
= 90°
Justification for construction:

= 120° = 60 , = 60 :
=
= =
1
= 60
2
= 30
Now, =
= 60
(
30 =
)
(
90
)
AOC AOB BOC
BOC BOD DOC
BOD BOC BOD DOC
BOD
BOD
AOD AOB BOD
Question: 2
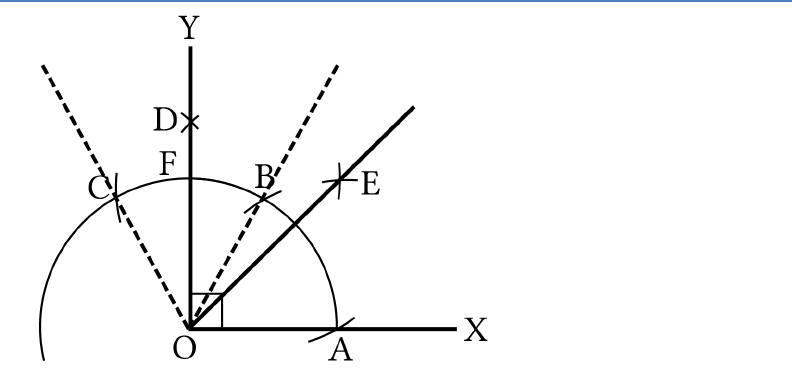
Construct an angle of 45° at the initial point of a
given ray and justify the construction.
Solution:
Steps of construction:
1. Let us draw a ray
OX
.
2. With
O
as a centre and any radius, let us draw an
arc ABC cutting
OX
at
A
.
3. With B as a centre and the same radius, let us
mark a point B on the arc
ABC
. (By construction
60AOB
)
4. With
B
as a centre and the same radius, let us
mark a point C on the arc
ABC
. (By construction
60BOC
)
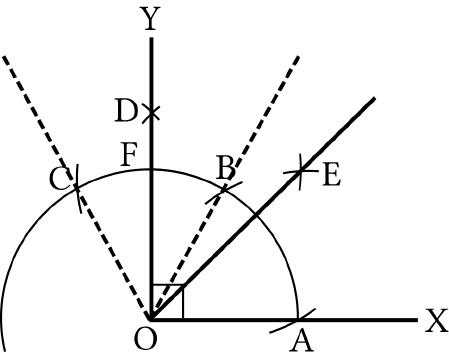
5. With
B
and
C
as centres, let us draw two arcs
intersecting each other with the same radius at
D.(By construction
BOD COD
)
6. Let us join
O
and
D
to form a ray
OD
.
7.
AOD
= 90°
8. With
A
and
D
as centres, let us draw two arcs
intersecting each other with the same radius at
E
.
9.
AOE
= 45°
Justification for construction:

= 120 = 60 , = 60 :
=
1
= =
2
1
BOD = ×60
2
BOD = 30
Now,
= +
= 60 + 30 = 90
1
=
2
= as
( )
is the angle b
(
( se t
)
i c
AOC AOB BOC
BOC BOD DOC
BOD BOC BOD DOC
AOD AOB BOD
AOE AOD
AOE DOE OE
or
1
= of 90
2
)
= 45
Question: 3
Construct the angles of the following measurements:
(i) 30°

(ii) 22.5°
(iii) 15°
Solution
(i) 30°
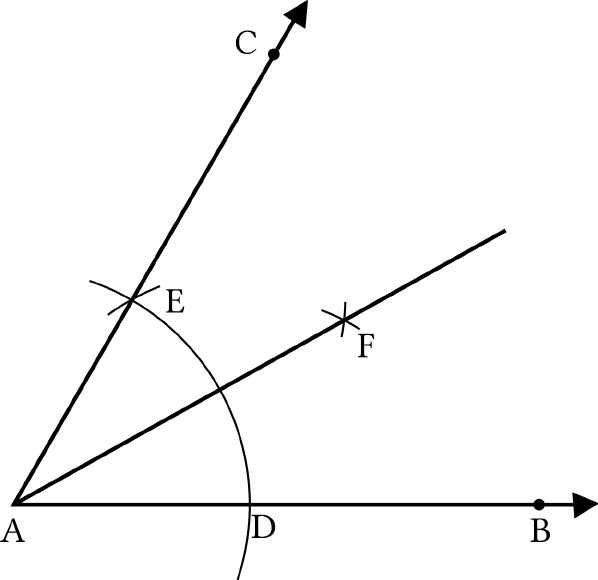
Steps of construction:
1. Let us draw a ray
AB
.
2. With A as a centre and any radius, let us draw an
arc cutting
AB
at
D
.
3. With
D
as a centre and the same radius, let us
mark a point
E
on the arc.(By construction
= 60BAE
)
4. With D and E as centres, let us draw two arcs
intersecting each other with the same radius at
F(By construction
DAF EAF
)

5. Let us join
A
and
F
to form a ray
AF
that makes
an angle 30° with
AB
(ii) 22.5°
120 60 , 60 :
1
60
2
3
( )
0
( )
AOC AOB BOC
BOC BOD DOC
BOD BOC BOD DOC
BOD
BOD

Now
as is the angle bisector
as is the angle bisector
60 30 90
1
2
1
90 45
2
1
2
( )
1
45 22
(
.5
2
)
AOD AOB BOD
AOE AOD
AOE DOE OE
of
AOG AOE
AOG GOE OG
of
(iii) 15°

Steps of construction:
1. Let us draw a ray AB.
2. With A as a centre and any radius, let us draw an
arc cutting
AB
at
D
.
3. With
D
as a centre and the same radius, let us
mark a point
E
on the arc.(By construction
60BAE
)
4. With
D
and
E
as centres, let us draw two arcs
intersecting each other with the same radius at
F
(By construction
DAF EAF
)
5. Let us join
A
and
F
to form a ray
AF
making an
angle 30° with
AB
.
6. With D and G as centres, let us draw two arcs
intersecting each other with the same radius at

H
(By construction
DAH FAH
) Let us join A
and
G
to form a ray
AG
that makes an angle15°
with
AB
Question: 4
Construct the following angles and verify by
measuring them by a protractor:
(i) 75°
(ii) 105°
(iii) 135°
Solution
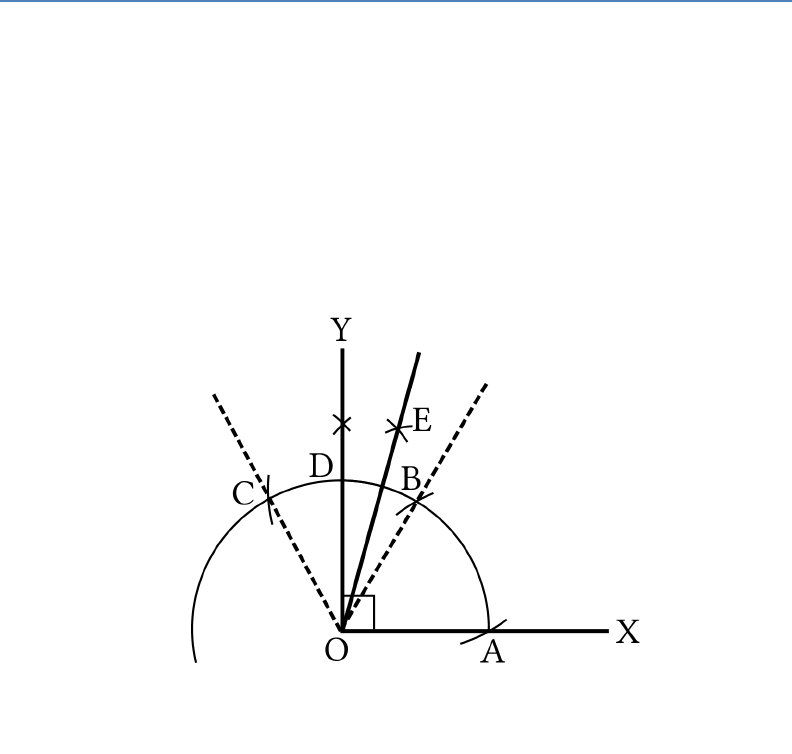
(i) 75°
Steps of constructions:
1. Let us draw a ray
OX
.
2. With
O
as a centre and any radius, let us draw an
arc ABC cutting
OX
at
A
.
3. With
B
as a centre and the same radius, let us
mark a point
B
on the arc
ABC
.(By construction
∠AOB = 60°)
4. With B as a centre and the same radius, let us
mark a point C on the arc ABC. (By construction
60BOC
5. With
B
and
C
as centres, let us draw two arcs
intersecting each other with the same radius at
D
.(By construction
BOD COD
6. Let us join
O
and
D
to form a ray
OD
.
7.
AOD
90°
8. With
B
and
D
as centres, let us draw two arcs
intersecting each other with the same radius at
E
.
9.
AOE
=75°

.
(ii) 105°
Steps of constructions:
1. Let us draw a ray
OX
.
2. With O as a centre and any radius, let us draw an
arc ABC cutting
OX
at
A
.
3. With
B
as a centre and the same radius, let us
mark a point B on the arc
ABC
. (By construction
60AOB
)
4. With B as a centre and the same radius, let us
mark a point C on the arc
ABC
. (By construction
60BOC
)
5. With
B
and
C
as centres, let us draw two arcs
intersecting each other with the same radius at
D
.(By construction
BOD COD
)
6. Let us join
O
and
D
to form a ray
OD
.

7.
AOD=
90°
8. With
B
and
C
as centres, let us draw two arcs
intersecting each other with the same radius at
E
.
9.
AOE
=105°
(iii) 135°
Steps of constructions:
1. Let us draw a ray
OX
.
2. With
O
as a centre and any radius, let us draw
an arc ABC cutting
OX
at
A
and
E
.
3. With
B
as a centre and the same radius, let us
mark a point
B
on the arc
ABC
. (By construction
60AOB
)
4. With
B
as a centre and the same radius, let us
mark a point C on the arc
ABC
. (By
construction
60BOC
)
5. With
B
and
C
as centres, let us draw two arcs
intersecting each other with the same radius at
D
.(By construction
BOD COD
)
6. Let us join
O
and
D
to form a ray
OD
.
7.
AOD
= 90°
8. With
D
and
E
as centres, let us draw two arcs
intersecting each other with the same radius at
F
.
9.
AOF
=135°

Question: 5
Construct an equilateral triangle, given its side and
justify the construction.
Solution
Let us consider a ray
AB
with initial point
A
, as
shown below.
We want to construct a ray AC such that
60 .CAB
Steps of Construction:
1. Taking
A
as centre and any radius draw an arc
that intersects
AB
, say at point
D
.
2. Taking
D
as centre and with the same radius as
before, draw an arc intersecting the previously
drawn arc, say at point
E
.
3. Draw a ray from
A
passing through
E
. Then
CAB
is the required angle of 60°.
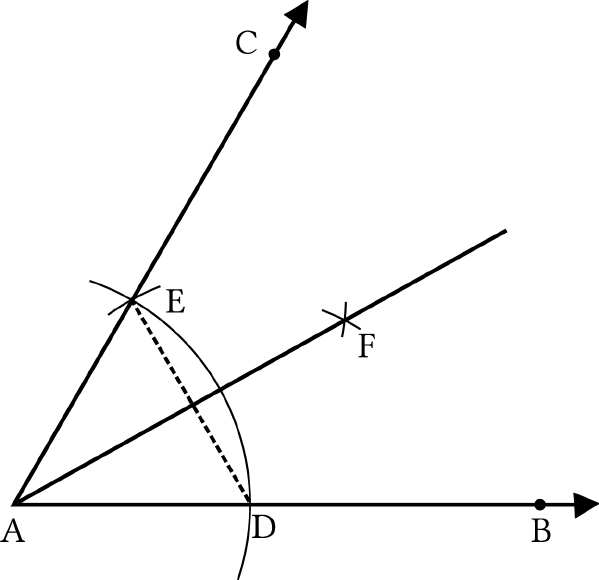
Proof that this method gives the required angle
of 60°:
Join
DE
.
So,
AE
=
AD
=
DE
(Same radius)
This means Δ
EAD
is an equilateral triangle and
therefore
EAD
is equal to 60°. Now
60 .CAB EAD
Hence proved.

Exercise 11.2 (5)
Question: 1
Construct a triangle ABC in which
BC
= 7 cm,
75B
and
AB
+
AC
= 13 cm.
Solution:
Steps of Construction:
1. Let us draw a line segment BC of 7 cm.
2. At point
B
, let’s construct an angle
75 .XBC
3. Let us cut the line segment
BD
13 cm on
.BX AB AC
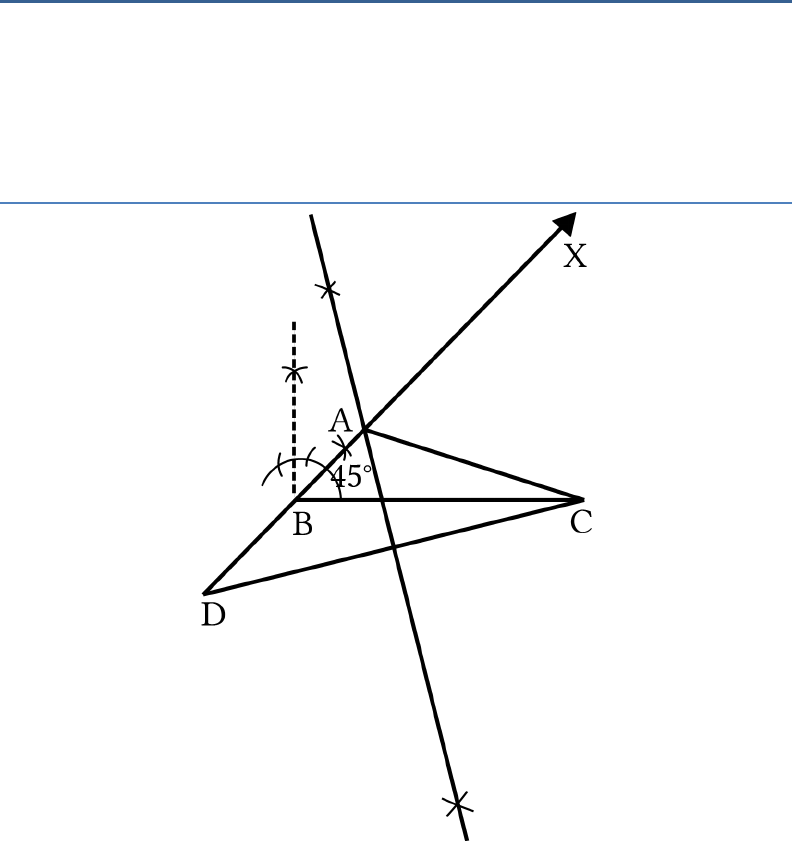
4. Let us join DC and make
.DCY BDC
5. Let
CY
intersect
BX
at
A
.
Thus, Δ
ABC
is the required triangle.
Question: 2
Construct a triangle
ABC
in which
BC
= 8
cm,
45B
and AB
AC = 3.5 cm.
Solution:
Steps of Construction:
1. Let us draw a line segment
BC
= 8 cm .
2. At point B, let’s make an angle of 45° i.e.
XBC
.
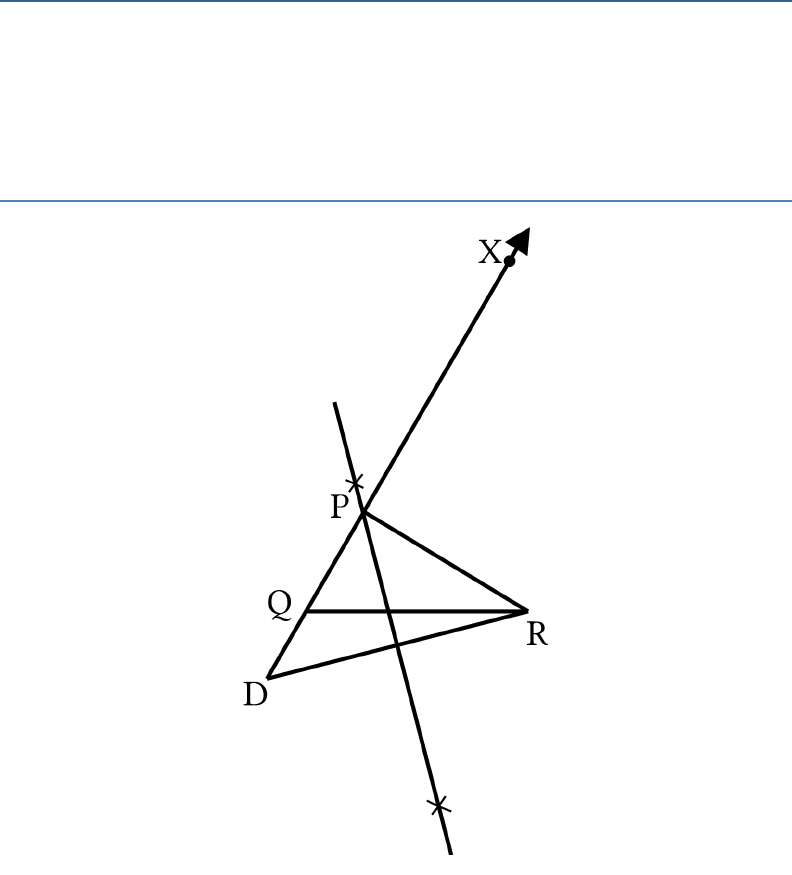
3. Let us cut the line segment
BD
= 3.5 cm (equal to
AB
AC
) on ray
BX
.
4. Let’s join
DC
and draw the perpendicular bisector
of
DC
.
5. Let it intersect
BX
at point
A
.
6. Let us join
AC
.
Thus, Δ
ABC
is the required triangle.
Question: 3
Construct a triangle
PQR
in which
QR
= 6cm,
60Q
and
PR
–
PQ
= 2cm.
Solution:

Steps of Construction:
1. Let’s draw a ray
QX
and cut off a line segment
QR
= 6 cm from it.
2. Let us construct a ray
QX
making an angle of 60º
with QR and produce XQ is produced it to
D
such
that
QD
=
PR – PQ
= 2cm.
3. Let us draw a perpendicular bisector of
DS
intersecting
QX
at a point
P
. and join
PR
is joined.
Thus, Δ
PQR
is the required triangle.
Question: 4
Construct a triangle XYZ in which
30 , 90Y Z
and
XY
+
YZ
+
ZX
= 11 cm.
Solution:
Steps of Construction:
1. Let us draw a line segment
YZ
= 11 cm. (
XY
+
YZ
+
ZX
= 11 cm).
2. We will draw an angle,
30ZYM
at point A
and an angle
90YZN
at point B.
3. We will bisect
XYM
and
YZN
. The bisectors of
these angles intersect each other at point X.
4. We will construct the perpendicular bisectors
PQ
of
XY
and
RS
of
XZ
intersecting the segment
YZ
at
Y
and
Z
respectively.
5. Thus, Δ
XYZ
is the required triangle.
Question: 5
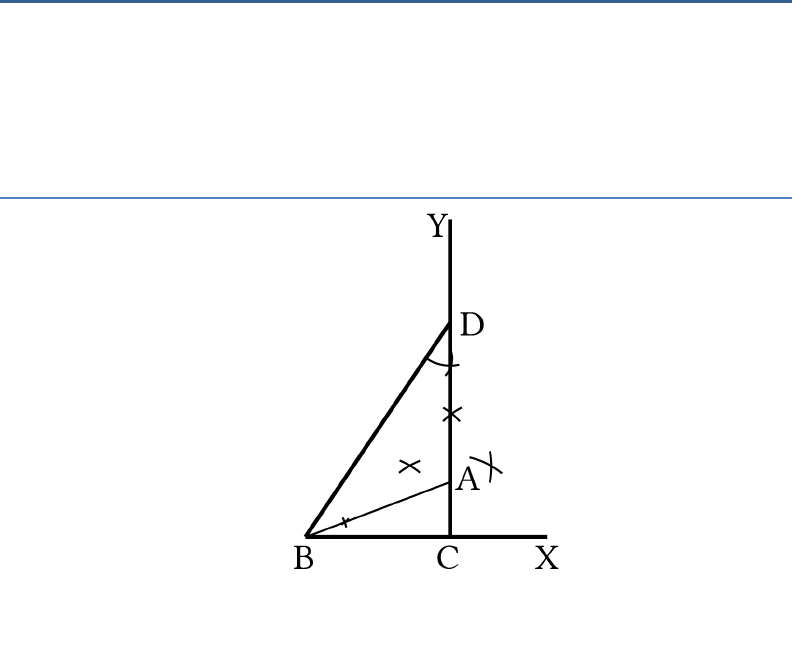
Construct a right triangle whose base is 12 cm and
sum of its hypotenuse and other side is 18 cm.
Solution:
Steps of Construction:

1. We draw a ray BX and a cut off a line segment BC
= 12 cm on it.
2. We construct
90 .BCY
3. We cut off a line segment
CD
= 18 cm on
CY
.
4. We join.
BD
5. We make
ABD
equal to
BDC
Thus, Δ
ABC
is the required triangle.