
Lesson: Heron's Formula
Exercise 12.1
Question: 1
A traffic signal board, indicating 'SCHOOL AHEAD',
is an equilateral triangle with side 'a'. Find the area of
the signal board, using Heron’s formula. If its
perimeter is 180 cm, what will be the area of the signal
board?
Solution
Let the length of the side of the equilateral triangle be
a.
∴ The perimeter of the equilateral triangle
3a 180 cm
cm60a

Semi perimeter of the signal board
a3
2
3
2
a
s
Using Heron's formula,
the area of the signal board =
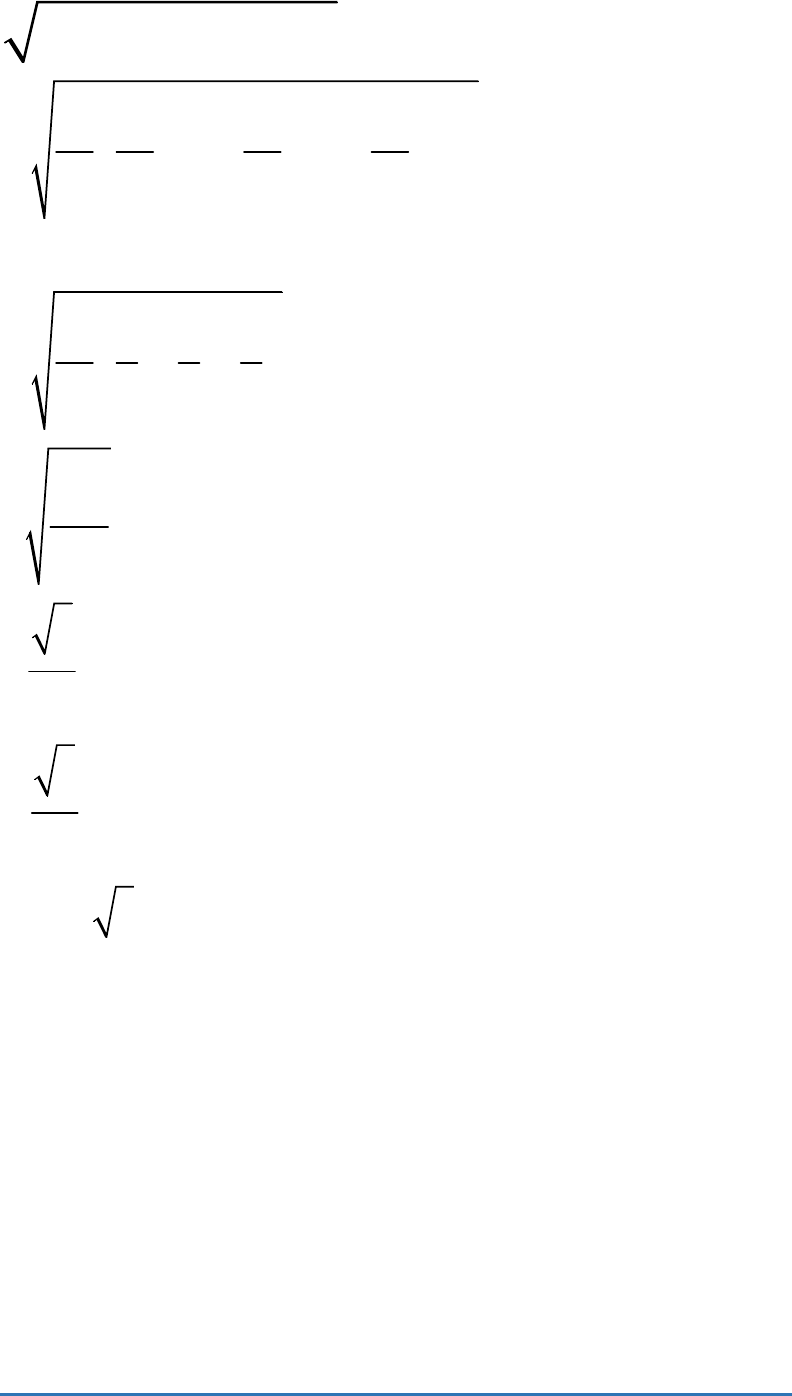
2
2
4
( )
=
=
4
4
Sides of an equilateral triangle are equal
cm
3 3 3 3
2 2 2 2
3
2 2 2 2
-
60
3
1
60
900 3
6
3
3
a a a a
a a a
a a
s s a s
a a
a
b s c
a
Question: 2
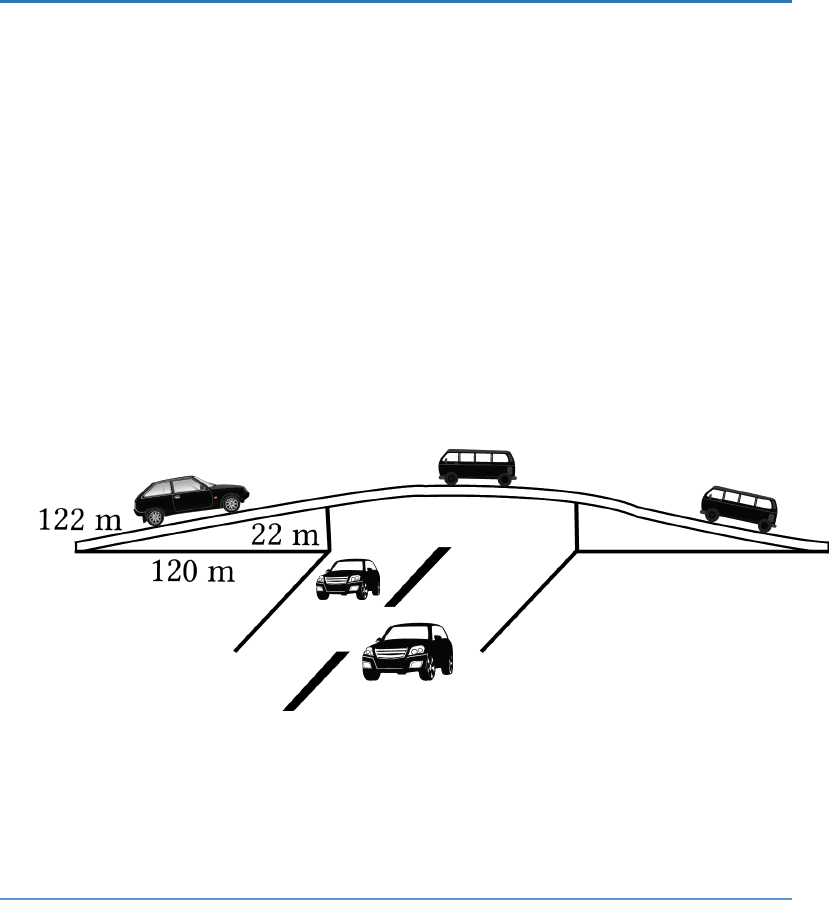
The triangular side walls of a flyover have been used
for advertisements. The sides of the walls are 122 m,
22 m and 120 m (see Fig. 12.9). The advertisements
yield an earning of Rs 5000 per m
2
per year. A
company hired one of its walls for 3 months. How
much rent did it pay?
Fig.
12.9
Solution
The sides of the triangle are 122 m, 22 m and 120 m.
Hence,
, , and122 m 22 m 120 m.a b c
The perimeter of the triangle is
m.122 22 120 264
The semi perimeter of the triangle (s)
m264 / 2 132
s 132
By Heron's formula,

Area of the triangular wall =
2
s s a s b s c
2
132(132 122)(132 22)(132 120)
132 10 110 12 m
1320 m
Earning due to advertising per year =
5000Rs
per m
2
Hence, the rent of one wall for 3 months
Rs Rs1320 5000 3( / 12 165000) 0
Question: 3
There is a slide in a park. One of its side walls has
been painted in some colour with a message “KEEP
THE PARK GREEN AND CLEAN” (see Fig. 12.10).
If the sides of the wall are 15 m, 11 m and 6 m, find
the area painted in colour.
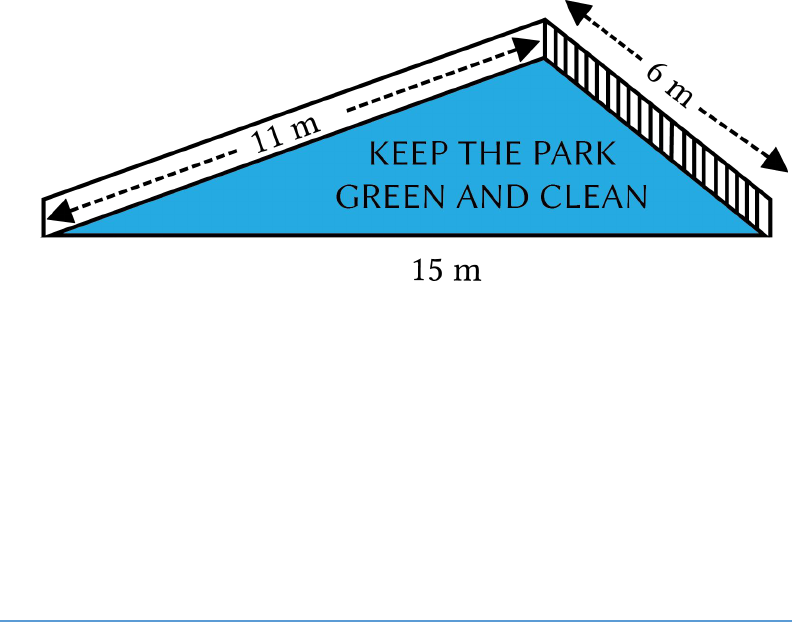
Fig. 12.10
Solution
The sides of the triangular wall are 15 m, 11 m and 6
m.
Hence, the semi perimeter of the triangular
wall
m m( )15 11 6 / 2 16
16 s
By Heron's formula,
the area painted=

2
2
2
2
16(16 15)(16 11)(16 6)
16 1 5 10 m
800 m
20 m
s s a s b s c
Question: 4
Find the area of a triangle two sides of which
are 18 cm and 10 cm and the perimeter is 42 cm.
Solution
The perimeter of the triangle
42
cm
The two sides of the triangle
18
cm and 10 cm.
Hence, the third side of the triangle
cm cm.( )42 18 10 14
The semi perimeter of the triangle
cm
42
21
2
cm21 s
By Heron's formula,
Area of the triangle =

2
2
3 7
21 11
s s a s b s c
21(21 18)(21 10)(21 14)
21 11 cm
cm
Question: 5
Sides of a triangle are in the ratio of
12:17: 25
and
its perimeter is 540 cm. Find its area.
Solution
Ratio of the sides of the triangle
12:17: 25
.
Let the common ratio be x, then the sides of the
triangle will be
12 , 17x x
and
25 ,x
The perimeter of the triangle
540
cm.
cm12 17 25 540x x x
cm54 540x
10x
cm
Hence, the sides of the triangle will be,
cm12 12 10 120x
cm17 17 10 170x
cm25 25 10 250x
The semi perimeter of triangle
540/ 2 270
cm.
270 cms
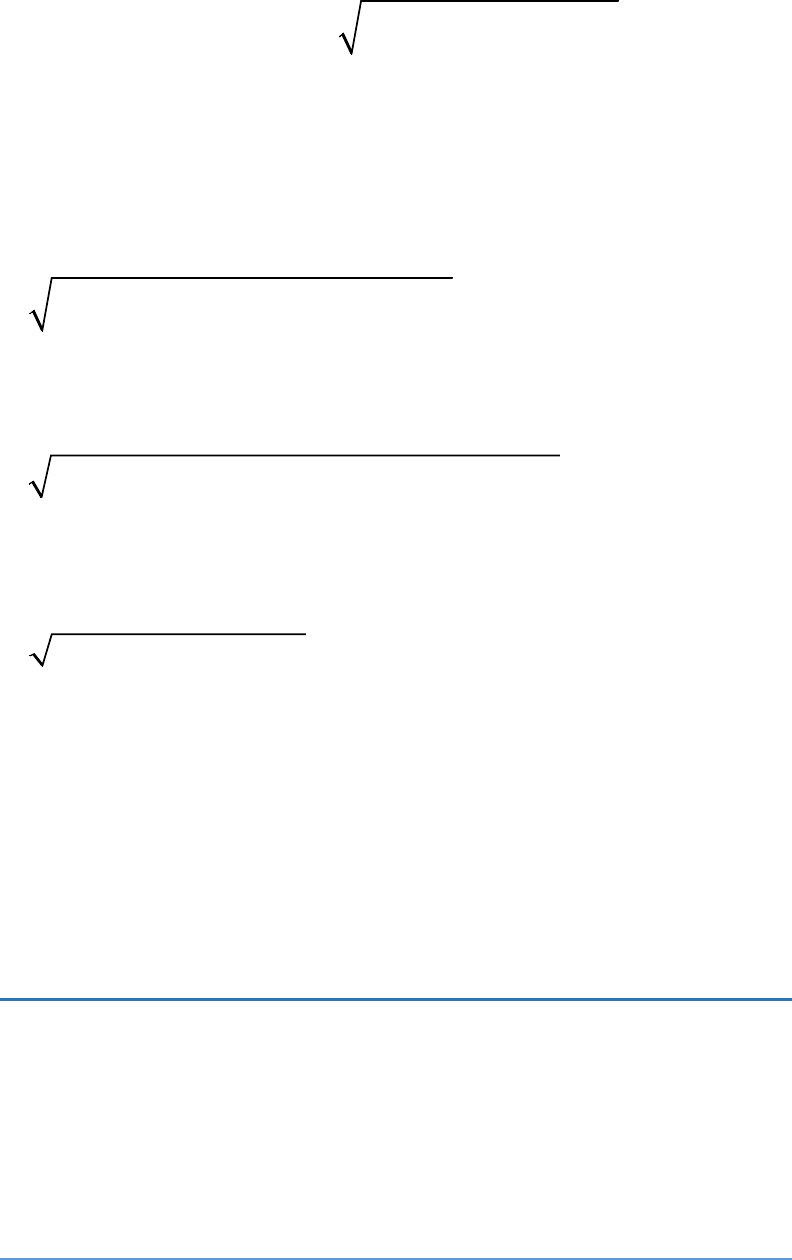
By Heron's formula,
Area of the triangle =
s s a s b s c
270 270 270 270a b c
120 270(270 )(270 170)(270 250)
2
270 150 100 20 cm
2
cm9000
Question :6
An isosceles triangle has perimeter 30 cm and each of
the equal sides is 12 cm. Find the area of the triangle.
Solution

The length of the equal sides of the isosceles triangle
cm12
The perimeter of the triangle
cm.30
Hence, the length of the third side
cm cm30 12 12) 6(
The semi perimeter of the triangle
cm cm30/ 2 15
cm15 s
By Heron's formula,
Area of the triangle =
s s a s b s c
15 15 12 15 12 15 6
2
cm15 3 3 9
2
cm9 15

Exercise 12.2
Question: 1
A park, in the shape of a quadrilateral ABCD, has
m90º, 9 ,C AB
m m12 , 5BC CD
and
m8AD
. How much area does it occupy?
Solution
Given,
m90º, 9 ,C AB
m m12 , 5BC CD
and
m8 .AD
Let us join BD.
Now, in ΔBCD,
2 2 2
BD BC CD
(Pythagoras theorem)
2 2 2
12 5BD
2
169BD
m13BD

Area of
m
2
1/ 2 12 5 30BCD
Now,
Semi perimeter of ΔABD (s)
m m m(8 9 13 / 2 3) 0/ 2 15
m15s
Using Heron's formula,
Area of ΔABD =
s s a s b s c
15 15 13 15 9 15 8
2
2 6 7 m15
2
m6 35
2
m (approx.)35.5

Hence, the area of the quadrilateral ABCD = Area of
ΔBCD + Area of
m m m
2 2 2
30 35.5 65.5 ABD
Question: 2
Find the area of a quadrilateral ABCD in which AB =
3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC =
5 cm.

Solution
The sides of the quadrilateral ABCD are,
AB = 3 cm, BC = 4 cm, CD = 4 cm, and DA = 5 cm.
The diagonal AC = 5 cm.
Now, in ΔABC,
2 2 2
AC AB BC
(Pythagoras theorem).
2 2 2
5 3 4
25 25
Hence, ΔABC is a right angled at B.
∴ Area of ΔABC = 1/2 × 3 × 4 = 6 cm
2
Now,
The semi perimeter of ΔACD ,s = (5 + 5 + 4)/2 cm =
14/2 cm = 7 cm

cm7 s
By Heron's formula,
Area of ΔACD =
2
2
2
5 4
7 2 2 3
cm
cm
cm (approx.)
7 7 5 7 7
2 21
9.17
s s a s b s c
Hence, the area of the quadrilateral ABCD = Area of
ΔABC + Area of ΔACD = 6 cm
2
+ 9.17 cm
2
= 15.17
cm
2
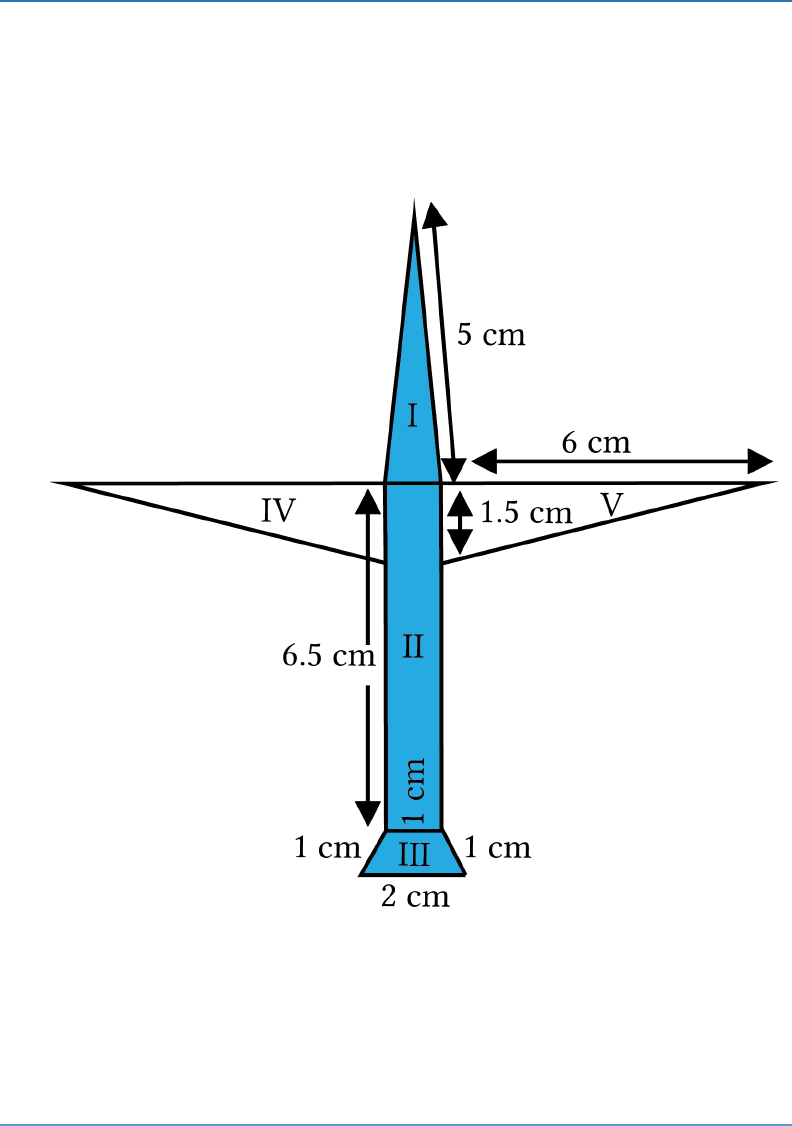
Question: 3
Radha made a picture of an airplane with coloured
paper as shown in Fig 12.15. Find the total area of the
paper used.
Fig 12.15
Solution
As shown in the figure, there are five sections in the
picture of the aeroplane. Hence, the total area will be
sum of the areas of the five sections.
Now,
The length of the sides of the triangle in section I are
5 cm, 1 cm and 5 cm.
The perimeter of the triangle = 5 + 5 + 1 = 11 cm.
The semi perimeter = 11/2 cm = 5.5 cm
cm5.5 s
By Heron's formula,
Area of section I =
2
2
2
2
5 1
5.5 0.5 0.5 4.5
0.75 3.317
2.488 ( )
cm
cm
cm
cm approx.
5.5 5.5 5 5.5 5.5
0.75 11
s s a s b s c
The lengths of the sides of the rectangle of section II
are 6.5 cm and 1 cm.
Hence, the area of section II = 6.5 × 1 = 6.5 cm
2
.
Section III is an isosceles trapezium which is divided
into three equilateral triangles of side 1 cm each.
Hence, the area of the trapezium = 3 × √3/4 ×
1
2
cm
2
= 1.3 cm
2
(approx)
Section IV and V are 2 congruent right angled
triangles with base 6 cm and height 1.5 cm.
Area of the region IV and V = 2 × 1/2 × 6 × 1.5
cm
2
= 9 cm
2

Hence, the total area of the paper = (2.488 + 6.5 + 1.3
+ 9) cm
2
= 19.3 cm
2
Question: 4
A triangle and a parallelogram have the same base and
the same area. If the sides of the triangle are 26 cm, 28
cm and 30 cm, and the parallelogram stands on the
base 28 cm, find the height of the parallelogram.
Solution
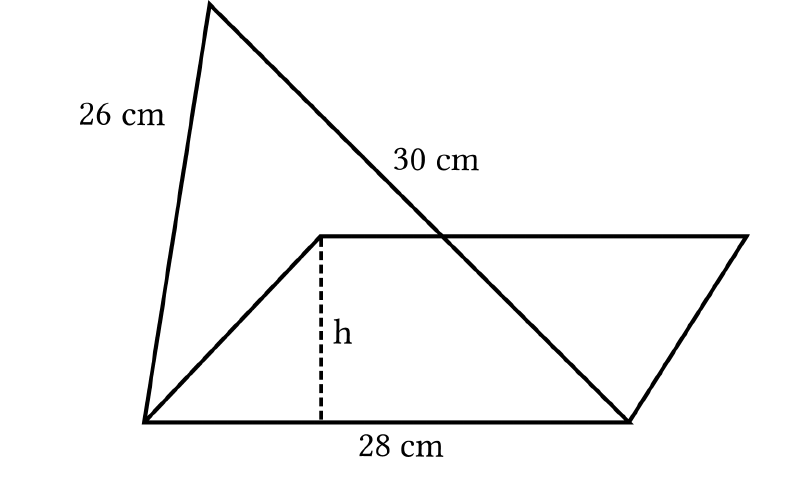
The lengths of the sides of the triangles are 26 cm, 28
cm and 30 cm.
The perimeter of the triangle = 26 + 28 + 30 = 84 cm.
The semi perimeter of the triangle = 84/2 cm = 42 cm

42 cm s
By Heron's formula,
Area of the triangle =
2
2
26 28 30
16 14 12
s s a s b s c
42 42 42 42
42
336
cm
cm
Let the height of parallelogram be h.
Area of the parallelogram and area of the triangle are
equal.
⟹ Area of parallelogram = Area of triangle
28 cm × h = 336 cm
2

⟹ h = 336/28 cm
⟹ h = 12 cm
Hence, the height of the parallelogram is 12 cm.
Question: 5
A rhombus shaped field has green grass for 18 cows to
graze. If each side of the rhombus is 30 m and its
longer diagonal is 48 m, how much area of grass field
will each cow be getting?
Solution
Let the rhombus be ABCD, with sides AB, BC, CD and
DA.
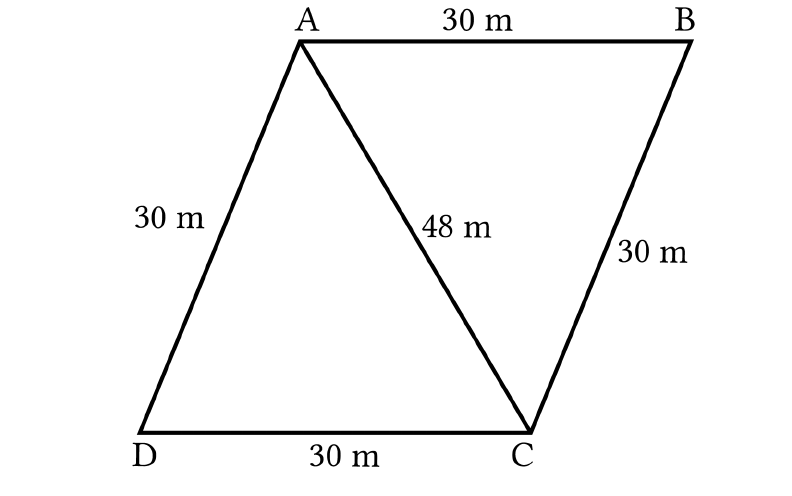
The diagonal AC divides the rhombus ABCD into two
congruent triangles of equal area.
The semi perimeter of ΔABC = (30 + 30 + 48)/2 m =
54 m
54 m s
By Heron's formula,
Area of the ΔABC =
2
2
30 30 48
14 14 6
252
s s a s b s c
54 54 54 54
54
m
m
Thus, the area of field = 2 × area of the ΔABC = (2 ×
252) m
2
= 504 m
2
Hence, the area of the grass field each cow will get =
504/18 m
2
= 28 m
2
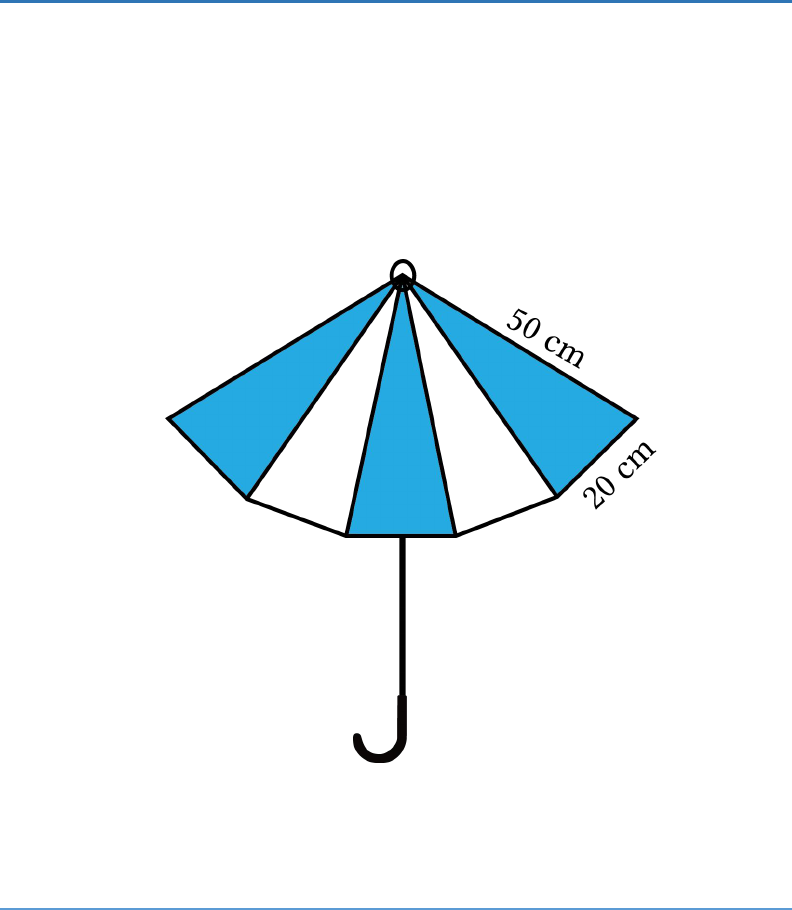
Question: 6
An umbrella is made by stitching 10 triangular pieces
of cloth of two different colours (see Fig.12.16), each
piece measuring 20 cm, 50 cm and 50 cm. How much
cloth of each colour is required for the umbrella?
Fig.12.16
Solution
The lengths of the sides of the triangle are 20 cm, 50
cm and 50 cm.

Thus, the semi perimeter of each triangular piece, s =
(50 + 50 + 20)/2 cm = 120/2 cm = 60 cm.
By Heron's formula,
the area of the triangular piece =
2
2
50 50 20
10 10 40
200
cm
cm
60 60 60 60
60
6
s s a s b s c

∴ The area of the triangular piece of one colour= 5 ×
200√6 cm
2
= 1000√6 cm
2
Hence, 1000√6 cm
2
cloth of each colour is required for
the umbrella.
Question: 7
A kite in the shape of a square with a diagonal 32 cm
and an isosceles triangle of base 8 cm and sides 6 cm
each is to be made of three different shades as shown
in Fig. 12.17. How much paper of each shade has been
used in it?
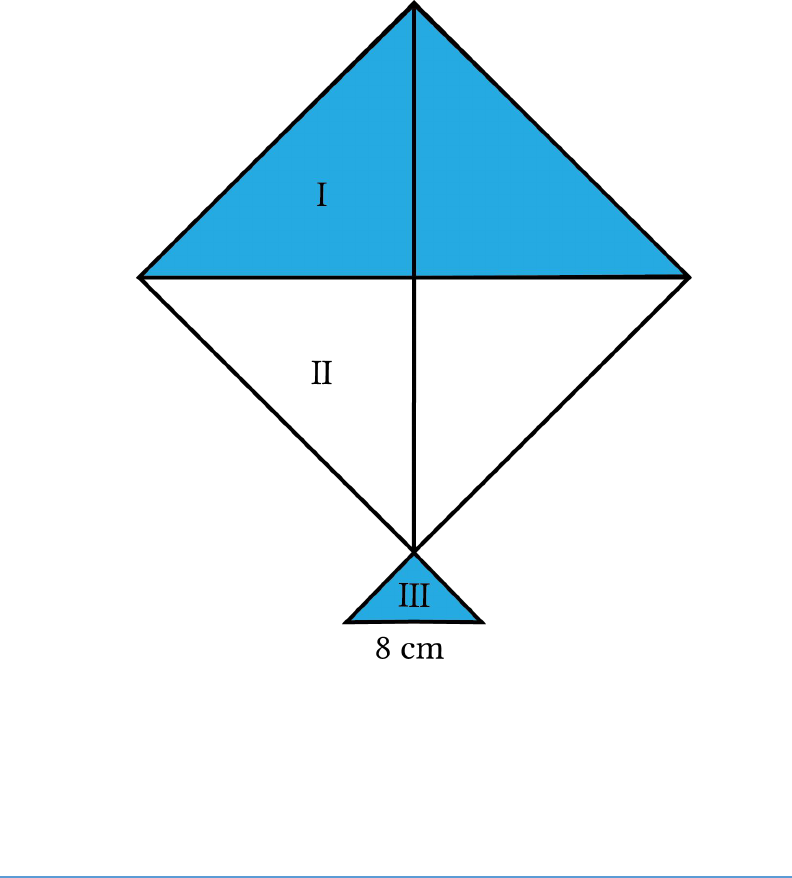
Fig.
12.17
Solution
Diagonals of a square bisect each other at right angle.
Hence, the area of the square = 1/2 (diagonal)
2
= 1/2 × 32 × 32 = 512 cm
2
∵ Area of shade I = Area of shade II
⟹ 512/2 cm
2
= 256 cm
2

So, the area of paper required in each shade = 256
cm
2
For III section,
The length of the sides of the triangle are 6 cm, 6 cm
and 8 cm.
The semi perimeter of the triangle =
(6 )6
2
8
cm =
10 cm

10 cm s
By Heron's formula,
Area of the III triangular pieces =
2
2
6 6 8
4 4 2
8 5
s s a s b s c
10 10 10 10
10
cm
cm
Question: 8
A floral design on a floor is made up of 16 tiles which
are triangular, the sides of the triangle being 9 cm, 28
cm and 35 cm (see Fig. 12.18). Find the cost of
polishing the tiles at the rate of 50p per cm
2
.

Fig. 12.18
Solution
The lengths of the sides of the triangles are 9 cm, 28
cm and 35 cm.

The semi perimeter of each triangular shape = (28 + 9
+ 35)/2 cm = 36 cm
36 s cm
Using Heron's formula,
the area of each triangular shape =
2
2
2
28 9 35
8 27 1
36
88.2
cm
cm
cm
36 36 36 36
36
6
s s a s b s c

Thus, the total area of 16 tiles
cm
2
16 88.2 1411.2
cm
2
.
Cost of polishing the tiles = 50p per cm
2
Hence, the total cost of polishing the tiles = Rs
(1411.2 × 0.5) = Rs 705.6
Question: 9
A field is in the shape of a trapezium whose parallel
sides are 25 m and 10 m long. The non-parallel sides
are 14 m and 13 m. Find the area of the field.
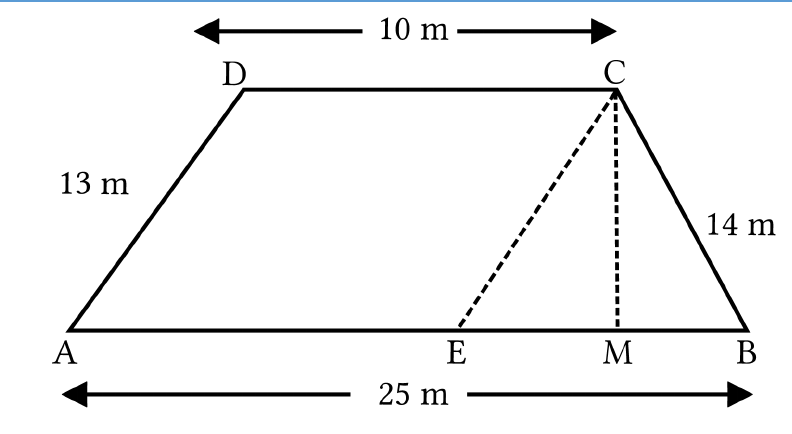
Solution
Let ABCD be the given trapezium with the parallel
sides as 25 m and 10 m and the non-parallel sides as
14 m and 13 m as shown in the figure above.
Let the parallel sides are AB = 25 m and CD = 10 m
and the non-parallel sides are AD = 13 m and BC =
14 m.
We draw a perpendicular line from vertex C to AB
such that CM ⊥ AB. Also, draw a line parallel to AD
from point C such that it intersects AB at point E.
Now, in ΔBCE,
BC = 14 m, CE = AD = 13 m and
m25 10 15 .BE AB AE
The semi perimeter of the ΔBCE =
15 13( )
2
14
=
21 m
21 ms
By Heron's formula,
Area of the ΔBCE =
2
2
14 13 15
7 8 6
84
m
m
21 21 21 21
21
s s a s b s c
Also, the area of the
m
2
1
84
2
BCE BE CM
m
2
1
15 84
2
CM
m
2
168
15
CM
m
2
56
5
CM
Area of the parallelogram AECD = Base × Altitude

m
2
56
10 112
5
AE CM
Area of the trapezium ABCD = Area of AECD + Area
of ΔBCE
(112 + 84) m
2
= 196 m
2