Rainbow Coloring Graph Theory
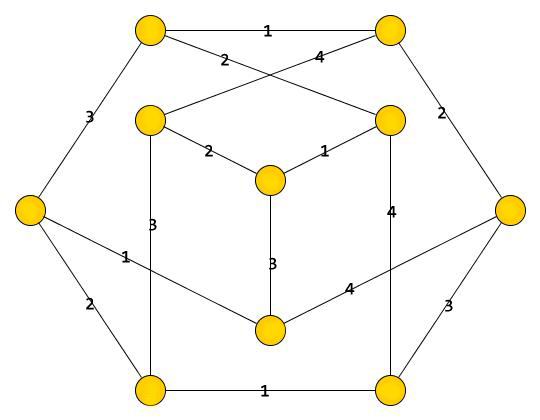
Rainbow coloring of a wheel graph, with three colors. Every two non-adjacent vertices can be connected by a rainbow path, either directly through the center vertex (bottom left) or by detouring around one triangle to avoid a repeated edge color (bottom right). In graph theory, a path in an edge.

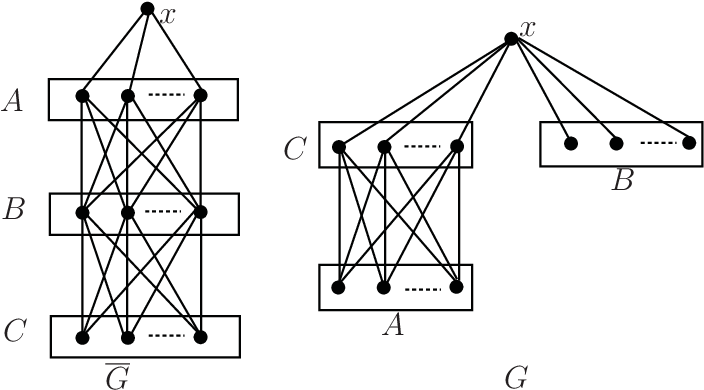
This then results in a vertex coloring of the graph, often called a rainbow coloring since all vertex colors are distinct. Here, we consider edge colorings of graphs with positive integers such that each vertex color is the average of the colors of its incident edges and all vertex colors are distinct. First get a rainbow coloring of the connected dominating set.

The total rainbow coloring of graph C 4 C 4 | Download Scientific Diagram
Then color the remaining edges in such a way that for each vertex x outside there are two disjoint rainbow colored paths (rainbow colored using different set of colors). Rainbow Connections of Graphs covers this new and emerging topic in graph theory and brings together a majority of the results that deal with the concept of rainbow connections, first introduced by Chartrand et al. in 2006.

The authors begin with an introduction to rainbow connectedness, rainbow coloring, and rainbow connection number. Graph coloring problem and problem on the existence of paths and cycles have always been popular topics in graph theory. The problem on the existence of rainbow paths and rainbow cycles in edge colored graphs, as an integration of them, was well studied for a long period.
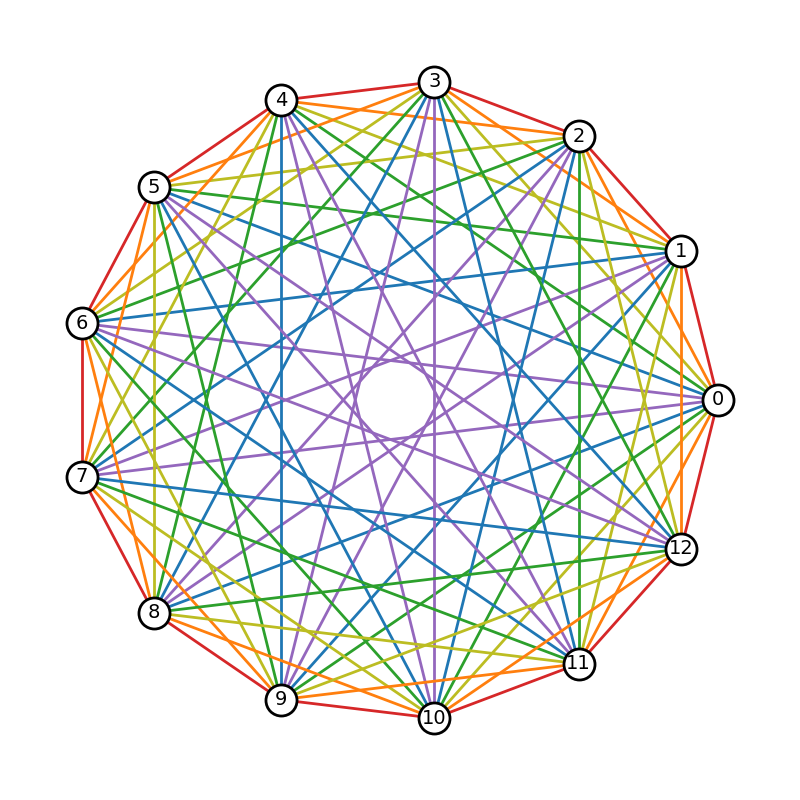
Example of 2-local strong rainbow coloring on prism graph í µí± 5 × í ...
3) Online Rainbow Coloring: In online rainbow coloring, the inputs are a non-trivial un-directed connected simple graph G and a set of colors c. The output is a rainbow colored graph, where there must be atleast one rainbow path between every distinct pair of vertices. Our goal is to use minimum colors while making G rainbow colored.

We have constraints such as the edges of G are unknown at. Assistant Professor / Department of Mathematics Sathyabama University, Chennai, India Abstract-A rainbow coloring of a connected graph is a coloring of the edges of the graph, such that every pair of vertices is connected by at least one path in which no two edges are colored the same. Computing the rainbow connection number of a graph is NP.

Rainbow Graph Designs Hung-Lin Fu (傅 恒 霖) - ppt download
An edge color graph G edge- related some two vertices linked different colors. Obviously, graph colourful edge concurrent emotionally concerned. Chapter deals discipline graph theory known diagram coloring.
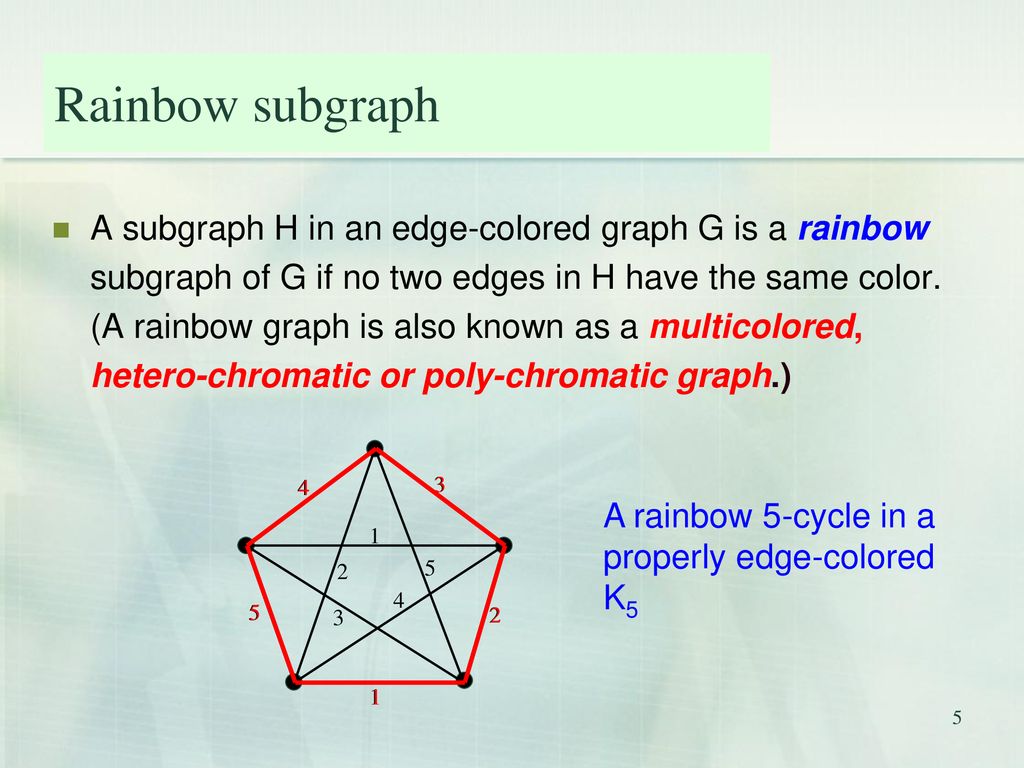
However, some definitions basic concepts graph hypothesis required. A rainbow graph is a graph that admits a vertex. The graph is rainbow vertex-connected if there is a rainbow vertex path between every pair of its vertices.

In the Rainbow Vertex Coloring (RVC) problem we want to decide whether the vertices of a given graph can be colored with at mostkcolors so that the graph becomes rainbow vertex.