{
"cells": [
{
"cell_type": "markdown",
"metadata": {
"id": "_jQ1tEQCxwRx"
},
"source": [
"##### Copyright 2019 The TensorFlow Authors."
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"cellView": "form",
"execution": {
"iopub.execute_input": "2020-09-23T04:26:04.331418Z",
"iopub.status.busy": "2020-09-23T04:26:04.330777Z",
"iopub.status.idle": "2020-09-23T04:26:04.332870Z",
"shell.execute_reply": "2020-09-23T04:26:04.333279Z"
},
"id": "V_sgB_5dx1f1"
},
"outputs": [],
"source": [
"#@title Licensed under the Apache License, Version 2.0 (the \"License\");\n",
"# you may not use this file except in compliance with the License.\n",
"# You may obtain a copy of the License at\n",
"#\n",
"# https://www.apache.org/licenses/LICENSE-2.0\n",
"#\n",
"# Unless required by applicable law or agreed to in writing, software\n",
"# distributed under the License is distributed on an \"AS IS\" BASIS,\n",
"# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.\n",
"# See the License for the specific language governing permissions and\n",
"# limitations under the License."
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "rF2x3qooyBTI"
},
"source": [
"# 심층 합성곱 생성적 적대 신경망"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "0TD5ZrvEMbhZ"
},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "bBxnTS5bBk2d"
},
"source": [
"Note: 이 문서는 텐서플로 커뮤니티에서 번역했습니다. 커뮤니티 번역 활동의 특성상 정확한 번역과 최신 내용을 반영하기 위해 노력함에도\n",
"불구하고 [공식 영문 문서](https://www.tensorflow.org/?hl=en)의 내용과 일치하지 않을 수 있습니다.\n",
"이 번역에 개선할 부분이 있다면\n",
"[tensorflow/docs-l10n](https://github.com/tensorflow/docs-l10n/) 깃헙 저장소로 풀 리퀘스트를 보내주시기 바랍니다.\n",
"문서 번역이나 리뷰에 참여하려면\n",
"[docs-ko@tensorflow.org](https://groups.google.com/a/tensorflow.org/forum/#!forum/docs-ko)로\n",
"메일을 보내주시기 바랍니다."
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "ITZuApL56Mny"
},
"source": [
"이 튜토리얼은 [심층 합성곱 생성적 적대 신경망](https://arxiv.org/pdf/1511.06434.pdf) (Deep Convolutional Generative Adversarial Networks, DCGAN)을 이용하여, 손으로 쓴 숫자들을 어떻게 생성할 수 있는지 보여줍니다. 이 코드는 [케라스 Sequential API](https://www.tensorflow.org/guide/keras)와 `tf.GradientTape` 훈련 루프를 사용하여 작성됐습니다."
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "2MbKJY38Puy9"
},
"source": [
"## 생성적 적대 신경망(GANs)은 무엇인가요? \n",
"\n",
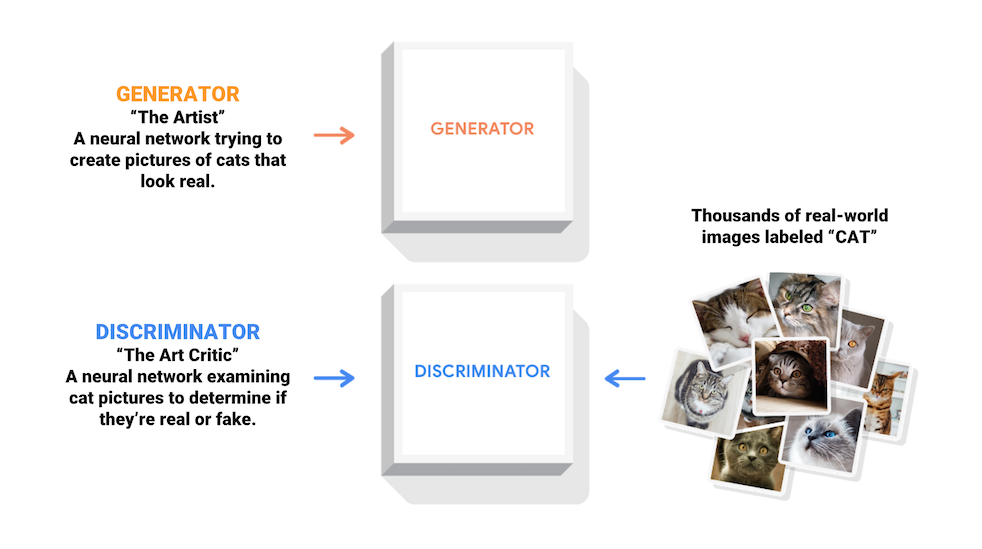
"[생성적 적대 신경망](https://arxiv.org/abs/1406.2661) (Generative Adversarial Networks, GANs)은 요즘 컴퓨터 과학에서 가장 흥미로운 아이디어 중 하나입니다. 두개의 모델이 적대적인 과정을 통해 동시에 훈련됩니다. *생성자* (\"예술가\")는 진짜처럼 보이는 이미지를 생성하도록 배우는 와중에, *감별자* (\"예술비평가\")는 가짜의 이미지로부터 진짜를 구별하게 되는 것을 배우게 됩니다.\n",
"\n",
"\n",
"\n",
"\n",
"\n",
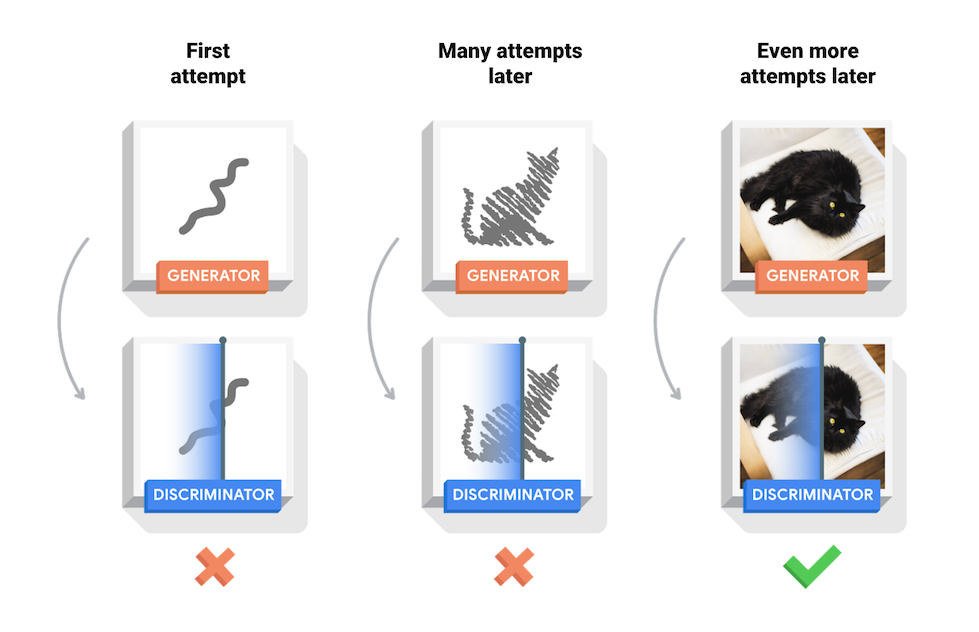
"훈련과정 동안 *생성자*는 점차 실제같은 이미지를 더 잘 생성하게 되고, *감별자*는 점차 진짜와 가짜를 더 잘 구별하게됩니다. 이 과정은 *감별자*가 가짜 이미지에서 진짜 이미지를 더이상 구별하지 못하게 될때, 평형상태에 도달하게 됩니다. \n",
"\n",
"\n",
"\n",
"이 노트북은 이 과정을 MNIST 데이터를 이용하여 보여줍니다. 아래의 애니메이션은 50 에포크(epoch)동안 훈련한 *생성자*가 생성해낸 연속된 이미지들을 보여줍니다. 이미지들은 랜덤한 잡음으로 부터 시작되었고, 점차 시간이 지남에 따라 손으로 쓴 숫자들을 닮아가게 됩니다.\n",
"\n",
"\n",
"\n",
"생성적 적대 신경망 (GANs)에 대해 더 배우고 싶으시다면, MIT의 [Intro to Deep Learning](http://introtodeeplearning.com/) 수업을 추천합니다."
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "e1_Y75QXJS6h"
},
"source": [
"### 텐서플로와 다른 라이브러리 불러오기"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"execution": {
"iopub.execute_input": "2020-09-23T04:26:04.341114Z",
"iopub.status.busy": "2020-09-23T04:26:04.337837Z",
"iopub.status.idle": "2020-09-23T04:26:23.740835Z",
"shell.execute_reply": "2020-09-23T04:26:23.740081Z"
},
"id": "g5RstiiB8V-z"
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"\u001b[33mWARNING: You are using pip version 20.2.2; however, version 20.2.3 is available.\r\n",
"You should consider upgrading via the '/tmpfs/src/tf_docs_env/bin/python -m pip install --upgrade pip' command.\u001b[0m\r\n"
]
}
],
"source": [
"!pip install -q tensorflow-gpu==2.0.0-rc1"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"execution": {
"iopub.execute_input": "2020-09-23T04:26:23.745753Z",
"iopub.status.busy": "2020-09-23T04:26:23.745066Z",
"iopub.status.idle": "2020-09-23T04:26:32.715464Z",
"shell.execute_reply": "2020-09-23T04:26:32.714716Z"
},
"id": "WZKbyU2-AiY-"
},
"outputs": [],
"source": [
"import tensorflow as tf"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"execution": {
"iopub.execute_input": "2020-09-23T04:26:32.725466Z",
"iopub.status.busy": "2020-09-23T04:26:32.724693Z",
"iopub.status.idle": "2020-09-23T04:26:32.728263Z",
"shell.execute_reply": "2020-09-23T04:26:32.728781Z"
},
"id": "wx-zNbLqB4K8"
},
"outputs": [
{
"data": {
"text/plain": [
"'2.0.0-rc1'"
]
},
"execution_count": 1,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"tf.__version__"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"execution": {
"iopub.execute_input": "2020-09-23T04:26:32.738090Z",
"iopub.status.busy": "2020-09-23T04:26:32.737422Z",
"iopub.status.idle": "2020-09-23T04:26:34.140204Z",
"shell.execute_reply": "2020-09-23T04:26:34.139513Z"
},
"id": "YzTlj4YdCip_"
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"\u001b[33mWARNING: You are using pip version 20.2.2; however, version 20.2.3 is available.\r\n",
"You should consider upgrading via the '/tmpfs/src/tf_docs_env/bin/python -m pip install --upgrade pip' command.\u001b[0m\r\n"
]
}
],
"source": [
"# GIF를 만들기위해 설치합니다.\n",
"!pip install -q imageio"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"execution": {
"iopub.execute_input": "2020-09-23T04:26:34.145939Z",
"iopub.status.busy": "2020-09-23T04:26:34.145216Z",
"iopub.status.idle": "2020-09-23T04:26:34.436384Z",
"shell.execute_reply": "2020-09-23T04:26:34.435709Z"
},
"id": "YfIk2es3hJEd"
},
"outputs": [],
"source": [
"import glob\n",
"import imageio\n",
"import matplotlib.pyplot as plt\n",
"import numpy as np\n",
"import os\n",
"import PIL\n",
"from tensorflow.keras import layers\n",
"import time\n",
"\n",
"from IPython import display"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "iYn4MdZnKCey"
},
"source": [
"### 데이터셋 로딩 및 준비\n",
"생성자와 감별자를 훈련하기위해 MNIST 데이터셋을 사용할것입니다. 생성자는 손글씨 숫자 데이터를 닮은 숫자들을 생성할 것입니다. "
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"execution": {
"iopub.execute_input": "2020-09-23T04:26:34.441250Z",
"iopub.status.busy": "2020-09-23T04:26:34.440575Z",
"iopub.status.idle": "2020-09-23T04:26:34.758688Z",
"shell.execute_reply": "2020-09-23T04:26:34.759207Z"
},
"id": "a4fYMGxGhrna"
},
"outputs": [],
"source": [
"(train_images, train_labels), (_, _) = tf.keras.datasets.mnist.load_data()"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"execution": {
"iopub.execute_input": "2020-09-23T04:26:34.764177Z",
"iopub.status.busy": "2020-09-23T04:26:34.763387Z",
"iopub.status.idle": "2020-09-23T04:26:34.898240Z",
"shell.execute_reply": "2020-09-23T04:26:34.897497Z"
},
"id": "NFC2ghIdiZYE"
},
"outputs": [],
"source": [
"train_images = train_images.reshape(train_images.shape[0], 28, 28, 1).astype('float32')\n",
"train_images = (train_images - 127.5) / 127.5 # 이미지를 [-1, 1]로 정규화합니다."
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"execution": {
"iopub.execute_input": "2020-09-23T04:26:34.902788Z",
"iopub.status.busy": "2020-09-23T04:26:34.902011Z",
"iopub.status.idle": "2020-09-23T04:26:34.904554Z",
"shell.execute_reply": "2020-09-23T04:26:34.903824Z"
},
"id": "S4PIDhoDLbsZ"
},
"outputs": [],
"source": [
"BUFFER_SIZE = 60000\n",
"BATCH_SIZE = 256"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"execution": {
"iopub.execute_input": "2020-09-23T04:26:35.900138Z",
"iopub.status.busy": "2020-09-23T04:26:35.746732Z",
"iopub.status.idle": "2020-09-23T04:26:35.903975Z",
"shell.execute_reply": "2020-09-23T04:26:35.903334Z"
},
"id": "-yKCCQOoJ7cn"
},
"outputs": [],
"source": [
"# 데이터 배치를 만들고 섞습니다.\n",
"train_dataset = tf.data.Dataset.from_tensor_slices(train_images).shuffle(BUFFER_SIZE).batch(BATCH_SIZE)"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "THY-sZMiQ4UV"
},
"source": [
"## 모델 만들기 \n",
"생성자와 감별자는 [케라스 Sequential API](https://www.tensorflow.org/guide/keras#sequential_model)를 이용해 정의됩니다. "
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "-tEyxE-GMC48"
},
"source": [
"### 생성자\n",
"\n",
"생성자는 시드값 (seed; 랜덤한 잡음)으로부터 이미지를 생성하기 위해, `tf.keras.layers.Conv2DTranspose` (업샘플링) 층을 이용합니다. 처음 `Dense`층은 이 시드값을 인풋으로 받습니다. 그 다음 원하는 사이즈 28x28x1의 이미지가 나오도록 업샘플링을 여러번 합니다. tanh를 사용하는 마지막 층을 제외한 나머지 각 층마다 활성함수로 `tf.keras.layers.LeakyReLU`을 사용하고 있음을 주목합시다."
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"execution": {
"iopub.execute_input": "2020-09-23T04:26:35.914564Z",
"iopub.status.busy": "2020-09-23T04:26:35.913743Z",
"iopub.status.idle": "2020-09-23T04:26:35.916165Z",
"shell.execute_reply": "2020-09-23T04:26:35.915647Z"
},
"id": "6bpTcDqoLWjY"
},
"outputs": [],
"source": [
"def make_generator_model():\n",
" model = tf.keras.Sequential()\n",
" model.add(layers.Dense(7*7*256, use_bias=False, input_shape=(100,)))\n",
" model.add(layers.BatchNormalization())\n",
" model.add(layers.LeakyReLU())\n",
"\n",
" model.add(layers.Reshape((7, 7, 256)))\n",
" assert model.output_shape == (None, 7, 7, 256) # 주목: 배치사이즈로 None이 주어집니다.\n",
"\n",
" model.add(layers.Conv2DTranspose(128, (5, 5), strides=(1, 1), padding='same', use_bias=False))\n",
" assert model.output_shape == (None, 7, 7, 128)\n",
" model.add(layers.BatchNormalization())\n",
" model.add(layers.LeakyReLU())\n",
"\n",
" model.add(layers.Conv2DTranspose(64, (5, 5), strides=(2, 2), padding='same', use_bias=False))\n",
" assert model.output_shape == (None, 14, 14, 64)\n",
" model.add(layers.BatchNormalization())\n",
" model.add(layers.LeakyReLU())\n",
"\n",
" model.add(layers.Conv2DTranspose(1, (5, 5), strides=(2, 2), padding='same', use_bias=False, activation='tanh'))\n",
" assert model.output_shape == (None, 28, 28, 1)\n",
"\n",
" return model"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "GyWgG09LCSJl"
},
"source": [
"(아직 훈련이 되지않은) 생성자를 이용해 이미지를 생성해봅시다. "
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"execution": {
"iopub.execute_input": "2020-09-23T04:26:35.928749Z",
"iopub.status.busy": "2020-09-23T04:26:35.927907Z",
"iopub.status.idle": "2020-09-23T04:26:36.310399Z",
"shell.execute_reply": "2020-09-23T04:26:36.310945Z"
},
"id": "gl7jcC7TdPTG"
},
"outputs": [
{
"data": {
"text/plain": [
""
]
},
"execution_count": 1,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAPsAAAD4CAYAAAAq5pAIAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAYT0lEQVR4nO2de4yV5bXGn8UwIPeL3IYBBME7IMiAtqjBEtGaFtC2RpMSNUZML7FNGs+xmLQ2bRPj0WPbaNrgkXqrtLVSNdYe8SBWvCFT5A4iCgjDZVCQi9yHdf6Y7Qm18z5rOpe9J+d9fslkZvYza3/vfHs/8+3Z611rmbtDCPH/n3alXoAQojjI7EJkgswuRCbI7EJkgswuRCa0L+bBOnfu7D179kzqZkbjmR5lFaL7bk58FFtXV9fk+waAsrIyqp84caLJsUePHqV6eXl5s+Lbt08/xaLzxmIB/ntHRI9J9HsfP368yceOiB4zduy9e/fi0KFDDT6hmmV2M7sSwC8BlAH4L3e/m/18z549cfPNNyf1jh070uN16NAhqUUnP3riHDlyhOpsbdGxd+/eTXX2ewH1541x8ODBpNa1a1cau2XLFqpXVlZS/cMPP6R6nz59klp0zvv27Uv1Tz/9lOrsj+j+/fubdezoMY3+ELVrl35R3a1btyYf+/HHH08fk94rwczKADwI4MsAzgVwvZmd29T7E0K0Ls35n30CgA3u/oG7HwXwewDTWmZZQoiWpjlmrwRw8mvArYXb/gEzm2lm1WZWHb3sEkK0Hq3+bry7z3b3Knev6tKlS2sfTgiRoDlmrwEw+KTvBxVuE0K0QZpj9iUAzjCzYWbWAcB1AJ5rmWUJIVqaJqfe3P24mX0XwIuoT73NcffVLKa8vByDBw9O6hs2bKDHZGmkHj160Ni9e/dSPUq1bNq0qcmxAwYMoHqU/jrllFOozs5L9K/T4cOHqX7gwAGqDxw4kOr9+/dPap07d6axGzdupHq0P4Gl/QYNGkRj9+3b1+T7BuJ07JAhQ5JabW0tjWWpOZbGbVae3d1fAPBCc+5DCFEctF1WiEyQ2YXIBJldiEyQ2YXIBJldiEyQ2YXIhKLWsx85cgTvv/9+Uo/ypizXHZWJjhw5kuqrV9MtAvjoo4+SWpSrjnKyw4cPp/qaNWuozs7pqFGjaCzb9wAAb7zxBtVZHh3gdeNRGeiyZcuoXlFRQfVOnToltWPHjtHYdevWUT3i4osvpvqOHTuSWvRcZD45dOhQUtOVXYhMkNmFyASZXYhMkNmFyASZXYhMkNmFyISipt7at2+PU089NalHbatGjBiR1KJUyp49e6j+la98hervvvtuUovKIaOWyZEepeZYOWV0XqIS1aFDh1I96trbvXv3pBal7aIy0Si+pibdS2X06NE0tl+/flSPyo6jdCxLebL0GQBs3ryZ6il0ZRciE2R2ITJBZhciE2R2ITJBZhciE2R2ITJBZhciE4qaZz9x4gSdnhnl2T/55JOkFpXHRqWc77zzDtXXr1+f1KKc64QJE6j++uuvU/2iiy6i+rhx45Larl27aOz8+fOpPn78eKqz0l+AT0t94oknaOwVV1xBdVYmCvDSYjbtFIjbf0d6tPeCTb+95JJLmnzfbN+DruxCZILMLkQmyOxCZILMLkQmyOxCZILMLkQmyOxCZEJR8+zt2rWj44XPOussGn/06NGkFo09HjZsGNW3bdtG9bFjxya1jh070liWUwWAiRMnUv29996jOvvdysvLaeztt99O9Wjt7LwAvC1y1OY6asEd5eEfe+yxpBaNbJ4yZQrVo/be0f6Gb3/720lt+fLlNJbVyrP23M0yu5ltArAfQB2A4+5e1Zz7E0K0Hi1xZb/M3fk2KiFEydH/7EJkQnPN7gDmm9nfzWxmQz9gZjPNrNrMqqO970KI1qO5L+MvdvcaM+sH4CUzW+fur578A+4+G8BsABg0aBDvrCiEaDWadWV395rC51oAfwbAy7uEECWjyWY3sy5m1u2zrwFMAbCqpRYmhGhZmvMyvj+APxfqyNsDeNLd/5sF1NXVYe/evUk9GtHbt2/fpLZz504aG9WcR73bWQ/yaMRuVM8e9QFftGgR1Vmdf7S/4K9//SvVo98tun+2tmhvRNSD4L777qN67969k1qvXr1o7PPPP091tucDiJ9vTz75ZFJj6wb4KOp27dLX7yab3d0/AHB+U+OFEMVFqTchMkFmFyITZHYhMkFmFyITZHYhMqHoI5tZ+oyN9wWATZs2JbVJkybR2Ki1b48ePah+xhlnJLUuXbrQ2MrKSqqzdCQATJ48meqs9XDUMnnMmDFUHzJkCNWjcdJs1PVtt91GY9etW0f1aMw2Kw2OWmRH6c6RI0dS/ZlnnqE6Gzd93nnn0dgDBw4kNZby05VdiEyQ2YXIBJldiEyQ2YXIBJldiEyQ2YXIBJldiEwoap69rq6OljxG+eYzzzwzqUWte6McfjT+l43CjcY9R7no3bt3U72uro7qf/nLX5JaVII6d+5cqn/jG9+g+scff0z1s88+O6nNmjWLxkb55mjvRFVVutnxww8/TGOjPPqxY8eoHo3Zfuqpp5JaVG7Nyo6Zh3RlFyITZHYhMkFmFyITZHYhMkFmFyITZHYhMkFmFyITij6ymdXbDhgwgMbv378/qR08eJDGFlpeJ2F19gDP6Y4ePZrGRvXsURvscePGUX3t2rVJLWqZfNppp1Gd1aMDwBe/+EWqs3bRP/vZz2js4sWLqR61uWa/e9Smmo1FBoD777+f6k888QTV2Sjst956i8ayWnjWSlpXdiEyQWYXIhNkdiEyQWYXIhNkdiEyQWYXIhNkdiEyoej17CxXHtWks1p41ksbiHP4S5cupfpZZ52V1J577jkau2fPHqoPHTqU6tFoYgarJwfiOv+obvvBBx+k+pQpU5JadM6jEd7nnnsu1dneiLKyMhq7detWqkd7H1iPAQD46KOPklo0spntCWF9F8Iru5nNMbNaM1t10m29zewlM3uv8Jnv3BBClJzGvIx/BMCVn7vtDgAL3P0MAAsK3wsh2jCh2d39VQCf75s0DcCjha8fBTC9hdclhGhhmvoGXX933174egeA5GZdM5tpZtVmVh3tXxdCtB7Nfjfe67vjJTvkuftsd69y96rOnTs393BCiCbSVLPvNLMKACh8rm25JQkhWoOmmv05ADcUvr4BwLMtsxwhRGsR5tnNbC6ASQD6mNlWAD8GcDeAP5rZzQA2A7i2UQdr3x79+vVL6ps3b6bx11xzTVJbuXIljWU5egC45ZZbqP7+++8ntZtuuonGvvLKK1SfOnUq1aP57yz+5ZdfprEdOnSgOqudBoC//e1vVGf7G8455xwaG+0BaM7+hREjRtDYaDZ8lKdfs2YN1dl5iXoQvP3220nt6NGjSS00u7tfn5AmR7FCiLaDtssKkQkyuxCZILMLkQkyuxCZILMLkQkWjYdtSQYOHOi33nprUi8vL6fxnTp1SmqsZTEADBkyhOpRiSxLQf3qV7+isWPHjqV6tI34wgsvpDorsb366qtp7AcffED1KDUXtXueMWNGUnvttddo7KWXXkr1bt26UZ216P7DH/5AY7/61a9SnbVsBuIx3fPmzUtqPXr0oLGsNflvfvMb1NTUNNg3XVd2ITJBZhciE2R2ITJBZhciE2R2ITJBZhciE2R2ITKhqHn2iooKv/HGG5P6pEmTaDzLy44ZM4bGshw9AAwaNIjqLC9aUVFBY08//XSqR/lm1sYa4O2Do/PCWnsDwBtvvEF11hIZANjjfeLECRob5fCjkmi292LYsGE0lo1UBoA+ffpQPdrX0bFjx6QWldeyc/6nP/0JtbW1yrMLkTMyuxCZILMLkQkyuxCZILMLkQkyuxCZILMLkQlFHdlsZrQ++vnnn6fxdXV1TY6dPJk3w43GBx85ciSpPfXUUzR2+nQ+Cm/9+vVUf+utt6i+d+/epPb1r3+dxkb17Gw8MBCPq2Zjk0eNGkVjoxbcrG0yAEybNi2p1dbyuSaffvop1VmtPAAcPnyY6mzfx4YNG2js4MGDkxqrs9eVXYhMkNmFyASZXYhMkNmFyASZXYhMkNmFyASZXYhMKGo9e2VlZbP6xrNxz7t27aKx8+fPp/q9995LdVZzHo2DjnLRjzzyCNUXLFhA9VNOOSWpRWONzz//fKqzUdUA0LVrV6qzfvxRv/yoZjx6vqxduzapjR8/nsYuXLiQ6tu2baP6xIkTqc4es2gGwpIlS5La4sWLsW/fvqbVs5vZHDOrNbNVJ912l5nVmNmywsdV0f0IIUpLY17GPwLgygZuv9/dxxQ+XmjZZQkhWprQ7O7+KoDdRViLEKIVac4bdN81sxWFl/m9Uj9kZjPNrNrMqqP9xkKI1qOpZv81gOEAxgDYDuC+1A+6+2x3r3L3qi5dujTxcEKI5tIks7v7Tnevc/cTAB4CMKFllyWEaGmaZHYzO7l38tUAVqV+VgjRNgjz7GY2F8AkAH0A7ATw48L3YwA4gE0AbnX37dHBBg4c6DNnzkzqu3fz9wG7d++e1FjesjGceuqpVGf54jfffJPGXnPNNVSfM2cO1a+99lqqs/7rUW/1qG981Hd+0aJFVGdz7aOa8GjGOXs+AMDx48eT2ooVK2js1KlTqc56CABx3/l33nknqUXnvFev5Ftk+MUvfoEtW7Y0mGcPm1e4+/UN3PxwFCeEaFtou6wQmSCzC5EJMrsQmSCzC5EJMrsQmVDUVtLl5eW0TJWNHgaAbt26JbWXX36ZxrL2uwBP0wA8zTNjxgwau3r1aqrfd19yAyKAuKUyS71FZaDR2OSoXXN0/2YNZoEAACNHjqSxbKwxwNN6kR6l7aJ06ttvv0111vYcAO68886ktnz5chq7cuXKpHbo0KGkpiu7EJkgswuRCTK7EJkgswuRCTK7EJkgswuRCTK7EJlQ1Dz7kSNHsHHjxqReVlZG49n436gcsqamhupR22JWshiVavbu3Zvq1113HdW/9rWvUf3pp59OaqykGIjHRb/44otUj1pVjx07NqlFbcpef/31Zh37tttuS2pRnjw6LxUVFVQfMmQI1dl5jfabnHnmmUmN7U3QlV2ITJDZhcgEmV2ITJDZhcgEmV2ITJDZhcgEmV2ITCh6PTurMY4mxrBRtl/4whdobHNaHgNAu3bpv4urVjWvbf4zzzxD9Q0bNlCdtRbu27cvjf35z39O9Wht7LwAwLvvvpvUJkzgs0Wi83rVVXx48OLFi5PaT37yExr705/+lOpR63FWVw7wfR3s8QT4vg7Wn0BXdiEyQWYXIhNkdiEyQWYXIhNkdiEyQWYXIhNkdiEyoah5dnfHsWPHknrUo5z1dl+yZAmNjfLoUb374cOHk1qUa45G8D700ENUj+qbmR71dY/yyVGdf9R3fsSIEUlt06ZNNHbgwIFUj+J79OiR1C644AIa+6Mf/YjqCxcupHo0p4DV07NzBgDjxo1Lamx0eXhlN7PBZrbQzNaY2Woz+17h9t5m9pKZvVf4zHcCCCFKSmNexh8H8AN3PxfARQC+Y2bnArgDwAJ3PwPAgsL3Qog2Smh2d9/u7ksLX+8HsBZAJYBpAB4t/NijAKa31iKFEM3nX3qDzsyGAhgLYDGA/u6+vSDtANDgP8VmNtPMqs2sOuo5JoRoPRptdjPrCuBpAN9393/o/OjuDsAbinP32e5e5e5VUaGLEKL1aJTZzawc9Ub/nbvPK9y808wqCnoFgNrWWaIQoiWw+osy+YH6mbuPAtjt7t8/6fb/APCxu99tZncA6O3u/8buq7Ky0r/1rW8ldTaSGQBN20UpoMsuu4zqv/3tb6l+4YUXJrUoBRSl/aL0VtTOubKyMqlF7ZZHjRpF9RUrVlD9yJEjVL/kkkuS2je/+U0ae/vtt1OdjS4GgCuuuCKpRam36upqqvfs2ZPq0XPik08+SWoff/wxjd2xY0dSq66uxr59+xqck92YPPtEADMArDSzZYXbZgG4G8AfzexmAJsBXNuI+xJClIjQ7O7+GoAG/1IAmNyyyxFCtBbaLitEJsjsQmSCzC5EJsjsQmSCzC5EJoR59pakoqLCb7rppqQe5Sb79euX1KJ8MstFA3F57cGDB5May3sCwNlnn0316DHo0KED1dnx67dJpIm2MEd7BLZu3Ur1Tp06JTWWawbi0mBWdgzwscrRY8b2dABxHn7atGlU37t3b1KLRnyz8tqFCxdiz549DT7ourILkQkyuxCZILMLkQkyuxCZILMLkQkyuxCZILMLkQlFH9k8YMCApM5a/wI893nOOefQ2CifzNpUA8C6deuS2g9/+EMa+8ADD1A9qq1evnw51dnvVlVVRWOjUdds7DEAbNu2jeosnx09ZqNHj6Y6GwcNAPv27UtqbM8GEOe67733Xqqz/gcA39exe/duGsv2XbB9FbqyC5EJMrsQmSCzC5EJMrsQmSCzC5EJMrsQmSCzC5EJRc2zHz9+HLt27UrqZWVlNL5Xr/Sg2EWLFtHYkSNHUj2qZ2e93efOnUtjWV01EOfRzzvvPKrv378/qUW18Pfccw/VJ0yYQPWoj8D48eOTWvR7R/XsLI8O8Fz59u3bkxoQzyGYOnVqk48N8BHjX/rSl2gsez68+eabSU1XdiEyQWYXIhNkdiEyQWYXIhNkdiEyQWYXIhNkdiEyoTHz2QcDeAxAfwAOYLa7/9LM7gJwC4DPEuez3P0Fdl9R3/hoVjirne7atSuNjfKerL85wOvZDxw4QGM3btxI9cGDB1O9pqaG6izvGuXoTzvtNKq/8sorVN+5cyfVJ06cmNTWr19PY6M55RGDBg1KalE/fTYnoDE669sA8Jr1VatW0VjGs88+i127djV5PvtxAD9w96Vm1g3A383spYJ2v7vzKn4hRJugMfPZtwPYXvh6v5mtBcDHqwgh2hz/0v/sZjYUwFgAn/Uq+q6ZrTCzOWbW4F5WM5tpZtVmVh299BFCtB6NNruZdQXwNIDvu/s+AL8GMBzAGNRf+e9rKM7dZ7t7lbtXde7cuQWWLIRoCo0yu5mVo97ov3P3eQDg7jvdvc7dTwB4CACvmBBClJTQ7Fb/tuXDANa6+3+edPvJpVxXA2j6W4hCiFanMe/GTwQwA8BKM1tWuG0WgOvNbAzq03GbANwa3VG7du1oiqw5LZOj1Fv0fsGWLVuo/uGHHya1aLxvlN6Kyimj9OiaNWuSWpRimjVrFtUvv/xyqkdpx3nz5iW1qOw4uu+1a9dSnZVMs8cTAKJ/OaPy2traWqqztfXt25fGduvWLamxkubGvBv/GoCGnjE0py6EaFtoB50QmSCzC5EJMrsQmSCzC5EJMrsQmSCzC5EJRW0lXVZWRvPh5eXlNJ61ko5y9FG+OTr25MmTk1rUxrp9e36ao3xz9+7dqc7GIm/evJnGTp8+nepRvrljx45UZwwfPpzqrO04UL9vg8HO++mnn96s+z58+DDVo7borF300qVLaSw7L2z0uK7sQmSCzC5EJsjsQmSCzC5EJsjsQmSCzC5EJsjsQmRC2Eq6RQ9mtgvAyYnfPgA+KtoC/jXa6tra6roAra2ptOTaTnP3Bgvii2r2fzq4WbW7V5VsAYS2ura2ui5Aa2sqxVqbXsYLkQkyuxCZUGqzzy7x8RltdW1tdV2A1tZUirK2kv7PLoQoHqW+sgshioTMLkQmlMTsZnalmb1rZhvM7I5SrCGFmW0ys5VmtszMqku8ljlmVmtmq066rbeZvWRm7xU+p4v8i7+2u8yspnDulpnZVSVa22AzW2hma8xstZl9r3B7Sc8dWVdRzlvR/2c3szIA6wFcDmArgCUArnf39KSDImJmmwBUuXvJN2CY2aUADgB4zN1HFm67B8Bud7+78Ieyl7v/extZ210ADpR6jHdhWlHFyWPGAUwHcCNKeO7Iuq5FEc5bKa7sEwBscPcP3P0ogN8DmFaCdbR53P1VALs/d/M0AI8Wvn4U9U+WopNYW5vA3be7+9LC1/sBfDZmvKTnjqyrKJTC7JUATp61tBVta967A5hvZn83s5mlXkwD9Hf37YWvdwDoX8rFNEA4xruYfG7MeJs5d00Zf95c9AbdP3Oxu18A4MsAvlN4udom8fr/wdpS7rRRY7yLRQNjxv+PUp67po4/by6lMHsNgMEnfT+ocFubwN1rCp9rAfwZbW8U9c7PJugWPvMJgkWkLY3xbmjMONrAuSvl+PNSmH0JgDPMbJiZdQBwHYDnSrCOf8LMuhTeOIGZdQEwBW1vFPVzAG4ofH0DgGdLuJZ/oK2M8U6NGUeJz13Jx5+7e9E/AFyF+nfk3wdwZynWkFjX6QCWFz5Wl3ptAOai/mXdMdS/t3EzgFMBLADwHoD/AdC7Da3tcQArAaxAvbEqSrS2i1H/En0FgGWFj6tKfe7Iuopy3rRdVohM0Bt0QmSCzC5EJsjsQmSCzC5EJsjsQmSCzC5EJsjsQmTC/wLS1XSqBh9vyQAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"generator = make_generator_model()\n",
"\n",
"noise = tf.random.normal([1, 100])\n",
"generated_image = generator(noise, training=False)\n",
"\n",
"plt.imshow(generated_image[0, :, :, 0], cmap='gray')"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "D0IKnaCtg6WE"
},
"source": [
"### 감별자 \n",
"감별자는 합성곱 신경망(Convolutional Neural Network, CNN) 기반의 이미지 분류기입니다. "
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"execution": {
"iopub.execute_input": "2020-09-23T04:26:36.318210Z",
"iopub.status.busy": "2020-09-23T04:26:36.317560Z",
"iopub.status.idle": "2020-09-23T04:26:36.319996Z",
"shell.execute_reply": "2020-09-23T04:26:36.319416Z"
},
"id": "dw2tPLmk2pEP"
},
"outputs": [],
"source": [
"def make_discriminator_model():\n",
" model = tf.keras.Sequential()\n",
" model.add(layers.Conv2D(64, (5, 5), strides=(2, 2), padding='same',\n",
" input_shape=[28, 28, 1]))\n",
" model.add(layers.LeakyReLU())\n",
" model.add(layers.Dropout(0.3))\n",
"\n",
" model.add(layers.Conv2D(128, (5, 5), strides=(2, 2), padding='same'))\n",
" model.add(layers.LeakyReLU())\n",
" model.add(layers.Dropout(0.3))\n",
"\n",
" model.add(layers.Flatten())\n",
" model.add(layers.Dense(1))\n",
"\n",
" return model"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "QhPneagzCaQv"
},
"source": [
"(아직까지 훈련이 되지 않은) 감별자를 사용하여, 생성된 이미지가 진짜인지 가짜인지 판별합니다. 모델은 진짜 이미지에는 양수의 값 (positive values)을, 가짜 이미지에는 음수의 값 (negative values)을 출력하도록 훈련되어집니다."
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"execution": {
"iopub.execute_input": "2020-09-23T04:26:36.326242Z",
"iopub.status.busy": "2020-09-23T04:26:36.325611Z",
"iopub.status.idle": "2020-09-23T04:26:36.412737Z",
"shell.execute_reply": "2020-09-23T04:26:36.412180Z"
},
"id": "gDkA05NE6QMs"
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"tf.Tensor([[0.00130089]], shape=(1, 1), dtype=float32)\n"
]
}
],
"source": [
"discriminator = make_discriminator_model()\n",
"decision = discriminator(generated_image)\n",
"print (decision)"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "0FMYgY_mPfTi"
},
"source": [
"## 손실함수와 옵티마이저 정의\n",
"두 모델의 손실함수와 옵티마이저를 정의합니다. "
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"execution": {
"iopub.execute_input": "2020-09-23T04:26:36.417149Z",
"iopub.status.busy": "2020-09-23T04:26:36.416480Z",
"iopub.status.idle": "2020-09-23T04:26:36.418385Z",
"shell.execute_reply": "2020-09-23T04:26:36.418806Z"
},
"id": "psQfmXxYKU3X"
},
"outputs": [],
"source": [
"# 이 메서드는 크로스 엔트로피 손실함수 (cross entropy loss)를 계산하기 위해 헬퍼 (helper) 함수를 반환합니다.\n",
"cross_entropy = tf.keras.losses.BinaryCrossentropy(from_logits=True)"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "PKY_iPSPNWoj"
},
"source": [
"### 감별자 손실함수\n",
"\n",
"이 메서드는 감별자가 가짜 이미지에서 얼마나 진짜 이미지를 잘 판별하는지 수치화합니다. 진짜 이미지에 대한 감별자의 예측과 1로 이루어진 행렬을 비교하고, 가짜 (생성된) 이미지에 대한 감별자의 예측과 0으로 이루어진 행렬을 비교합니다."
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"execution": {
"iopub.execute_input": "2020-09-23T04:26:36.423584Z",
"iopub.status.busy": "2020-09-23T04:26:36.422954Z",
"iopub.status.idle": "2020-09-23T04:26:36.424865Z",
"shell.execute_reply": "2020-09-23T04:26:36.425270Z"
},
"id": "wkMNfBWlT-PV"
},
"outputs": [],
"source": [
"def discriminator_loss(real_output, fake_output):\n",
" real_loss = cross_entropy(tf.ones_like(real_output), real_output)\n",
" fake_loss = cross_entropy(tf.zeros_like(fake_output), fake_output)\n",
" total_loss = real_loss + fake_loss\n",
" return total_loss"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "Jd-3GCUEiKtv"
},
"source": [
"### 생성자 손실함수\n",
"\n",
"생성자의 손실함수는 감별자를 얼마나 잘 속였는지에 대해 수치화를 합니다. 직관적으로 생성자가 원활히 수행되고 있다면, 감별자는 가짜 이미지를 진짜 (또는 1)로 분류를 할 것입니다. 여기서 우리는 생성된 이미지에 대한 감별자의 결정을 1로 이루어진 행렬과 비교를 할 것입니다. "
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"execution": {
"iopub.execute_input": "2020-09-23T04:26:36.429526Z",
"iopub.status.busy": "2020-09-23T04:26:36.428917Z",
"iopub.status.idle": "2020-09-23T04:26:36.430846Z",
"shell.execute_reply": "2020-09-23T04:26:36.431263Z"
},
"id": "90BIcCKcDMxz"
},
"outputs": [],
"source": [
"def generator_loss(fake_output):\n",
" return cross_entropy(tf.ones_like(fake_output), fake_output)"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "MgIc7i0th_Iu"
},
"source": [
"감별자와 생성자는 따로 훈련되기 때문에, 감별자와 생성자의 옵티마이저는 다릅니다."
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"execution": {
"iopub.execute_input": "2020-09-23T04:26:36.435553Z",
"iopub.status.busy": "2020-09-23T04:26:36.434933Z",
"iopub.status.idle": "2020-09-23T04:26:36.437254Z",
"shell.execute_reply": "2020-09-23T04:26:36.436747Z"
},
"id": "iWCn_PVdEJZ7"
},
"outputs": [],
"source": [
"generator_optimizer = tf.keras.optimizers.Adam(1e-4)\n",
"discriminator_optimizer = tf.keras.optimizers.Adam(1e-4)"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "mWtinsGDPJlV"
},
"source": [
"### 체크포인트 저장\n",
"이 노트북은 오랫동안 진행되는 훈련이 방해되는 경우에 유용하게 쓰일 수 있는 모델의 저장방법과 복구방법을 보여줍니다. "
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {
"execution": {
"iopub.execute_input": "2020-09-23T04:26:36.442138Z",
"iopub.status.busy": "2020-09-23T04:26:36.441471Z",
"iopub.status.idle": "2020-09-23T04:26:36.443923Z",
"shell.execute_reply": "2020-09-23T04:26:36.443292Z"
},
"id": "CA1w-7s2POEy"
},
"outputs": [],
"source": [
"checkpoint_dir = './training_checkpoints'\n",
"checkpoint_prefix = os.path.join(checkpoint_dir, \"ckpt\")\n",
"checkpoint = tf.train.Checkpoint(generator_optimizer=generator_optimizer,\n",
" discriminator_optimizer=discriminator_optimizer,\n",
" generator=generator,\n",
" discriminator=discriminator)"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "Rw1fkAczTQYh"
},
"source": [
"## 훈련 루프 정의하기"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"execution": {
"iopub.execute_input": "2020-09-23T04:26:36.448587Z",
"iopub.status.busy": "2020-09-23T04:26:36.447879Z",
"iopub.status.idle": "2020-09-23T04:26:36.450031Z",
"shell.execute_reply": "2020-09-23T04:26:36.450461Z"
},
"id": "NS2GWywBbAWo"
},
"outputs": [],
"source": [
"EPOCHS = 50\n",
"noise_dim = 100\n",
"num_examples_to_generate = 16\n",
"\n",
"# 이 시드를 시간이 지나도 재활용하겠습니다. \n",
"# (GIF 애니메이션에서 진전 내용을 시각화하는데 쉽기 때문입니다.) \n",
"seed = tf.random.normal([num_examples_to_generate, noise_dim])"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "jylSonrqSWfi"
},
"source": [
"훈련 루프는 생성자가 입력으로 랜덤시드를 받는 것으로부터 시작됩니다. 그 시드값을 사용하여 이미지를 생성합니다. 감별자를 사용하여 (훈련 세트에서 갖고온) 진짜 이미지와 (생성자가 생성해낸) 가짜이미지를 분류합니다. 각 모델의 손실을 계산하고, 그래디언트 (gradients)를 사용해 생성자와 감별자를 업데이트합니다."
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {
"execution": {
"iopub.execute_input": "2020-09-23T04:26:36.457358Z",
"iopub.status.busy": "2020-09-23T04:26:36.456712Z",
"iopub.status.idle": "2020-09-23T04:26:36.458607Z",
"shell.execute_reply": "2020-09-23T04:26:36.459040Z"
},
"id": "3t5ibNo05jCB"
},
"outputs": [],
"source": [
"# `tf.function`이 어떻게 사용되는지 주목해 주세요.\n",
"# 이 데코레이터는 함수를 \"컴파일\"합니다.\n",
"@tf.function\n",
"def train_step(images):\n",
" noise = tf.random.normal([BATCH_SIZE, noise_dim])\n",
"\n",
" with tf.GradientTape() as gen_tape, tf.GradientTape() as disc_tape:\n",
" generated_images = generator(noise, training=True)\n",
"\n",
" real_output = discriminator(images, training=True)\n",
" fake_output = discriminator(generated_images, training=True)\n",
"\n",
" gen_loss = generator_loss(fake_output)\n",
" disc_loss = discriminator_loss(real_output, fake_output)\n",
"\n",
" gradients_of_generator = gen_tape.gradient(gen_loss, generator.trainable_variables)\n",
" gradients_of_discriminator = disc_tape.gradient(disc_loss, discriminator.trainable_variables)\n",
"\n",
" generator_optimizer.apply_gradients(zip(gradients_of_generator, generator.trainable_variables))\n",
" discriminator_optimizer.apply_gradients(zip(gradients_of_discriminator, discriminator.trainable_variables))"
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {
"execution": {
"iopub.execute_input": "2020-09-23T04:26:36.465062Z",
"iopub.status.busy": "2020-09-23T04:26:36.464426Z",
"iopub.status.idle": "2020-09-23T04:26:36.466310Z",
"shell.execute_reply": "2020-09-23T04:26:36.466708Z"
},
"id": "2M7LmLtGEMQJ"
},
"outputs": [],
"source": [
"def train(dataset, epochs):\n",
" for epoch in range(epochs):\n",
" start = time.time()\n",
"\n",
" for image_batch in dataset:\n",
" train_step(image_batch)\n",
"\n",
" # GIF를 위한 이미지를 바로 생성합니다.\n",
" display.clear_output(wait=True)\n",
" generate_and_save_images(generator,\n",
" epoch + 1,\n",
" seed)\n",
"\n",
" # 15 에포크가 지날 때마다 모델을 저장합니다.\n",
" if (epoch + 1) % 15 == 0:\n",
" checkpoint.save(file_prefix = checkpoint_prefix)\n",
" \n",
" # print (' 에포크 {} 에서 걸린 시간은 {} 초 입니다'.format(epoch +1, time.time()-start))\n",
" print ('Time for epoch {} is {} sec'.format(epoch + 1, time.time()-start))\n",
"\n",
" # 마지막 에포크가 끝난 후 생성합니다.\n",
" display.clear_output(wait=True)\n",
" generate_and_save_images(generator,\n",
" epochs,\n",
" seed)"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "2aFF7Hk3XdeW"
},
"source": [
"**이미지 생성 및 저장**\n"
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {
"execution": {
"iopub.execute_input": "2020-09-23T04:26:36.473053Z",
"iopub.status.busy": "2020-09-23T04:26:36.472379Z",
"iopub.status.idle": "2020-09-23T04:26:36.474229Z",
"shell.execute_reply": "2020-09-23T04:26:36.474636Z"
},
"id": "RmdVsmvhPxyy"
},
"outputs": [],
"source": [
"def generate_and_save_images(model, epoch, test_input):\n",
" # `training`이 False로 맞춰진 것을 주목하세요.\n",
" # 이렇게 하면 (배치정규화를 포함하여) 모든 층들이 추론 모드로 실행됩니다. \n",
" predictions = model(test_input, training=False)\n",
"\n",
" fig = plt.figure(figsize=(4,4))\n",
"\n",
" for i in range(predictions.shape[0]):\n",
" plt.subplot(4, 4, i+1)\n",
" plt.imshow(predictions[i, :, :, 0] * 127.5 + 127.5, cmap='gray')\n",
" plt.axis('off')\n",
"\n",
" plt.savefig('image_at_epoch_{:04d}.png'.format(epoch))\n",
" plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "dZrd4CdjR-Fp"
},
"source": [
"## 모델 훈련\n",
"위에 정의된 `train()` 메서드를 생성자와 감별자를 동시에 훈련하기 위해 호출합니다. 생성적 적대 신경망을 학습하는 것은 매우 까다로울 수 있습니다. 생성자와 감별자가 서로를 제압하지 않는 것이 중요합니다. (예를 들어 학습률이 비슷하면 한쪽이 우세해집니다.)\n",
"훈련 초반부에는 생성된 이미지는 랜덤한 노이즈처럼 보입니다. 훈련이 진행될수록, 생성된 숫자는 점차 진짜처럼 보일 것입니다. 약 50 에포크가 지난 후, MNIST 숫자와 닮은 이미지가 생성됩니다. 코랩에서 기본 설정으로 실행하면, 에포크마다 1분정도 소요될 것입니다."
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {
"execution": {
"iopub.execute_input": "2020-09-23T04:26:36.479786Z",
"iopub.status.busy": "2020-09-23T04:26:36.479148Z",
"iopub.status.idle": "2020-09-23T06:52:40.800934Z",
"shell.execute_reply": "2020-09-23T06:52:40.801458Z"
},
"id": "Ly3UN0SLLY2l"
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAOwAAADnCAYAAAAdFLrXAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAgAElEQVR4nOx9aXCb13X2gxf7vgMkuIH7vomiZNGKJWux7NqOPaodN3ESO6njeqaN22mmk5lkOtNJ4k6aL23adCaJnMSVR66TTBYnkRcptmPZkqyVKyhSXESCC0iQALHv2/v9UO81qJWSAAK08cxgbIHgy3tx77n3LM85h8OyLAoooICNASbXAyiggALWjoLAFlDABkJBYAsoYAOhILAFFLCBUBDYAgrYQODd6IcMw7AAkCtPMofDWfXvWx0Hy7Kcm38K4HK5LMuya3o+h8MBl8sFh8MBwzD0/+PxOJLJJFKp1Lp/X2udJwBwOJwNHRZY61zzbZ5kv/B4PAiFQvB4PESjUaRSKbpvkskk3U+xWOya87yhwAK5FVYyyWwLwVqfTQ4QLpcLHo8HsVgMPp8PLpcLv9+PeDxOF6EQLisgHRwOB3w+H3K5HFqtFjKZDB6PB9FoFB6PB7FYDKlU6qbPuaHA5nLTkZuMx+MhHo9nVQhu5bkcDgcCgQAymQxGoxFSqRQCgQBzc3MIBAJYWVkBACSTyayMtYCNCYZhIJVKUVFRgZaWFlRUVGBqagpOpxNDQ0MIBAJIJBL0oroebnrDrjeIoIpEIvrvRCKR41FdBsuy9MuUy+VobGyEwWCAQqGA3++H0+nE+++/D5/PB5/PV7hlCwBwWViVSiXq6+vxyCOPoKKiAkajEW1tbXA6nVCpVLDZbJienqbq8fWQNwJL1F+i54tEIqrX3+jEyRVEIhFKSkpQWloKrVYLALDb7RgaGkI8Hoff7y8IbAEAPhLYiooK7Ny5E3q9HiqVCvF4HE6nE8FgEHK5HNFoFJFI5IYXVM4FlghnUVERtFot+Hw+UqkUXC4XfD4fVlZWkEgk1qTfrwdSqRSCwSAmJyexvLwMqVQKkUgEmUwG4LIqTJxRa3VkFfDxhUwmg1KpxJ49e1BfXw+BQED3Bo/Hg1arxf3334+77roLTqcTKysrCIfD133eugqsQCCAUCiEWq2GWCyGWCyGQCCAWCxGcXEx1Go1AMDv98PlciGZTCKZTObdpk+lUgiFQgiHw+Dz+eDxeJDJZODz+RCJRGBZFgKBACzL5o06X0D2QRxLSqUSfD4fAoEAOp0OGo0GpaWlUCgU8Pl8SCQS8Hq9EAqFVHvk8/mQyWQIBAI39H9wbiQMmXaNl5aWora2Fo8++igaGxvR0dFBXdwMczkkvLS0hP7+fjz11FMIhUJ3tOHXMwRAnAVcLhcSiQRyuRxutxuRSCTrDqhCWOdqrPc8ORwOhEIhdDod7r//fphMJpSWlqK5uRlyuRxjY2PweDyw2+3w+XwIhUKoqKiASCRCMplEIBCA1+ulzsvXX3/99sI6mQCfz4dWq8WmTZuwd+9edHR0oLi4GAqFggorh8MBy7JUcBOJxIbytBL1N/2UbW1tBZ/Px3vvvYdwOFy4bT9mEIlE0Gg0aG9vR21tLQQCAXVGKpVKqFQqaDQacDgcRCIRLC8v4/z58wgEAohEIpiZmQGPxwPLsohGowiHwzTUcz2si8AKhUJUVFRgx44d+MpXvgI+n08F80rE43HEYrG8VIXXglQqRdX+Rx55BAaDAUNDQ1heXt6wc8oErgxXbET7noyfXC4ymQxVVVV4+umnsX//fkp6AD6an9frhdfrRSgUwtzcHI4dO4ZoNEpDleSza8W6CKxMJkNPTw9qampuKKyxWAz/9V//hb6+PsTj8fUYWkbB4/GgVCpxzz334LOf/Szq6uoglUrx4osvIhKJIBKJ4MyZM7BYLDh9+jR8Pl+uh5xVMAwDPp+Pe+65B2azGffccw91uBw/fhxTU1N4//33b3ij5BOIBsXhcCASidDe3o5vfvObqK2tXSWsV/5OIpGAx+NBOByGVCpFMplELBa7rQNr3VTi4uJiKJXKG96sgUAA58+fx+DgYN54hW8GEo5SKpUQi8UwGo1obGxEd3c3FAoFBAIBSkpKkEqlEIvFqAkwOzsLhmHg8XhyPYWMgwiqQqGAQqFAe3s7Ghsb8eCDD1LmWiKRgFgsxqlTpzaMwBJwOBxIJBKYTCb09PSAx+NdJaxEKL1eL1wuFxVYIti3q12si8AmEgm43W6EQiGkUqmrhJZlWYyMjGB0dBR2ux2hUGg9hpURyOVyqFQqfOMb30B9fT0qKyshk8kgl8vp4qSTQR544AHs3LkT9913HwYGBvDNb34TsVgs19PIKNRqNRobG/GFL3wBe/fuhUqlAp/Ph0QioRt7//792Lp1K1577TVEo9EN8x2QcExHRwfq6upWOUwJUqkUbDYbxsfHcfToUUxNTWFxcRF+v5/GWfNaYPl8PoxGI+Ry+VUnUTgcxsrKCiwWC86ePZv3hAMOhwMejweFQoGKigqYTCYUFxejubkZ5eXlMBqN1IkWCoWQTCYhkUjA5XKp0AqFQlRVVcHtdt/xiZsvYBgGAoEAdXV1KCkpQVdXF5qammAyma5pBslkMuqwEYlEuHjxYo5Gfmsg3uDm5maYzeZVtjnLsohEIpibm8PIyAh6e3thsViwsLCAQCCAWCyGaDR6R87UdbNhu7u7UV5efpXjwe124+zZs3j11Vdx5MiRvN246ckIUqkUzc3NeOqpp7B582bU1dVBIBDQTUkYWkRbKCkpWUWu4HA4VGAFAgF1sm1k8Hg8qNVqPPPMM2hqakJPTw+NUV8PMpkMTz/9ND744IMNI7BcLhdyuRyPPvooqqqqVu3nZDKJlZUV/PGPf8Tx48dx5MiRjJN+si6wRBUiYRwC4sqemJjASy+9hNHR0bwTVnKakvgxuSXFYjFKS0uhVqshEAioTQZcdpxNTk5icHAQfX19cDgckMvlaG1txZe//GUIBAK6ibVaLf7qr/4KAwMDOHPmTC6netuoqalBa2sr2traYDKZsGXLFspY43A4SCaTCIfDSCaTiEajEIvFkMvlAC7vjZaWFszPz1PbNt9RWlqKyspK6HQ6SKVSsCxLD+i+vj6MjY3h8OHDmJ2dzQpDL+sCKxAIIBKJoNVqIZVK6ftEYOfm5vDWW2/l3WKlp0NVVlZi27Zt4HK5lHYol8vB5/Ops4x4P8PhMEZHR3H06FGcOHECCwsLAIAHHngATzzxBOVKA4BSqcR9992HWCyGgYGBVa7+fAc5zCorK7Fr1y7s27cPFRUVdG5EWJPJJHw+H6LRKILBIE0tI6aF2WxGSUkJhEJh3msaHA4HRUVFqKqqok5GlmWRTCYRiUQwPDyMvr4+nDp1KmtRjqwKLMMwqK2tRX19/VV2TDKZxMzMDJaWlvLuZmUYBkVFRaisrMRzzz0HlUoFuVyO6elpLC4u4ne/+x1Nh+LxeODxeOByuQAuH0Q+nw9utxt+v59uwPn5ebz22mvo6elBS0sLAEChUGDXrl0oLS3FXXfdhQMHDmBoaOiWCBa5SowoLS3FV7/6VbS0tKCrq4uSYIigJhIJOJ1OOBwOHDhwAC6XC6Wlpdi+fTsefPBBuh8YhkF5eTk+97nP4dSpUxgZGcnJfG4Gwnnfv38/PvWpT0GtVoPH4yGRSGB2dhZzc3M4ePAgxsfHs0qQybrAlpWVobS09Ko4VSqVgs/nQzAYzLnApjsNyA1aXl6OhoYGtLa2UsK/2+3GwsICbDbbqrGnx+fIc67M3/X5fBgaGkJdXR31lHO5XKhUKpjNZjAMg66uLjAMA5vNhnA4jEAgsOrGJc6pa/3N9QRh+LS1taG6uhp6vR6pVArxeBw2mw2hUIimGzocDlgsFsqhbWxsRDKZXGXbKpVKtLW1YWpqClNTU4hGoznfE1dCrVajpKQE1dXVqKiogFAoBHA5ArKwsIALFy5gdnYWDocjq+PIqsDyeDzcd9992LRpE72BCJLJJJaWluB2u7M5hFsCUdMkEgm+/OUvo7W1FRUVFZiYmMDw8DBeffVVDA8P39aGmp2dxaFDh1BXV4fNmzdDIpFQjUOv10On0+GHP/whXC4X/vM//xOjo6M4deoUYrEYvckBUDUzHo9Tb/R6gmEYmM1mNDU1obu7m5o54XAYDocD3/72tzE5OYmLFy9SGy4Wi0EikUCpVMLr9a6KR3M4HJSWluKJJ56A3W6HzWbDzMxM3sVmt23bhmeeeQZdXV0wGAw0TzsajeLo0aP4xS9+gaWlpayPI2sCy+VyIRQKYTAYoNPprvIOA5cpi2KxGFKpFNFoNC+4tmRsJLOIx+PB5XJhaGgILpfrthkqxPkyMDCAN998E7t374ZaraabltiEKpUK99xzD2pqalBbW4vZ2VksLi5iZmYGwWBwFW0zlUqtq8Cq1WoolUrs3bsXTU1N4HA4cDgcWFlZQW9vL6xWKywWCxwOB03gJ69IJIKlpSXMzc1hYmIC1dXVUKlUAC4fAmKxGEVFRTCbzbDb7XklsDweDxqNBrW1tZDL5fSgTc/GuhZ5IitjydaD+Xw+XQRyIhGkUimkUilIJBKaL+j1eq9yOKyXWpT+d9IFgaitS0tLOHv2LFZWVm7bKcSyLOLxOE6ePAm73Y6WlhbquErnqEokEjz44IOIxWLw+/04duwYent78frrr9NDjajb6602GgwGVFVV4TOf+QzMZjO13wYGBvDTn/4UFovluk6jSCRCyQT9/f3Q6XRQKpUALgusUChEcXEx6urqMDAwkDe0TRJf1uv1aGhooO+T7z+RSEAkEkGpVFIHYzaRNYHdvHkzNm3ahOLiYlruhbi/FxYW4HK5MDc3h7KyMhw4cGDVaRwOhzE1NYXz58/j2LFjCAQC68YtJuGH3t5exONxFBcXw+fzwePxZGQMNpsNHo8Hzz//PNRqNXQ6He6++248/PDDkEgk9KQmHurOzk4YDAacOnUKTqczZ6R5hmGwY8cOPPTQQygvL0cgEMDBgwdx8eJFDA4OYnZ29oYe3lQqhWg0ivHxcfz+97+nnlaZTIZEIgG/34+xsTGcP38ewWBwHWd2YxQVFeGZZ57B3Xffvep9skZqtRr3338/Kioq8C//8i+wWq1ZHU9WBJY4mzo6Oqj3kKhFoVAIs7OzWF5extLSEi2bQdRPlmURDAYxPDyMVCqF6elpGhYgm5XwNElmDzkIMgHy/Lm5OWg0Gvp3SDXEO0UwGEQwGMSxY8cgFApRVFREieQlJSX01iUnu9FopKYDwzA5E1Yej0fXlOT69vb24uLFi2smPaRSKXg8HszOzsLn89EwFtEmnE4nFhYW8ibxg2EYKBQK9PT0oKqq6qqfkzBfVVUVJBIJdDodlpaWblgx4k6RcYElN0N3dzc+/elPU8J/LBaDxWLBBx98gHfeeQfz8/NQKBTo7u7Gpk2baJ0bDocDmUyGrq4utLS04Nlnn6UqdCwWQygUgsPhwPnz53HhwgX09/fD6XTCZrNlbDOnUimMjIyAx+NRJ89ay1CuFcSmnZ2dxUsvvYTf/va3+Na3voVPfepTNJ5JVGQA9EDLBYRCIfR6PfR6PdRqNbhcLo0du1yuW3qWXC5HWVkZNBoNpFIprWvU29uLyclJ2O32vBFYpVKJkpISbNmyhbLUrgSHw4FGo4FEIsHDDz+M0tJSHD58OGvx5IzvALFYDJPJRIkShFM7NjaGgYEB9Pb2YmpqCi6Xi75/9OhRqFQqyGQycLlcKBQKdHZ2QigUUlYMcDmjJxKJQKFQIBaLQSqVYmJi4pY3zc3AsixCoRCteCGVSlFeXo5YLJYxkjqxWxOJBE1odjgccLlcKCsrW/U58p0oFIqc8I6lUimqq6uh0WjA5/MBXA7tVFdXg2GYNdmb6XZqe3s7lEolzRddWFhAf38/lpaW7ogYn0lwuVy0tbWhra2Nlv0h2mEoFILJZIJEIoFCoaDaUFtbG8RiMUKhEKampjA5OZnxcWVcYNVqNbq7u1FcXEwX1+Fw4NChQzh//jxOnjxJP+tyuWC1WvGnP/2JbmCJRIKWlha8+OKL1GFFwOfz6Q1uMpmwbds2vP7661nxLofDYeqVNZlM2L17Nzwezx2nwxGP8JWCl0qlsLi4CKvViubmZggEAvp5Qi5wOp0YHR29o79/OzAYDNizZw/MZjMtkqfT6fD444/jnXfegdVqvan2QQqObd26FU8//TR0Oh0SiQRsNht6e3tx6NAheL3evGB6kdrTTz31FDo6OsDlchEKheDxePCrX/0KMzMz2L9/PyoqKtDa2grg8vweffRRhMNhPPTQQ3j55Zfxb//2bxkfW8YFtqioCJ/+9Kepzr+4uIjJyclVNL1rgWzeaDQKq9WK7373u5BKpZBKpXjmmWcoO4ggHo8jHA7D7XbD6/Vm9FQm9nY8HodMJkNtbS1EIhFOnDgBq9V6RweERqOBXC6nt3c0GoVAIIBEIkFtbS0aGhquUn1JrHJ5eRlcLndd6XscDgdqtZrGH8l7UqmU2rO1tbV4++23MTMzQ9ldJEtJIpFQ5+OmTZtQW1sLmUxGBeDgwYMYGxuj8dl8ACntcunSJTidThw6dIj6X0ZHR+Hz+eBwOKDX61FVVYV9+/ahu7sbwOVwYFFREXQ6HV3nTK5XxgVWo9Ggp6cHMpkMLMtieXkZMzMzlHBwMyQSCSwtLeEXv/gFVQf37NlzlcBGIhF4vV7KOMo0CGGBqD06nQ4GgwESieQqBtK1kH6Tks+SRHeDwUC9zqFQCFKplNatLS8vXyWwZPOr1Wqo1epr3s7ZBlGJSRgmlUqBz+fDbDZDr9ejqakJi4uLCIfDNNSRPuaenh7U19djz549AD5a49nZWRw5cgRLS0uIRCJ5oQoDoO00ZmdnEQ6HceTIkavqBV+8eBEymQwlJSUoLi5GY2MjdQyq1WqoVCooFAracylTyKjAEle3RCIBn89HIpHAiy++SEMktwoSE00kEqvYPgBw6NAh/O53v8PMzEwmp0BBqJTRaJQSGp555hls3boVP/jBD+B2u695I5BsHplMBrPZDLFYTB1Yer0excXF0Ol0tHwMqbRHYpBisZgKeTKZxMTEBKampnDo0CFcunQpJ+R4n8+H0dFR1NXVgWEYDA8Pw+VyweFw0PV+8MEHsW/fPtjtdtqSQqFQQCqVQqvV0vTCCxcu4PTp0zh8+DAmJiawsLCQN3Yr8YYTDevdd99FOBymhReuRCgUgtVqxXe+8x387Gc/w3e+8x3U1dVBr9ejpqYGTz75JH73u99l1JbNqMDyeDxqZzIMg2g0ipmZGczNzd32glzv9wh/M1sudEKaIAvF4/FQXV0NHo+HTZs2UYElP0+/RaVSKU1wFwqFdCMYjUZ68lZVVVFHkkajoQn+JOsnFApRm3VkZATT09Ow2+05sfFisRjsdjvkcjlYlsXw8DDlCYtEIkilUhiNRojFYqhUKhiNRrS3t0Mqla4KR4VCIdodYXR0NOsxy7WCUFLJ4cPlchGNRuFyuRCJRK77eyS2bLVasbi4iL6+PiSTSbr+jY2NKCoqgsPhgN/vz8jaZUxgGYahWS0kRzSZTMLpdNKA/+2CNMVKRyAQgMPhyNrJTDJw0sut1tTUoLq6Gtu3b6cZKeRFypgSNVomk1F11uPxUOohsY3Jv00mEwQCwSrGUyKRgNVqxW9+8xu8/fbbVEPJlUPG5XKhr68Pk5OTEAgE+PWvfw273U4PSw6HA7lcTivcb968Gbt3715VPiUSiWB+fh7Hjx/Hz3/+87ygoQIfeeH1ej0UCgVKSkpgs9lox4m1IhqN4lvf+hZaWlpw4MABqNVq7Nu3DzMzM1AqlbTU7Z3u14wKLImlElwra+VWQGxHEosEPmIixePxrKpRsVgMy8vLeP3119He3o7NmzfT5HNyC6b39pRIJJSUT6q+k7mTmCqPx6NEjFQqRU/19EymcDiMd999FxcvXsSHH36Iubm5nPJqWZaF3++HxWKBSCQCj8ej7STIGnA4HAQCAbAsC5vNhsrKylXPIDf0//7v/+Ls2bN5EWcl3veysjLodDp0d3dT7WBiYgKzs7M4fvz4LUUFSKqlUCikDrdt27ahuLgY5eXlsNvtGB0dpamXt9OaNGMCy+Vyafw1U/Q5nU6HlpaWVZUqCI0t24sejUZhs9nw8ssvY//+/WhqaqIVJ9LLxZCbXywWUxWJCDO5YUg8muSKklQ0YDVpnCR7v/LKKxgbG8Pg4GBW57hWuFwunD17liYqXEkiITZfKpXC7OwszXFOp5pOT0/jBz/4Qd4U2CNr19zcjMbGRjz55JNQq9VQKBQYHBzE6OgoTQtci2ZDWFFqtZpGN6RSKfbs2YNEIoHl5WWa8TU6Ooq5uTl6wOdEYBOJBCYnJ1FbWwvgI1WD5Hj29/fT0yQ9b/RakEqlaG1txb333otHH32UPhMAhoaG8P3vfx99fX2ZGvo1kUqlEA6HMTk5iVdffRXnzp3D008/jdbWVpSWll4zO4Pcoun/JoJNkC70wEebPRaL4f3338fo6CjOnj2bcTLInYB4ftM91FdmX5EWJTt37kRnZycV7ng8jgMHDqCvry+v8lx1Oh0qKirwyCOPoKOjA+Xl5TRDi/RvNZlMmJycxMGDB2kLUZJ8QcwkhmHQ2tqK2tpa7Nq1CxUVFdBoNBAIBPQ7Itk+TU1NNFHfYrFgcHCQxvbXau5kTGBTqRTcbjd8Ph9tEcnlclFdXU1ZPCQtLH3hr7WASqUSzc3N6OjowJYtWwBc3hSBQAAzMzP485//jEAgkKmhXxekAHQwGITVakVnZyfEYjEAUMcaKTSWTtonlRQArArrpGflMAxDWU6BQAAejwcDAwOwWCxZ56PeDtKT5oHVYStijysUCtTU1KCkpGSVPd7f34/+/v68Kv9CkvArKytpbJism1arhUajgVarRXl5Oc6cOQOn0wmXy0V9GsS+ZRgGTU1NaG9vx/bt22EwGFY1uboydbKmpgYLCwtwu92Ynp6mtYvXGqrLmMASgXK5XLDb7VAqlZBIJHj22WepM2atIBMkWT7AZSfTSy+9hHPnzsHlcq2rAyYejyORSOD73/8+tWOJrVJXV0cTugk5QCqVUrub3KCEvkYI4yQW+etf/xpDQ0N0XuFw+IaeyVyCbELiBJTL5RCJRJBIJKiqqkJpaSm2bt2K4uJimuAdiUQwNTUFq9WaN7crcNnkIcW9iXlypZDJ5XK0tLTgJz/5CeWzkzmk/5c4DYmgxmKxVZoUqV/m8/kwPz+PRCIBmUyG4uJiAIDT6VxzvDajYR1yy/b29qKurg6lpaWUH3wn5UxIobPBwUFMTk7mxFtKajURkNuVw+HA7/cjGAxCo9HA4XBQ+4UsMhFYiUQCvV4PpVKJZDKJxcVFDA0N0XjkndaszTbIDZvOCzYYDCgtLUVZWRkMBgO0Wi0kEgm1Xb1eL/WM5xMikQjcbjdmZmZgMBjQ1NREnWrpgsvn86HRaK77nPRDiNy8xMRJzyQjHQCmpqZgt9vh9/tXOe7WiowKLMuymJqawo9//GM8/vjj2LlzJ8rKyiin+HYRCARgt9vx5ptvrksZjrWAOJgmJycp9ZLYsMRLSKpDxGIxCAQCmqrV3NwMlmVht9tx5MgRhEKhvKqwcDMwDENzdTdv3owdO3ZAJpNBJBLRKhqkKffc3FxesZgISMvHP//5z3A4HDAYDJQ2SrCWCyb9M4Rq6na7sbS0hPn5eaoxWa1W+Hw+LCwsUGfT4uIiNSHTv58b/d2MUxP9fj9GR0fx6quv4oMPPoBCoUBRUREee+wxaLXaq8rFEJCTaHFxES6XC8PDw1haWqJFvQgNMZ+RXjIkvRk18QynUin09/djbm4OAFZlBG0UkMoZgUAAly5dgtFohNPphEgkAofDoRQ+v9+Po0eP0sT7fANZq8HBQVpHSiQSUa2J+GBUKhUNzZjNZkqEIQKWSqWwsrKClZUVnDlzBg6HA/Pz8/D7/bR1JGngHIvFaOG+VCpF37uV0E7GBTYcDmNubo5uSlLqtK2tDZWVlZT5ciUSiQRisRhmZmYwMzODN998kxY/y3QuajZBNvSVKiAJ5RB7jtg2G0lYCUgu7/z8PBYXF+FwOKBWqyEUCimJxG6349SpU3jjjTfg9XpzPeSrQJxopFLjuXPn6M+IwPJ4PBQXF4NlWbS2tkIul0MqldKMJSJ48/PzmJubw9GjRzEzMwOr1UpVYmKbXksgryekNxLedenATqrnC4VCmjZ2LRC7JxaLwefzIRKJ3BE7hM3jbt0EmVAV1zrP//vbGZkrse9IZktHRweMRiM0Gg1cLhcuXLiAyclJ2Gy2jHKF13NNyRy1Wi3EYjGlLV7p0SXNvAhdNb06yu1yEq43z3UR2FwhXwU208iFwBJwuVzw+XzU1dVBq9VCq9XC4/FgfHwcbrebMqAyhU/6mhYEFp+ceQLZmyuJYRLiCPFJZNrr/Ulf09wUCSrgY4d0m+5mTLYCbh8FgS0gY0i319a7I8EnBQWBLSArKNyu2cHV8ZUCCiggb3FDp1MBBRSQXyjcsAUUsIFQENgCCthAKAhsAQVsIBQEtoACNhAKAltAARsIBYEtoIANhILAFlDABkJBYAsoYAPhhtTEbGU8XKs8aKZqGafj457ZQb7HVCq1ZuIuwzDs7XzPmc7hvR38XwXKj/WaElxv7+bFDZsNYc13ZIIcf5uJ0bf0+SvLmeYSn7Q9ci3khPyfvvifVGElXb3zqbj2lSAVF0iSOqmsUEDukDOBvbKQ1ScFZO4CgQAsy1IByDehJYcqqbkrEAhoBcgCcoecCCypIAjk30bNNtKbaJHKfFcWqb7V52UDDMNAJBKhq6sLAOD1emkFywJyh5wI7CdNSK8FUpkhvd2HTCYDj8dDMBik3dnTD7f1Bil+TqpcOhyOnIwj10gvLJ6OK7sArAcKCew5ALFdSSlNvV6PsrIy7NixAzqdDv39/bDZbLBYLAgEAhnpK3qrSKVStIq9QqGA2WymXek+SSBaEGnwTUB8L+ktR9cD6yKwZGMS5wUJ45Ciyp+ETZBeoCy9sRTLsg08Dx0AACAASURBVJDL5TCbzWhoaEBJSQkMBgO8Xi+2bNkCj8cDt9uNEydOwOVyrZtKSgqgu1wuxONxMAxDG1HfznpxuVyIxWI6z+XlZXi9XoyOjma91++tgmg8ZN+SrgYSiQQikQgMw9B1YBiGVocMh8O0qn+2kHWBJSeTUCiktV1JRzfSS+ZOmj7nO9L7yJIesqSoOBFcpVKJmpoatLS0oKamhnbIS6VSsNvtWFhYwOLiIuLx+LretslkEsvLy7STXiQSuS2B5XK5EAgEUKvV6OnpwZNPPom+vj5MTU1hZmYGfr8/r3oKkb1K9q3RaIRKpaJlXPl8PjUP+Hw+rFYrFhYWsLKyQvd0ti6irAmsXq+HXq/Hl770JZSUlEAsFtOO46SXjNfrxfz8PE6dOoWZmRnY7XZqt210cDgc7N+/H42NjWhpaaEF1N1uN1wuF15++WUsLCwgGAxiZmYGR44cgVwuh8PhwJYtW+j3pdVqIRKJ8Nhjj2FwcBAvv/zyujWWSqVS8Pl8tEdQMBhc0++Rm6mrqwuNjY3o7OyEWq2GwWCA0WhEaWkpSktLEQwGsWPHDpw6dQr//u//nuXZrH3cRqMRRqMRCoWCtj7VarUwGAxQKpUQCARIpVL0MiLN0KxWK7xeL+bm5rC8vIyFhQXYbDbabT0TyLjA8vl8yOVylJWVoaKiArt27UJVVRXtvcIwDDweD63qPz09jWAwSNUQl8uFSCQCv9+/YW9dsVgMuVyOjo4ObN26FXfddRf4fD4SiQRdxNdee43ahB6PB7FYDKOjo+ByuaioqIBaraaNgRmGgclkwtLS0jXbnGQL6XFihmEQi8XWtCakF2p9fT22bNlCbXOtVkvDRVqtFizLwmw20/aL0Wg0p13uiL0qk8mogGq1WtTW1kKn00Gv10Mmk0EgENB1IU2r4/E49Ho9vF4vjEYjbDYbFAoFgMvOOrvdnpGLKOMC29zcjOeeew7t7e2orq6GUqmktls0GkUwGITX60U8HodarcamTZuwefNmhMNhRKNRnDhxAhcuXMCPfvQjRCKRdVGVMl1Hd+/evfjKV76CtrY26PV6CIVCarOSFoc+n4+2GyQe4V/+8peQSqV49913sWXLFjz33HPgcrmIxWL4wx/+gMHBwXXf0KSPTjQaXZPpwufz0dTUhKeffhpdXV20WTKxCdM9rRwOBzKZDLW1tXj88cdx6tQpXLx4MdtTui6I6SKVSqFWq9HQ0AC9Xo/y8nKIxWJ66SSTyVU3ptvtht/vh0QigUajwV133UVNhzNnzuDixYt44YUXMtJjKCMCSxwKXV1daGtrQ3NzM8rLy6HVahGPx+F0OnHmzBnaei8QCCCZTEKhUNATTKPRQKPRoLGxEQzDoLOzE3Nzc5iZmcnEEG+KTAgrwzC0UW9tbS2USiUAwGKxwOv1wuFw4NKlS5idnYXX613Vc4Y44WKxGGZnZ6HT6TA+Po5oNEo7zzudznXXOsjfu9nBSW4nvV6P0tJS1NfXo6ioCHK5nG7eZDK5qjs9+T2yya1Wa84FltisNTU11F6dmZmhzqT07594iYnDSSaTwWAwoLy8nPaaraysRCKRoJfWneKOn8LhcCAWi2EymfCv//qvMJvNMJlMAC5PyO/3Y2BgAF/4whcQDAZptzaiHre0tOCLX/wi7r33XrS3t6OrqwtmsxlcLhdvvvnmughspoRAKBSirKwMVVVVqK+vRywWw8rKCn72s5/hwoULOHXqFOLx+HVvKtLNbn5+Hnw+H4cPH6a2/dDQEHw+X96aCRwOB0KhEM3Nzejo6MCmTZsgkUjA5/OpDQyAsqbSb9ry8nJ88YtfxMDAAN57771cTYF2le/s7MQDDzwAn8+HpaUlHD58GDabDbOzs/D7/XQ+6c5DDocDpVKJ9vZ27N69GyKRCFwuFw0NDZDJZHfcI5mO8XZ/kWEYlJaWorq6Gt3d3aisrITZbIZCoQDLsrDZbFhcXMRvf/tbXLx4kbq8CdJb9b322mvQ6/Uwm82Qy+WQyWRoa2vDwMBARia5HuBwOCguLsbf//3fo62tDYlEAq+88gr6+/tx/PhxOJ3OGworOd2JNzWRSKC3txfLy8twu91564zj8/kQCoXYvHkzzGYzdu/ejYqKCtrpLR6Pw2KxYHl5GWNjY2hsbMSWLVugUCioI47cziKRCDKZLGdzlclkqKurQ0VFBQwGA4aGhjA+Po7+/n74fD74/f5V7SPJHiYCGwqF4Pf7sbS0RA+wTCdN3JbAEi6syWRCV1cXHnnkEdTV1UGlUgG47P6fm5vDyMgIfvnLX173lmRZFisrKzhx4gT27t2LQCBAY15msxk6ne72Z7bOIFrGY489BrFYjEQigbfffhtHjx6Fx+O54c1I4tNyuRxisRgajQaxWAxjY2Pwer0IBoPX7TGaS/B4PEgkEiiVSnR1daG9vR333XcfXcNEIoF4PI7x8XFMTEzg2LFjCIVCaGhogEgkWtV6lCRESKVSRCKRnAisRCKB2WxGUVERVCoV5ufnMT4+jsnJyZv28WVZlpp7Ho+HmkMEmRLaWxZYHo8HlUqF7du3o6OjA9u2bYPJZAKXy4XT6cTIyAheeeUVTExMYG5uDouLi2t6LvEM6/V68Pl8qk7lO8hG+9GPfoTOzk7I5XKEQiG43W643e4bqrHkZmlpacHWrVvR1tYGuVyOoaEhTE9P09hrPgqrVCpFQ0MD9uzZg8cffxx6vR5SqRQKhQIMwyCVSsHv98PlcuGPf/wjJiYm6IZO55Gn0/5kMhn0ej18Pl9OGl2bTCb85V/+JSoqKhAMBnH69GlYLJY1Oz5JWEgul0MoFK76WabW75YElrjji4uLKStHIpFgZWUFLpcLy8vLGB4eRn9/P+bn5+F0Otf87EQisSrVLB/yL9cCEl9sbW1FfX09uFwuVlZWcOHCBbjd7usutkQigUQigclkQmtrKzo6OtDU1ASJREI7m99Ihc4FiN9BpVJBp9Ohs7MTHR0daG1tpV5gIqizs7NYWVmBw+HA9PQ0nE4nVCoVBAIBeDzeVeGpVCoFLpdLn5MLEO50MplEIBCA2+2+qXaUDh6PB4FAAKFQSJ1MmW65ebOKE6v+XyAQ4P7770d9fT12794Nv99PiQ/T09M4deoUQqHQbak04XAYPp+PTi6fNuqNcO+992LXrl0oKyujp+qxY8fwwgsvXFe7IM6I+vp6/MM//AN0Oh1V/wOBAMRiMRiGoUkAuUR68jrZkPfddx/a2trw3HPPQSKRUNWWZVmEw2GcOnUK//zP/4ylpSW43W4kEgmoVCo0NzfDbDZDo9FQ7YnYgUSTIO/lAoFAABcvXoRer4dIJILL5bolsohCoYBarYZKpaJsNWLXZkrFv6nAEqEVi8WQSqUwGo0wGAwQCARwu90YGhrCxYsXKaOD3Aq3CpVKhZKSEvD5fMTjcaysrMDv99/erNYBZAOXl5ejs7MTYrGYnswej4dycAnEYjG0Wi1aW1tRXV2NiooKFBUVwWQyQSKRgMfjUS3jwoULmJqaWhX2ySXEYjF0Oh1aWlpQXV2Nrq4ulJWVQSqV0pvE5XLB5XLhzTffxPDwMN0PhNaYTCapmnvlLUpivX6/Hx6PJ2c0xUQiAZ/PRzOo1pr7S3wQjY2NaGhooHx5om243e71UYkJk4PYFxqNBiaTCXq9HgzDYHFxER9++CHGxsbgcrnuKLlZr9ejqqoKDMMgEAjAZrPB4/Hc9vOyDeLVrauro4HyaDQKp9NJA+lk46UTBL74xS/ioYceglAopGohSQxPJBLUdpqfn88bfq1UKkVtbS2eeOIJ7Nu3DyqValUSRyqVwsLCAiYmJvDtb38bKysrV21Qchilx2LJ7ycSCaqCOp3OnNivABCPx+HxeBCNRsEwzJq+f3Jwi8VibN68Ga2trasE1u12w+FwZGwtbyiw6Telx+NBOBzGq6++CqlUCpFIBIfDgfn5+VWq7K2CnGakAgUJCX3jG9/ApUuXbuuZ6wGi4hkMBrrxbDYbvvvd78JisYBlWeqA+MIXvoDq6mp0dnbCbDbTjA/go2R+QvQnsb5IJJLjGX6EsrIyPPnkk+jo6KDMNZK8ceTIEbzyyivweDzw+/3XdbKFQiEMDQ2ho6MDiURilUPRZrPhD3/4A0ZHR3PmIQZAIxb79u1DW1sbysvLEY/H4XK5qImmUCggEokoz7ikpAQymQwymQz33XcfSktLweFwaKz21VdfxcmTJxEIBDIyxhsKbPoXT+r5jI6O0tMn/UX4preapSCRSCgjBgAlG5w8eTKvqxtIpVJKvQQ+Yir19fVheXkZAoGAMl+2bduGuro6tLe3X7P6YDpjxuv1IhqN5uyWuRLENmttbYXRaKQ0y2g0ivn5efT19eH111+/qfoej8fhcDjoxk2fu9frpbHaXGoVkUgEi4uLYBgGBoMBZrMZyWQSUqmUjkulUkEmk1Gud2VlJeUOVFVVQaPRgMPhUAru0NAQ+vr6MuaLWLPAkn9f66RIT6EjPMu1CK5IJMLOnTvx3//939BqtQCA4eFhDA8P5439dj1UVVXhb//2b1FWVgbgIy+nwWCgh9CnP/1pNDU14e6774ZMJqNVJgCsUpcJa4bYv+nMoFyCBP+1Wi3q6+shEokAXB77xYsX8bnPfQ4Oh2PNm5GsKdGoyLNWVlZw/vx5LC8v53TNCXlDKpVCq9Xie9/7Hg1RkXVL927HYjF4vV6qcRKyCJ/Px7lz5/DLX/4SFosloymRtxyHvd4f5vP5qKmpoUW7HA4HTb4mC0XsYZVKBblcjvb2dvT09MBkMlE1a3FxMWOZDdkESWxOD/5LpVJ0d3dTW62trQ1ms/mqzxGk3zKxWAzz8/PU2ZQPIDeNRqOhrJ1EIgGLxYL+/n4sLCysWQvi8/koLi6GWq2m9iux8VwuF9xud87NAGJPA6CpjcQevVIzSiaTND9YLBZTn0QqlYLH48HCwgLGxsYQCAQyeghlLFtHJBLhwQcfRElJCSoqKnD8+HH09/fj3Llz8Pl8NH+Qx+Ohrq4ODQ0NeOGFF6DVaulmTiQSGBkZwcjISF7frsBHaiwZJ8MwKCoqwt/93d/ReCIhgF9pKlw5t1gshkAggA8//BCnT5/OSUmYa0EgEFCvNrHTI5EIDh48iL6+PsrAWgtkMhm2bduG6upqar/GYjHKJLLb7TmfcyKRoM5Csm7XSmck3wXxUZDYMgAEg0FcunQJw8PDOH/+fMbHmBGBTaVSiEQiVFdvbW1Fc3MzlEolNBoNIpEItFot9Ho9TCYTDAYD1Go1FArFqrIpiUQCly5dwqVLl3K+eDeDQCCgyeXAR95CohaRF7lNrgQR4Hg8ThP57XY7nE5n3mgXxGRpa2sDwzC4dOkSrFYrBgcHMTU1teZxMgwDvV6Pxx57DPX19QA+Mq8OHjyICxcu5MV6Ey/92bNnweFw0N3dDY1GA51OR9cyEAggHo/TYgwkJMflcsGyLJxOJ1588UVYLJasjDEjAktUuvHxcahUKvB4PBQVFUEmk4HL5YLD4aC2thZVVVU0fQ4AvXlIjC4cDmNubg4LCwt5sYA3AuFTk8JchAUkFovp/6fjypxbckBFo1F4PB7Mz89jZWWFaiO5BrFfOzo66A1rs9nQ39+PyclJLCwsrPlZEokEer0eO3bsWOVcdLvdeOutt9ZMX802SDx4eHgYwWAQYrEYJSUlSCaT9BZ1Op2IRCKUhqlQKKgwE3X4jTfegM/ny8oYM6YSk7Qwt9uNwcFBqlKIRCLU1NRg//790Gg0VIDJhg0Gg1haWsLp06cxNDSE0dFRmuhLNn0+FmobGhrC888/j8997nPYvXs3fT+9T1C60KYfTIlEAi6XCw6HA8ePH8fExAQsFgvGxsYQCoXyYq5CoRAymQzl5eXQ6XRIJpM4duwYDh06tOZyp4Tq98ILL6CjowNyuZxm8Py///f/cPz4cbhcrryYL/CRwI6Pj8NqtaKvr49mI6X1MQLDMCguLsbdd9+Nb3zjG/T3yWdIYYJsIKMVJ6LRKL0xSBkNtVoNvV4PuVxOM/YJYrEYXC4XRkdHYbFYMDQ0RNlS+Q6v14vBwUG0t7ejpKQEWq0WQqEQQqGQlrtJv02J9zwSiSASiWBychI2mw1DQ0OwWq2Ynp5eRYzPNaRSKZRKJXWosCwLt9uN+fn5Na+PTqdDUVERWltbUVdXBx6PRxlNIyMjGB4ezrtOAqlUCqFQCKFQ6JrEHWL6+P1+VFZWrnJIpZc8zdYhlJUibMSmJd5Sr9d7VToVqch39uxZ/Md//AcWFxdpPaeNwCMmm+4nP/kJ3njjDTzxxBMwm82ora2FQqGASqWiwpdIJBAKheB0OuFwOOB0OvE///M/mJqawvT0NC0Tk09zrqmpQVNTE+U1k4oLtyJg+/btw/3334+WlhZoNBowDAOr1YozZ85gdHQUi4uLeTXntYAcvqTET/oFRAQ9m3PKeplTpVIJpVJ51c3q8/lw+PBhWCyWVZXlNoKwAqvr9iYSCfz5z39GZWUlzYslBbiAy5qH3++HzWbD8PAwJicncenSJTgcjryds0ajQVFREW0lcjsMJIFAQPnG6WywEydOXJO+uFHA5XJRXFwMjUZD30smkxgcHITFYsmqlpRVgeVwONDr9dTLRoQ2Go3C4XDg5z//Oebn5/PKjrkVsCxLSe+Li4uorKxEXV0dBAIBSkpKqFMtEonA7XZjenoaH3zwAU6fPg2Hw5F36mA6ioqKUF5eTpMSSL2pWwHJ7kmPu05PT+Ott97Ka574zUBqNZlMplVEmA8//BB9fX1ZJb1kTWCJy/uzn/0s2tvbqdubZVm8//77GBgYwOLi4oYuZ5qOeDwOm82GAwcO4DOf+Qw6OzvpIaVQKGjVfq/XS8kk+QyPx0PL2vD5fEil0muSP64HDodDc31JAfVYLEa/g43gp7gSHA4HarUaRUVF+PznP4+6ujr6s2QyiRMnTqC/vz+rN2zWitzKZDIYjUY0NzejoaEBAGg5z4mJCQwPDyMQCOT1LXMrINTCoaEhzM3N0XmR8A/hl95uvvB6g9AkiWAJBAKoVCoYDAbK/rkeSBVNtVoNnU5HWWxk/sQM2CggmVkKhQImkwmVlZVoaWmB2Wym7C8SkrTZbBvPhuVwOHjooYdw//33o6mpiZZNWVhYwNTUFI4ePYq+vr6cU9EyDaL+zs/P49y5c2hra4NOpwPDMLR65PLy8obYrBaLhWbfkJ4yf/3Xf41du3bha1/7GiYnJ6/bjNpgMGDLli0wm81UuAOBAE6cOJG3pJgrizUQcLlcKBQKNDY2oru7G3v37kVVVRVKSkqo93x6ehpTU1MZpyFeCxkXWA7nctdunU5H67PG43GaLzkwMACbzbYuk8sVSOe39PmFQiHMzc1lLM0q2wiFQvD5fAgGg4hGozQBn2EY7N27F42NjYhEIjSuTOiUCoWCalYlJSWr/Bbz8/MZKaadKZCaWqSDIPn/RCKBZDIJoVAIqVSKqqoq1NXVoa2tDZWVlVdlLU1OTuLs2bNrrk5xJ8i4wBJ6ntFopE4Lr9eLkydP4vTp03j77bdp+ObjCpLjm35Sezwe9Pb2bhjbLRgMwu12Y3l5GXK5HBqNhpY/+d73vrfKJvX7/VhYWKC0VFIln9jwyWQSoVAIIyMjt8SQyiYIT5i0Vdm+fTutWun1ehEKhWhFkIcffpgWuidxV4ZhEIlE4PF48Kc//Qm/+MUv4HK5sj7ujAsssV9I9j7LslhcXMSJEycwMTEBv9+f9w6XO8X09DTeeOMN8Pl8FBUV4fe//z36+vryPmUwHaQR1o9//GN0dHTg8ccfh8FggEqlopv9ys6EqVSKtuVgGIbevqQFx5kzZ/KChki0QJFItKqeMinPSmxskphO7PBwOAybzQaXy4WRkRE4nU7MzMzg7Nmz69aBL+MCSwz0WCwGj8eDUCiEmZkZDA4OwuFwXFVQ/OOIxcVFnDx5Es3NzQiFQvjVr36VVyVf1gKSkH/48GEsLy+jo6MDwGXvP2nFyOPxaHkUUkCeMH1IY6twOIzz58/DYrFgdHQ0L5yMhK0kEomoqrtp0ybI5XLacZ58BrjsLI1EIvD5fJicnMTs7CyOHDkCm82G0dFRqkKvy9hvdOJzOJxbvg6kUimKi4vR1NSEsrIyWK1WrKysUBraejJ6WJZdU73M25nnjUDULNJXZmFhgdZsygbWOk/g9te0qKgISqUSarUazz//PKqqqlBWVkZpmH6/H36/H8eOHcP4+Djef/99xGIxWkEkHA5npBhZJtaU9EBSKpVoamqCTqeDSqVCUVERNm/eDJlMRosOulwuHD58GNPT0zS/NRqN0jackUgkK/v5evPM+A1LUsYWFhYQDocxOztLaVz5yOjJBuLxOAKBAFZWVjbUrXo9kBxP4oTp7e2Fx+PB8vIyvWUDgQB8Ph/6+vowMTGB/v5+xOPxvDV/iGNwaWkJwWAQ8/PzcDgctHsdaT7ucrkwMDAAq9WKiYmJnO/hjN+wxPNGDPP0TuPrjVzdsOuNbN+wV4KUeLkyFktUYvLfbCCTa3qt9pckXZL8O13NX889fL15Zlxg/+/3VmUw5AoFgb0an5S5flznmRXiRD7mrxZQwMcBWaMmFlBAAZlHQWALKGAD4YY2bAEFFJBfKNywBRSwgVAQ2AIK2EAoCGwBBWwgFAS2gAI2EAoCW0ABGwgFgS2ggA2EgsAWUMAGQkFgCyhgA6EgsAUUsIFwQ/L/Rs14SMsU2nCZHSS5WiQSQaFQ0F49JLeUtIPw+/10npFIJOfZOld258sWCtk6HxOQ3MWNDi6XC5PJBKPRiIaGBloYjCSIj42NYXl5Oe9qG5OUyvQxfRzWI9/wsRFY4KNT/kZFrvMZCoUCOp0Ozz77LIqKimAwGGjvUdJMi1SljMVi8Pv9Oa+RRIqx6fV6CIVC2qXP5/PRWkcFwc0cPhYCm54wTzbHRhRapVKJsrIyPPzwwzAajRCLxbQOlt/vx/LyMqxWK+2pG4vFcnrLkkJlQqEQBoMBcrmctpMkdYpzXVIl21hvze5jIbDpCfPpJWo2CrhcLgQCAb7yla9g+/btMBqN1G69dOkSZmZm8Kc//QlLS0uw2+3wer1YWVlBKpUCn8/P2ZgVCgW6urqwY8cOGAwGAMA777yD2dlZzM3NfSxvV3I5kNKuGo0Gbreblu/NdvGGj4XApoN8YRtFYHk8HoqKilBRUYHW1lbU1taCy+XC6/ViZmaGdgMfGhrCysoKbQgdDodzNmYOhwOpVIrm5ma0t7dj06ZNEIvFCAaDiMfjq1poflwElgiqQqGAVCpFWVkZZDIZtFotPB4PFdhUKoVUKoWVlRUsLi7S9zIG8qVe6wWA3civG80tH+bJ4/FYg8HA/tM//RPrcrnYaDTKxuNx1uFwsL/5zW/YmpoaVqvVsgKBgOVyuSzDMPTF4XBYLpfLcrncNc8zU3Pl8XhsR0cHa7FY2KWlJTYej7M2m409efIkW1ZWxvL5/I/dmvL5fFYqlbIPPPAA+7WvfY2dnZ1lfT4fGw6H6SsUCrF+v591uVzsD3/4Q7a8vJwVi8UZnWfOb1iGYWgfUR6PR6vUbZQeNLcLPp+P4uJifOYzn8H27dshk8nA5XIRjUZx/vx5DA4OYmVlBaFQ6LqOpVzYrxwOBxqNBgaDAVqtFjKZDAzDYHh4GENDQwgGgxu+tGt6Ow4ulwuRSAS5XA6VSoVkMgm73Y73338fZrMZ3d3d4PF4tNoiy7JIJBLo7OzEl770JRw9ehRTU1NwOp0ZWa+cCixxWkgkEhq+IFXjP+51jMViMSorK/H1r38dCoWC2qKRSATvvPMOhoaG4Ha7b/iMXHw3HA4HBoMBJpMJKpWKNoX68MMP8cEHHyAYDOZVuOl2QIRVKBRCIBBAo9HAaDSirKwMi4uLmJiYgMvlwpYtW9DU1ASpVEoFlrQB6enpwZYtW6iZ4Ha7N67ACgQCKJVKfP7zn0dJSQlqamooQSCVSiEcDmNmZgbvvfcefv/733+shJZhGIhEInz9619HR0cHFAoFbQkBXO7ydvLkSVit1twN8gbg8/l48sknsWnTJvD5fCQSCUSjUYyPj8NisWyYZl/XA4fDgUwmg0QigVKppM6lWCxGY+DhcBhWqxVTU1M4e/YsnnjiCezcuRPFxcW06TVpiPbUU09h27ZtePbZZ7GysnLH41s3gSVNsqRSKaRSKXQ6HXp6elBVVYXm5mZwuVxwuVwkk0lEIhHMzs7C4/Hg1KlTcLvdiEaj6zXUrIE4LTQaDXp6etDS0rKqq3k0GkUgEIDNZoPD4cjhSK8NohE1NTWhsbERDMPA5/PBbrfDbrfD6XTmeogZAZfLpc2y+Hw+uFwugsEgPB4P3G43bc+xvLyMiYkJ1NbWorKyEhqNZtV6cjgcNDc3Q6VS3VL3+hviVg13DofDcjgclmEYlsfjUYcIef9avyMQCNjS0lL2b/7mb9gPP/yQnZiYYBcWFthgMMhGo1E2lUqxqVSKZVmWTaVSbDKZZGOxGGu1Wtn33nuP7enpWXcHBZnP9eZ0qy8ej8cqFAr2+eefZ9966y3W5XKxiUSCTcfJkyfZF198kVWr1VmZ5506Y4RCIavX69njx4+zPp+PjcVi7IEDB9iysrLbdq6Q75rL5bJ8Pp8VCATUqZbpNV3ri4xFKBTSF5/Pp/v8ys+XlJSwd911F3vhwgU2mUyyV2Jubo41mUy3tJcy5nRi00Im5MQl3cwkEgkEAgEkEglVcUmvUJPJhC1btqCyshJKpZKeOCx7uSkuYfSkv9RqNQBQx8ZGto1EIhEMBgPKy8tRXV1NvzMA8Pv9cLlc6O3txdDQUM7ZS9dDWVkZampqoFKpEI/HMTY2hvHxcSwuLt6yo4mssUAgoJ3wkskkfeXSDCKhGYKbjYV070tv85Et3JZKTCZA5tDYUwAAIABJREFUeoMajUYolUpUVlZCp9PBbDbDYDBArVajrKwMcrkcRUVF4PP54PP59LSIx+OIxWIIBoNUsInzhdgSIpEIUqkUfD5/XdXiTG4YhmGgVCrR2tqK+vp6VFdXg2E+SpSam5vD2bNn8dJLL2FgYCBjfzfT2LVrFx5++GGYTCa43W78/Oc/R39//201vBIIBNShQ1o/ko7vsVgspzHcW/27DQ0NuOeee6BQKK4b/8/UfG7bhiUDII1vjUYjdu/eTT2IIpEIQqEQiUQCfr8fc3NzmJubw+TkJPWcpQeV77rrLrS0tKChoQESiQQAKC81n7ug3Qjpi8fn86HT6SCRSFbRKGOxGIaHh/HKK69gfn4+V0O9KRiGQVFRERobGyEQCBAMBtHf33/LYxYIBBCJRNi6dStKS0tRV1eHSCQCm80Gi8WCqakpAJk9MLMFwqq7EbPO4/FkLKQD3KHTiagOQqEQKpUKnZ2dMBqNMBgMSCaTSCQSsFqtcLvdGB4exrlz53Ds2DG4XC5EIhEkk0l6S7MsC5VKhaqqKiqw8XicCvdGiu1dKwlBKBRCq9VCJBLR95LJJHw+H8bHx/Huu++u+zjXChLm0Gq1KCsrA3A5/DQ5OQm/339LzxIKhVAqldi0aRPa2trQ0dFBzYHFxUXqHd8oAkvabQoEgmt280unkWYCdySwxKPrcDgglUrBsiwYhgHLshgbG8Pk5CR++tOfYnZ2FsFgkOZxpt+s5BklJSXYtGkTpFIpfX5vby/++Mc/YnJy8s5muc4gm43Y+xwOB6WlpXjiiSdQWlpKF3Zqagr/+I//iImJiVwO96YgMUmytuRGuZUm1RwOBwKBAM3Nzbj33nvxF3/xF6iqqqJ9WKPRKM6dO4d4PL5hfBUikQh6vR5bt27Fgw8+CJVKRX9GLqze3l4MDAxkzJy7I4ElKnEoFILP54Pb7Qafz0c4HMbFixcxNDSECxcuwG63X/eGJKq1WCyGSqVaxRhxOp2wWCzw+Xx3MsycgzjkSkpKIJPJAFzWTgKBwJoIEvkAkpVC1vxWhYrc0iqVChUVFdDr9XSD83g8GoPfKKZPusNVrVZDp9OtiqcT38z09DQmJiYyNq+MCKzH4wGHw8F7770HgUAAn8+H48ePY2hoiDZ0vhlIxkp6X9n5+XmcOHECkUjkToaZcxAvokajoc4mom04nc6cEvnXAuIgJE5C4tknMcq1CC8RWJlMhqKiImoaMAxDO6H7fD7KcMtHpKu8ROvQaDQQiUSrGlynUik4nU5MTk7ijTfewOnTpzO2hzNCnCD5mufOnQOXy0U4HMbCwsKawhPEcCd8TA6Hg1AohLGxMczOztLMj40KoVCI7u5uNDQ00EVNJBJ488030dvbuyFuFEK3S3eukBsm3dt9I5DDPZFIIB6P099nWRZ+vx/Dw8NwOp05D+mkg8yVcIr5fD4dH5/Ph0KhgMlkotRSooVEIhGMjo7i8OHDmJ2dpYdcJnDHAks8nfF4HO+//z4l7691gITClU6g9vv9OHnyJCYnJzfEhr4RRCIR9uzZg46ODroB4vE4Dh48eNshkfVGeryUzIFsYB6Ptyb7jJDi4/E4IpEIXfdEIgG3243Tp09jYWEhrw5n4n8gSfqEosiyLIRCIdRqNcxmMzQaDYRCIQAgkUggGAyit7cXL774YsbT6zJyw17BMLml06SlpQXPPfcctm/fTt9zOBx4+eWXYbPZMjG8nEGn06G0tBQ7d+5EeXk5fZ9lWfh8Pvh8vry5TdYCIqThcBgikQg9PT0YHx/HyMjIqvzXa82J2PHl5eXYunXrKgeNz+fDhQsX4PF41nM6NwRxkvH5fEoIEovFKCkpgUqlQklJCcxmM3bs2LFqbW02G773ve/RwzjTB1BGucS3uvlIitmuXbtoxQJyQo2MjOS9bXc9EM50eXk5KisrUVFRAZ1Ot+oz0Wh0w/Gj00vxiMViNDY2IpFIwOv10vpN0WgUiUSChu1SqRTd/Hq9HkajEcXFxdSGJVGClZWVvEocSI+xEmElAltcXIy6ujqUl5ejvr6e3q5erxfz8/M4fvw47HZ7VrSFnKXXCQQCNDY2orm5GWazmdozCwsLsNlsGza1jsvlYs+ePXj66adRU1MDjUYDvV6/irZGbLmNElsmDiOSmSORSFBVVYWvfvWriMViiEajcLv/f3tXFhtndbaf2Zdv9sX2eLzvdkyiOHFsR2FpIpYCERQuKEK0BYWbqhdVJaiq3lRqK6QCUsUFRSqiTRAtVagSaAs0EYshCTh27HhiE+/rjGexZ/1m86z/hf9zMjZOsJ2Z8Td0nqsotme+5bznvMvzPq8XgUAAIyMjmJycxMcffwyPx4NAIAChUIiamhq88MILaGtrg1wup59ns9ngcrl2XZ9qI1KpFOUJkGRZaWkp9u7di4aGBnR2dtKWUD6fj9XVVbz66qsYGhrC5ORkzjafnBssoZ1VVFTQIjPp3Nm/fz/a29tpwJ5IJDAwMICBgYGCWcyZkMvlaGhoQFtbGxobG2kZJzP2203K3U6RGX/GYjFIpVIIhUJoNBqaTFIqlQiHwwBA3V2Px4NgMAiBQACTyYTGxkYYDAb6roPBIC5duoSRkRFOPhNSR5fJZNDr9aiurkZlZSVNNEkkEvB4PDgcDjidToyOjmJqaiqnteScGiy5WbPZjKeeeor2GcrlcigUCnR3d0OhUNDFHIvF8Nprr2FoaIhT7tFWYTAY8KMf/QgHDx6k7Wcb2S+E3F5IIG5rKBRCMBiEQqGgmy8BcQsrKiqQTCbx6KOPIhKJ0HKGSCSidXbS8+xwOPCHP/wBVquVkwabSqUgEAhgMBjQ1NSE7u5udHR0oKysjLLxUqkUBgYGcPHiRXz++edwOBw5vaacGSyJAaqrq9HY2IjOzk6o1Wr6skUiERQKBc0UxmIx+P1+sCyLUCiUq8vKKbxeL95//32k02m0tbVBIpHQDCNxK0mJoJBARMcMBgNkMtmmvNmN7C6RSAQ+nw+ZTAbghhSQy+WC1WrFp59+ivHxcdjtdnoycw2pVIpqLtfW1qKjowMGg4G+T1KfJjX1fGzEOTVYcrOVlZVobm6GVquFSqVat5uSeI5lWbjdbgSDwYJLxhCQclRtbS2cTicUCgXlzpIFTAyWnL5cPFk2QiaToaqqClqtFhKJBKlUCrFYbN0CJS4gWeSE5J9Zp02lUvB4PBgZGcHZs2dhsViofjEXQRJmarUaJpMJDQ0N68IbwvhKJBJU4jTX2LHBkhdBxjNsvFhSj/36669pryP5HcJJJa6Ry+XC3//+d5w/fx4LCwu3cTu7j2QyiX//+9/o7++HWCyGVqvFiRMnaKKCZFpNJhMcDgfsdjtnFyyByWTCQw89RCVY+/r6MD09jdOnTyMYDFIFBmAtZ9HZ2Ylf/OIX0Ov1UKlUAG7EwX19fXjppZewtLS07u+4COItkN7taDQKsVi8bu1LpVIcO3YMe/bswcWLF+F2u3N6TzsyWLLDkAQSMVhilJlN7qR8kXmqZH4GKeMsLS1henq6YE/XTLjdbrjdbgiFQmi1WiwuLkKn09GfE6kYlUoFu92+i1f67SCdWE1NTVCr1UilUhgfH8e1a9cwNDSEUCi07pQUCoXQ6XRYXV1ddwInk0n4/X46vaAQSP7EtdfpdJDL5UilUrR2LhKJqFgDIU7U19eDZdmcxuQ7PmFJIZy8xFQqRVvhotEoPUmUSiXUajU0Gg2NZwj4fD59kaRNr5BcxW8DqUfOz8/DZDLR/+fz+aiurobb7cbk5CRnk1Aku9va2orvfe97dGbOqVOnYLFYEAwGv/GeYrEY7eLJ/FkoFMLg4CDm5uYKZlMmmfC7774bFRUVAEAF3c1mM4xGIxoaGigL7Gc/+xmuXLmC3/zmNzlTDdmx4gTJoMlkMtTX11OhKZKuJz2sRGEh05Ugn0GMm2VZ8Pl8qFSqdR0bsVgM0WgU4XC4ICh8m4F4HhuNUi6Xf2MD4xokEgmOHDmCvXv3QiAQ0AFcoVDopu6sRCKBXC6n6yGdTsPtdmN+fh7vvfceLBbLLtzJziCVSiGVSpFKpWCz2TA3N4cLFy7AbrdDo9GgtbUVOp0OSqUSYrEY1dXVWFlZyenUiR2fsMRgpVIpuru70draiqqqKsoNZVkWq6ur6OnpoR0NmbVIoj8cDofh8/kgEAig1WqhVqsBrLkjLMvC6/XC4XAUrMECoIwfAh6PR8tbXB4pIpPJ8OCDD6KlpYU2Zfh8PkSj0U3LbiQrrFAoYDAYaMvc0tISLBYL3nzzzYI5Xck7kkqliMVisFqtGBkZwfnz5zE/Pw9gTTLnyJEj1A7q6urg8Xi4abCED0vcYblcjoqKCtrRQNrqtFotDdrJ73722WeYmprC559/Dq/XC7fbTY2cKFCUlJTQWM/n822rWZoryGwpI6oaJEk3PT2NmZkZzsdxG93a5eVlJBKJb4QtarUapaWl+NWvfoXm5maq3RWNRvHHP/6x4GrrpKnFZrPhjTfegM/nowQJ8s5mZ2dx8uRJPPLIIzhy5Mi6aQG5Cutuq6xDXKRAIIBwOLxOMC3zd2KxGFwuF3V3LRYLLBYLzp07R+NeAlIOyGQIZXJYCwmk9kh2auAG04kkpgopVifXLpfLwTAMkskkRCIRFeKrrKzE0aNHYTQawePx4PP54HK5cPnyZYyOju725W8b8XgcgUAAw8PDVKQhs9oRCoUwNTVFBRbIOiUJ1lzkJm5b0ykWi+Htt9/GhQsXUFdXB7PZDJ1OBx6Ph2QyieHhYYyOjuKVV16hNdZIJELj140nTDQapYLaG+tdhQaGYaDT6dDU1ESTFqS84XQ64XK5OG+wJO+QTqdRUVEBlUqF73//+5ifn0cwGER7ezsOHz5MedPk3a+uruKVV17BW2+9BafTuct3sTMQWSO/30/DuEwwDIOmpiZKxSTeoU6no32+2UZW+mH9fj9sNhs+//xzlJaWwmAwIBqN0vEGs7OzWFhYuGnss9lnbnR/C/GEFYvFdMqBWq1eJ7NSCN06ZKwIoR2KRCIwDIN9+/ahvLwckUgE9fX1aGxsRHl5OdXjstvtuHz5MiwWy440i7mCW/G+CaGitbWV6mcDa8nEffv2YXx8HGNjY1m/pqwwnYjCxG9/+1t6qrhcLjpiIxunI9dPoo0gSQu1Wo36+nqUl5fTn5HYrhAMVqvVQqlU0pqkUCjE448/DuBGjE6IMMBaKau/vx/PPPMMIpFIwRrrt0EgEKC8vBzHjx+nOl0AYDQa8cwzz+C9997jrsECa4swFArRzC8Zk1iIrmw2kE6n4fP5sLS0hIsXL6KpqQn79++H3W6HzWbjLH82E+FwGP/85z/R0dGBH/zgB3QkaCbTB1jLgrtcLiwvL+Mf//gHRkZGvtPGSjayTBYXASFQtLS0oL29HQsLC2BZljsSMQTk1ADwnZrtmlmK2i5IHD44OIhEIoGqqirMzMxgcnKyIJrzo9Eoent7EY/Hceedd4JhGNpaR4yW9I0Sptpf//pXrKysFFRGeLvg8/lgGAZisRiRSIQmR0nDu9lsRm1tLRobG+H1erM6M5d3q4X4/8N7ChbpdHpLgW8u71MgEFBqm1qtprHrVkXqtoKt3iewvXslXFnSvE2IBLW1tRAKhXS0BpG7CYfDWFxczCkRngvvFFjLTyiVSpjNZrS2tqKurg73338/ysrKUFZWBofDgdnZWfzpT3/C0NAQlpaWtmW0N7vPXZ/A/l1HMpmkoyNJ2p+oLXAd6XQakUgEkUgEKysrlD/r8/nWGSwhyXxXXeDNEIvFaGludXUVfr8fBoMBJpMJ5eXlNLu8VZnfraJ4wuJ/5z6B7Nwr2Xh2Irp3u+DiO91ImMik4BKK7nafUfGELSJrKESZm1ziZnzxXLCdtqYCXUQRRWwbudjUigZbRBEFhKLBFlFEAeGWSaciiiiCWyiesEUUUUAoGmwRRRQQigZbRBEFhKLBFlFEAaFosEUUUUAoGmwRRRQQigZbRBEFhKLBFlFEAaFosEUUUUC4ZbdOvluUMpENBtZWW7EEAkF6qx0omTpGRHmBz+dTBcjd6AnNd3vdbuH/NZ1z2l6XuQ4zZ0Rl/mwra4WsC6VSCYFAgGAwSPW6twJOt9dlag8TQS+y8PNBndyO7hR5WZlDv25HRqaIrSOXzzdz/ZHvIt+XuT4zxeZuBTIXuLq6GgqFAhMTE3TkzO3cx64bLBlz0NraipqaGshkMsTjcVitVjgcDszPz39j1MVug2jUJpPJ78zgrv918Hg8yGQy6PV6KBQKyGQysCxLh40LhUKIxWIqjE8mIGx890Rdsq6uDu3t7Thw4ADkcjnefvtt2O322x5WzhmDbWxsxKFDh6BWqxGNRunQJJvNxiljBW7s9Jku8Eb3qYjCA5nnazKZoNVqsby8jGg0imAwCIlEAplMhmg0img0SidWZKpJkGHWUqkUJpMJHR0d6OnpgVQqxUcffUQnBNwOdt1giRvCsiwVnY5EInA6nQiHwxAKhZxU4CNue+a0veJJW7ggw8WdTieam5vR1tZGp/R5vV46kqSlpQU6nQ7xeByJRAKRSAQ+nw9+vx9jY2OIRCJ0at9nn32G//znPwiFQpibm8vKAOtdN1iy8D0eDxYXFxEOh7G6uorl5WU6bIvL2BjnZE6XL6KwkEgk6Awdj8dDJ1WQhCLxBlUqFcrKysDj8RCLxeD1ehEIBMAwDPx+Px2cZbPZ4HQ6bzmec7vYdRG2zIW+cRzl7WoH5UOwi1w/yRgLBAIkk0kkEokdiW/tBLnIEpN3QTYgrug45eOdkmFWmcOt1Go19Ho99u/fj/r6ejz33HPQaDSQSqX02aRSKdjtdpw8eRKXLl3C+fPnd7xxczZLTBZBvhZ3tqHRaKBSqWA2m6FQKGA0GhEOhxEMBjE5OQmPx5NV5fd8IlMNUCQSQaPRQC6X0/Gf0WgUiUTitjKfG8soXAARVCPXJhAIwLIsUqkUvv76a7hcLojFYrS3t+P48ePf+Nupqal1YymziV012MzhUIUKo9GI6upq9PT0wGQyoa2tDT6fD3a7HWfPnsXY2FhBT5Dn8/mQSCR0RlBZWRmmp6ep2xiJRBAOh6lHtF0IBAIA670qriCzhBMMBhEMBuF0OsHj8XDx4kUcP34cDz/88LpNJxwOY3h4GHa7PSfXlHeDJWryAoGADsraCdlgY/0z3y9ar9djz549eOihh9DT0wODwQCZTAaGYZBIJLC6uoqamhq4XC6Mj4/j66+/xtmzZzm1IG+FzOvU6/Xo6upCT08P2traaFxHppJ/+eWXmJub23IWlMfj0SmHjz/+ODQaDZRKJf71r3/h0qVL8Hq9nN7giMD6ZpMb4vE47HZ7VjLCmyGvBksybRqNBkKhEG63G7FYbMfsoN1yp/h8PjQaDfbs2YMDBw6gq6sLQqGQTlcnYBgGwWAQJSUlkEql6O/vpy6kz+fj9KLMhFgsRklJCWpra9HW1ga5XI54PA6bzQYAmJ+fh8PhuKXrT9xrqVQKuVyOqqoqmM1m3HXXXTAajdBoNFhYWMDi4iJCoRDnn81mOsTAWraZDIXLBfJmsDweD42NjTh48CA6Ojogk8lw8uRJLC0tYW5ubtufBdxwo/IJPp8PtVqNzs5O/O53v6NDkTIRj8exuroKhmGgVCpRVlaGnp4ePPvss7DZbLBarXjhhRcwPT3N6RM3nU4jHo/D5/NhfHwc+/fvRzKZpIOLa2traVZ0YWEBbrd700UskUhojfPw4cN44IEH0NbWhpKSEpSUlNCE3YkTJ/DAAw/g2WefzcmoxlwjH259XgyWz+dDJpOhqqoK3d3daGxsBJ/PR3V1NWKx2LYNlpAUdmOxSyQS3HPPPTh06BC0Wi09VScmJmjsGo/HEYvFIJFIIJVKsW/fPiiVSphMJjoU+d5770VFRQW++OILTs+kSafTiMVi8Hg89OQg10tq0CS0uRlxhGTRtVotSkpKUFFRAZPJBL1eD6lUSv9OpVJRA+Y6MqsawNqz6O/vx5UrV3L6PvPyZIRCIQwGA7q7u/Hcc88hlUqBZVkcOnQIADAwMLClz9mteS6Z0Gg0ePHFF1FZWUlfWDwexzvvvIOhoSF8+OGH1J3j8/nQ6/V45ZVX0NLSggMHDsBoNMJoNOLVV1/FwMAAjh49yunRk+l0mk6lI7VxhmEgEAgQiUTgcrmwsLBAR43e7DPEYjEqKythNptRWloKtVoNmUy27vdIyESMgcveh1AopGEQsDYc6+WXX8bg4GBOiT45N1ihUIiysjL85Cc/QU9PD00WxWIxXLx4cVPXh+zIBoMB5eXlEAqFSCaTcDgcCIVC8Hq9ub7sTWEwGGA2m8EwDEQiEVKpFM6ePYve3l709fXB6XSuK3GQjenUqVNobW3FysoK2traUFVVBYFAAIZhUF9fD6fTSSfccRHJZJISWmKxGPx+P5LJJOx2OzXkW8VsiUQCgUAAIyMjYFkW09PTOHHiBO644w5IJBK66D0eDxYWFhCLxThtrAqFAk8//TS6urro/6XTaTrNriBdYmKYMpkMJpMJDz74IMrLy+nOubq6ipGREVit1k3/ViwWo7S0FO3t7ZBIJHTXWllZ2VWDraiooG5cOBzGJ598gj//+c+bjhUk2cTz589jYWEBGo0GWq0WVVVVNFteX1+PRCLBeYMlxhqPx6nxLi0tweVyfetYRUI3nZubg8PhwOjoKO677z40NTVBIpHQ38sMKbgMmUyGBx98EE1NTfT/0uk0AoEAWJbN6XfnxGB5PB70ej0MBgOefvpptLa2orGxEVKpFADgdDoxPz+PQCDwDVeKx+OBYRg0Nzfj/vvvxxNPPAGJRIJIJIK3334bIyMj2455s3VPP/3pT3Hs2DGoVCpcuXIFL730EoaHh7c0A3R+fh5vvPEGqqqq0NnZCT6fj8rKSrz44os4efIkp5Ms6XQaiUQCLMvC7XbT2JNk+wkRfisJwFgsBpZlEYvFaIKGbOJzc3MYGBi47Y6WXEMoFKK1tRVms3nd/+ejqyzrBksyiKWlpaiqqkJzczNqa2shk8kgEAgoyTocDtMm38zgXSqVQq1WUyOvrq6GRCJBMBiESqWiRp9PiMViyOVyVFdXo76+HgKBAF6vF0NDQ1hZWdmSCxSNRrG0tISJiQlYLBY0NTVBJpOhoaEBTU1NaG5uhs1mQzAYzMMdbR8kYxyPxyESiSASiaDVasEwDI3ltvIciPGTz8qsoRMyPdd52Hw+H3K5fFfWYtYNVi6Xw2w249ixY+js7ERdXR3UajWtPyaTSYRCIUQiEWg0GhoTAWunmNlsRltbG37+85/DZDJBoVBQPmc4HL5lciNXMJlMaGlpgcFgoN1DLMvSXt3t4PXXX8e7776LM2fOoL29HSKRCPfeey9qamrw61//Gl999VWO7mLnIOUKQnJRKpXQaDQwGo1wOBwwmUybhjY3+ywACIVC8Pv9NNOeTqchk8mg1WoLIku8EfnaZLL6ZEiJg5RqeDwepqenwTAMysvLYTabUVtbC6lUCrPZjCeffBIsyyIUCtHCukajgclkQllZGRQKxToFAJZlEQ6Hs3nJtwSfzwfDMGhra8MjjzyC8vJypFIpuFwueDyeHb2kSCQCv99PCSOkrltTUwOGYXJwF9kDaebObNYwGAxobW3F9evX4XQ6v/UzSCZYqVRCpVJRY00mk5SfzOUTlmEYqNXqdVPWo9Eo5RrnGjkx2FAoBIvFgrGxMbAsC7FYjLq6Otx1112UIG80GnHHHXcglUohHo9DKBRSl5nUbTfWufx+f17jG1I77OrqwokTJ8Dn8xGLxbCwsACXy7WjzyS0vlgshkQiAZFIBJVKBYZhIJfLOVvOIPVYUoIiHGCTyYQDBw7gk08+2dLniEQiKJVK6PV66HQ6umYSiQRtDOeywWo0GhgMhnUGGwqF4Ha788LOyqrBkpfq8/nAsix4PB4SiQT4fD5CoRCWl5cxMDCAe+65Bw0NDeju7oZcLgfDMOt6STN5wgQCgQAGgwFqtTqbl3xLyOVydHR0oKqqir6gaDSKCxcuUEWMnYCcKJlqFVw00o2w2WywWCw4duwYNBoNBAIBVCoVampqoFKpqITKZiDSKYcPH8YjjzyCxsZGAGuJGqvVii+++AIff/wx+vv7c8bDzQaeffZZ3H333VCpVADW3t3p06dx9uzZLYcFt4OsG+zNOJaRSAQsy8Jms9HYtaKiAgaDASaTifYgAt9UUCTI/J18QCQSQa/XQy6X012f6E3dThlmo3ESL4PrRuvz+WCz2RAOhymTSyQSQa1WQ6lUQi6X00xp5r3w+XyapGpoaMDhw4eh1Wpp+LS8vIyrV6/i+vXrtA7LRfB4PLS3t6Orq4uqSqTTaUxMTKC3tzdn/OFM5DW6J3W89957Dx999BH+8pe/4PDhw3j++edhMpmoi7QR6XQa0WgU/f39mJmZydv1JpNJ2kbmcrnAMAyi0SitQ+5ULZFIpJLkis/nw9LSEoLBIKeNlpTi5ubmIJfLodfrkU6nwTAM9u/fj1Qqhb6+PkQikXUbkEKhQHl5OZ588kns3bsXVVVVVGxveHgYfX19OHPmDG3X4+oz4PF4VNuJhC5ks11dXc3LdefVYMmORLLE0WgUMzMzsFgsNF4EbpywRMd1cnISMzMzcDqdOS9MZyIWi8Fms+HatWtQKBSQSCSIRqOw2Wzw+Xw7ijclEgkUCgVEIhGNA8kJtFFKk2sgNdRLly5haWkJOp2OvqOFhQWEQiFIpVIolUoYjUYAa+9SqVSitLQUdXV1MBqN4PP5tL90YGAA165dg9frzdui3wnEYjFkMhlEItG6RGg+lUWAXWpgJ65zKBTCxMQETp06BZlMhvr6enrqEJYQy7I4efIkLl68iNnZ2by4HQTBYBB9fX0YHh7Gu+++u452uNMEA8mCk54FinXNAAAKDUlEQVTgdDoNqVQKg8EAuVwOgUDA2dayeDwOv9+Pl19+mbrCwA21QCKl0tTUhOPHj9MQRqlUgmEYmM1m6jYvLS1hYWEBr7/+OhwOB6fjVmDNSzCZTDQxCKwdKNFoNK/NG7te8FIoFGhqaoJWq6U7F6GyDQ4O4tNPP8WXX36J+fn5XVnIqVSKdqhkJod20krF4/Fw9OhR3H///VTEC1iLzcViMXQ6HUpKSuBwODidKSXPIhAIrBOh4/P5WF1dhUajwcrKClpaWqj7KxKJIJfLEQ6HYbVace7cOVy/fh3Ly8ucbn4gOHToEJ566ik0NDTQ/xsfH8fJkydx+fLlvF3Hjg32dl03kjVUqVSora2FWq1et3NFIhGMjY3h/fffx8zMDPx+/664S8Ttud3Ngs/nQywWo7OzE4899hjkcvm6nwmFQigUCqhUKrhcLk4bLPGQNquJRyIReDweeDweKBQK1NXVUXefNAHY7Xb09fVhaGiINhJwHc3NzXjqqafW5VgWFxfx1ltv5dU72LbBEjqhSCSi8ct2DUkoFEKlUuHHP/4x9u7di/vuu4+myYkaQ29vLwYHB6n0aS6NNdejNng8HlpaWvDDH/4QXV1ddAGT7yQMolAoVBDSrrcCSdRNTEygp6cHIpGINvjzeDzMz8/jgw8+wOjoKNWhLhRkisUTd9jj8XDbJSYnhU6nw+rqKk0efdsJRDp3SEKirKwMHR0daGxsRGlp6bre0kgkArfbjUAgUBDc0luBsLfMZjP27dtHky6ZIKQB8iwLHaTbSiAQ0DiWbIZ+vx/T09Pw+Xx5zUfsFCQZSiiywJqxLi4uwuFw5L2zaNsGS27gyJEj8Pv9WF5exszMDHw+300Ni7h8ra2tOHz4MJ588km0tLRAoVCsq62mUim43W4a15CAPk/avjn5XKlUijvvvBPd3d248847aTyXCZZlaV+p3+8v6A0KALRaLbq7u1FRUUFPV+JJWK1WXLhwoSDiVmAtSfjwww9j79691GBZlsVrr72G4eHh2/rsnWiSbdtgSeJFLBajpqYGLS0tqK2tRSAQoMaVmYxhGAZSqRRarZaKeFVWVtLSBkEsFsPq6iquXr2KxcVFXLt2DXa7PS/Sl7l0hYVCIcrLy2E0Gr/R1UKelcfjwdTUFILBYMEbK4/Hg0KhQH19/TpWWjgcxvj4OGw2G5WU4TqEQiE0Gg3uuusummxiWRYulwvXrl27bU7ATkKxbRssMUqBQICGhgYcOHAALpcL4XCYxrNE+T6dTsNkMkGtVtOuHb1e/w1yRCqVQjQahd/vx4ULFzAxMYHr16/D5/MVrMA4cCN8qKqqQmlpKYD1wnHkWblcLlgsFvh8Ps7d63ZPAYFAAI1Gg9bWVuh0Ovp3oVAIly9fxvT0NKcb1Mn9EpJEaWkpHnroIZpj8Xq9sFqtGBgYwMrKSla+azub144MNhAIYHBwEAzDYM+ePWhoaKCyKaT4Ty6C0NdkMhnEYvG67oyVlRWMjo7inXfegc/nQyAQwMzMDC2qb5wOVkggJw3DMFhaWqLMptraWpSWltL+Uo/HgytXruCDDz7YcUNBrkBiUUL2CAQCCIVCm74PoqDR3d2NgwcPwmAw0DEWoVAI8/PzOHXqFBYXF3fhTm4Nkl9pbW3FE088AY1GQz1A0vNLauZvvvkment7s0LgIcSZ7SStduQSx2IxOBwOOJ1OuN1umM1mKn+yGd+XnCqkMSASiVCJEYvFgv/+97/w+Xyc79TYKkgmXaFQQKlUIhAIwOl0QiqV0g2Mx+MhGo1icXERs7OzmJ6e5mRcR+qnJSUl9L2SRCDJmhJyhEajQVtbG+rq6iCTySAUCpFOp7G8vIzFxUWMjo7mtT1yKyD5FaPRiIaGBhw9epQ2mQgEAhrWENGFwcFBfPXVV1lJmO1kPOmOhmGRhnK9Xg+TyYRHH30U7e3tuPfeeyGXy9c1IJMaJqGhffrpp+jt7YXVaqUcTBK7ZfskTedhcNJmYBgGKpUKXV1dMBqNWFxcpBIqdXV1KC8vh8lkAsuyOHfuHObn5zEzM5P1wUmbYTv3yufzYTQa0djYiOPHj1MNp97eXni9XiSTSSoM/swzz6CjowNdXV1QKpVQq9W0nv7CCy/g6tWr6O/vv+0SSDbfKaFNGo1G/PKXv0RzczMOHjxIWz2BGwJ0H374IU6dOoXBwcGseUK3imFvdp87Ik4QlzYYDFJRrUQiQRlLarWa9q5arVYEg0H4fD6MjY3h6tWrmJubw/Ly8nfiNM0EIYMolUqUlJRALBbTzYpM7nY6nfTZhUIh2Gy2XSOFbAVkUTc0NECv11N1ENKoIJPJoFAocODAATQ2NkKv19NOllAoBI/Hg/n5eVitVk69bxK6MQwDrVaLmpoamEwmiMVi2pyfTCbBsiz6+vowODiIqamprPZj7+Sd75jpRPRqI5EIzp07h6GhIToYqrm5GdeuXcPk5CTOnDmDpaUlOByOgun73CkEAgHtTGlubkYikYDb7YbX66UnrN1up2M6gsEgzZpy9bmkUimo1WocOnSIKvQ/9thjSKVSVBSdlOcye5rJvU5NTWFychI2m41T90hcXb1ej8rKStTX16OkpGTdcC5Sb/3973+PxcXFrMffeckSZ4J8UTQaxcrKCs6ePQuVSgWVSkXlSBcWFr4T5YrNQHZpkpxRKBRobm6ms2KsViu8Xi9NoBGCBNGFIiEBV9k+5JQMBoMIBALQ6XTrxMc2tgmm02kEg0HMzc3h3LlzmJqaor3DXDJWYP38W2DNYyCJU4/HA7fbjTNnzmB8fJwmQrONvJ6wmV9K+lwvXbpEdyaujQ7MNkhiiXSpyOVyWr4ipw5pRyMlr3g8Tl0qcuJyOQtO+pCDwSDlBmcq3pN3TORuUqkUAoEAxsfHcfr0aapDzDVkJnvIv4PBIBQKBeRyOZxOJ2ZnZ/G3v/2Nc2WorHTrEFeXKAVwdQFmC6QMYDQaUVJSAp1OB4PBQHslSaacKAOShu5M+mZmLZbLSCaTsFgseP7553HkyBHccccdaG5uRjqdxtjYGKxWK+bm5miDRiwWQzgchtPp5Cz1MLPDiGSyJyYmsLy8DK1Wi3feeQeffPLJrnWI3QpZl4j5X0Lm/ZJG5kgkAolEApZlKRea1JML1etgWRYTExNUrpaEOIS5NDs7S+fDFkrokymmQKbzKZVKKBQKXL9+HdPT05wzVmCHZZ1CQS7LOqS0RZQjiEuY8d1UyzcP1MqclHU2gngOmQwdsvDzZajZfqfknghNlki+7HZe4Wb3WTRY7Pw+idGSEkDms8znSZovg+UCcvFOM1U6uVLJyGodtog1kOb2IgobXDHSrSB/mqFFFFHEbaNosEUUUUC4ZQxbRBFFcAvFE7aIIgoIRYMtoogCQtFgiyiigFA02CKKKCAUDbaIIgoIRYMtoogCwv8B0//+PgtHgM4AAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"CPU times: user 16h 59min 38s, sys: 16min 4s, total: 17h 15min 42s\n",
"Wall time: 2h 26min 4s\n"
]
}
],
"source": [
"%%time\n",
"train(train_dataset, EPOCHS)"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "rfM4YcPVPkNO"
},
"source": [
"마지막 체크포인트를 복구합니다."
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {
"execution": {
"iopub.execute_input": "2020-09-23T06:52:40.806455Z",
"iopub.status.busy": "2020-09-23T06:52:40.805468Z",
"iopub.status.idle": "2020-09-23T06:52:40.879438Z",
"shell.execute_reply": "2020-09-23T06:52:40.879890Z"
},
"id": "XhXsd0srPo8c"
},
"outputs": [
{
"data": {
"text/plain": [
""
]
},
"execution_count": 1,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"checkpoint.restore(tf.train.latest_checkpoint(checkpoint_dir))"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "P4M_vIbUi7c0"
},
"source": [
"## GIF 생성"
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {
"execution": {
"iopub.execute_input": "2020-09-23T06:52:40.884645Z",
"iopub.status.busy": "2020-09-23T06:52:40.883887Z",
"iopub.status.idle": "2020-09-23T06:52:40.886037Z",
"shell.execute_reply": "2020-09-23T06:52:40.886450Z"
},
"id": "WfO5wCdclHGL"
},
"outputs": [],
"source": [
"# 에포크 숫자를 사용하여 하나의 이미지를 보여줍니다.\n",
"def display_image(epoch_no):\n",
" return PIL.Image.open('image_at_epoch_{:04d}.png'.format(epoch_no))"
]
},
{
"cell_type": "code",
"execution_count": 27,
"metadata": {
"execution": {
"iopub.execute_input": "2020-09-23T06:52:40.890366Z",
"iopub.status.busy": "2020-09-23T06:52:40.889586Z",
"iopub.status.idle": "2020-09-23T06:52:40.909049Z",
"shell.execute_reply": "2020-09-23T06:52:40.908439Z"
},
"id": "5x3q9_Oe5q0A"
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAASAAAAEgCAYAAAAUg66AAABt1ElEQVR4nO29eXCkd33n/+r7PtWt+z5HGs19D8Y2vsE4Zh2IQxzAsIaldhM2lVSS2qS2KpWEX7IcmyxbRTAhxMZgSEFig8H4AOyxZzyeSzMjaUYzI41G963uVt93//6Y/X7dmsPWXOpu+XlVqcA9rdbz7ed53s/n+zlVuVwuh4KCgkIBUBf6ABQUFN6/KAKkoKBQMBQBUlBQKBiKACkoKBQMRYAUFBQKhiJACgoKBUMRIAUFhYKhCJCCgkLBUARIQUGhYCgCpKCgUDAUAVJQUCgYigApKCgUDEWAFBQUCoYiQAoKCgVDESAFBYWCoQiQgoJCwVAESEFBoWAoAqSgoFAwFAFSUFAoGIoAKSgoFAxFgBQUFAqGIkAKCgoFQxEgBQWFgqEIkIKCQsFQBEhBQaFgKAKkoKBQMBQBUlBQKBiKACkoKBQMRYAUFBQKhiJACgoKBUMRIAUFhYKhCJCCgkLBUARIQUGhYCgCpKCgUDC0hT6AK6FWq8nlcgX52yqVCpVKhVqtJpvNksvlrvlYVvp+tVq9overVCoA9Ho9Wq0Wk8mETqdDo9EQCoVIpVIkEgl5vKvFSv+WOP5SpVTXqVar0ev12Gw2ysrKsFqtBAIBEokEgUCAZDJJKpVCrVajUqlIJpOrfoxFKUCFEh+4eBFpNBq0Wi2pVOqW3tTX8rkqlQq9Xo/VaqWiogKLxYJer2d8fJxwOMzi4iIAmUzmlhyrQumhVquxWCw0NDTQ3d1NQ0MDw8PDLCws0NvbSzgcJp1Oy4duIShKASoEQniMRqP873Q6XeCjukgul5MXiM1mo7Ozk/Lycux2O6FQiIWFBfbt20cwGCQYDBZUwBWKA7VajcPhoKOjg4cffpiGhgYqKirYuHEjCwsLOJ1OJicnuXDhAplMhmw2W5DjfN8LkNhuqdVqtFotRqORbDZLJpMpOpMawGg0UlNTQ21tLWVlZQDMzMzQ29tLKpUiFAopAqQgBaihoYE777wTr9eL0+kklUqxsLBAJBLBZrORSCSIx+MFe9i+bwVIiE1lZSVlZWXodDqy2Sw+n49gMMji4iLpdLpgT4ZLyWazRCIRhoaGmJubw2KxYDQasVqtwMWtl1qtRqPRXJffSmHtYLVacTgc3HPPPXR0dKDX6+V1odVqKSsr44EHHmD37t0sLCywuLhILBYryLG+LwRIr9djMBhwuVyYTCZMJhN6vR6TyURVVRUulwuAUCiEz+cjk8mQyWSK7ibOZrNEo1FisRg6nQ6tVovVakWn02E0Gsnlcuj1enK5XNFsHxVuLSqVCp1Oh8PhQKfTodfr8Xg8uN1uamtrsdvtBINB0uk0S0tLGAwGadnrdDqsVivhcLhgvkNVrtjuMm5+NKG2tpa2tjY+9rGP0dnZyebNmzEYDGi1WhmJmp2d5fjx43zmM58hGo3e0A28mlET4UDUaDSYzWZsNht+v594PH7LL6pSjQ5dK8W6TpVKhcFgwOPx8MADD1BdXU1tbS3r16/HZrNx9uxZAoEAMzMzBINBotEoDQ0NGI1GMpkM4XCYpaUlGcj4+c9/vqrHD2vcAtLpdJSVlbF161buvfdeNm/eTFVVFXa7XYqPSqUil8tJIUqn0yUVSRLbrfwn4YYNG9DpdLz22mvEYjHFGlpDGI1G3G43mzZtoq2tTYbZOzs7cTgcOJ1O3G43KpWKeDzO3NwcR48eJRwOE4/HGR0dRavVksvlSCQSxGIxGZovBGtagAwGAw0NDdxxxx18/vOfR6fTSaG5lFQqRTKZLMqt10rIZrNym/nwww9TXl5Ob28vc3NzJbumG+XS8HIp+sbE8YsHpdVqpbm5mccff5xHHnkEjUYj3yPWt7S0xNLSEtFolPHxcV5//XUSiYRMKxHvLQbWtABZrVb27t1La2vru4pPMpnk//yf/0NPTw+pVGqVj/LG0Wq1OBwObr/9dj75yU/S3t6OxWLh29/+NvF4nHg8zqFDh+jr6+Ptt98mGAwW+pBvGWq1Gp1Ox+23305jYyO33367dMC++eabDA8Ps2/fvoI98a8VYd2qVCqMRiObNm3iL//yL2lra1smPpf+TjqdJhAIEIvFsFgsZDIZkslk0QiPYE0LkE6no6qqCofD8a6WTzgc5ujRo5w8ebJool7vhUgfcDgcmEwmKioq6OzsZMeOHdjtdvR6PTU1NWSzWZLJpNxyjo2NoVarCQQChV7CTUUIj91ux263s2nTJjo7O3nwwQdlVns6ncZkMnHw4MGSESCBSqXCbDZTXV3N3r170Wq1l4mPEJmlpSV8Pp8UICFUxSY+sMYFKJ1O4/f7iUajZLPZy0Qol8tx+vRpBgYGmJmZIRqNFuhIrx2bzYbT6eQv/uIv6OjooKmpCavVis1mkxdcfnLlhz/8Ye68807uu+8+Tpw4wV/+5V8WJPX+VuFyuejs7ORTn/oU9957L06nE51Oh9lsljfqI488wq5du3juuedIJBIls34RPt+8eTPt7e3LgieCbDbL5OQk586d4+WXX2Z4eJjp6WlCoZDM81EEaJXR6XRUVFRgs9kue1rEYjEWFxfp6+vj8OHDRZ/Ap1Kp0Gq12O12GhoaqK6upqqqivXr11NfX09FRYV0qkejUTKZDGazGY1GI0XIYDDQ3NyM3+8v6qfiShG1Tu3t7dTU1LBt2za6urqorq6+4pbbarVKB67RaOTMmTMFOvJrQ0S71q9fT2Nj4zLfVi6XIx6PMz4+zunTpzl27Bh9fX1MTU0RDodJJpMkEomiDaysaQGyWq3s2LGD+vr6y5yRfr+fw4cP8+yzz/LSSy8V7Y2YXxxrsVhYv349n/nMZ9i+fTvt7e3o9Xp5o4kMbmHN1dTULEtWVKlUUoD0er10upcqWq0Wl8vFE088QVdXF3v37pX5UVfDarXy+OOP88Ybb5SMAGk0Gmw2Gx/72Mdobm5edi1nMhkWFxf52c9+xptvvslLL71UVAm078WaFSBhfouwu0CEHwcHB/nud7/LwMBA0YmPeOKJ/CVhxZhMJmpra3G5XOj1eunXgIuO9KGhIU6ePElPTw/z8/PYbDY2bNjA5z73OVlJD1BWVsbv/u7vcuLECQ4dOlTIpV4Xra2tbNiwgY0bN1JdXc3OnTtlNrtKpSKTyRCLxchkMiQSCUwmEzabDbh4XXR3dzMxMSF9Q8VObW0tTU1NeDweLBYLuVxOPmx6eno4e/YsL7zwAmNjYyUlPrCGBUiv12M0GikrK8NiscjXhQCNj4/zy1/+suhOlsjnsdlsNDU1sWfPHjQajSyzsNls6HQ66TwXEZ5YLMbAwAAvv/wy+/fvZ2pqCoAPf/jDPProo7LWDcDhcHDfffeRTCY5ceLEsvBsMSOEuampibvuuov777+fhoYGuS4hPplMhmAwSCKRIBKJyFYUYhvb2NhITU0NBoOh6K1AlUpFZWUlzc3NMuCQy+XIZDLE43H6+/vp6enh4MGDpRnBLfQB3ArUajVtbW10dHRc5gvIZDKMjo4yOztbdJaPWq2msrKSpqYmvvjFL+J0OrHZbFy4cIHp6Wn+4z/+Q7ZQ0Gq1aLVaNBoNcFFYg8Egfr+fUCgkb6qJiQmee+459u7dS3d3NwB2u5277rqL2tpadu/ezZNPPklvb+81JSwWIru5traWP/zDP6S7u5tt27bJhFIhPOl0moWFBebn53nyySfx+XzU1tZy22238eCDD8prQa1WU19fz+/93u9x8OBBTp8+veprWQmiXvGRRx7hgx/8IC6XC61WSzqdZmxsjPHxcZ566inOnTtXssmma1aA6urqqK2tvSxXIpvNEgwGiUQiBRegfEeisHDq6+tZt24dGzZskAWofr+fqakpJicnlx17fo6I+JxL+xcFg0F6e3tpb2+XkUCNRoPT6aSxsRG1Ws22bdtQq9VMTk4Si8UIh8PLLCLhrL7S31wtRAbwxo0baWlpwev1ks1mSaVSTE5OEo1GZWuS+fl5+vr6ZA1UZ2cnmUxmmW/I4XCwceNGhoeHGR4eJpFIFPx6uBSXy0VNTQ0tLS00NDRgMBiAi9HdqakpTp06xdjYGPPz8wU+0utnTQqQVqvlvvvuY+vWrdJCEGQyGWZnZ/H7/QU6ussRWwOz2cznPvc5NmzYQENDA4ODg/T39/Pss8/S399/XTfJ2NgYzzzzDO3t7Wzfvh2z2SwtQq/Xi8fj4Rvf+AY+n49//Md/ZGBggIMHD5JMJqWlBcitTX4HvdVCrVbT2NhIV1cXO3bskFvqWCzG/Pw8f/M3f8PQ0BBnzpyRPpBkMonZbMbhcLC0tLQsF0qlUlFbW8ujjz7KzMwMk5OTjI6OFl1u0J49e3jiiSfYtm0b5eXlskdVIpHg5Zdf5oc//CGzs7OFPswbYs0JkEajwWAwUF5ejsfjuSz6BRdLNEwmExaLhUQiURTmqzg2Ubmv1Wrx+Xz09vbi8/muO4tVOGRPnDjBiy++yN13343L5ZI3ovCrOJ1Obr/9dlpbW2lra2NsbIzp6WlGR0eJRCLLylSy2eyqCZDL5cLhcHDvvffS1dWFSqVifn6excVFjh07xsjICH19fczPz8tmbOInHo8zOzvL+Pg4g4ODtLS04HQ6gYuiZjKZqKyspLGxkZmZmaISIK1Wi9vtpq2tDZvNtqx9r7her5SMWGqsOQHS6XTywhJPDUE2myWbzWI2m2XPlKWlpcuckKtliuf/nfwbW2yTZmdnOXz4MIuLi9ftJM7lcqRSKQ4cOMDMzAzd3d3SkZ1fZ2Q2m3nwwQdJJpOEQiFef/11jh07xs9//nMp0tfbI/tGKC8vp7m5md/5nd+hsbFR+j9OnDjBP//zP9PX13dVJ3I8HpfJecePH8fj8eBwOICLAmQwGKiqqqK9vZ0TJ04UTYmKyG/yer2sW7dOvi6++3Q6jdFoxOFwyGBDqbLmBGj79u1s3bqVqqoq2V5VhCynpqbw+XyMj49TV1fHk08+ueyJGYvFGB4e5ujRo7z++uuEw+FViyyIkPGxY8dIpVJUVVURDAYJBAI35RgmJycJBAJ86UtfwuVy4fF4+MAHPsBDDz2E2WyWT1MRgduyZQvl5eUcPHiQhYWFghRyqtVq7rjjDj760Y9SX19POBzmqaee4syZM5w8eZKxsbF3jWBls1kSiQTnzp3j+eefl5Ekq9VKOp0mFApx9uxZjh49SiQSWcWVvTuVlZU88cQTfOADH1j2ujg/LpeLBx54gIaGBv7qr/6KkZGRwhzoTWBNCZBwPm/evFlGSIQpHo1GGRsbY25ujtnZWdmqUmx3crkckUiE/v5+stksFy5ckKFccfOJWhtROS+E7WYgPn98fBy32y3/jph2caNEIhEikQivv/46BoOByspKWdxYU1MjrSLx9K2oqJBb1UJMKRFpA+J8ij5Hx44d48yZMytOIsxmswQCAcbGxggGgzLlQFh6CwsLTE1NFU0IW61WY7fb2bt3L83NzZf9u0jJaG5uxmw24/F4mJ2dLVhHwxtlzQiQeHLv2LGD3/qt35IFqMlkkr6+Pt544w1+9atfMTExgd1uZ8eOHWzdulX2ylWpVFitVrZt20Z3dzdf+MIX5JYtmUwSjUaZn5/n6NGjnDp1iuPHj7OwsMDk5ORNuzmz2SynT59Gq9VKp68QupuF8AmNjY3x3e9+l3//93/nr//6r/ngBz8oc2rElgyQAr3aGAwGvF4vXq8Xl8uFRqOReUs+n++aPstms1FXV4fb7cZisci+yMeOHWNoaIiZmZmiESCHw0FNTQ07d+6UGeyXolKpcLvdmM1mHnroIWpra3nhhReKOp/paqwZATKZTFRXV8vEQ1ETdfbsWU6cOMGxY8cYHh7G5/PJ119++WWcTidWqxWNRoPdbmfLli0YDAaZOQsXK+bj8Th2u51kMonFYmFwcPCab4T3IpfLEY1GZUdGi8VCfX09yWTyphVOCr9POp2WTarm5+fx+XzU1dUte5/4Tux2+6rXjVksFlpaWnC73eh0OuBiKL6lpQW1Wr0if02+n2fTpk04HA7ZL2dqaorjx48zOztbNIWaGo2GjRs3snHjRtliV1ju0WiU6upqzGYzdrtdWqobN27EZDIRjUYZHh5maGio0Mu4JtaMALlcLnbs2EFVVZW8YOfn53nmmWc4evQoBw4ckO/1+XyMjIzwyiuvyBvSbDbT3d3Nt7/9benAFuh0OmlhVVdXs2fPHn7+85/fkuhZLBaTUafq6mruvvtuAoHADbfPEBGvS4Ukm80yPT3NyMgI69evR6/Xy/eLhL2FhQUGBgZu6O9fK+Xl5dxzzz00NjbKgQEej4dPfOIT/OpXv2JkZOQ9LUPRgH3Xrl08/vjjeDwe0uk0k5OTHDt2jGeeeYalpaWiyAIXc98+85nPsHnzZjQaDdFolEAgwL/9278xOjrKI488QkNDAxs2bAAuru9jH/sYsViMj370ozz99NP8r//1vwq8kmtjzQhQZWUlv/VbvyX3zdPT0wwNDS0rS7gS4mZMJBKMjIzw93//91gsFiwWC0888YTMHhakUilisRh+v5+lpaWb+uQU/qpUKoXVaqWtrQ2j0cj+/fsZGRm5IcFzu93YbDZpXSUSCfR6PWazmba2NtatW3fZVkvky8zNzaHRaFbNxFepVLhcLpn/Il6zWCzSH9TW1sarr77K6OiozPwWHQDMZrMMRGzdupW2tjasVqu8oZ966inOnj0r84OKAdFK9fz58ywsLPDMM89I3+XAwADBYJD5+Xm8Xi/Nzc3cf//97NixA7iYulFZWYnH45HnuFS2Y2tGgNxuN3v37sVqtZLL5Zibm2N0dFQm8L0X6XSa2dlZfvjDH8rtxz333HOZAMXjcZaWlmRG8s1GJAAKU9vj8VBeXo7ZbL4sQ/lK5Fs64r2icVl5ebmMqkWjUSwWi5wdVV9fv0yAxA3tcrlwuVxXtJ5uJWILJsLm2WwWnU5HY2MjXq+Xrq4upqenicViMjSdf7x79+6lo6ODe+65B3jn/I6NjfHSSy8xOztLPB4viq0XIMcnj42NEYvFeOmlly6b13XmzBmsVis1NTVUVVXR2dkpgwQulwun04ndbieVSikCtJqI8KTZbEan05FOp/n2t78tQ9rXisjJSafTy7KBAZ555hn+4z/+g9HR0Zu5BIkoHUkkEjJB8IknnmDXrl38wz/8A36//4pPbVEtb7VaaWxsxGQySYe21+ulqqoKj8cj27WKaQoiD8ZkMknRymQyDA4OMjw8zDPPPMP58+dX/YIOBoMMDAzQ3t6OWq2mv78fn8/H/Py8PNcPPvgg999/PzMzM3IEsd1ux2KxUFZWJluRnDp1irfffpsXXniBwcFBpqamisbvI6J9wvr99a9/TSwWk030LiUajTIyMsLf/u3f8p3vfIe//du/pb29Ha/XS2trK4899hj/8R//UTK+oDUhQFqtVvpp1Go1iUSC0dFRxsfHr/siu9rviRqcWxX2FEmI4uLTarW0tLSg1WrZunWrFCDx7/lWjsVikQ3LDAaDvLgrKirk07G5uVk6lt1ut2zYJqrqo9Go9PmcPn2aCxcuMDMzs+p+kmQyyczMDDabjVwuR39/v6zzMhqNWCwWKioqMJlMOJ1OKioq2LRpExaLZVnqQDQalZNjBwYGiiZnRpTfCDHVaDQkEgl8Ph/xePyqvydym0ZGRpienqanp4dMJiPPfWdnJ5WVlczPzxMKhYrCv/VulLwAqdVqWTUueuRkMhkWFhZkAt31otFoLvOLhMNh5ufnb9nTU1S4548Ham1tpaWlhdtuu01WfYsfMXZHbNusVqvcPgUCAVlqIXxL4r+rq6vR6/XLMqLT6TQjIyP85Cc/4dVXX5UWZCEuYp/PR09PD0NDQ+j1en784x8zMzMjhV+lUmGz2eQE0O3bt3P33Xcva1caj8eZmJjgzTff5F/+5V+KouQG3okwer1e7HY7NTU1TE5Oymm8KyWRSPDXf/3XdHd38+STT+Jyubj//vsZHR3F4XDIsUzFYOldjTUhQCKXR3ClqvBrQfheRC4MvJOpnEqlbukJTSaTzM3N8fOf/5xNmzaxfft22UxMWClCZEVZiSgSFZMxxdpFTo9Wq5WJjdlsVj558zsFxGIxfv3rX3PmzBneeustxsfHC1YblcvlCIVC9PX1YTQa0Wq1cnyw+P5VKhXhcJhcLsfk5CRNTU3LPkNYUD/4wQ84fPhwUeT5iMhiXV0dHo+HHTt2SOttcHCQsbEx3nzzzWuKeIq2LAaDQTrg9+zZQ1VVFfX19czMzDAwMCDbtIjE1mIRpZIXII1GI/N/bla5gMfjobu7e1knRZG6f6sv5EQiweTkJE8//TSPPPIIXV1dsiNifntWYZmZTCZplgtxElaAyIcS/XJE+wpYXsgoGnh9//vf5+zZs5w8efKWrnEl+Hw+Dh8+LItmL03IFD6TbDbL2NiY7O+UX1Zz4cIF/uEf/qFohg2I87Z+/Xo6Ozt57LHHcLlc2O12Tp48ycDAgGwjshKrU2RNu1wuGbm1WCzcc889pNNp5ubmZDeFgYEBxsfH5cNKEaCbRDqdZmhoiLa2NuAd81b0uDl+/LhU/Py+OVfCYrGwYcMGPvShD/Gxj31MfiZAb28vX/va1+jp6bml68lms8RiMYaGhnj22Wc5cuQIjz/+OBs2bKC2tvaKFdDCysn/byFUgnwRg3du4GQyyb59+xgYGODw4cM3PbnyehGRrfzo26WdDcQ46jvvvJMtW7ZIsUqlUjz55JP09PQUVZ8fj8dDQ0MDDz/8MJs3b6a+vl52P+ju7pbDBoaGhnjqqacIBoOyp1F+2Y9arWbDhg20tbVx11130dDQgNvtRq/Xy+9IVNN3dXXJxmt9fX2cPHlS5pUVg3+o5AUom83i9/sJBoNkMhkpQC0tLTLLV7SRyL+Yr3RROhwO1q9fz+bNm9m5cydw8UIPh8OMjo7ym9/8hnA4fMvXJIbKRSIRRkZG2LJlCyaTCUA62kXz9fwiUtHtD1gWhs+veler1TILOhwOEwgEOHHiBH19fUVXU5TfAA2WpxgIX5bdbqe1tZWampplvqzjx49z/PjxogpHi6ZqTU1NMjdJnLOysjLcbjdlZWXU19dz6NAhFhYW8Pl80h8o/ENqtZquri42bdrEbbfdRnl5OQaD4bLvSURRW1tbmZqawu/3c+HCBTk7rBimopS8AAmB8Pl8zMzM4HA4MJvNfOELX5DO2ZUiTpqoooeLTufvfve7HDlyBJ/Pt6pPjVQqRTqd5mtf+5r0A4n9fnt7u2zSJRLuLBaL9FsJC0ek7IsiRpEP8+Mf/5je3l65rlgs9q7Rl0IhbioRELDZbBiNRsxmM83NzdTW1rJr1y6qqqpkw654PM7w8DAjIyMFv8HySSQSclig2ApfKho2m43u7m6+9a1vyVpEsYb8/xUBBCE8yWRymZUrep8Hg0EmJiZIp9NYrVaqqqoAWFhYKIp8oZIXIHjHCjp27Bjt7e3U1tbK+q4baR8qGr+fPHmSoaGhgpisotezQFg/KpWKUChEJBLB7XYzPz8vfQDiwhUCZDab8Xq9OBwOMpkM09PT9Pb2ypyYYp4bJSyg/Lqu8vJyamtrqauro7y8nLKyMsxms/T9LC0tyahfMRGPx/H7/YyOjlJeXk5XV5d0sucLkU6nw+12X/Vz8kVVWEZiO53fpUFMSB0eHmZmZoZQKLTMkV8MrAkByuVyDA8P80//9E984hOf4M4776Surk7WhF0v4XCYmZkZXnzxxaJpfSkczkNDQ7LURPiARCREdC9MJpPo9XrZ3mH9+vXkcjlmZmZ46aWXiEajRdUF8N1Qq9WyT9H27du54447sFqtGI1G2eExm83Kfk/FlOUsCAaDRKNRfvOb3zA/P095ebkskRGs5GGZ/x5RVuP3+5mdnWViYkJasyMjIwSDQaampqTzeXp6Wror8r+fQnVWXBMCBBAKhRgYGODZZ5/ljTfewG63U1lZycc//nHKysoua88qEE+L6elpfD4f/f39zM7OykbnouyimMlv0ylygER/IWENHT9+nPHxcYBlFfelgOjqGA6HOX/+PBUVFSwsLGA0GlGpVLJkIRQK8fLLL8smasWGOE8nT56UfaiNRqO0aIX/0ul0ylB6Y2OjTCoVgpHNZllcXGRxcZFDhw4xPz/PxMQEoVCIQCAgO1iKWjcxxCCbzcrXiiUUv2YEKBaLMT4+Lm8yMZpn48aNNDU1yezYS0mn0ySTSUZHRxkdHeXFF1+UzeBvdi+eW4m4SS/ddojQu/CJCP9AqYiPQPQxmpiYYHp6mvn5eVwuFwaDQSZkzszMcPDgQX7xi1+wtLRU6EO+DOFUF5M4jhw5Iv9NCJBWq6WqqopcLseGDRuw2WxYLBbZEUAIycTEBOPj47z88suMjo4yMjIit2DCt3Mlgbma6BRKjFS5YpDBS7hZ5qCYLmowGGSbiSshfAfJZJJgMEg8Hr+hDNKV/t5qm71XatB/I6z2OoV/RFSOb968mYqKCtxuNz6fj1OnTjE0NMTk5ORNrfVazXWKNZaVlWEymWSZxqURq0QiQTKZlKU5+Z07rzcfrhBSsKYFqFAUqwDdbAq1To1Gg06no729nbKyMsrKyggEApw7dw6/3y8zpG8Wyvm8dSgCdAtQLtjl3Kp1ihwakYQp/Hk3O6JX6HWuFoWQgjXjA1J4/5HvE3mvLHeF4kQRIIWSJt/fUeoWyPsRRYAU1gyK9VN6XB6XVlBQUFglitIJraCg8P5AsYAUFBQKhiJACgoKBUMRIAUFhYKhCJCCgkLBUARIQUGhYCgCpKCgUDAUAVJQUCgYigApKCgUjKIsxRCNw252juSVxtlcOnmhFPvkrDb5s8ZWwo2ez0JNbxDnZ6VN6Ur1fAqUavj/RyG+CCUh/Nq41u/rer7fQt/Ql84iU7j5vK+3YDdrkmopcTNuqFstPpfO/yok77frY7UpSgvoVpF/Qb9fxcdoNMqZUcW4ftGSVHQ9FK1HFdYm7zsBunS6wPsFsXa9Xk8ul5M3dTGJkHhAiKF7er1ejhdSWJu8rwRIjKiB4rrxVgPROTB/fPWlkzev9fNuNmq1GqPRyLZt2wBYWlqS45EU1ibvKwF6v4nOlRDtS/Pny1utVrRaLZFIhFQqRTQaXSbWq4mY5CoiZ/Pz86t+DMVA/qTUfC4d01zqvK8E6P2O8P2I+VNer5e6ujruuOMOPB4Px48fZ3Jykr6+PsLh8A2NJroestmsHDNst9tpbGxkdnZ2zdxsK0VYqGq1Go1GI18Xfkthya4FF8KaFiBxowmHpsgnEZMi3w8Xdv7UiPycp1wuh81mo7GxkXXr1lFTU0N5eTlLS0vs3LmTQCCA3+9n//79+Hy+VdkGiWmuPp+PVCqFWq0mlUpddx6QRqPBZDLJNc7NzbG0tMTAwEBRzUcHpDUqrlkxdtpsNmM0GlGr1fIcqNVqOX4oFovJsculyJoVIPH0MBgMcsCbSqWSs9XFE6SYLsKbidhmabVaTCaT3FKJGy+Xy+FwOGhtbaW7u5vW1lZMJhNw0RKZmZlhamqK6elpUqnUqllDmUyGubk5YrEYAPF4/LoESKPRoNfrcblc7N27l8cee4yenh6Gh4cZHR0lFArd9PE9N4K4TsU1W1FRgdPplHPPdDqd3I7qdDpGRkaYmppicXFRXs+l+FBdcwLk9Xrxer189rOfpaamBpPJhFarRafTEY1GSSQSLC0tMTExwcGDBxkdHWVmZkb6PUodlUrFI488QmdnJ93d3XIirN/vx+fz8fTTTzM1NUUkEmF0dJSXXnoJm83G/Pw8O3fulN9XWVkZRqORj3/845w8eZKnn356VZ6y2WyWYDBIMpkkk8kQiURW9HvCcti2bRudnZ1s2bIFl8tFeXk5FRUV1NbWUltbSyQS4Y477uDgwYN8/etfv8WrWflxV1RUUFFRgd1ux+FwsH79esrKyigvL8fhcKDX68lms/LBGgqFiEQijIyMsLS0xPj4OHNzc0xNTTE5OUkoFCKRSBR6ee/JmhEgnU6HzWajrq6OhoYG7rrrLpqbmzEajdIaCAQCcuzyhQsXiEQi0vT1+XzE43FCoVDJPUUEJpMJm83G5s2b2bVrF7t370an05FOp+WF+dxzz0m/SiAQIJlMMjAwgEajoaGhAZfLhdvtRq/Xo1arqa6uZnZ2VjqFbzX5OUpqtZpkMrmi82EwGHA6nXR0dLBz507p1yorK5Ph/bKyMnK5HI2NjaTTaaxWK4lEoqDbF+HvsVqtUnDKyspoa2vD4/Hg9XqxWq3o9Xp5TlQqFalUilQqhdfrZWlpiYqKCiYnJ7Hb7cBF5/3MzEzRP1TXjACtX7+eL37xi2zatImWlhYcDof0fSQSCSKRCEtLS6RSKVwuF1u3bmX79u3EYjESiQT79+/n1KlTfPOb3yQej6+KeX6zh+nde++9fP7zn2fjxo14vV4MBoP0+fj9fkZHRwkGg8RiMXkBR6NRfvSjH2GxWPj1r3/Nzp07+eIXv4hGoyGZTPLTn/6UkydPrupNmslk5HlZyTZZp9PR1dXF448/zrZt22hra5ORvUuzqVUqFVarlba2Nj7xiU9w8OBBzpw5c6uXdFXENtliseByuVi3bh1er5f6+npMJpN8gGYymWUWjd/vJxQKYTabcbvd7N69W25VDx06xJkzZ/jyl7/M0tJSwda2EkpagISTcdu2bWzcuJH169dTX19PWVkZqVSKhYUFDh06RCwWIx6PEw6HyWQy2O12+ZRxu9243W46OztRq9Vs2bKF8fFxRkdHV2UNN0N81Go1VquVqqoq2tracDgcAPT19bG0tMT8/Dznz59nbGyMpaUl0un0snBuJBIhmUwyNjaGx+Ph3LlzJBIJwuEwo6OjLCwsrKpVKP7Wez0EhPXg9Xqpra2lo6ODyspKbDabvBkzmYwc4Zz/e+KmHRkZKbgACZ9Pa2ur9PeMjo5K53L+dy+iYMIBbbVaKS8vp76+HqPRiFarpampiXQ6LR/AxUzxH+FVUKlUmEwmqqur+f/+v/+PxsZGqqurgYsnKRQKceLECT71qU8RiURIp9Py99RqNd3d3Xz605/mQx/6EJs2bWLbtm00Njai0Wh48cUXV0WAbtZNbTAYqKuro7m5mY6ODpLJJIuLi3znO9/h1KlTHDx4kFQqdVVrIpfLkU6nmZiYQKfT8cILL0jfWG9vL8FgsCi3pSqVCoPBwPr169m8eTNbt27FbDaj0+mkDwmQWdX5llB9fT2f/vSnOXHiBK+99lqhloBWq8Vms7FlyxY+/OEPEwwGmZ2d5YUXXmBycpKxsTFCoZBcT34gQaVS4XA42LRpE3fffTdGoxGNRsO6deuwWq3odLqCrWullJwAqdVqamtraWlpYceOHTQ1NdHY2IjdbieXyzE5Ocn09DT//u//zpkzZ2SYUiCeIBMTEzz33HN4vV4aGxux2WxYrVY2btzIiRMnCrfAa0SlUlFVVcV//+//nY0bN5JOp/n+97/P8ePHefPNN1lYWHhX8RFPYBExSqfTHDt2jLm5Ofx+f1E653U6HQaDge3bt9PY2Mjdd99NQ0MDZrMZjUZDKpWir6+Pubk5zp49S2dnJzt37sRut0unvLCejEYjVqu1YOu0Wq20t7fT0NBAeXk5vb29nDt3juPHjxMMBgmFQqRSqWVRLnEuVSoV0WiUUCjE7OysFORiKOJdKSUlQKKWqbq6mm3btvHwww/T3t6O0+kELoZsx8fHOX36ND/60Y+uasXkcjkWFxfZv38/9957L+FwWOZdNDY24vF4VnFVN4awAj/+8Y9jMplIp9O8+uqrvPzyywQCgXe1XER+lM1mw2Qy4Xa7SSaTnD17lqWlJSKRiLzwiwWtVovZbMbhcLBt2zY2bdrEfffdJ89fOp0mlUpx7tw5BgcHef3114lGo6xbtw6j0SgFCN4pzrVYLMTj8YIIkNlsprGxkcrKSpxOJxMTE5w7d46hoSFptV+NXC4nXQuBQEBuvQWlIEIlI0BarRan08ltt93G5s2b2bNnD9XV1Wg0GhYWFjh9+jTf//73GRwcZHx8nOnp6RV9roh8eb1edDqdNOGLHXHzfPOb32TLli3YbDai0Sh+vx+/3/+u2ybx9O/u7mbXrl1s3LgRm81Gb28vFy5ckLk/xSY+FouFdevWcc899/CJT3wCr9eLxWLBbrejVqvJZrOEQiF8Ph8/+9nPGBwclDdofg1gfpmD1WrF6/USDAbf84a/FVRXV/Pbv/3bNDQ0EIlEePvtt+nr61txEESE8W02GwaDYdm/FdO5uxolIUAihFpVVSWzds1mM4uLi/h8Pubm5ujv7+f48eNMTEywsLCw4s9Op9PLWlOUivkqclw2bNhAR0cHGo2GxcVFTp06hd/vv+oFbDabMZvNVFdXs2HDBjZv3kxXVxdms5mJiQkpPsWSpCl8dk6nE4/Hw5YtW9i8eTMbNmyQUS4hPGNjYywuLjI/P8+FCxdYWFjA6XSi1+vRarWXpRJks1k0Go38nEIgat8ymQzhcBi/3/+elms+Wq0WvV6PwWCQTudMJlNUSZbvRlEK0KVhU71ezwMPPEBHRwd33303oVBIJhJeuHCBgwcPEo1Gr8uMjsViBINBecKK5cZ7Lz70oQ9x1113UVdXJ598r7/+Ol/+8pevav0JB2VHRwd/9Ed/hMfjkdvNcDiMyWRCrVbLotRCkd+MTNxg9913Hxs3buSLX/wiZrNZbqVyuRyxWIyDBw/yP//n/2R2dha/3086ncbpdLJ+/XoaGxtxu93SshV+FGHlidcKQTgc5syZM3i9XoxGIz6f75qSL+12Oy6XC6fTKTPZhV+o2Hx3V6JoBUiIkMlkwmKxUFFRQXl5OXq9Hr/fT29vL2fOnJFZn+Kpfa04nU5qamrQ6XSkUikWFxcJhUI3e0k3DXFT1tfXs2XLFkwmk3x6BgIBWUclMJlMlJWVsWHDBlpaWmhoaKCyspLq6mrMZjNarVZagadOnWJ4eHhZmL5QmEwmPB4P3d3dtLS0sG3bNurq6rBYLPJJ7/P58Pl8vPjii/T398trQZRxZDIZua261MoRuUahUIhAIFAwiyGdThMMBmV3gpX2PhL+u87OTtatWydrHYU16Pf7C34OV0JRCpDI9hR7dLfbTXV1NV6vF7VazfT0NG+99RZnz57F5/PdUMMqr9dLc3MzarWacDjM5OQkgUDg5i3mJiOiVu3t7TL5LJFIsLCwIJPTxM2Un3T36U9/mo9+9KMYDAa5FRHNvtLptPQ/TExMFIX5brFYaGtr49FHH+X+++/H6XQuKyjOZrNMTU0xODjI3/zN37C4uHjZDSeENT8XSPx+Op2WW56FhYWC+H8AUqkUgUCARCKBWq1e0XcvHkImk4nt27ezYcOGZQLk9/uZn58vivP4XhSlAOVbMoFAgFgsxrPPPovFYsFoNDI/P8/ExMSyrdO1Ip44okOiCOH/xV/8BefPn79ZS7npiG1FeXm5vJkmJyf5+7//e/r6+sjlctIp+alPfYqWlha2bNlCY2OjrKqGd5qzicJTkW8Sj8cLvMKL1NXV8dhjj7F582aZ1S4KiV966SW+//3vEwgECIVCV3W4R6NRent72bx5M+l0ellwYXJykp/+9KcMDAwULAIGyGjs/fffz8aNG6mvryeVSuHz+aQ7wG63YzQaZZ1YTU0NVqsVq9XKfffdR21tLSqVSuYKPfvssxw4cIBwOFyQNV0LRSlA+ReT6Ak8MDAgnxD5P6Jm6Forgc1ms8yaBWTy3oEDB4q6A5/FYpGlJvBOJnNPTw9zc3Po9XqZHbtnzx7a29vZtGnTsu1Hfha0yKpdWloikUgUzBLIR/g2NmzYQEVFhSwpSSQSTExM0NPTw89//vP33CqmUinm5+fljZi/7qWlJZkrVEhLIR6PMz09jVqtpry8nMbGRjKZDBaLRR6X0+nEarXKOr2mpiaZt9bc3Izb7UalUslyo97eXnp6ekqiRUfRC5D47yupeX7LDVErsxIhMhqN3Hnnnfzf//t/KSsrA6C/v5/+/v6i8H+8G83Nzfy3//bfqKurA96J5JSXl0tR/a3f+i26urr4wAc+gNVqlV0QgWXbM5FZK/xH+dnDhUIk05WVldHR0YHRaAQuHveZM2f4vd/7Pebn51d8c4nzKaxd8VmLi4scPXqUubm5gp5vkQxpsVgoKyvjK1/5ikwpEOcsP3qXTCZZWlqSuwGRfKnT6Thy5Ag/+tGP6OvrW/VmctdLUQrQlbjal6nT6WhtbZWNzOfn52UzLXHxCX+S0+nEZrOxadMm9u7dS3V1tTTtp6enS6N6+P81q8pPqLNYLOzYsUP6OzZu3EhjY+Nl7xPkWwLJZJKJiQnpfC40whJwu90yqzedTtPX18fx48eZmppasYWq0+moqqrC5XJJ/4/wkfh8Pvx+f8G3nMIfBcg2KMKfc6nVmslkZH8kk8kk/XnZbJZAIMDU1BRnz54lHA6XhPhACQnQ1TAajTz44IPU1NTQ0NDAm2++yfHjxzly5AjBYFD2UNFqtbS3t7Nu3Tq+/OUvU1ZWJm/OdDrN6dOnOX36dNGfuPxUfLh4w1ZWVvIHf/AHMqdFFCVeujW9dG3JZJJwOMxbb73F22+/XRRPTb1eLyN2wscVj8d56qmn6OnpkdnZK8FqtbJnzx5aWlqk/yeZTMpM45mZmYKvN51Oy8CBOGdXan0ivgvh3xO5TQCRSITz58/T39/P0aNHV3sJN0RJC1A2myUej8v97oYNG1i/fj0OhwO32008HqesrAyv10t1dTXl5eW4XC7sdvuyNqXpdJrz589z/vz5gl+Q74Ver5fNwuCdiIgwxcWPeOJfihCkVColG7PNzMywsLBQFNaf2B5v3LgRtVrN+fPnGRkZ4eTJkwwPD6/4GNVqNV6vl49//ON0dHQA72zln3rqKU6dOlUU51pEIA8fPoxKpWLHjh243W48Ho88j+FwmFQqJRvrifQJjUZDLpdjYWGBb3/72/T19RV6OddMSQuQ2EKcO3cOp9OJVqulsrISq9WKRqNBpVLR1tZGc3OzbLcBSMtA5InEYjHGx8eZmpoqiovy3RD1cKJZucgUNplM8v/nc2nPISG4iUSCQCDAxMQEi4uL0losJML/s3nzZmkBTU5Ocvz4cYaGhpiamlrxZ5nNZrxeL3fccceyQIPf7+eXv/zlikt1bjUiH6m/v59IJILJZKKmpoZMJiOtnIWFBeLxuCw7sdvtUpzE9usXv/gFwWCw0Mu5ZkpagADZRsLv93Py5ElpxhqNRlpbW3nkkUdwu91SkMQNGIlEmJ2d5e2336a3t5eBgQHZvEncxMXYY7e3t5cvfelL/N7v/R533323fF2sTUQFBflCm06n8fl8zM/P8+abbzI4OEhfXx9nz54lGo0WfK0GgwGr1Up9fT0ej4dMJsPrr7/OM888s+LxPKK04ctf/jKbN2/GZrPJCvmvfvWrvPnmm/h8voKvVSAE6Ny5c4yMjNDT0yOr/cXDQ7gRqqqq+MAHPsBf/MVfyN8X7xFN5kqNkhcguBiqF0900brS5XLh9Xqx2Wyyq5wgmUzi8/kYGBigr6+P3t5emU1d7CwtLXHy5Ek2bdpETU0NZWVlGAwGDAaDbC+bb+2I6GA8HicejzM0NMTk5CS9vb2MjIxw4cKFZcWahcRiseBwOKSDNZfL4ff7mZiYWPG58Xg8VFZWsmHDBtrb29FqtTLj+fTp0/T39xfdpNVsNks0GiUajV4xCVZss0OhEE1NTcsc1PkjeopFVK+FNSFAAuETEtGgpaWly1owiKkLhw8f5n//7//N9PS07AddCidR3Ejf+ta3+MUvfsGjjz5KY2MjbW1t2O12nE6nFJN0Ok00GmVhYYH5+XkWFhb413/9V4aHh7lw4YJsy1osa25tbaWrq0vWpImOgNciGPfffz8PPPAA3d3duN1u1Go1IyMjHDp0iIGBAaanp4tmvStFPEhEO938h6kQrlJbk2BNCVA+DocDh8NxmeUTDAZ54YUX6OvrWzY9oBTEB5bPzkqn0/zmN7+hqalJ9gUSTcnhomUYCoWYnJykv7+foaEhzp8/z/z8fFGu2e12U1lZKcdGX0+Gsl6vl/Vi+Zni+/fvv2K5Rqmg0WioqqrC7XbL1zKZDCdPnqSvr68oLNjrYU0KkEqlwuv1ykiCEKFEIsH8/Dz/8i//wsTERFH5Aq6FXC4nCzGnp6dpamqivb0dvV5PTU2NdLLH43H8fj8XLlzgjTfe4O2332Z+fr7otiCCyspK6uvrZYGs6FV9LYjq+fy8nwsXLvDLX/6yqGv83gvR67m6unpZUulbb71FT09PwRNIr5c1J0AiTPnJT36STZs2yVBlLpdj3759nDhxgunp6ZIev5NPKpVicnKSJ598kt/5nd9hy5YtUnTtdrucarq0tCSTM4uVQCAgW8jqdDosFssVEymvhkqlkn2OxDDGZDIp118KPr5LUalUuFwuKisr+f3f/33a29vlv2UyGfbv38/x48dL1gJanWFPq4jVaqWiooL169ezbt06ADl+ZnBwkP7+fsLhcNFaAdeKKKXo7e1lfHxcrkuE60WN0PX2S1pNREmIEAq9Xo/T6aS8vFxmB18NMSHF5XLh8XhkhrtYu9hylgqi64Hdbqe6upqmpia6u7tpbGyU2eEifWRycrJkH6ZrygJSqVR89KMf5YEHHqCrq0u2KZ2ammJ4eJiXX36Znp6egqff32zEdmtiYoIjR46wceNGPB4ParVaTgeZm5sr+huwr69PVreLmej/+T//Z+666y7+5E/+hKGhoWXdK/MpLy9n586dNDY2SrEKh8Ps37+/aBNML228J9BoNNjtdjo7O9mxYwf33nsvzc3N1NTUyOjghQsXGB4eLqmyiyuxZgRIpVKh0+nweDxyRlIqlZI9Y06cOMHk5GTJn7B3I5vNXlZMG41GGR8fL4nWDNFolGAwSCQSIZFIyGZqarWae++9l87OTuLxuMxpEqUjdrtdWr01NTXLfH4TExNFNZxP9OPWarV4vV75/9PpNJlMBoPBgMViobm5mfb2djZu3EhTU9NlXQGGhoY4fPjwirsnFitrRoBEOUJFRYV0ZC4tLXHgwAHefvttXn31VRluX6uIHkf5T9NAIMCxY8dKwv8RiUTw+/3Mzc1hs9lwu92y3ehXvvKVZT6dUCjE1NSULMERU0SF/yuTyRCNRjl9+vQ1ZVDfSkSdlxihfdttt8mJJEtLS0SjUdmt8qGHHpJDM0Xej1qtJh6PEwgEeOWVV/jhD3+Iz+cr9LJuiDUjQMIHIDrM5XI5pqen2b9/P4ODg4RCoaJ2wN4MLly4wC9+8Qt0Oh2VlZU8//zz9PT0FH2LEUE2myUYDPJP//RPbN68mU984hOUl5fjdDrlzZvfgkU4msUYZrVaLa0jMXL50KFDRVF2ISx0o9G4bJ6ZGCckfFSi0ZjwY8ViMSYnJ/H5fJw+fZqFhQVGR0c5fPjwsu6XpcqaESDhtEsmkwQCAaLRKKOjo5w8eZL5+fnLBhSuRaanpzlw4ADr168nGo3yb//2b0XTYnUliOZqL7zwAnNzc2zevBm4GNk0mUxyuyLakYphlCITOJFIkEqliMViHD16lL6+PgYGBooi4CCymY1Go9xabd26FZvNhtlslmkDokg6lUoRj8cJBoMMDQ0xNjbGSy+9xOTkJAMDA3LLVuqockX4aLyeESkWi4Wqqiq6urqoq6tjZGSExcVFmXq/mhm/K/07N3sUjDDtxWz0qakp2fP5VnAr12mxWKisrMThcOByufjSl75Ec3MzdXV1suQkFAoRCoV4/fXXOXfuHPv27SOZTMrulrFY7KY0Z78Z61Sr1VitVhwOB11dXXg8HpxOJ5WVlWzfvh2r1SoHMPh8Pl544QUuXLgg+/skEgmCwSDJZJJ4PH5LruVCSMGasYBEi4mpqSlisRhjY2Mydb3YMn5vFalUinA4zOLiYsk/HUWPG+GUPXbsGIFAgLm5OWkFhcNhgsEgPT09DA4Ocvz4cVKpVNFutUWQYHZ2lkgkwsTEBPPz82i1WiwWCyaTCbPZjM/n48SJE4yMjDA4OLimr981YwGJ6IJw1gmLpxDLK5QFtNqs5jpFS9VLP0tswcT/3gpu5jov7XQortv8/87fVq7m9VuIe2XNCJD4vfwq4UKhCNBylHWWBsoW7AYpxv49CgoKV2fNlWIoKCiUDooAKSgoFIyi9AEpKCi8P1AsIAUFhYKhCJCCgkLBUARIQUGhYCgCpKCgUDAUAVJQUCgYigApKCgUDEWAFBQUCoYiQAoKCgWjKGvBSrWo71oLYYtpnaJfjdFoxG63y1HPor2FmMAZCoXkca+0ve2tWqf43FudS6sUo946ilKASgnRPqHU0Wg0VFdXU1FRwbp162SvYtFz5+zZs8zNzRXVaB/R/SD/eNbCuXg/oQjQTUA8+Ur1CWi32/F4PHzhC1+gsrKS8vJyNBoNarVazpYXTf+TySShUKigbU5Fb2iv14vBYCCTyciOgaJVqSJEpYEiQDdAfv8hccGXogg5HA7q6up46KGHqKiowGQyyTa2oVCIubk5RkZGiEQizM7OkkwmC2YFib7JBoOB8vJybDYbsViMUCgkx/Ss5Q6CsHasblAE6IbI7z+U35GxVNBoNOj1ej7/+c9z2223UVFRIf0+58+fZ3R0lFdeeYXZ2VlmZmZYWlpicXGRbDaLTqcryPHa7Xa2bdvGHXfcQXl5OQC/+tWvGBsbY3x8fE1aP+JBJyaBuN1u/H6/nPRSyn2wFAG6SYiLoFQESKvVUllZSUNDAxs2bKCtrQ2NRsPS0hKjo6OcO3eOkZERent7WVxcJB6PE4/HicViBTlelUqFxWJh/fr1bNq0ia1bt2IymYhEIqRSKTnWppRvxksRwmO327FYLNTV1WG1WikrKyMQCEgBymazZLNZFhcXmZ6elq+VBLkiBCjpn2Jfp1arzZWXl+f+9E//NOfz+XKJRCKXSqVy8/PzuZ/85Ce51tbWXFlZWU6v1+c0Gk1OrVbLH5VKldNoNDmNRrOq69RqtbnNmzfn+vr6crOzs7lUKpWbnJzMHThwIFdXV5fT6XRr7nzqdLqcxWLJffjDH879yZ/8SW5sbCwXDAZzsVhM/kSj0VwoFMr5fL7cN77xjVx9fX3OZDLd0nXeTN63FpBarUar1aLX69FqtbIReCmMML4RdDodVVVV/M7v/A633XYbVqsVjUZDIpHg6NGjnDx5ksXFRaLR6FUdzav9dFWpVLjdbsrLyykrK8NqtaJWq+nv76e3t5dIJFLyU0Dyp59qNBqMRiM2mw2n00kmk2FmZoZ9+/bR2NjIjh070Gq1spl9LpcjnU6zZcsWPvvZz/Lyyy8zPDzMwsJC0VtC70sBEo5Ms9ksw81isN1aH+NjMploamriz//8z7Hb7dKXE4/H+dWvfkVvby9+v/9dP2O1vxuVSkV5eTnV1dU4nU45I/2tt97ijTfeIBKJFP2N9l4I8TEYDOj1etxuNxUVFdTV1TE9Pc3g4CA+n4+dO3fS1dWFxWKRAiSmru7du5edO3fKbanf7y/67+V9JUB6vR6Hw8Hv//7vU1NTQ2trq0y4y2azxGIxRkdHee2113j++efXlAip1WqMRiN//ud/zubNm7Hb7XIKJ0AikeDAgQOMjIwU7iCvgk6n47HHHmPr1q3odDrS6TSJRIJz587R19dXEnPv3w2VSoXVasVsNuNwOKSzOZlMyvyrWCzGyMgIw8PDHD58mEcffZQ777yTqqoq9Ho9cPEc63Q6PvOZz7Bnzx6+8IUvsLi4WODVvTtrXoDEzHiLxYLFYsHj8bB3716am5tZv349Go0GjUZDJpMhHo8zNjZGIBDg4MGD+P1+EolEoZdwwwhHptvtZu/evXR3d8uLFi6KTzgcZnJykvn5+QIe6eUIa7Wrq4vOzk7UajXBYJCZmRlmZmZYWFgo9CHeFDQajZwdr9Pp0Gg0RCIRAoEAfr9fTkOdm5tjcHCQtrY2mpqacLvdy86lSqVi/fr1OJ3OZa8XLQXxPL0HXMFBplKpciqVKqdWq3NarVY6SMXrV/odvV6fq62tzf2X//Jfcm+99VZucHAwNzU1lYtEIrlEIpHLZrO5bDaby+VyuWw2m8tkMrlkMpkbGRnJvfbaa7m9e/euutNSrOdqa7rWH61Wm7Pb7bkvfelLuV/+8pc5n8+XS6fTy47jwIEDuW9/+9s5l8tVdM5Zg8GQ83q9uTfffDMXDAZzyWQy9+STT+bq6uqu29kqvmeNRpPT6XQ5vV4vHeyFWqc4FoPBIH90Op28xi99f01NTW737t25U6dO5TKZzGXHMj4+nquurr6m66gQlIwFlMsLcYunoslkQqPRYDab0ev1mM1muaUymUwYjUaqq6vZuXMnTU1NOBwO+VTI5XIkEgmZ8Zv/43K5AKSzs9j30e+G0WikvLyc+vp6Wlpa5HcGEAqF8Pl8HDt2jN7e3oJmN1+Nuro6WltbcTqdpFIpzp49y7lz55ienr5mx7M4v3q9Ho1Gg1arJZPJyJ9cAbfcIpQueK9jMZlM2O32ZVNVS5GSESB456RoNBoMBgMVFRU4HA6amprweDw0NjZSXl6Oy+Wirq4Om81GZWUlOp0OnU4nc0RSqRTJZJJIJCKFSjhjxX7caDRisVjQ6XSrug27mTeBWq3G4XCwYcMGOjo6aGlpQa1+pwHC+Pg4hw8f5rvf/S4nTpy4aX/3ZnLXXXfx0EMPUV1djd/v51/+5V84fvz4dc1/1+v10sGr1WoxGo0Eg0EikQjJZLKgOUTX+nfXrVvH7bffjt1uv2ruWSHXs1JKSoDgnS81m81itVqpqKjg7rvvllESo9GIwWAgnU4TCoUYHx9nfHycoaEhGR3IT9TavXs33d3drFu3DrPZDCBri8R7S438C1Kn0+HxeDCbzcvKRpLJJP39/Xz/+99nYmKiUIf6rqjVaiorK+ns7ESv1xOJRDh+/Pg1H69er8doNLJr1y5qa2tpb28nHo8zOTlJX18fw8PDwM0V/1uFyLh/t6z7QCBQEiF4KEEBgnfMVYPBgNPpZMuWLVRUVFBeXk4mkyGdTjMyMoLf76e/v58jR47w+uuv4/P5iMfjZDIZaUXlcjmcTifNzc1SgFKplBSrUsovuVJRrMFgoKysDKPRKF/LZDIEg0HOnTvHr3/961U/zpUgwtJlZWXU1dUBF1MFhoaGCIVC1/RZBoMBh8PB1q1b2bhxI5s3b5Zbz+npaRn5KxUB0mq1MoftUhHK5XLLSmaKnZIUIBGxmp+fx2KxkMvlUKvV5HI5zp49y9DQEP/8z//M2NgYkUhE9rHJt3zEZ9TU1LB161YsFov8/GPHjvGzn/2MoaGhQi3xuhA3kPCXqVQqamtrefTRR6mtrZUX6/DwMH/8x3/M4OBgIQ/3XRE5MeK8iid+MplcsVWqUqnQ6/WsX7+eD33oQ3zkIx+hubkZk8mE2WwmkUhw5MgRUqlUSdyscNGn5/V62bVrFw8++CBOp1P+m3j4Hjt2jBMnTpREBLckBUhswaLRKMFgEL/fj06nIxaLcebMGXp7ezl16hQzMzNXtWDEVs5kMuF0OpdllS4sLNDX10cwGFzNZd10hIO+pqYGq9UKXLQew+HwihIOC42o+hbn+1pFQlhRTqeThoYGvF6vvGG1Wq3M/yqVbXZ+8MXlcuHxeJblcgm/5oULFxgcHCyJdZW0AAUCAVQqFa+99hp6vZ5gMMibb75Jb28vqVRqRSa1qAjP72Y4MTHB/v37V9zxr1gRkRK32y2dz8IaXFhYKFhh6UoQwQIRMBBRS5EjsxIxEgJktVqprKyU21C1Wk06nWZ2dpZgMCiz34uR/C2WsArdbjdGoxG1Wr3sul1YWGBoaIhf/OIXvP322yVx/ZakAAlEv5ojR46g0WiIxWJMTU2tKJwsnHmipkalUhGNRjl79ixjY2OyurpUMRgM7Nixg3Xr1skLNZ1O8+KLL3Ls2LGifzqK8oJ8Z6uwAPIjee+GeFCl02lSqZT8/VwuRygUor+/n4WFhYKH4PMRaxU1YTqdTh6fTqfDbrdTXV0ty2iElRiPxxkYGOCFF15gbGxMinaxU7ICJCI5qVSKffv2yWLSlX7pIm09v6gvFApx4MABhoaGiv4GfS+MRiP33HMPmzdvlhd1KpXiqaeeuu4w9mqSn68jjl/ckFqtdkX+jdz/K9JMpVLE43F5ztPpNH6/n7fffpupqamietAI351ouiZKMnK5HAaDAZfLRWNjI263G4PBAEA6nSYSiXDs2DG+/e1vl1Q7jpIVIHjHj5PvfF0p3d3dfPGLX+S2226Tr83Pz/P0008zOTl50491NfF4PNTW1nLnnXdSX18vX8/lcgSDQYLBYEk8HeEd0YnFYhiNRvbu3cu5c+c4ffr0sv4/V1qP8IHV19eza9euZQ7bYDDIqVOnCAQCq7eY90A4zXU6nUyuNZlM1NTU4HQ6qampobGxkTvuuGPZeZ2cnOQrX/mKfLCUivhAiQuQ4FpvJtGS4q677pJd9cRT5PTp00XtG3k3RM1bfX09TU1NNDQ04PF4lr0nkUiURHREkN/21mQy0dnZSTqdZmlpSfZ/TiQSpNNpmWKRzWblzez1eqmoqKCqqkr6gEQEdHFxsagKWfNzfIT4CAGqqqqivb2d+vp6Ojo6pPWztLTExMQEb775JjMzMyUlPrBGBOha0Ov1dHZ2sn79ehobG6VPYGpqisnJyZJtxaHRaLjnnnt4/PHHaW1txe124/V6l6XqC39IKeQ2CQeyqHw3m800Nzfzh3/4hySTSRKJBH6/n2AwSH9/P4ODg/z617/G5/MRDAbRarU0NjbyZ3/2Z3R1dWE2m+XnTU5OMjc3V9De1lcim83KHDXhPK+oqGDjxo20trayY8cO2T5GrVaTSCT4xje+wfHjxxkcHCwqMV0pa1aARKp9bW2tTNwSlfFbtmyhu7tbOvHS6TRHjx7l6NGjJXFzXorZbKa1tZWuri7a2tpk2D3ff1IKafn55PtvkskkRqMRrVaL0+mUzmWbzUY0GgWQ2yufz0c4HEaj0VBVVUVbWxsej0ee53A4zFtvvUV/f39Rfh8ih8tkMlFWVkZDQwN1dXXS8WwwGFCpVMzMzDA7O8upU6cYGhoqqVymfNakAIkTWFNTw2OPPSZ7rZjNZqxWK7t378ZqtcqbM5lM8s1vfpPjx4+X5FPE4/Hw6U9/mu3bt8uWFZdmyIqCy1JBbJMikQjhcBir1SofJAKxDamtrSWTyfCxj32MWCwmw886nU7meIl+TzMzM3zlK19hYmKiKAUom82i0WjweDy0t7eze/dutm7dSmVlpczUz2azHD16lAMHDvDGG28wMzNT4KO+ftacAIl9dENDA21tbezYsQOHwyEvYJ1Oh9VqldGQZDLJ0tISoVCISCRS6MO/Lvx+Pz/72c/I5XJ0dXVhMBhkFEVsZURYt1QQTdg9Hg8mk+mKdU+XZn7rdDrUajUmkwl4p+3u3NwcExMTvPbaa5w9e5bp6WlpORUb2WxWzjxrampi69ateDweeS5FfpTI5yqlh8qVWJMCJE5gXV0dHR0duFwu7Hb7siee8IeEQiEWFxcJh8Ml5ZzNR6QPNDU1MTs7i9VqlfVP4qYUAiSso2J8+udjMpmor6/H5XJhMBjIZrMkk8llN5zYcoibVhSd5ucJZbNZfD4f/f39PP/88/T29sr5YcWIcKA7HA6qqqpobW1dtpUWGeHpdFqO5CllSk6AxMUlRvJeegJEPtDp06dlvxfxHlFXJMzxubk5fvjDH/Lqq68yNja26mu5mWQyGX7+859z5MgR9Ho9LpeLJ554QjovRTSpqqqKmZkZpqeni/riraqq4sEHH5Tjgg4dOsT58+f58Y9/TDgclh0C4aK/b8eOHfzxH/8xZWVl2O124B0/0qFDh/jqV7/K1NTUst8rRoQ1J/pWxeNx9Hr9suveaDRy9913s379eg4cOMDi4mJRr+ndKCkBEk8B4VAWAiREJr9pmQg35z/18z9DhN2npqY4f/58yVo/+SwuLrK4uIhWq8XlcjE+Po7b7Zb/Llqz2u12pqenC3ik747octDe3o7D4SCbzXL27Fn6+vo4fvw4kUhkmRWj1Wpxu90kEollFlImk2FpaUlOdi0FR63YSrrdbsxmM9lsVuZt6XQ62XhPJCK2tLQQCoWK1qf1XpSUAME7yWXiwsxms7J1Rjwel096m82Gw+HA6XRKn4BArVbLi1O09SiVrclKEDkxo6OjVFVVydfVajUNDQ0sLi4yODhYlP4DEb3q7OzkQx/6kJz5/r3vfY/e3l7C4fBl5yiZTMoq+fx/i0Qi9PT0MDIyUjIPGBHpu+OOO6itrQWQwyFramrwer20trbKLPE/+IM/4NixY/zVX/1VUXa0fC9KSoDE9kmE01taWmTzbRFiFT18RAfAfPNVfIYQq1AohFqtxm63L6uKTiaTxONxotFo0ZcsXA1hGV4qMmaz+TJBLiYMBgO33XYbGzduRKPRkEwmZYDgatsng8GA2WyW10Iul2NxcZHR0VF++tOf0tvbW4CVXB9GoxGj0Ug2m2VycpKRkRH279/P9PQ0TqeTzs5O3G43NpsNvV5PQ0MDCwsLJTOR91JKSoDgnTCl0Whk9+7ddHZ2Ul9fL+t7QqEQiUSCPXv2yKrh/FwYMf8rGo0SCATQaDS4XC4cDgdw0QQOhUL4/X5mZmZKVoAAmRUsUKlUMh2hWC9Yk8nERz7yEdatWycLhAOBAPF4/IopEiLqZbVa8Xg8ssXG1NQUvb29fPe73y0Z60ecH6PRSDKZZGJigv7+fl599VVGR0eBiy1qb7vtNnkPNDc34/P5ivZ8vhclJ0Cinklsv8xmM7W1tbJqWLThcLlc0pEn3vv6668zNDTEG2+8gd/vZ3FxUYqW6JBYXl4ufSWBQOCaGmAVC/ltKETXR+G0P3/+PMPDw0XtC7l0GzU/P086nb5si+xwOKioqOB//I//QUdHh+z7HY/H+cd//MeSy+sSBdaTk5N85zvfIRAIyIRDcb4uXLjA008/zcMPP8xtt922bJpqKboQSk6AAGmWB4NBotHosgby+e9JJpPMzc3J7VVvby+9vb288sor0m8kECHc/Azi/DqkUkLkv4inKbyTCS0c1aVyoYrjNpvNWCwWMpkMOp1ODiWoq6vjrrvuwuv1olKpCAQCzM3NcfjwYU6dOlXow79mUqkUwWCQkydPyoZ7+ZHcSCTC0NCQbJYnrlERbClGv967UZICJHJCfvCDH7B//36am5upqanB7XajUqnIZDKcPHmSU6dO8fWvf13m+MRiMen/udQCiMfjckDfpTkXpYbFYsHtdtPe3i4dmSIkPTs7y9zcXFELkPDZ5XI5amtrsdvtfPjDH2Z0dJRwOEx3dzd79+6VNW/ivCcSCb7+9a/zzDPPMDs7W+BVXB+ihfDS0pJ0GeRjsVhob2+XpSfCcne73bLPUSlRkgIE7zTfnpyc5I033qCiogKPx0M8HpcjbS9cuMDY2NhV/QdX+sxLt1ulaAHp9Xo5BdbhcCxrbVrs1fBihLQos9DpdFgsFjZt2kR1dTWxWIyWlhba2tqorq6Wvbynp6c5fPgwvb291zUzrFh4t5o9kaDY2dkpZ9fBxcDCpk2bOHv2LGfOnFmtQ70plKwAAbID4t/8zd/Ip/7c3JwcqXwzrJdithSuhHBkOhwOWlpaqK6ulv8m/CPFLkAulwubzSZzYrRaLb/9278NvOPfEkmlcDHt4MiRI3z2s58lFouVrPi8FxqNhurqah566CHZ4xvA6/Xy2c9+lp/+9KeKAK02uVyOSCQiI1vRaLTo2iysJrlcjkAgwNTUFAcOHKC9vZ0tW7YwPT3N5ORk0dZACaLRKP/+7//O1q1b+U//6T+h1+uXtWEVFmkmk2Fubo75+Xn+7d/+jf7+/jUtPkKY87O8BSIhcd26dXR3dzM2NkYoFCqJh+eaECBR/RwOhwt8NDeP/NSBa0X4sXp6ekin09TX1zM8PMzg4GDRN1uLx+Ps27ePVCrFBz/4QSwWi2zFIURI9M0RWexPPfUUCwsLJRXxulbUajUWiwW9Xk8sFpOBEtHArKamhqamJtra2vD7/UQikZIQY1WuCGWyFP0u+az0K72V69RoNDKd3+FwSN/PSpv2r4RbsU5R6ySacYnEvKamJrRarRylLFrLRqNRxsfHb2lhZjGcT7jo27PZbNTU1NDZ2UlzczP3338/lZWVVFZWMjMzw4ULF/inf/onjh8/ztTU1DWJUCGkoOQtIIUrk8lkmJ+fB94J1YqOgMVMLpcjFosRi8VYWFiQ9U+BQGCZAImE01J4yt8sksmkTKNIJBIsLS3h8XioqqqiurpaRs9WOpKqGFAsoFtAsTwxbzWruU4hotczgOBGKcbzeWkCYn65kShHutbvSLGAFBSuQqm1lL3VXK3Wr9SyoVc24U1BQaEkKCXxAUWAFBQUCogiQAoKCgWjKJ3QCgoK7w8UC0hBQaFgKAKkoKBQMBQBUlBQKBiKACkoKBQMRYAUFBQKhiJACgoKBUMRIAUFhYKhCJCCgkLBUARIQUGhYBRlNfxqtzXI52Ykhq/0MzQazYqrvPN7IYvugGq1Wk74KERfnGJsU3GzEfPUVvre6/0bAjHD7dJ/W8l1Iq4Jm82GRqMhHA7LWXkrQWnHscrkz/4STc7FjbwaJ+Na+laLC1D85M8sU6ppbh238rvNv/bE3xJ/L//azG++/25otVoMBgMNDQ1YrVbOnTsnx4sX6zXyvhUgMdq2s7OTxsZGTCYTqVSKiYkJZmZmGB0dvWy0caERc6IymUzJ9X1RuByVSoXJZKKsrAyr1YrJZCIUCpFOp0kmk2i1WvR6vRyyKSbEXnrexfSQ5uZmuru72bZtG2azmR/84AdMT08TiUQKtML35n0vQG1tbezcuROHw0E8Hqe3txeAycnJohIfeOdpnL/lutRkVygt9Ho9LpeLqqoqXC4X8/PzxONxwuEwBoMBk8lEPB4nHo/Lab753Q6z2aycpVZVVcXWrVvZs2cPRqORl156SU5QLVbetwIkTN9QKCQH2cViMWZnZ4lGo2i12qKcsiC2iWLctHhNofTIZrPymuvo6KCrq4tIJEI8Hsfv98sR1OvWrcPtdpNKpUin08RiMQKBAEtLS5w5c4ZYLIZeryeXy/H666/zi1/8gkgkwsjICPF4vKivj/etAIkb2efzMT4+TjQaJZFIMD8/TzAYLDrr51Iu9RUIH1axH7fCctLptJwB7/P55BRfEVwQlrrdbqeyshKVSkUymcTv9xMMBrFYLCwtLREIBJiZmWFycpLZ2VkpZMUsPlCk/YBWY0uRf+PmO3Oz2ewN9x9ejeiQOH4REdNoNGQyGdLp9HU1JL8ebvY6xfuEmBZLH+jVOJ8ajUZei2Lel8PhoKysjC1bttDS0sLnP/95nE4nRqNRfjfZbJbp6Wmefvpp3nrrLV599dXrfggpUbBVRHzZq3Wz3mycTid2u52amhqsViter5doNEo4HGZwcBCfz1cy0zHzyZ/2oNPpcDqdmM1mAoEAyWSSeDxOOp2+ocjOpWHvYkA0mBfHptFoCIVCZLNZTp8+zdzcHHq9nu7ubh566KHLfndoaIjZ2dmSs4DflwIkIkjFcvFdD16vl4aGBvbs2UNVVRVdXV0EAgGmp6d5/vnnOXPmjAzBlhpqtRqDwSDn21dWVnL+/Hm5TYnFYkSjUWmtXisajQZYbvEWC/kh93A4TDgcZnZ2FpVKxYEDB3jooYf46Ec/ukxEo9EoJ0+eZHp6ulCHfd28bwRITNzUaDQkEonrTt67NP9mtS/esrIy1q9fz4MPPsiePXvweDyYTCYsFgvpdJpEIkFjYyNzc3OcPXuW06dP8/zzzxfVTXY18o+xrKyMXbt2sWfPHrq6uqRfZGJigv7+fg4ePMjIyMiKozwqlYqKigo8Hg+//du/jdPpxGaz8cILL/DWW2/h9/uLWqzFwMYrTbVNpVJMT08XfcTrSrwvBEhEE5xOJ1qtlsXFRZLJ5HVnDxfKhFer1TidTtavX8+2bdvYtWsXWq32smxdi8VCOBymvLwco9HIkSNH5LYlEAgU9Y0m0Ov1lJeX09TURFdXF2azmVQqxeTkJACjo6PMzMy86zZTbOeMRiNms5n6+npqamq4/fbb8Xq9OJ1OxsbGGB8fJxKJFP33cqU5YHAxmhaJREgkEgU4qhtjzQuQSqWira2N7du3s3XrVkwmE08//TRTU1OMjIxc82fBO6b7aqJWq3E4HOzYsYO//du/xWKxoNfrl70nlUqRSCSwWCzYbDYqKyvZs2cPn/vc55icnGRiYoI/+7M/4/z580VrEeVyOVKpFIFAgLNnz7JlyxYymQwajQaDwUBTU5OM+oyNjbG4uHjFm9JgMMgcm7179/LAAw/Q1dVFeXk55eXl0nn/xBNP8MADD/C5z32OM2fOFGDFN0YxbiOvhTUtQGq1GpPJRH19Pbt376atrQ21Wk1DQwPJZPKaBUgk/RXiZBsMBu6880527tyJy+WSVs+5c+ek7yeVSpFMJjEYDBiNRjZt2oTNZqOqqgqdTofFYuHee++ltraWN998s2jnqudyOZLJJD6fTz7ZxbGK/Cexjb5a5ElECF0uF+Xl5dTW1lJVVUVZWRlGo1H+nt1ul4JU7ORHbOHid3HkyBGOHTtWtOfyvSj+b/0G0Gq1eDwedu/ezec//3my2SyhUIidO3cCcPTo0RV9TqFmkufjdDr5u7/7O+rq6uRFmEql+NGPfsTx48f55S9/KbcQarWasrIyvv71r7Nu3Tq2bduG1+vF6/XyjW98g6NHj3LXXXcRi8UKspb3IpfLEY1GGR8fl3lZFosFjUZDLBZjbm6OsbEx4vH4u36GXq+nrq6OmpoaKioqcDgcmEymZe8T23NxcxezJaHVauWWGyCZTPK1r32Nnp6eokyaXQlrVoC0Wi2VlZU8/vjj7NmzRzqPk8kkBw4cuKK5LZ6aHo+H6upqtFotmUyGmZkZIpEIfr+/ACsBj8dDTU0NFosFnU5HNpvl+eefZ9++fRw6dIjZ2dllYWkhtN/73vfo7OxkYWGBrq4u6uvr0Wg0WCwWWlpamJ2dZX5+viBrei8ymYxMDk0mkywtLZHJZJienpbC9G4+j3Q6TTAYpL+/n1AoxPnz53niiSfYsGEDBoNB3sQ+n4+xsTGSyWRRi4/VauVTn/oUu3btkq/lcjkWFxdZXFws6mN/N9acAAmhMZlMVFVV8ZGPfITq6mr5dEskEvT39zMxMXHF39Xr9VRUVNDd3Y3BYJBPloWFhYIKUG1trdw6RKNRfvOb3/DP//zPpFKpyy4+ETF59dVXGRsbw+l04nK5qK+vl9HAlpYW0ul0UQuQEJ9UKiXFaGpqirm5OZaWlq649vzfj8VijIyMMDMzw6lTp7jvvvtob2/HYDDI9+VvX4sZk8nERz7yEdrb2+VruVyOYDBIKBQq4JHdGGtKgFQqFWVlZXg8Hj71qU/R2dlJW1sbRqMRgNnZWUZHRwkGg5eZ7yqVCovFQkdHB/fffz+PPvooBoOBWCzGD37wA/r7+6/ZZ3Sz1vRf/+t/5e6778Zut3Ps2DG++tWvcvLkyXe9AQWjo6N85zvfob6+nh07dqBWq6mrq+Pv/u7vePrpp4vW8ZrL5Uin04RCIRYXF6XvRkQyRWHmSoIByWSSUChEMpmUDlvxQBoZGeHo0aNFXTEOFy36zs5Oampqlr1ebB0brpU1I0AiSlJRUUF9fT0dHR00NTVhMpnQaDSy8C8ajcrGTfkOPaPRiMPhkKLV0NCAwWAgHA5jt9uliK0mer0es9lMQ0MDLS0taDQa/H4/x48fZ2FhYUVmdzweZ2pqinPnztHb20t7ezsmk4nW1lba29vp6OhgcnKScDi8Ciu6NkRELJVKodPp0Ol0uFwuLBaL9IWs5DsQYiY+Kz9/SxR3FvtNrFarMZvNBbkObyVrRoDMZjM1NTXcfffd7Nixg+bmZhwOh8x/yWQyRCIRYrEYTqdT+hXgopVRU1NDV1cXf/RHf0RVVRVWq1XW5ESj0Xd1eN4qqqqqWLduHR6PR1bnh0Ih2avoWvjWt77FT37yE5577jm6u7vR6XTce++9NDY28pd/+Ze8/fbbt2gV14cIL4uEUZvNhtPpxOv1MjMzQ1VV1RW30Vf7LIBIJMLS0pKMIuZyOUwmEy6XqySiYJdS7KK5EkrvW78CIiQtQusqlYrz589jsViorq6mpqaGpqYmjEYjNTU1fPKTnyQUChGJRGSymtPppKqqisrKSqxW67IudaFQiGg0umrrUavVWCwWurq6ePjhh6muriabzTI3N4fP57uuCy8Wi7G0tCQTMEVeUWNjIxaL5Ras4uYgmnPlFw57PB46OzsZGBhgdnb2PT9DRLpsNht2u12KTyaTkfVlxXwzWywWHA6HvCbhomUrasVKmTUlQJFIhN7eXs6cOUMoFEKv19Pc3Mztt98uCza9Xi8bNmwgm82SSqXQarVyiybyhi7NtVhaWlpVH4HIX9m1axdPPPEEarWaZDLJ2NgYc3Nz1/WZopQhmUySTqfR6XTY7XYsFgtms7koQ9AiH0ikC4garqqqKrZt28ZvfvObFX2OTqfDZrNRVlaG2+2W10s6nZaNvor5RnY6nXg8nmUCFIlEWFxcLPrs7fdiTQiQuFADgQChUAiVSkU6nUatVhOJRJifn+fo0aPceeedtLa2snv3bsxmMxaLZVkvnfw6L4FGo8Hj8eBwOFZtPWazma1bt1JfXy8vung8zv79+2XHxutBPPXzuykWm+hcyuTkJL29vdx99904nU40Gg12u53GxkbsdrtsWXolRKvSvXv38vDDD9PW1gZcdNxOTEzw5ptv8utf/5ojR44UdR3V5z73Oe644w7sdjtw8bz9+Mc/5vnnn1/xNrRYWTMCdLU6mVgsRigUYnJyUvp+amtr8Xg8VFVVyT4scPV+LvnvWQ10Oh1lZWWYzWb5ZBb9qm8kbH6p2AgrsJhFKBAIMDk5STQalVneOp0Oh8OBzWbDbDbLSFD+OtRqtXRat7a2snfvXlwul9yqz8/Pc+LECQYGBmQeUDGiUqno7u5m165dsuthLpfj3Llz7Nu3ryTrv/JZEwL0Xohckp/+9Ke89NJL/Ou//it79+7lT//0T6mqqpJm+aXkcjni8ThHjhxheHh41Y43k8nI1hNzc3NYLBbi8bjMhbneaRhipI9wuAYCAaampgiHw0UrQiJtYmRkBLPZTFlZGblcDovFwpYtW8hmsxw6dIhYLLZMTK1WK9XV1Xzyk59k48aN1NfXy8EDJ0+e5NChQzz33HOyvUexrl+lUsne0GKbLB4ciUSiaI97pbwvBEg8NUQULB6PMzw8TG9vr/S3wDsWkJilNDg4yPDwMLOzs6ua7JVMJpmcnKSvrw+r1YrBYCAejzM5OUkgELguf43BYMBqtaLT6aQvRVgJl45/KSZEDs9bb73F1NQUbrdbnp+xsTEikQhGoxGbzYbX6wUunkebzUZFRQXNzc14vV7UarXsr3P06FH6+vrw+/1FfRPr9XpMJhM6nW5ZUGQ1u17eat4XAiQQW7VIJMK5c+f43ve+h8lkoqWlRVoFIos4FArx9NNPc+DAAS5cuLCqpm44HObQoUOcPHmSn/zkJ8vKLK7X6SiifKInUi6Xw2g04vF4MJvNaDSaonRoplIplpaW+NrXvia3XvDONAjRurS9vZ2HHnpIbpdtNhsWi4Wamhq5TZuammJsbIxvfetbzMzMFLXfBy5acVVVVTJIABcfjvF4vGSLTy/lfSVA+VitVtrb23G5XPLpItL3e3p6eO211zh48CCjo6MFuTGz2aysAs93Fl9P+wWVSsVdd93F/fffLxubw0Xfll6vx+12U15ezszMTNFGg8T3EAwGlzXkV6vVJBIJnE4nCwsLrFu3Tm63dDodZrOZaDTKxMQEr7zyCgMDA8zPzxdtIW4+O3fu5LHHHqO1tVW+dvbsWZ5++mkOHz5cwCO7eZScAN3oVkFERux2O01NTTgcjmVPl1gsxpkzZ/jZz37G8PAwS0tLBTF1hal9o+KnVqvR6/Xs2LGDRx55BLPZvOzftFotVqsVu93O3Nxc0QqQsF6vlI8Vi8Xw+Xz4fD6sVivNzc1yaymKUqenpzl06BDHjx+Xha3FTkdHB4899tgy/+T4+DjPPPNM0VtvK6VkBEiUT+h0OukDuFZh0Gq12O12PvOZz7Bx40buu+8+GdoU3QL37dtHT0+PHNVzK8XnVo9WVqlUrFu3jt/93d9l165d8qYUf1NkGUcikZIYRXQ1hNP+3Llz7NmzB51OJ5u1qVQqRkdHefHFFzl16pScAVcq5A+eFNsvn89XUmt4N0pKgMR2IZFISGfye1kIojJeOCkrKyvZunUrbW1tVFRULOutE4vFWFxcJBgMlkR90LshsrtramrYtGmTdMTmIxLxxHdZyohOBhqNRvqBhLAvLS1x/vx5AoFASYStRWBElAPBRfEZHx9nZmam6Cv3r4WSESBxUm677TaWlpaYn59neHiYQCBwVaEQW4zOzk727t3LJz/5SdatW4fVal2W25PNZllcXJS+AeHkK6bZWteK0Wjkgx/8ILt37+aDH/yg9InkEwqFZG+dpaWlkhZcl8vF7t27qa2tldaPsPImJibYv39/Sfh94GLA4KMf/SgbN26UAhQKhfjmN7/JyZMnb+izi20kUckIkHDE6vV6GhsbWbduHU1NTQSDQSkW+c5Zi8WC0WjE5XLJxuZ1dXUyFC1IJpMkEglOnDjB+Pg4fX19TE9Pr0qf3Vu59dJqtVRXV+P1ei+rHBfflc/nY2hoiHA4XNLio1KpsFqttLS0LMtYj0ajnD17lsnJSdnCtdjRarU4nU5uv/126XwOhULMzc3R19d3w/lot3rbf62UjAAJkdFoNLS2trJt2zbm5uaIRqPSHyQmg+ZyOaqqqnA4HLIqvqys7LJkw2w2SzweZ2lpif3793Pu3DkGBgYIBAIlnWchtqv19fVUVFQAyxvpi+9qbm6O3t5eAoFAUa31Wp/SGo0Gp9NJZ2cnbrdb/l4kEuHw4cOcP3++qLctYr0i6bCiooIHH3xQ+if9fj8TExMcPXqUhYWFm/K3ikWMS0qAgsEgPT09WCwW1q9fT2trq2xTKpLpxBcrUvZNJhN6vX5ZBfTCwgKnTp3iRz/6EYFAgGAwyPDwsExUS6VSJStAwhqwWCxMTU3JzOempiYqKipkjx2fz8exY8d48cUXr7vA9VYgfDkicTIYDBKJRK54LkR3x927d7N9+3Y8Ho8cWxyJRBgdHeV73/se4+PjBVjJuyN8k52dnTz66KM4nU5pnYueRyJf67vf/S779u27KcmwIgm1WJzYJSNAouB0ZmaG2dlZFhcXqampke1Gr1SvJZ76olA1FovJtp69vb28/PLLBAKBoq+GXikiUmi1WrHZbASDQWZnZzEajVKQVSoV8Xic8fFxLly4wPnz54vONyLyd8rLy+U5FUEBERUSyYZOp5Ouri6am5sxmUxotVpyuRzz8/OMj49z6tSpVW2lshKEb9Lr9dLa2spdd90lC541Go3cQosGej09Pbz99ts3xYF+I/PrbwWqXBE+5t9t1IpGo6GsrIyqqio+9rGP0d3dzb333ovZbF7WVErk0IjU+9dee419+/YxMTEh62iE7+NmfwUr/bybfTFYLBbsdju7du3C6/UyPj4u25Y2NzdTXV1NVVUVoVCIV155hdHRUYaHh69bfG/FOtVqNV6vl7a2Nh566CHZA3rfvn34/X4ymYwcNPjZz36WrVu3smvXLmw2Gw6HQ+Zy/dmf/RknTpzgyJEjN/y0v5nrFGUiXq+XP//zP6ejo4Pt27fLtjDwTkP+X/7yl3zve9+jp6fnplmp7+YDKoQUlIwFBO/4LsLhsGw0nk6nZUazw+GQvXsmJiYIh8MEAgHOnDnDiRMnGBkZYX5+fk1YO/mI5EqbzUZ5eTl6vV6KbzKZJJlMMjs7K7+7SCTC5ORkwZIs3wtxk7a2tlJWViY7V4qiWZPJhNVqZdu2bbS1tVFWViYrxSORCD6fj9HRUSYmJorqXAs3gcViweVy0djYSFVVFXq9XjZby2QyhEIhDh06RE9PD0NDQze1F1Wxne+SEiB4Z2ZULBbjlVde4fjx43i9XhoaGujo6KCvr4/BwUGee+45pqammJmZKYm+NzeCRqOR1d8dHR2k02kWFxfx+/3SApqenpZjmcPhsIwMFeP3ks1mcTgc7Ny5U04wfeSRR8hms3LAokilyO/nJNY5NDTE4OAgk5OTRbU+sbUqKyujrq6OlpYWysvLpeUjHrDj4+N8+ctfZnx8/Kb7r5Qo2E1AfHnxeJyFhQWef/557HY7drtdjs8ZGxsr+fDy1RBPUuGwtVqtdHR0yHnnExMT+P1+6VAXCYeir7TYghaLIzIfYcWEw2GCwSBut3tZM/ZLW4rkcjnC4TAjIyO88sorDA0Nyb5JxXKTCcTNL/xa4XBYBlF8Ph+Li4s899xznD17VgZFbjbF9p2UpADBO07pVCrFW2+9JZ8epTwneyUIR7OoBDebzTLdQFgGooWFSFFIpVLSjBcWUbFG+UQPpnA4LGu78ieCivMrWstms1mCwSBnz57lxz/+sZwDVmzk+4fE/w+Hw1itVsxmM7Ozs1y4cIFnn3226NMGbiYlK0DwTnKi6GZXjDfUzUSEbr1eL+Xl5bjdbjwej+wXIyKBYvqDaNKVX66SnwtUrGQyGXp7e/nTP/1TbrvtNjZs2EBHRwe5XI4zZ84wMTHByMiILBZOJpNEo1FmZ2eLttQiv4JfROrOnTvH/Pw8LpeLH/3oR/zmN78pWPeFQlHSAiQo5pvpVpC/XtGcKhaLYTAYCIVCspZN5DOVolUYCoU4d+6cHK0kttMis/nChQuMjIyUVBFtfmO8QCDA2bNnsdlsWK1WBgYGOH/+/PtKfKDEwvClwq0Mw4tUBNHZUGxD8v+2mKdVLKUkN3I+hVWXn8ErbuTVEp6bvU6xJlESJFqsFtonVwgpUAToFnCrb0whQiJsm//3VvN0FirfabW5FevMn8BSLFFaJQ9IYUWIZmUKpUuxiE6hWb1ZMwoKCgqXoAiQgoJCwShKH5CCgsL7A8UCUlBQKBiKACkoKBQMRYAUFBQKhiJACgoKBUMRIAUFhYKhCJCCgkLBUARIQUGhYCgCpKCgUDAUAVJQUCgYigApKCgUDEWAFBQUCoYiQAoKCgVDESAFBYWCoQiQgoJCwVAESEFBoWAoAqSgoFAwFAFSUFAoGIoAKSgoFAxFgBQUFAqGIkAKCgoFQxEgBQWFgqEIkIKCQsFQBEhBQaFgKAKkoKBQMBQBUlBQKBiKACkoKBQMRYAUFBQKhiJACgoKBUMRIAUFhYKhCJCCgkLBUARIQUGhYCgCpKCgUDAUAVJQUCgYigApKCgUDEWAFBQUCsb/D2Kas75WFU70AAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"execution_count": 1,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"display_image(EPOCHS)"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "NywiH3nL8guF"
},
"source": [
"`imageio`로 훈련 중에 저장된 이미지를 사용해 GIF 애니메이션을 만듭니다."
]
},
{
"cell_type": "code",
"execution_count": 28,
"metadata": {
"execution": {
"iopub.execute_input": "2020-09-23T06:52:40.916183Z",
"iopub.status.busy": "2020-09-23T06:52:40.915457Z",
"iopub.status.idle": "2020-09-23T06:52:41.080194Z",
"shell.execute_reply": "2020-09-23T06:52:41.080664Z"
},
"id": "IGKQgENQ8lEI"
},
"outputs": [],
"source": [
"anim_file = 'dcgan.gif'\n",
"\n",
"with imageio.get_writer(anim_file, mode='I') as writer:\n",
" filenames = glob.glob('image*.png')\n",
" filenames = sorted(filenames)\n",
" last = -1\n",
" for i,filename in enumerate(filenames):\n",
" frame = 2*(i**0.5)\n",
" if round(frame) > round(last):\n",
" last = frame\n",
" else:\n",
" continue\n",
" image = imageio.imread(filename)\n",
" writer.append_data(image)\n",
" image = imageio.imread(filename)\n",
" writer.append_data(image)\n",
"\n",
"import IPython\n",
"if IPython.version_info > (6,2,0,''):\n",
" display.Image(filename=anim_file)"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "cGhC3-fMWSwl"
},
"source": [
"코랩에서 작업하고 있다면, 아래의 코드에서 애니메이션을 다운로드 받을 수 있습니다: "
]
},
{
"cell_type": "code",
"execution_count": 29,
"metadata": {
"execution": {
"iopub.execute_input": "2020-09-23T06:52:41.085319Z",
"iopub.status.busy": "2020-09-23T06:52:41.084710Z",
"iopub.status.idle": "2020-09-23T06:52:41.086970Z",
"shell.execute_reply": "2020-09-23T06:52:41.086498Z"
},
"id": "uV0yiKpzNP1b"
},
"outputs": [],
"source": [
"try:\n",
" from google.colab import files\n",
"except ImportError:\n",
" pass\n",
"else:\n",
" files.download(anim_file)"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "k6qC-SbjK0yW"
},
"source": [
"## 다음 단계"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "xjjkT9KAK6H7"
},
"source": [
"이 튜토리얼은 생성적 적대 신경망을 만들고 훈련하기에 필요한 코드를 보여줍니다. 다음 단계로, 다른 데이터셋을 이용하여 실험해보고 싶을 수도 있습니다. 예를 들면 [캐글에 올라온](https://www.kaggle.com/jessicali9530/celeba-dataset) 대규모 연예인 얼굴 데이터셋 (Large-scale Celeb Faces Attributes (CelebA))이 있습니다. 생성적 적대 신경망에 대해 더 배우기 원한다면, [NIPS 2016 튜토리얼: 생성적 적대 신경망](https://arxiv.org/abs/1701.00160)을 추천합니다."
]
}
],
"metadata": {
"accelerator": "GPU",
"colab": {
"collapsed_sections": [],
"name": "dcgan.ipynb",
"toc_visible": true
},
"kernelspec": {
"display_name": "Python 3",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.9"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
 \n",
" TensorFlow.org에서 보기\n",
"
\n",
" TensorFlow.org에서 보기\n",
"  \n",
" 구글 코랩(Colab)에서 실행하기\n",
"
\n",
" 구글 코랩(Colab)에서 실행하기\n",
"  \n",
" 깃허브(GitHub)소스 보기\n",
"
\n",
" 깃허브(GitHub)소스 보기\n",
"  Download notebook\n",
"
Download notebook\n",
"  \n",
" TensorFlow.org에서 보기\n",
"
\n",
" TensorFlow.org에서 보기\n",
"  \n",
" 구글 코랩(Colab)에서 실행하기\n",
"
\n",
" 구글 코랩(Colab)에서 실행하기\n",
"  \n",
" 깃허브(GitHub)소스 보기\n",
"
\n",
" 깃허브(GitHub)소스 보기\n",
"  Download notebook\n",
"
Download notebook\n",
"