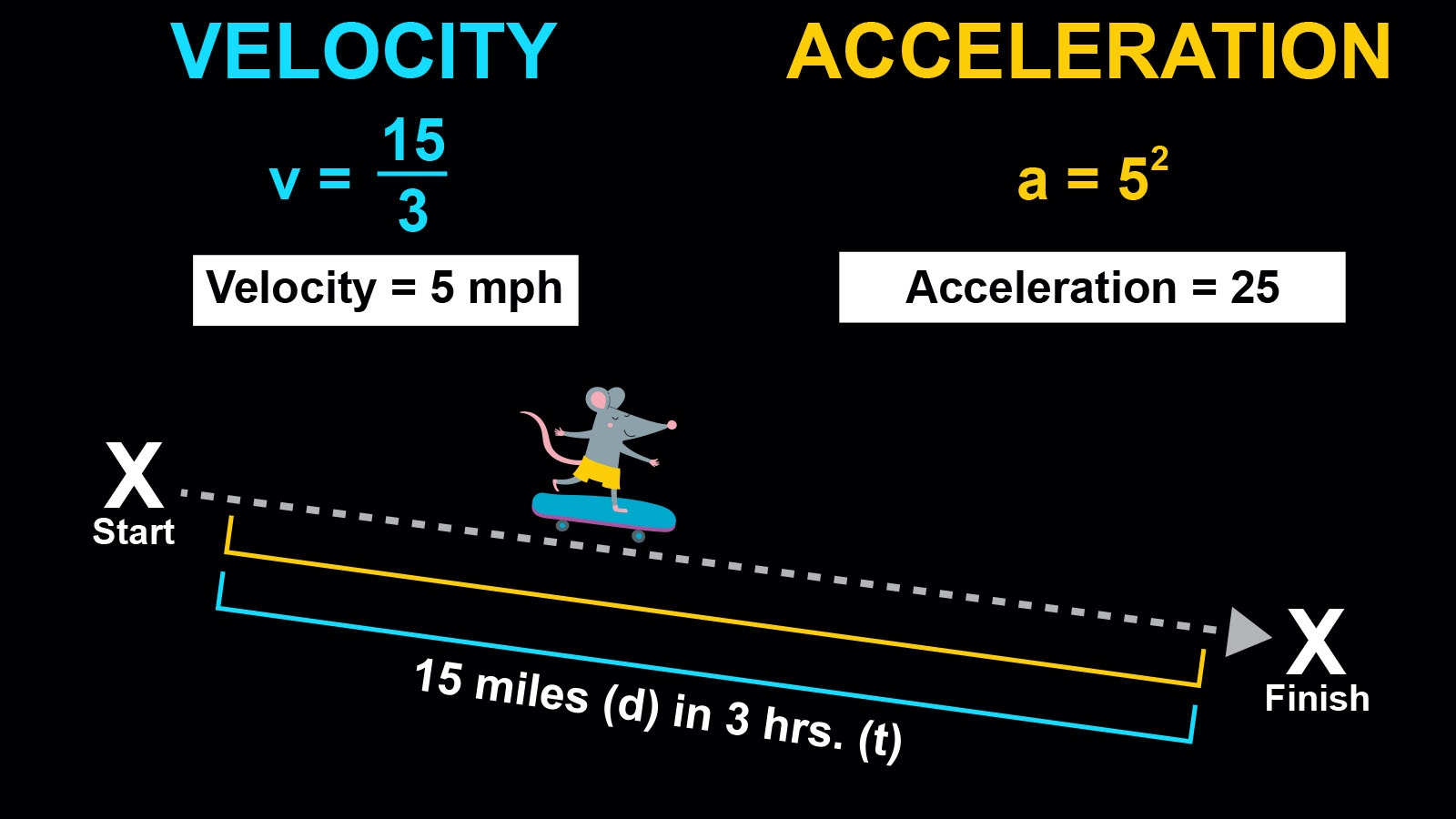
Relate Acceleration To Velocity Equation at Randy Llamas blog

Relate Acceleration To Velocity Equation. Acceleration, \(a\), is defined as a rate of change in velocity, resulting from a change in the magnitude and/or the direction of the velocity. The change in velocity can be calculated using the equation: The relationship between acceleration and velocity in this case can be described by the equation: By the end of this section, you will be able to: If acceleration a (t) is known, we can use integral calculus to derive expressions for velocity v (t) and position x (t). Integral calculus gives us a more complete formulation of kinematics. Define and distinguish between instantaneous acceleration, average acceleration, and deceleration. An external force is one acting on a system from. Useful equations related to acceleration, average velocity, final velocity and distance traveled. V = u + at v = u+ at.

Useful equations related to acceleration, average velocity, final velocity and distance traveled. The change in velocity can be calculated using the equation: By the end of this section, you will be able to: V = u + at v = u+ at. If acceleration a (t) is known, we can use integral calculus to derive expressions for velocity v (t) and position x (t). An external force is one acting on a system from. The relationship between acceleration and velocity in this case can be described by the equation: Define and distinguish between instantaneous acceleration, average acceleration, and deceleration. Acceleration, \(a\), is defined as a rate of change in velocity, resulting from a change in the magnitude and/or the direction of the velocity. Integral calculus gives us a more complete formulation of kinematics.

Difference Between Velocity and Acceleration Explained

Relate Acceleration To Velocity Equation Useful equations related to acceleration, average velocity, final velocity and distance traveled. V = u + at v = u+ at. The relationship between acceleration and velocity in this case can be described by the equation: If acceleration a (t) is known, we can use integral calculus to derive expressions for velocity v (t) and position x (t). Define and distinguish between instantaneous acceleration, average acceleration, and deceleration. An external force is one acting on a system from. By the end of this section, you will be able to: Useful equations related to acceleration, average velocity, final velocity and distance traveled. Acceleration, \(a\), is defined as a rate of change in velocity, resulting from a change in the magnitude and/or the direction of the velocity. Integral calculus gives us a more complete formulation of kinematics. The change in velocity can be calculated using the equation: